任務設計 抵達真實的學習

文|黃偉華 羅鳴亮

一般情況下，教師在進行教學設計時，考慮的是教學目標有什么要求、這節課要教什么知識、時間該怎么安排等，設計的是“教”。比如課堂中常呈現出用固定的視角提問題，或者教師說前半句，讓學生順著接后半句，顯得特別省力。但這樣的教往往解決的是知識技能目標的要求，而不是學生的學習訴求，更多是靠生搬硬套的外在標準來衡量，學習并未真正發生。長此以往，不管是教師，還是學生，都容易把自己困在認知的牢籠里，看問題的視角越來越狹隘，一旦遇到新的挑戰，就不知所措。

有教師認為讓學習真正發生，需要的是有效激勵，可以通過表揚、獎勵等方法來解決，但我們認為，這些只是外在的歸因。事實上，只考慮知識的“教”是不夠的，甚至可以說是本末倒置。更值得我們關注的是“學”的角度、影響“學”的內在因素。這就需要我們從根本上轉換視角，結合學生的學情、需求、興趣等因素進行“學”的設計，把一次次的學習設計成任務，用任務來激發學生的好奇心和探究欲，驅動學生打開多元的視角，主動創造各種可能的“學”。

怎樣設計學習任務呢？我們以為，要推動學生不斷地深入到學習的本質，可以從有意思、有價值、具有挑戰性等角度來思考，使學生獲得解決問題的能力，獲得學習的掌控感，增強內心的力量。

一、以趣啟智，讓任務有意思

課堂上，不難發現，許多學生沒辦法沉浸其中，他們有著自己的煩惱，即使是學習成績好的學生，有時對所講的內容早就了然于胸，但還是正襟危坐，積極舉手，認真操作，努力聽課，保持著好學生的形象。這樣的學習，很難體會到學習的樂趣，很難獲得更多的啟發和新的生長。怎么設計任務會讓學生覺得有意思，產生強烈的樂趣，從被動接受轉向主動參與？

比如蘇教版五年級下冊《因數與倍數》一課中，學習一個數的因數和倍數的特點（如下圖）時，課堂通常按著教材的安排，先找出幾個數各自的所有因數，再引導學生進行觀察，而后發現并歸納一個數的因數、一個數的倍數的基本特點。其思考含量不大，探究價值不高，很難打動學生，缺乏學習的動力。

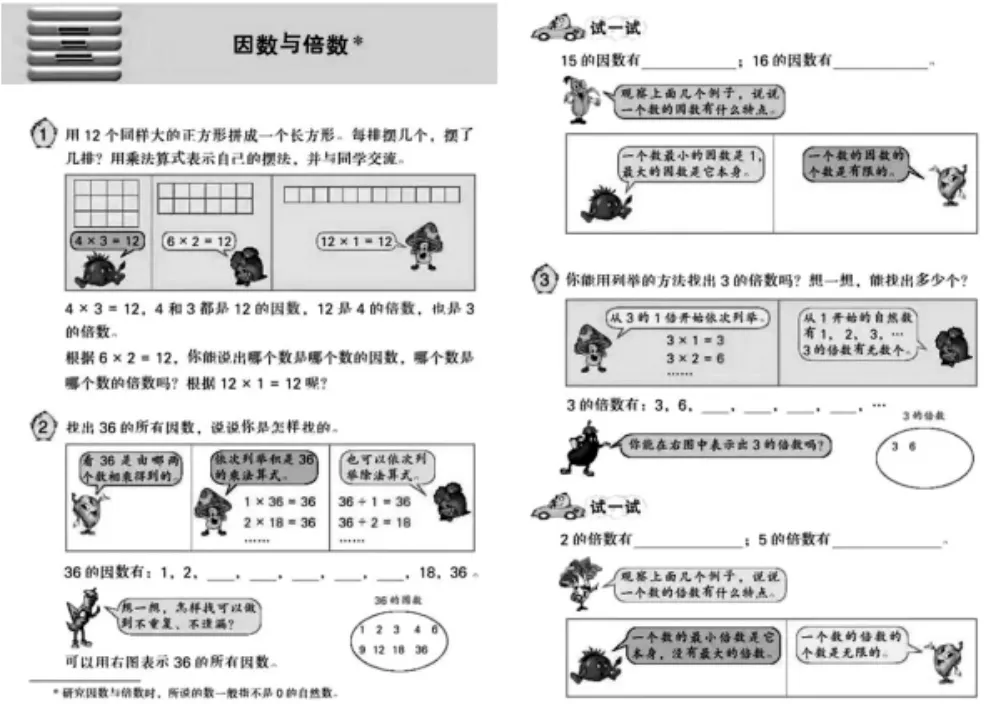
怎么把單調的活動變得有意思，變得好玩呢？林錦城老師執教這節課時，設計了猜數任務，就顯得很有意思。

師：老師帶來一張卡片，它的后面躲著一個數，想知道它是誰嗎？不告訴你！但可以給大家一個提示。

師：它的因數也是像這樣（手指36、15 的因數的板書）從小到大排列，有6 個因數。（貼6 張卡片）

師：你能確定它是誰了嗎?

生：（搖頭）不能。

師：給大家最后一個提示！這6 張卡片我只翻開一張！翻哪張呢？翻第一張？

（學生迫不及待喊：不行、不行）

猜數任務的設計，點燃了學生的好奇心，挖掘出學習內容里的智趣因素，學生想一探究竟的欲望油然而生。而“翻哪張”，瞬間勾起了學生的批判力，在教師說翻第一張時，脫口而出的“不行”，已將學生內在的思維活動暴露無遺，一只只高舉的小手，更讓我們讀到“我想說”“我來說”的渴求。

生1：第一張是1，翻開沒用。

師：我還沒有打開這卡片你們怎么就知道是1？

生2：所有自然數最小的因數就是1，翻開1 不能幫助我們判斷這個數是幾。

師：你是怎么知道的呀？

生2：從上面看出來的，36 的因數最小是1,15 也一樣。

師：（在相應板書中圈出1）果然是這樣！你們有善于觀察的數學眼光，這些數的最小因數都是1。

師：你們想翻開哪一張？為什么？

生3：最后一張。

生4：最大的那一張，就是它本身。

生5：從上面的學習可以看出，36 的最大因數是36，15 的最大因數是15，那這個數最大的因數就是它本身。

（教師翻開最后一張因數卡片28）

生：（齊）這個數是28。

以上學習，不需教師提要求，學生已經主動分析推理。不難發現，一個數的因數特點學生早已洞悉。在猜數任務中，學生不僅暴露了自己的認知，更是主動遷移運用，積極地投入到探究學習中。隨著“翻哪張”的說理，自主建構起只需要根據一個數的因數特點就可揭曉這個數是幾的認知。這一有意思的任務，符合學生的心理特征，把淺顯易懂的知識化為富有思維含量的任務，學生玩得有趣，又想得深刻，發展了心智和批判思維。

二、化終為始，讓任務有價值

日常學習中，我們常常順著學生的思維來教，由簡到難，循序漸進，一個步驟一個步驟進行教學，再進行練習。這樣的教學，學生只是跟著教師安排的節奏走，并沒有實質地參與到學習當中。怎么讓學生的學習經歷更有價值？有時，化終為始，逆向思維，能引發學生更積極主動的學習體驗。

比如《負數》一課的學習，從對教材的整體把握，再到學生的生活經驗及數學現實，我們了解到，負數對學生來說雖是新知，但并非一無所知。學生在生活中對負數有一定的認識，比如在天氣預報、電梯的乘坐、微信支付中，知道負數在生活中所表示的意義，甚至有一定的數學認識，會讀、會寫負數。在把握學生已有認知的同時，我們還了解到學生對負數有哪些困惑，在認知的過程中又存在什么樣的困難。

有了學情的把握，如果教學還是結合溫度計這一載體，讓學生創造符號表示，緊接著引入認識負數。那么課堂只是重復“用負數表示零下溫度”等學生已經知道的知識，這樣就體現不出應有的意義與價值。

雖然學生已經知道了負數，但就負數這一符號的抽象性來說，大部分學生的認識是模糊的。這一課的學習任務要如何設計，才能真正點燃學生的學習熱情？圍繞學生的認知水平和需求，把學習任務設計在學生的需求處、困惑處。比如將“體會負數的產生及其意義”確定為學習目標之一，同時將這一目標轉化為可探究、可理解、可言說的學習任務：假如這世界沒有負數可以嗎？請說明理由。

這一學習任務既考慮到學生已有的經驗，又考慮到未知的盲區，突顯學生的認知盲點與困境，引發其認知沖突與循疑探奇的渴求。當學生借助嘗試和經驗，建立現實與數學之間的鏈接，發現不能真正解決問題時，就會迫不及待地打開不同的視角，從生活的需求切換到數學的內部思考，主動發現，剖析說理。最終不僅從自然背景和人為規定等實例中，感悟到負數產生的意義；還從數學減法封閉的角度體會到引入負數的必要性。如此，負數的認識真正地嵌入到學生的精神世界，更因為全身心投入而抵達真實的學習，學會用自己的方式學習，對學生自身來說更具有價值。

三、融多為一，讓任務有創造

好的任務設計，可以打破學科的邏輯、打破教學的常規，從學生的經驗和思考的邏輯入手，選擇并設計開放的、挑戰的任務，為學生提供學習載體的同時，挑戰學生的思考廣度與認知深度，啟發學生自己判斷，自覺地反思自己的想法，跳出固有思維的框架，打開多種的可能視角，來到更廣闊的視野里，使自己的觀點獲得更新迭代。在這其間，既于嘗試探究中產生個性化的學習，又發現自己的潛能，創造出更多的可能性。

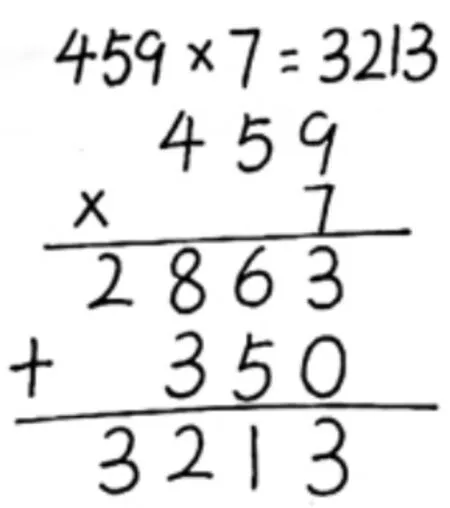
如《三位數乘一位數》一課，課堂在學生獨立列豎式計算“459×7”之后，出示了淘氣的做法（如上圖），啟發學生質疑：淘氣這樣做對嗎？這一學習任務，無疑是充滿活力的，又是寬泛開放的，既是對學生固有觀念的深挖和挑戰，沖擊著學生原有封閉的豎式算法的認知；又直指本質，啟發向“對不對”背后的真理及其求知路上的經歷發起深刻的追問；還挑戰學生大膽求異及創新思維。可以說，這一任務的設計，不僅把算法和算理的理解、常規算法與非常規算法融匯在一起，更把運算的多樣、靈活、合理等包容為一體，融多為一，既真實又貼切，一下子就觸及學生的“好奇心”，引發各種可能的生長。

在這一挑戰中，每個學生都基于自己的經驗和思考，把自己融入到團隊協作里，圍繞對立的兩個觀點，在一次次的對弈與思維交鋒中，不斷鮮明彼此的觀點，又不斷得到突破。其間，既有“為什么把350 寫在下面”“為什么跳過十位先算百位”“為什么還要加上350”等不斷的質疑，又有“先算409×7，再算50×7”的解讀，“只要算對就可以”的回擊；既生長出“換位思考一下，不要一直想自己”的智慧，“其實問題的本質都一樣”的真理；又于“我再舉個例子說理”中引發了新思辨，從“對不對”的說理走向“好不好”的分析，提出“有如111×1～111×9 等簡單題目不需要用淘氣算法”的新觀點……一次次的思維拐點，不斷挑戰著學生從算法走向算理，從墨守成規走向開拓創造，從算法多樣走向靈活合理，最終獲得“算法只是知識，選擇才是智慧”的深刻領悟，潛能不斷得到開發，同時獲得滿滿的成就感與掌控感。

有體驗、有價值、有創造的學習，不僅表現在學生的學習能力上，也表現在教師的教學智慧上。我們希望透過好的學習任務設計，不僅解決學科內的問題，更向所有學生的學習發起挑戰，幫助學生實現真實的學習，感受到數學的魅力，體會到學習的價值，催生出更多可能的創造與生長，看見自己的成長，發現自己的潛能，從內心生發出自信的力量。