巧用比較策略 促進深度理解
——南欲曉老師《速度、時間、路程》教學片斷賞析

文|張曉鋒

近期參加了一次研課活動，欣賞了浙江省杭州賣魚橋小學南欲曉老師執教的《速度、時間、路程》。本課學習活動設計精妙，巧用多次比較促進學生對較為抽象的速度概念的理解，讓“速度=路程÷時間”等常見數量關系的種子在學生心中扎根、生長。學生在學習過程中，對速度的內涵不僅知其然，而且知其所以然。本文通過片斷來洞悉南老師的匠心設計與精彩演繹。

片斷一：創設生活情境，激活比快慢的經驗

學生觀看蘇炳添參加東京奧運會短跑比賽的一段視頻。

師：同學們，你們知道跑步比賽比的是什么嗎？誰跑得最快？

（屏幕顯示蘇炳添東京奧運會100 米半決賽跑出9.83 秒）

師：100 米跑了9.83 秒，這句話里面藏著什么信息呀？

生：100 米是跑道的長度，9.83 秒是跑的成績。

師：這個成績我們常常指的是什么？

生：時間。

師：100 米是跑的長度，在數學中有一個自己的名字，叫路程。

（板書：路程）

師：蘇炳添跑100 米只要9.83 秒，人稱亞洲飛人。跑步比賽就是要比什么？

（板書：比快慢）

師：（演示跑步動作）今天我們就來比快慢，你會比快慢嗎？

生：可以這樣比，跑同樣長度，比時間，比誰花的時間少；還可以比同樣時間內，比誰跑得遠。

師：真厲害，他剛才說比快慢有兩種方法，大家聽懂了嗎？

（出示：a 同學走240 米，用時3 分）

（學生說出240 米指的是路程，3 分指的是時間）

（出示：b 同學走210 米，用時3 分；c 同學走240 米，用時4 分）

師：a 跟b 比，誰快誰慢？a 跟c 比，誰快誰慢？你是怎么比的？

生：a 同學走了240 米，用時3 分鐘，b 同學只走了210 米，用時也是3 分鐘。a 同學走的路程比b 同學多，但時間是一樣的，所以a 同學快。

師：什么一樣，什么多，就快？

生：他們用的時間一樣，但是a 比b 走的路程更遠，肯定a 快。

師：時間一樣，a 同學的路程多，所以就快。那么a 跟c 比呢？

生：他們走的路程是一樣的，但是用時是c 比a 多1 分鐘，所以a 同學快。

師：路程一樣，時間少了就快；時間多了，反而慢。

生：對，路程一樣，比時間。

【賞析：南老師從蘇炳添參加東京奧運會的短跑成績聊起，聊到了怎么比快慢，再結合學生走路比快慢，通過兩次比較，引導學生基于已有生活經驗，總結出“當時間一樣，誰的路程多，誰就快；當路程一樣，誰的時間少，誰就快。”比較過程非常自然，有利于學生明確比快慢的兩種不同比較路徑。】

片斷二：通過數形結合，優化比快慢的方法

師：現在又來了d 同學。a 同學走240 米用時3 分鐘，d 同學走180 米用時2 分鐘。a 和d 到底誰快誰慢呢？

［交流學生算式：a：240÷3=80（米），d：180÷2=90（米）］

師：240 米是a 的路程，3 分鐘是a 的時間，80 米是什么意思？

生：a 同學每分鐘走80 米。

師：我要把他說的哪個詞寫下來？走了多少米？

（板書：每分鐘80 米）

師：如果把240 米畫出來，把3 分鐘也畫出來。現在這個圖里缺了什么？我該怎么把它畫出來？

生：把240 米平均分成3 份，每份的長度就是每分鐘的長度。

（動畫分步演示3 個80 米累加，如下圖）

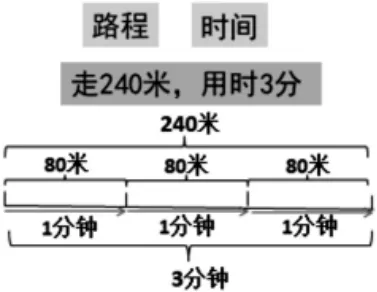
師：240 米被1 分鐘、1 分鐘、1 分鐘地平均分成了幾份？這80米還“藏”著什么？

生：每分鐘。

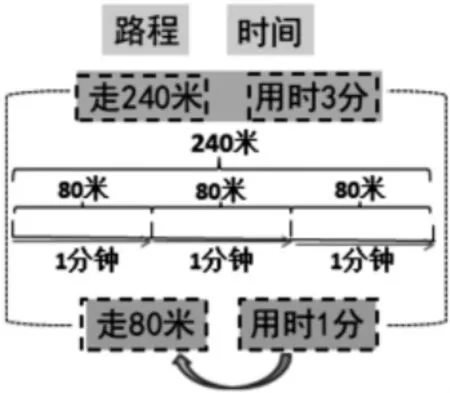
師：這位同學不是用3 分鐘走240 米比的。他把3 分鐘變成了多少？那240 米就被分成了3份，每份多少米？原來他是把時間變成1 分鐘，路程就被分成只有80 米，如下圖。

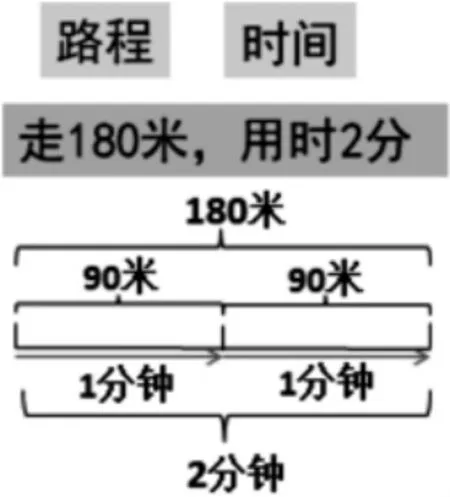
師：你能說說第二個算式里的90 米該怎么得到嗎？

生：把180 米平均分成2 份，每份是90 米。

師：用1 分鐘去分，得到90米，還有1 分鐘，也是90 米。原來這90 米是1 分鐘、1 分鐘分出來的，如下圖。

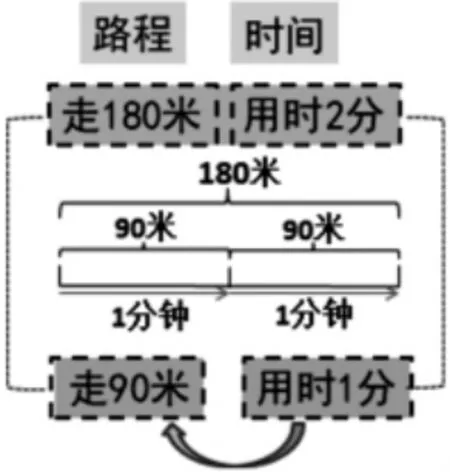
師：把2 分鐘變成1 分鐘。用180 米除以2 分鐘，得到90 米。這樣1 分鐘對應90 米，如下圖。所以誰快，是不是就知道了？

師：你們把3 分鐘、2 分鐘都變成1 分鐘。1 分鐘80 米，1 分鐘90 米，用的是剛才哪個比較方法？

生：時間相同，比路程。

師：誰還有不一樣的方法？

［呈現學生資源：180÷2=90（米），90×3=270（米），270 米＞240 米］

師：他用的是哪種方法？

生：時間相同，比路程。

師：270 米是誰走的路程？對應幾分鐘？240 米是什么意思？240米也對應3 分鐘。現在知道怎么比了嗎？

師：看來你們都喜歡第一種方法。時間一樣，比路程。

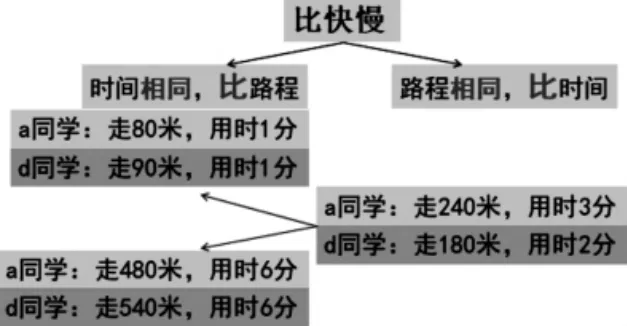
師：他把時間定為1 分鐘，他把時間定為3 分鐘，我把時間定為6 分鐘，都行！你最愛把時間定為幾分鐘，比快慢最方便？

生：我認為最方便的方法應該是把時間變成1 分鐘。

師：有同學將路程變相同嗎？

師：一般的人都會選擇時間相同；時間相同時，一般的人又選擇把它變成1 分鐘，這樣比較方便。

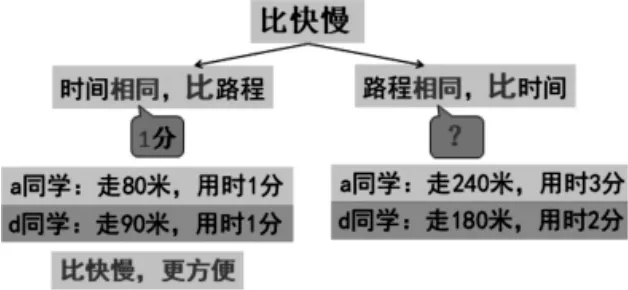
【賞析：華羅庚先生說：“數缺形時少直觀，形少數時難入微；數形結合百般好，隔離分家萬事休。”南老師通過數形結合的方式對“走240 米，用時3 分”和“走180 米，用時2 分”判斷誰快誰慢進行多維比較，直觀形象，豐富學生的感悟，在學生理解“把時間定為1 分鐘、3 分鐘、6 分鐘都可以”時，進一步優化方法，明確“時間一樣比路程”，促進學生自主建構“把時間定為1 分鐘比快慢更方便”的認識。南老師以學為中心，順應學生的思維，在引導學生多元表征速度的同時，促進學生深度理解。】

片斷三：構造問題情境，豐富比快慢的感知

（出示蘇炳添6.43 秒跑60 米的圖片）

師：大家從這個計時牌上看到了哪兩個數學信息？

生：我們可以看出他跑的路程和時間。

師：他跑60 米用6.43 秒，他跑得快還是慢呢？

師：假如跑60 米，時間沒有了，會——？同桌說說看。

生：跑60 米，假如沒有時間，比賽就決不出勝負。因為你跑得再快，沒有時間也是白跑！

生：我覺得如果他花的時間很久的話，別人會認為他非常慢。

師：如果沒有時間，那就沒有勝負。勝負換個詞就是什么？

（教師圈出黑板上的“快慢”）

師：如果時間丟了，就把什么也丟了？那就是把快慢也丟了。

（課件呈現：假如跑了60 米，用時1 秒，那——）

生：1 秒有點太快了吧。1 秒非常短，我覺得人家還沒反應過來他就到了。

師：大家看窗外，自己想象看到60 米的地方，目光穿越出去，嗖一下就到了！

師：蘇炳添會對他說什么？

生：你也太快了吧！是神仙嗎？

（課件繼續呈現：假如跑了60米，用時1 分鐘，那——）

生：我覺得那也太慢了，我50米測試只用了11 秒多。

（課件繼續呈現：假如跑60米，用時1 小時，那——）

師：請一個同學演一演，給他1 個小時，跑60 米。

師：假如在60 米后面加上時間，會有什么感覺？

生：我認為有了時間才會有快慢的感覺。

師：有了時間就有了快慢的感覺。沒時間不行，有了時間亂來也不行。請看下圖連線。

師：烏龜60 米，缺了時間？獵豹30 米，缺了時間？光30 萬千米，缺了時間？請你把時間送給它們。想一想，連一連。

師：烏龜爬60 米，送它什么時間？你為什么送它1 小時？

師：我們都知道龜爬形容慢，所以60 米，烏龜慢慢爬要1 個小時。如果獵豹1 分鐘跑30 米，蘇炳添會告訴它什么？

生：太慢了，所以獵豹跑30米要1 秒。

師:看外面30 米處，嘀嗒，獵豹到哪兒了？那么光呢？

生：我覺得也是1 秒，因為光年是測量宇宙的，宇宙無邊無際，要把每秒傳播速度拉得大一點，所以用1 秒。

師：光是目前世界上最快的，所以選擇時間1 秒。滴答一下，30萬千米，超級快！

【賞析：南老師結合蘇炳添6.43 秒跑60 米創設了一個連環情境，設計四連問：“假如跑60米，時間沒有了，會——”以及“假如跑60 米，用時1 秒、1 分、1 時，那——”，引發學生想象、思辨、調整，教師還與學生一起演示快慢不一的運動狀態，讓學生在表達、演示、比較的過程中真切而強烈地感受比快慢與長度、時間兩個量有關，缺一不可，增強有了時間才會有快慢的感覺。看圖連線題設計了一組學生較為熟悉的自然現象，引領學生在多向交往中加深體驗與感悟，尋找合適的參照，如與自己跑步比較，與蘇炳添跑步比較，豐富學生對速度的感知，在多元對比中不斷滋養學生的量感。】

片斷四：設置認知沖突，深化學生對速度的理解

（出示閱讀材料，學生完成練習）

師：請你找到他們爭論的問題在哪里？

生：這里的問題是，雖然他們的路程是一樣的，但他們的時間是不一樣的。“神七”飛船是1 秒鐘飛8 千米，而小青騎自行車是1個小時才前進了8 千米。完全不是一個等級！

師：問題在8 千米身上對不對？為什么會有這樣的問題呢？

生：因為比了路程，沒有比時間！

師：8 千米丟掉了什么？

生：時間。

師：第一個8 千米用1 秒，第二個8 千米用1 小時，在答案上怎樣才能把秒、時給帶上呢？

生：加一個斜杠。

師：加一個斜杠？再加個什么？

學生補充：再加個1 秒。

師：1 秒還是秒？誰知道怎么讀？

（教師指著8 千米/秒、8 千米/時引導學生讀出兩個數量）

師：真厲害，它們分別讀作8千米每秒、8 千米每時。

師：丟了的時間撿回來了嗎？

生：撿回來了。

師：我們來梳理一下。我們剛才研究了幾位同學、烏龜、獵豹、光以及“神七”飛船的相關數據。我們都是用來比什么的呀？

生：比快慢。

師：快慢身上藏著哪兩個信息？

生：時間和路程。

師：誰來找找看，這里時間和路程在哪里？用來比快慢的這些時間有什么共同的地方？

生：它們都是一個數字1，然后加一個單位。

師：真棒，一個數字1 帶一個時間單位就叫“一個單位時間”，就是1 分、1 秒、1 時。好，仔細看屏幕，路程在哪里？讀出來。

（學生讀出課件上所有路程，教師將這些路程圈出來）

師：我們都用一份的時間比出了這樣一份的路程，用來比較它們的快慢，數學上稱它為速度。我們以后不說比快慢了，就說比速度。如a 同學走路的速度是80米/分，b 同學走路的速度是90 米/分。當8 千米后面加“/小時”，兩個單位加在一起的時候就叫復合單位，可以用它來比快慢！

【賞析：南老師創設了一個鮮活的比較情境，激起學生的認知沖突，讓學生在平息自行車騎速和“神七”速度的爭論活動中自然產生使用一個新單位表示運動快慢的需求。這一刻，用來表示速度的復合單位順勢而生。南老師再通過對一組數量的聚類分析與比較，引導學生由選定一個單位時間比快慢的經驗深化對速度內涵的理解。】

片斷五：解決實際問題，引導學生完善認知結構

師：下圖是溫州到上海的路程和時間表。你們有辦法算出速度嗎？

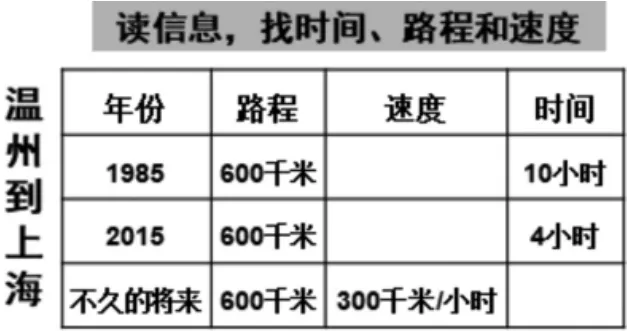
［呈現學生錯誤資源：600÷4=150（千米）］

師：請你們做老師，你們會給他什么建議？

生：我會建議他畫一個斜杠，加上另外一個單位———時。

師：如果把時間丟了，那就不是快慢了。你們自己說的，時間丟了，就跑輸了！

師：這個速度，是怎么算的？

生：用路程除以時間等于速度。

（呈現：速度=路程÷時間）

師：把這里的4 小時變成1小時，600 就變成了150。猜猜看，1985年的速度比2015年可能要怎么樣？如果時間是10 小時，你們會算速度嗎？請列出算式。

師：猜猜在不久的將來速度可能是多少？如果速度是300 千米/小時，會算時間嗎？

生：路程除以速度等于時間。

（呈現：時間=路程÷速度）

師：溫州到杭州大約有400千米，照這樣的速度計算，從溫州到杭州，3 小時能到嗎？

（學生計算，教師收集并呈現學生資源）

師：剛才算出的450 千米是什么？他是怎么算路程的呀？對，路程等于速度乘時間。

（呈現：路程=速度×時間）

【賞析：南老師聯系生活實際，以溫州與杭州之間的距離為素材設計練習，將求速度與求時間等問題融于一題，在加深學生對速度概念認識的同時，幫助學生自主建構對常見數量關系“速度=路程÷時間”“時間=路程÷速度”“路程=速度×時間”的認知，培養學生在真實的問題情境中自主分析問題、解決問題的能力，同時滲透函數思想，即路程一定時，速度與時間成反比例關系。】