單元視角 結構教學
——《小數的意義》教學設計

文 朱俊華

【教學內容】

蘇教版五年級上冊第30～32頁例1、“試一試”和“練一練”，練習五第1～6 題。

【教學重、難點】

理解并抽象小數的意義，體會小數與分數、整數的聯系。

【教學準備】

教具：無刻度的1 米尺、有分米和毫米刻度的1 米尺各一把。

學具：每小組各一把分米刻度的1 米尺、學生尺。

【教學過程】

一、系統呈現，喚起一位小數認知經驗

師：同學們，今天老師帶來了一把特別的米尺。特別在哪呢？

生：只有1 米這個刻度，沒有其他的刻度。

師：用這樣的1 米尺能測量黑板的長嗎？

師：用這樣的米尺還能測量哪些長度呢？（1 米、5 米……）

明確：用這樣的米尺可以測量1 米、2 米、3 米……較長的整米數長度，我們通常用“整數”表示。

探究：你能用這把米尺量出課桌的寬嗎？

活動：請同學們嘗試“改造”這把不完整的米尺，使得它能夠測量課桌的寬度。

交流：把1 米尺平均分成10份，每份就是1 分米，用米作單位是米，用小數表示就是0.1米。

交流：現在用這把改造過的米尺來測量課桌的寬是多少米。

分享：把1 米平均分成10份，4 分米是這樣的4 份，是1 米的，是米，也就是0.4 米。

師：接著往下數，0.5 米、0.6米……0.9 米，這些都是一位小數，就是十分之幾。

【設計意圖：小數是在實際度量的需要和整數運算中產生和發展起來的。借助自制的無刻度“1米尺”教具，從測量開始讓學生直觀感知“量”的累加，激活認識整數的經驗。以測量4 分米的課桌寬度為問題沖突，引發學生在“疑”中創造“分”，從而引入一位小數的復習，找準學生的認知起點，使新的學習材料與學生已有認知相聯結。】

二、邏輯推演，關聯小數與分數意義

1.直觀模型，建構兩位小數的意義。

談話：一位小數是我們的老朋友了，三年級時我們已經認識了。帶著這把米尺我們繼續測量，好嗎？

研究：課桌的高是多少米？

交流：課桌的高比0.7 米多一些，在0.7 米和0.8 米之間。

提問：課桌到底有多高呢？

活動要求：

（1）思考：怎樣準確測量課桌的高？

（2）實踐：把你的想法在學具尺上表示出來。

（3）分享：和同伴交流。

交流：將0.7 和0.8 之間再平均分成10 份，量得課桌高0.72 米。

生：把1 米平均分成100 份，每份是1 厘米，是1 米的，是米，也就是0.01 米。

師：同桌互說0.72 米表示的意義。

生：把1 米平均分成100 份，每份是1 厘米，表示其中的72份，是72 厘米，是1 米的，是米，也就是0.72 米。

追問：35 厘米又是多少米呢？大家互相說一說。

師：觀察0.01、0.35、0.72，它們有什么相同的地方？

生：它們都是兩位小數。

生：這些小數對應分數的分母都是100，表示百分之幾。

小結：回頭看看，我們是怎樣認識兩位小數的？

2.類推遷移，認識三位小數。

師：現在，我們知道一位小數表示十分之幾，兩位小數表示百分之幾，接著往下想，你能想到什么？

生：我還能想到三位小數，并且我猜想三位小數表示千分之幾。

思考：怎樣得到千分之幾呢？（調用“均分”的經驗）

生：每小格再平均分成10 份，有100 個這樣的10 份，是1000 份。

師：為了便于觀察，老師將這里的1 份取出來，放大，再平均分成10 份，想一下，把這里的每1份都平均分成10 份，可以分成100 個這樣的10 份，也就是1000份。

問：那這里的1 小份有多長？你會表示嗎？（指名說說：1 毫米、米、0.001 米）

明確：我們把1 米平均分成1000 份，得到每份是1 毫米，是米，也就是0.001 米。

師：這幾個長度，你也能用分數，小數表示嗎？在書上填一填。

3.推理聯想，認識更多小數。

師：想象一下，0.001 米還可以繼續分嗎？會得到哪些小數呢？（四位小數、五位小數……）

【設計意圖：學生的概念學習需要經歷一種經驗性的活動過程，從一位小數意義的認知激活，到兩位小數意義的精細刻畫，再到三位小數的類推遷移，從簡單到復雜，學生經歷了一個螺旋上升的認識模型的建構過程。在序列化、有層次推進教學的過程中，堅持數形結合的原則來理解小數的意義，同時把“抽象、推理、建模”的基本數學思想浸潤其中。】

三、結構關聯，勾連小數與整數關系

質疑：同學們，學到這你們有沒有什么疑問？

生：為什么一位小數、二位小數、三位小數……是把“1”平均分成10 份、100 份、1000 份呢？

師：同學們，通過“均分”，我們認識更多的小數，回憶一下，我們又是怎樣認識整數的呢？

（課件動態呈現）

【設計意圖：整體性理解基于數學知識的內在結構，通過知識之間的比較、關聯和遷移，實現知識的整體建構。小數和整數一樣都是建立在“十進制”基礎上的數，通過小正方體的“累加”“均分”，融通小數和整數之間的內在關聯，從整體上理解小數的形成和意義。】

四、遷移運用，題組對比中深化認知

1.在括號里填上合適的小數。

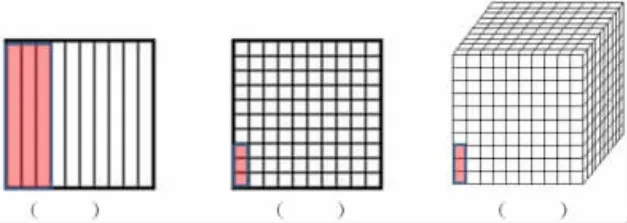
追問：涂色都是3 格，為什么表示的小數不同呢？

2.在數軸上填上合適的小數。

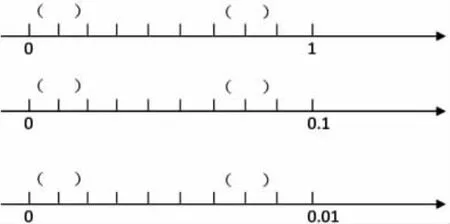
3.馬拉松比賽全程42.195 千米，請說一說這個小數的含義。

4.全課小結：通過今天的學習，你有哪些收獲？

【設計意圖：引導學生學以致用，靈活遷移用學過的知識解決數學問題，也是培養學生結構化思維的重要舉措。教師出示的三道題目分別是數形結合、數軸和生活中的小數，旨在幫助學生強化對小數意義的理解，同時也是讓他們進一步感悟知識的整體性。】