膠結充填體頂板承載層厚度的尖點突變模型及其應用

趙 奎 王萬銀 曾 鵬 龔 囪 梁 楠 李文輝

(1.江西理工大學資源與環境工程學院,江西 贛州 341000;2.江西省礦業工程重點實驗室,江西 贛州 341000)

下向水平分層膠結充填采礦法自20世紀60年代引入至中國,在高效回采、綠色礦山的大背景下,快速發展并廣泛應用在我國的金屬、非金屬礦山[1-2]。下向水平分層膠結充填采礦法自上而下回采礦體,采場回采進路上方的直接頂板為膠結充填體,膠結充填體頂板的穩定性是礦山安全回采的前提。為控制開采成本,通常膠結充填體頂板是由低灰砂比的充填體(接頂層)與高灰砂比的充填體(承載層)上、下布置組成[3]。其中,上部充填體(接頂層)強度低、力學性能差,難以發揮承載作用;而下部充填體(承載層)強度高、力學性能好,起主要承載作用[4]。然而,高灰砂比充填成本普遍高于低灰砂比充填。若承載層厚度設計太厚,將導致礦山開采成本增大;厚度太薄,則難以保障下分層回采作業的安全。因此,設計合理的承載層安全厚度對于采用下向水平分層膠結充填采礦法的礦山具有非常重要的現實意義。

目前,學者們對膠結充填體頂板承載層安全厚度的合理留設往往從梁、板力學模型出發結合可靠度理論或安全系數法進行分析[5-7]。該類方法在對承載層厚度的計算過程大都是半定量分析,難以真實反映頂板的力學狀態及損傷情況,因此計算結果與工程實際存在較大偏差[8]。研究表明[9],當采場承載層厚度小于臨界厚度時,充填體頂板發生突變失穩,其實質是充填體頂板位移從連續漸近變化至非線性躍變的變形過程。

隨著現代非線性理論發展,突變理論作為一種研究系統從連續變化到不穩定變化躍變的非線性數學模型,是巖土工程中穩定性分析的重要手段[10]。如白夢月等[11]基于強度折減法構建了不同安全系數下邊坡能量突變模型,計算得到許東溝礦下盤巖體邊坡安全系數為1.64;蔣騰飛等[12]采用圓錐臺力學模型簡化出巖溶基坑防突層失穩尖點突變能量判據,并推導出巖溶基坑防突層的厚度計算公式;杜崧等[13]基于突變理論以塊體突變級數的隸屬度值為評價指標,構建了多因素影響下地下洞室塊體穩定性評價模型。

有鑒于此,本文采用數值模擬研究不同承載層厚度下充填體頂板位移值,在此基礎上構建頂板位移尖點突變模型,根據不同承載層厚度下頂板位移突變特征值,得到充填承載層理論安全厚度,最后通過現場試驗驗證理論計算的可行性,為采用下向水平分層膠結充填采礦法的礦山承載層厚度設計提供依據。

1 承載層位移尖點突變模型

1.1 突變理論

尖點突變初等模型結構形式簡單,且能夠很好解釋因結構因素變化導致的整體工程突變失穩的現象,在巖土工程領域應用廣泛。其勢能函數是由1個狀態變量x以及2個控制變量a、b構成的一元多次函數,即:

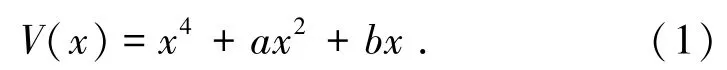
對式(1)求導可得到尖點突變模型的平衡曲面方程,即:

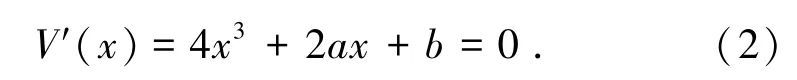
由式(2)可知,系統尖點突變模型的平衡曲面是由變量(x,a,b)構成的空間曲面M,如圖1所示。

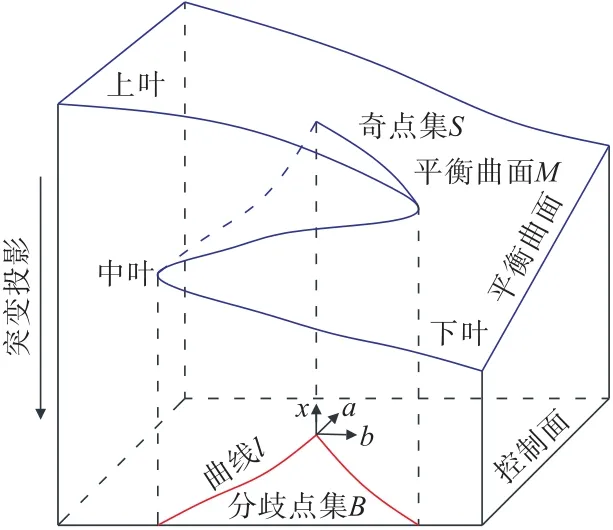
圖1 尖點突變模型平衡曲面Fig.1 Equilibrium surface of Cusp catastrophem odel

圖1中系統模型的平衡曲面在空間表現為1個兩側連續光滑、中間躍變褶皺的連續曲面,依據光滑程度可將曲面劃分為上葉、中葉、下葉3個區域。其中,上葉與下葉區域表示系統處于平衡穩定的狀態;中葉表示系統處于不穩定的狀態;上葉、下葉與中葉的交線表示系統由穩定狀態跨越到不穩定狀態的突變臨界點集,稱為奇點集S。它是由系統勢函數二階導數V″(x)=12x2+2a=0與平衡曲面方程的解集。曲線l為奇點集在a—b面中的投影,稱為分歧點集(也稱為突變點集),在a—b面上的函數方程為

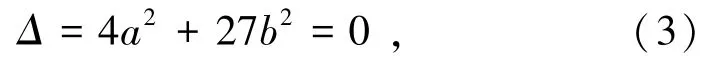
式中,Δ為分歧方程的解。

當控制因子(a、b)落在曲線l上時(Δ=0),系統處于臨界突變狀態;當控制因子(a、b)落在曲線l外時(Δ＞0),系統處于穩定平衡狀態;當控制因子(a、b)落在曲線l內時(Δ＜0),系統處于不穩定狀態。

1.2 位移尖點突變模型

研究表明[14-16],回采進路開挖后,充填體頂板中間部位發生的位移較其他部位更加明顯。隨著承載層厚度的變化,通過數值模擬軟件獲取回采進路開挖后充填體頂板中間部位的位移,對厚度、位移進行4次多項式擬合,得到位移—厚度的函數關系式:

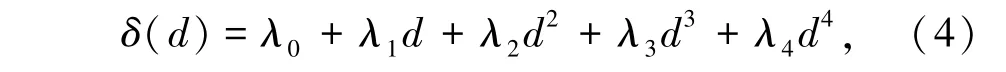
式中,λ0、λ1、λ2、λ3、λ4為待定參數。

引入無量綱參數d=x-α,代入式(4)進行變換,得:

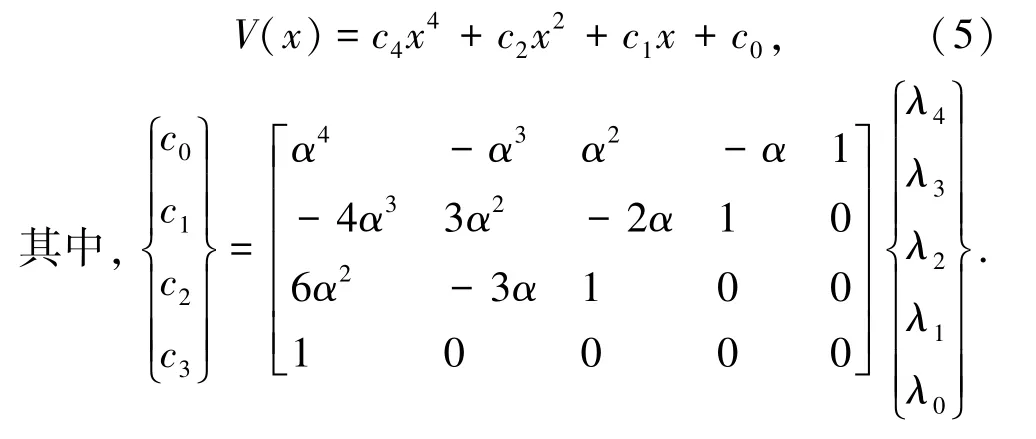
對式(5)進行變量代換,轉換為尖點突變模型得標準勢函數形式:

1.3 承載層安全厚度尖點突變模型計算方案

下向膠結充填采礦法中承載層安全厚度的計算步驟如下:

第一步,依據回采進路高度,設定足夠安全的承載層厚度初始值d0,通過數值模擬軟件,構建下向水平分層充填采礦法回采進路模型,得到回采進路開挖后充填體頂板的位移值。

第二步,按照一定梯度Δd,建立不同承載層厚度模型。其中,第i次計算承載層的厚度值為d0-iΔd。

第三步,繪制不同承載層厚度頂板中間位移的散點圖,由式(4)構建出位移尖點突變模型。

第四步,計算不同承載層厚度的位移突變特征值Δ,確定位移發生突變的承載層厚度di,將發生突變前一次的厚度di-1視為承載層的安全厚度。

第五步,輸出發生位移突變的回采進路模型計算結果中的最大主應力云圖、塑性區分布圖,驗證位移尖點突變模型計算結果的可靠性。

具體計算分析流程圖,如圖2所示。

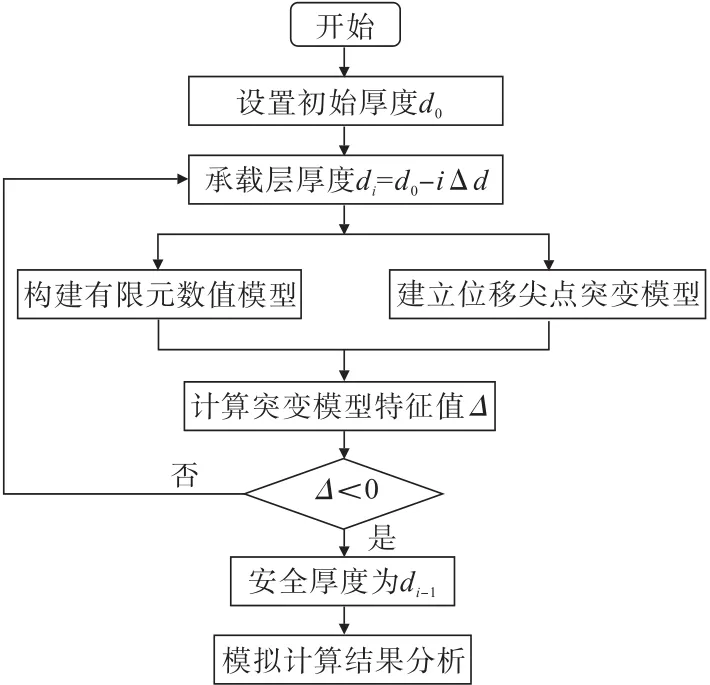
圖2 計算分析流程Fig.2 Cornputational analysis process

2 工程應用

某銅礦山采用下向水平分層膠結充填采礦法,中段高度40 m,主要生產采場標高為-360 m,設計回采進路斷面尺寸(跨度×高度)為5 m×4 m,承載層為灰砂比1∶4的膠結充填體,接頂層為灰砂比1∶8的膠結充填體,相關物理力學參數見表1。

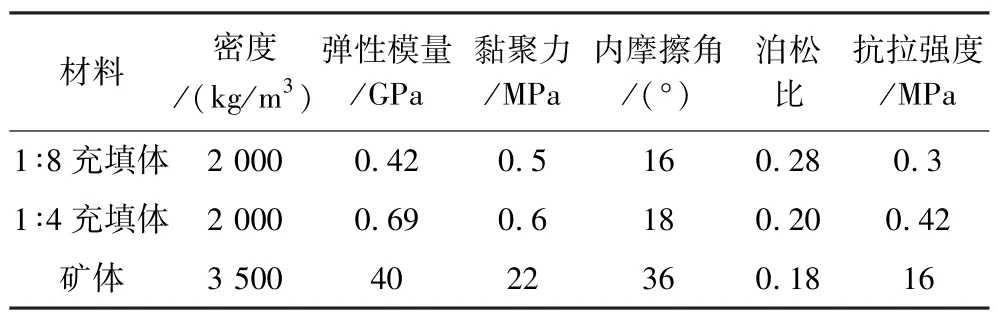
表1 相關物理力學參數Table 1 Relevant physical-mechanical parameters

2.1 數值模型

根據礦山生產實際,采用ABAQUS數值軟件構建回采進路開挖模型,為消除模型邊界約束對計算結果的影響,設置模型整體尺寸為回采進路開挖尺寸的4倍(長×寬為20 m×16m)。模型整體為平面應變模型,網格劃分類型為四邊形網格,模型計算著重研究回采進路開挖后充填體頂板的變化特征,回采進路上方充填體網格尺寸控制為0.2 m,回采進路下方礦體尺寸控制為0.4m,共6 060單元,6 222節點,圖3為承載層厚度2 m時的網格模型。其中,實面①代表1∶8充填體,實面②代表1∶4充填體,實面③代表礦體。

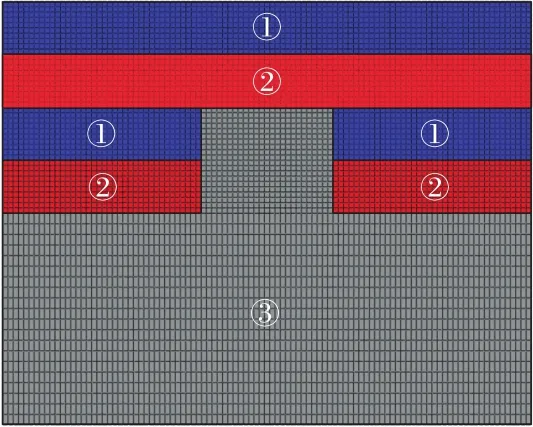
圖3 回采進路模型Fig.3 Model of stoping route

為保證模型計算承載層安全厚度的可靠性,在設計工程條件時,應盡量選擇最不利于承載層穩定的工程結構,模擬時作如下假設:回采進路兩幫為充填體,該工況下充填體頂板穩定性最差[17]。該采場上覆充填體高度為30 m,模型底部及兩側指定位移邊界約束。

2.2 計算結果及分析

設定承載層厚度初始值d0為3 m,建立不同承載層厚度計算模型,模擬各厚度下回采進路開挖后的充填體頂板的力學狀態。選擇充填體頂板中點作為位移監測點,監測記錄不同承載層厚度下回采進路開挖后監測點位移值,監測點示意如圖4所示,計算結果見表2。

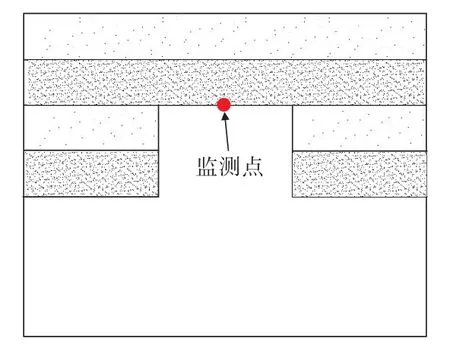
圖4 監測點示意Fig.4 Schematic of monitoring point

由表2可知,監測點位移值隨承載層厚度的減小呈現遞增趨勢。對數據進行擬合,并將擬合后數據代入式(6)與式(3)中,計算位移尖點突變模型的突變特征值Δ。其中,不同承載層厚度下監測點位移擬合曲線如圖5所示,位移突變特征值隨承載層厚度變化曲線如圖6所示。

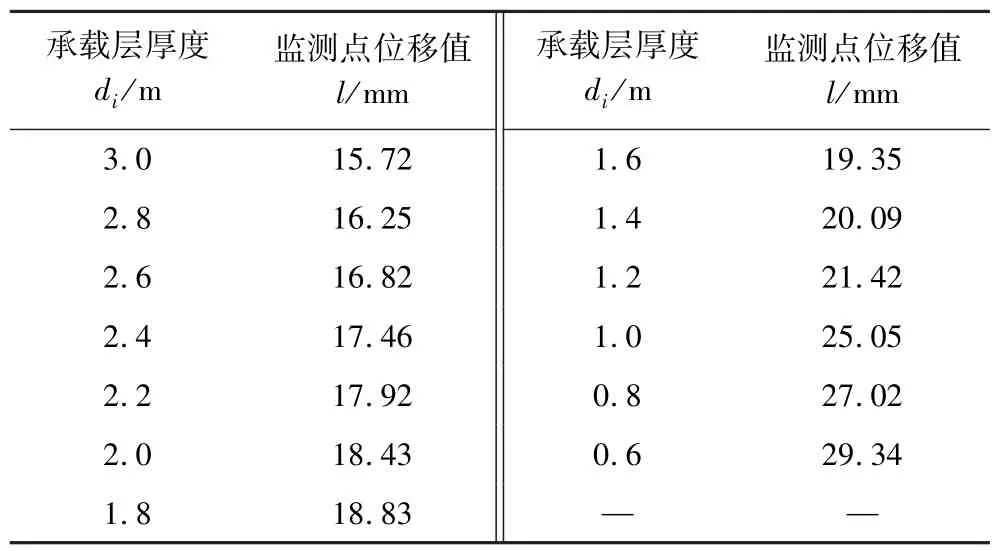
表2 不同承載層厚度監測點位移值Table 2 Displacement values of monitoring points with different bearing layer thickness

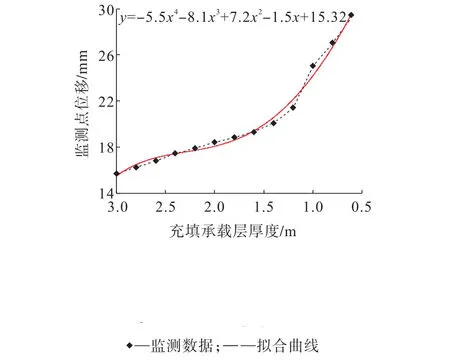
圖5 監測點位移擬合曲線Fig.5 Displacement fitting curves displacement of monitoring points

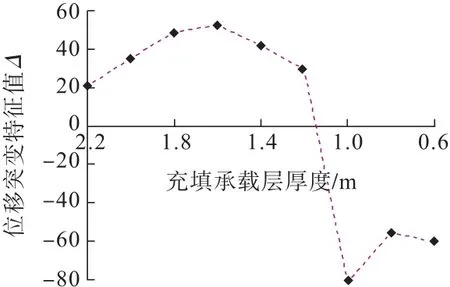
圖6 位移突變特征值隨承載層厚度變化曲線Fig.6 Variation curve of displacement catastrophe eigenvalue with bearing layer thickness

由圖5可知,承載層厚度減小至1.0 m前,監測點位移值隨承載層厚度的折減緩慢增長,增長曲線近乎線性;承載層減小至1.0 m時,監測點位移值相較于承載層厚度為1.2 m時發生較大程度變化。由圖6可知,承載層厚度減小至1.0 m時,位移尖點突變模型特征值小于0,發生突變,說明此厚度下回采進路開挖后充填體頂板發生失穩破壞。由圖6可得出,當回采進路斷面為5 m×4 m時,膠結充填體頂板承載層的安全厚度為1.2 m。

2.3 位移突變區間結果分析

為驗證承載層安全厚度計算結果的可靠性,基于ABAQUS軟件的可視化窗口,輸出承載層厚度為1.2、1.0 m時,模型的最大主應力云圖、塑性區分布圖,如圖7、圖8所示。

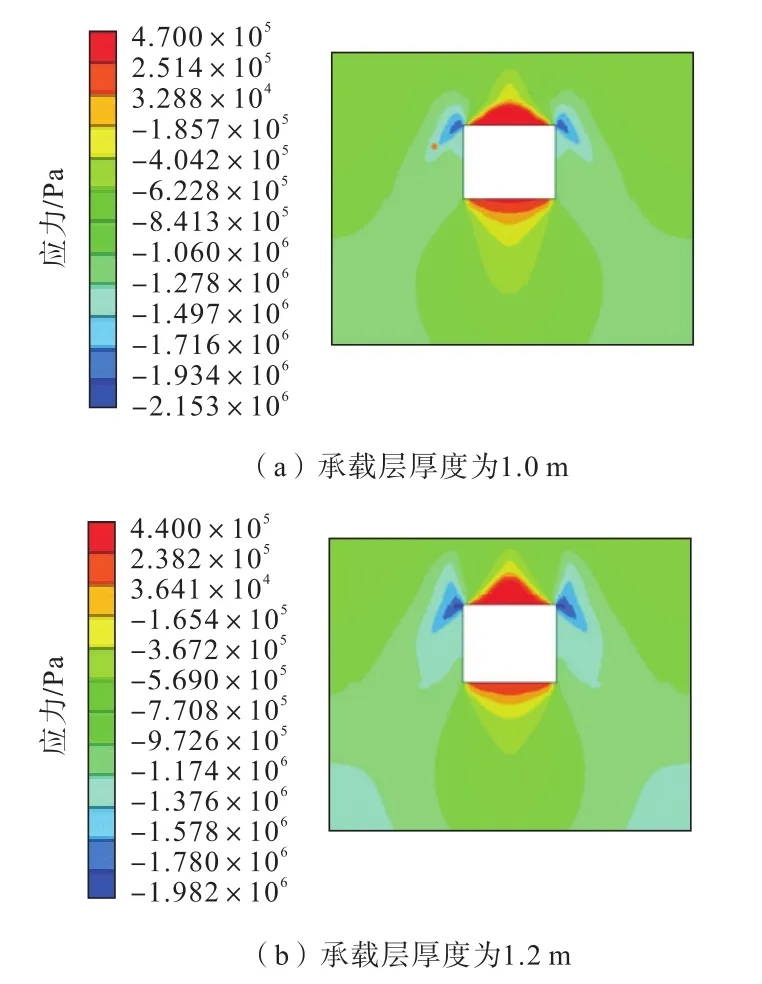
圖7 最大主應力云圖Fig.7 Nephogram of maximum principal stress

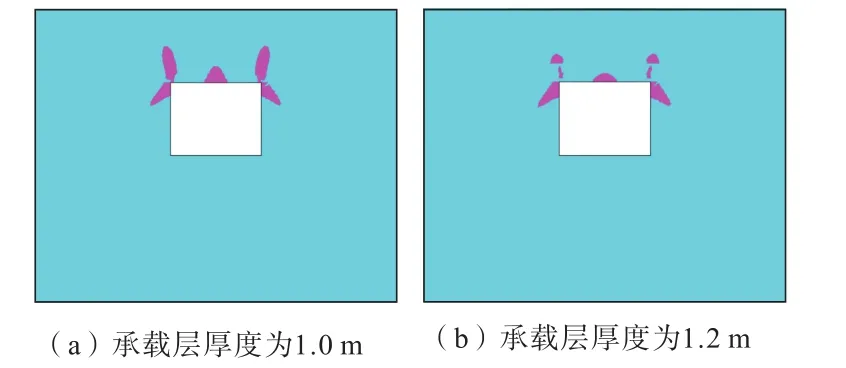
圖8 塑性區分布Fig.8 Distribution of plastic zone

由圖7可知,回采進路開挖后,進路頂板、底板處拉應力集中,進路兩幫壓應力集中。其中,當承載層厚度為1.0 m時,頂板中的拉應力極值0.47 MPa,壓應力極值2.15 MPa;當承載層厚度為1.2 m時,頂板中的拉應力極值0.44 MPa,壓應力極值1.98 MPa。2種厚度下,頂板拉應力極值均大于承載層充填體的抗拉強度,承載層厚度為1.0 m時,頂板應力集中更明顯。

由圖8可知,回采進路開挖后,充填體頂板在進路中間發生拉裂破壞,在進路兩側發生剪切破壞。當承載層厚度為1.0m時,頂板在回采進路進路中部及兩側均出現連續的塑性破壞,頂板中間及兩側塑性區分布長度超過了承載層厚度,頂板發生失穩破壞;當承載層厚度為1.2 m時,頂板兩側塑性區分布不連續,中間塑性區分布長度未超過承載層厚度,頂板內產生了一定面積的塑性破壞,頂板處于臨界失穩狀態。

由以上分析可知,當承載層從1.2 m減小到1.0 m時,承載層作為回采進路充填體頂板發生失穩破壞,驗證了位移尖點突變承載層安全厚度計算結果的可靠性。

3 工程實際效果

根據計算得出的承載層安全厚度值,綜合考慮實際生產中影響充填體頂板穩定性因素,如爆破振動等。同時結合礦山的實際操作性,最終推薦當回采進路斷面為5 m×4 m時,充填承載厚度值為1.5 m。

為驗證承載層安全厚度的可靠性,在S2采場15分層7分條回采進路充填前,預先埋設應力計、應變計2種監測儀器,儀器分別豎向布置在充填體頂板接頂層與承載層內部。當下一分層回采時,監測15分層的充填體作為頂板被揭露前后的變化特征。其中,圖9為回采下一分層時位于接頂層與承載層內部的應力計監測結果,圖10為相應的應變計監測結果。

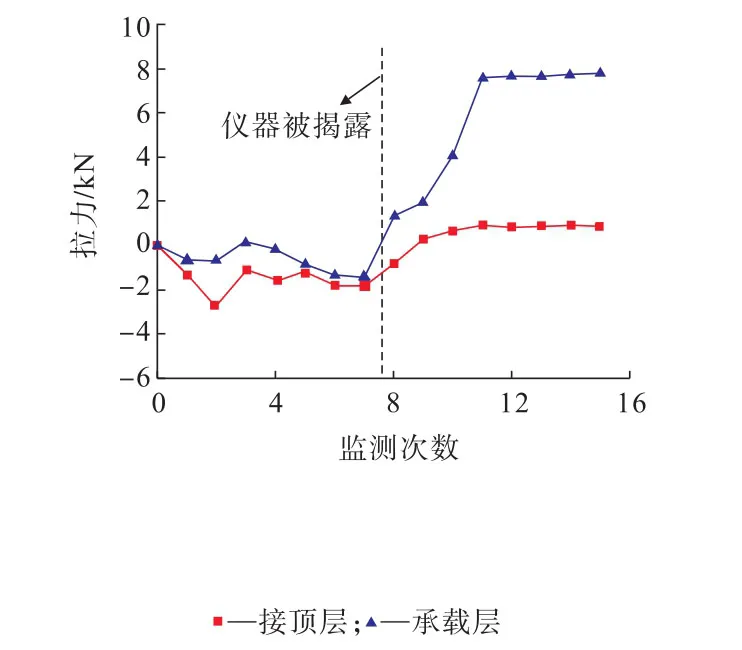
圖9 應力計監測結果Fig.9 Results of stress meter monitoring

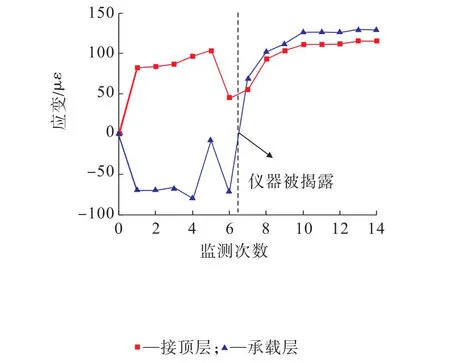
圖10 應變計監測結果Fig.10 Results of strain gauge monitoring

現場監測結果表明,膠結充填體作為頂板被揭露前后,頂板力學狀態變化幅度小,承載效果好。其中,頂板揭露后,最大拉力值為7.8 kN,應變最大值小于150με,在充填體頂板安全變形范圍內[18]。圖11為回采下一分層時上一分層膠結充填體頂板被揭露后照片,充填體頂板整體性好、無明顯異常區,保障了進路采場的安全。

圖11 膠結充填體頂板照片Fig.11 Site photos of cemented filling roof

4 結 論

(1)根據下向水平分層膠結充填采礦中充填體頂板位移非線性變化特征,建立了頂板位移尖點突變模型,得到了不同承載層厚度下模型位移突變特征值,提出了充填承載層的安全厚度計算方法。

(2)結合礦山工程實際,基于ABAQUS有限元數值軟件,構建了斷面尺寸為5 m×4m的回采進路開挖模型,計算了不同承載層厚度下回采進路開挖后的充填體頂板位移值及位移突變特征值。計算結果表明,當回采斷面尺寸為5 m×4m時,承載層厚度小于1.2m時,進路頂板兩側拐角處形成連續塑性區;承載層厚度為1.0～1.2 m時,位移突變特征值由正值向負值發生躍變,頂板發生失穩破壞。

(3)現場監測結果表明,當承載層厚度為1.5 m時,膠結充填充填體頂板揭露過程中力學狀態變化小,能有效發揮承載作用,保障了礦山采場生產作業安全。進一步驗證了該方法的合理性,為采用下向水平分層膠結充填采礦法的礦山承載層厚度的設計提供了依據。

致 謝

感謝伍文凱博士、楊賢達博士對數值模擬的建議和幫助及宋林碩士、王金鑒碩士、劉周超碩士、楊澤元碩士、謝文健碩士、劉光清碩士、劉光卓碩士、李智偉碩士、王星碩士、楊溪碩士對現場試驗的幫助!