強降雨場景下自適應巡航控制系統的安全控制策略*

趙 超，卜德旭，曹禮鵬，2，李克強，羅禹貢

（1. 清華大學車輛與運載學院，汽車安全與節能國家重點實驗室，北京 100084；2. 重慶大學機械與運載工程學院，重慶 400030）

前言

自適應巡航控制（adaptive cruise control system，ACC）是重要的智能駕駛輔助功能，ACC 系統的目標為通過控制驅動系統和制動系統自動調整車速實現車距保持功能。ACC 可以有效減輕駕駛員疲勞強度，提升駕駛的安全性與舒適性。ACC 系統功能的實現依賴于毫米波雷達感知信息的正確性，毫米波雷達在強降雨場景下的性能局限性，可能會導致ACC系統出現速度控制錯誤的預期功能安全問題。

預 期 功 能 安 全（safety of the intended functionality，SOTIF）的定義是沒有因預期功能的功能不足或可合理預見的人為誤用導致的不合理風險。ISO 21448 標準提供了實現SOTIF 所需的適用設計、驗證和驗證措施的指南，還有研究提供了一些風險評估和觸發條件的確定方法，但是目前針對“功能改進來降低SOTIF 風險”的策略的研究較少。

毫米波雷達是ACC 的重要組成元件，目前的研究重點都在于改進常規工況下ACC 的性能，提升毫米波雷達測量的實時性與準確性，確保目標識別與跟蹤的效果，但是對于ACC 系統在強降雨環境下出現的SOTIF問題考慮較少。

強降雨帶來的衰減、雜波和噪聲會降低毫米波雷達的最大檢測范圍，增大虛警概率和測量誤差。雨衰減和后向散射會使目標回波功率降低、雜波功率增加。王輝考慮了大氣衰減和后向散射，對地面、海面、雨和雪條件下的9.5-95 GHz 之間所有常用的雷達的反射進行了一系列研究。黃際英等使用Mie 理論計算了單個球形雨滴在不同溫度、不同工作頻率、不同尺寸情況下的衰減截面和后向散射截面，使用統計擬合的方法，得到了計算毫米波段雨介質后向散射系數的簡單公式。Gourova 等在雨霧隧道中進行了毫米波雷達的探測實驗，對后向散射進行了理論分析。在高頻與粒子數目較大的情況下，多重散射會使得降雨后向散射增強。白繼玲等分析了降雨的多重散射效應，計算了由降雨的2 階散射機制造成的雨雜波回波功率。Yang 等討論了離散隨機介質中2 階后向散射增強理論，基于Mie 理論、蒙特卡羅模擬和后向散射增強理論，分別在35 和95 GHz 時分析了降雨對毫米波雷達性能的影響。此外，考慮降雨對天線噪聲溫度的影響，張蕊等擬合得到了由降雨的雷達體反射率反演雨衰減率的公式。 Zang 等模擬了降雨場景下毫米波雷達的返回功率和接受功率信噪比的變化。李鑫的研究表明，降雨對毫米波雷達返回功率的影響會使毫米波雷達虛警概率增大，最大檢測距離降低和測量誤差增大。總體而言，當前研究主要集中在分析降雨對毫米波雷達性能影響分析方面，未考慮毫米波雷達的性能局限可能造成的自適應巡航控制系統的SOTIF 問題，同時未涉及相應的安全風險識別和安全控制策略的研究。

本文中提出了強降雨場景下ACC 系統的安全控制策略，旨在降低由強降雨導致的ACC 系統性能局限的SOTIF風險。首先使用雙狀態識別可能影響ACC 性能的安全風險，將毫米波雷達觀測信息輸入到卡爾曼濾波器和兩個狀態遞推器當中，通過比較卡爾曼濾波器和狀態遞推器的差值判斷系統是否存在安全風險；其次，使用卡爾曼濾波對存在安全風險的毫米波雷達觀測信息進行修正，將處理修正后的信息輸入ACC 上層控制器，基于PID 控制得到期望加速度，下層控制器將期望加速度轉化為驅動信號或制動信號對車輛進行控制；最后搭建Prescan/Simulink 聯合仿真平臺對所提安全控制策略進行驗證。

1 毫米波雷達SOTIF問題描述

強降雨環境中，毫米波雷達回波功率降低，雨雜波和噪聲功率增加。強降雨條件下，雨衰減會使目標回波功率降低，此時目標的回波功率為

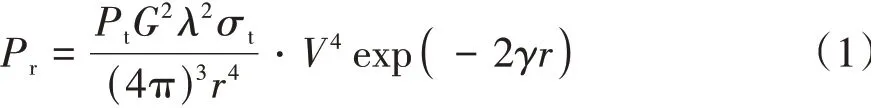
式中：為目標的返回功率；為發射信號功率；為雷達天線增益；為毫米波雷達工作波長；為目標雷達散射截面（RCS）；為多路徑系數；為衰減系數；為雷達與目標之間距離。

式中：為雜波信號功率；為脈沖持續時間；為天線波束寬度；為雨滴的后向散射系數。

式中：為噪聲功率；為接收機噪聲數據；為噪聲溫度；為玻爾茲曼常數；為接收機濾波帶寬。

毫米波雷達對于運動信息的測量受毫米波雷達接受功率信噪比的影響。噪聲、雜波導致的毫米波雷達速度測量誤差為

式中：為雷達回波信號功率；為噪聲和雜波的總功率；Δ為雷達調頻帶寬；為雷達調頻周期；為雷達處理時的積累時間。

毫米波雷達測距誤差為

式中：為光速；為毫米波波長；為雷達天線波束主軸與目標間的夾角。

自適應巡航控制系統根據毫米波雷達等傳感器觀測的信息控制車輛加速或減速。

在強降雨場景下，測量車距為

式中為自車與前車的實際車距。

強降雨場景下毫米波雷達測量車距與期望車距的車距誤差Δ為

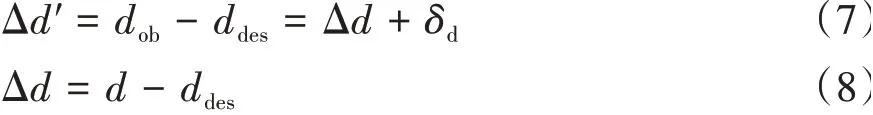
式中：Δ為實際車距誤差；為期望車距。

對于自適應巡航控制系統，控制目標為使自車與前車的實際車距趨近于期望車距，即要求車距誤差Δ趨近于零。強降雨場景下測量車距誤差Δ與實際車距誤差Δ的誤差可能會觸發ACC系統速度控制性能受限，引發非預期加速或減速，導致無法實現穩定跟車、與前車或后車發生碰撞。

2 強降雨場景下安全控制策略設計

強降雨場景下毫米波雷達的安全控制策略架構如圖1 所示，分為安全風險識別和安全控制兩個部分。使用雙狀態檢驗進行風險信息的識別，使用基于卡爾曼濾波的修正策略對安全風險進行修正，進而將修正后的信息引入ACC 控制器進行安全控制。

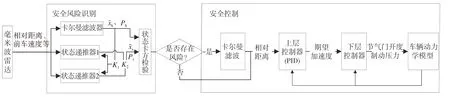
圖1 安全控制策略原理圖

2.1 基于雙狀態卡方檢驗的安全風險識別策略設計

強降雨場景中，毫米波雷達傳播衰減、信噪比降低，會造成目標運動信息測量誤差增大，使用雙狀態檢驗識別毫米波雷達中出現大量噪聲的情況。

定義狀態向量來表征前方物體的運動狀態：

式中：表示目標相對于自車的縱向位置；˙表示目標車輛相對于自車的縱向速度；表示相對加速度；表示相對加速度的導數。

前方目標運動狀態的狀態方程的連續時間模型表示為

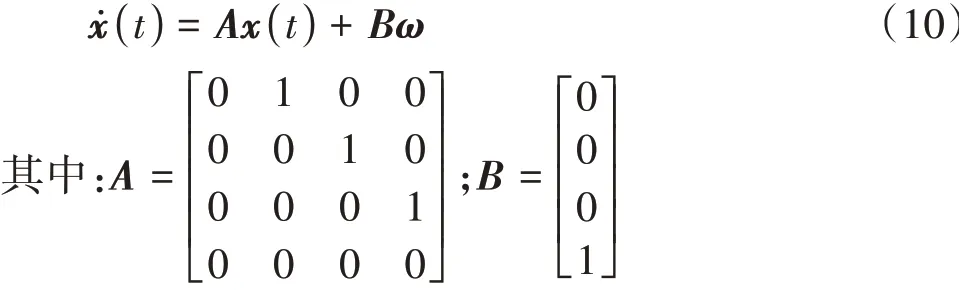
式中：為連續系統矩陣；為連續系統噪聲驅動矩陣；為過程噪聲，是相對加速度的導數的干擾。

通過線性離散化，前方目標運動狀態的狀態方程的離散時間模型為

式中：為系統狀態轉移矩陣；為系統噪聲系數矩陣；為系統采樣時間；()為時刻的狀態向量。一步預測狀態量^(+ 1|)通過上述狀態方程求得。

前方目標運動狀態觀測方程的離散時間模型表示為

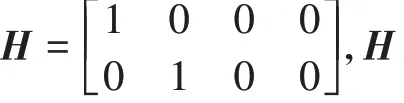
卡爾曼濾波的一步預測協方差(+ 1|) 為

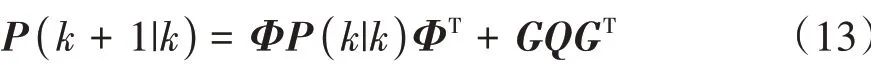
式中是過程噪聲的方差。

最終卡爾曼濾波器的狀態更新為

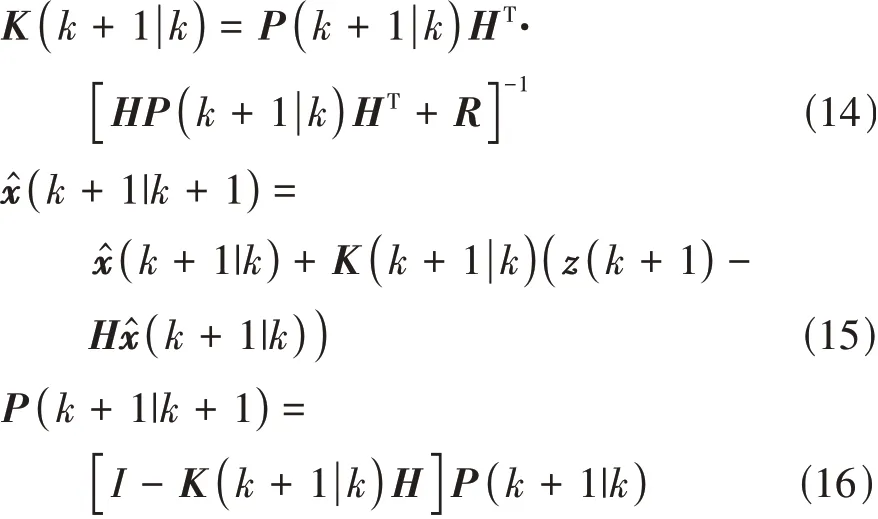
式中是測量噪聲的方差。

卡爾曼濾波的狀態估計值^(|)由一步預測信息^(|- 1)和實際觀測信息()融合得到，當系統存在功能不足、實際觀測信息存在風險時，狀態估計值^(|)也會包含風險信息。設計由先驗信息遞推得到的狀態遞推器，最終根據卡爾曼濾波狀態估計值^(|)與狀態遞推器^()的差值判斷是否存在風險信息。由卡爾曼濾波得到^ ()后，狀態遞推器進行狀態估計和方差遞推過程：

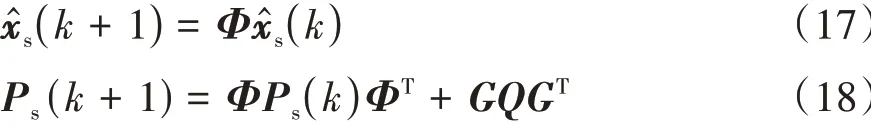
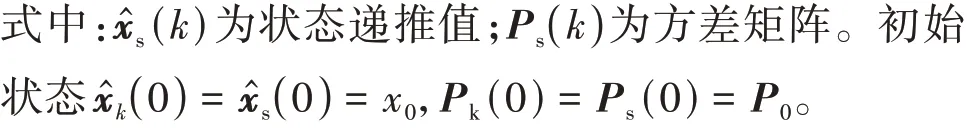
根據狀態濾波值^ ()和^()的差值可以判斷系統是否發生風險。

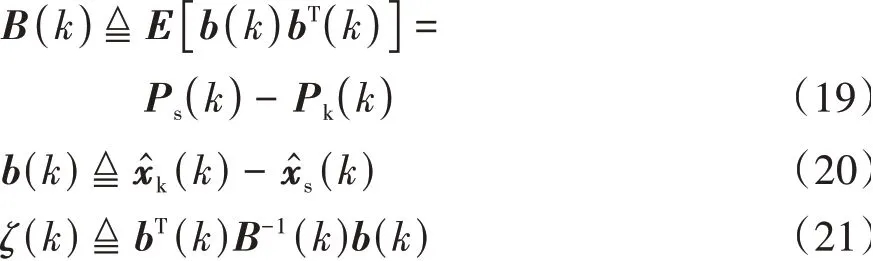
式中：差異向量()是零均值的高斯隨機向量；()是()的協方差；隨機狀態量() ～()。毫米波雷達是否存在風險的判斷準則為

式中是設定的檢測閾值，決定檢測的性能，由皮爾遜準則確定。

狀態遞推器的遞推值會隨著時間的累積越來越偏離真實值，導致遞推器失效，可以使用卡爾曼濾波的狀態估計值定期對狀態遞推值進行更新。但是當發生風險時，卡爾曼濾波的狀態估計值已經包含了風險信息，會污染狀態遞推器，導致無法檢測出信號異常現象。為了減小被污染的可能，提高安全風險識別的可靠性，可以設置兩個狀態遞推器，進行交替重置，當一個狀態遞推器被重置時，另外一個可以作為參考系統。

雙狀態卡方檢驗遞推器的重置和使用時間如圖2所示，在時刻系統信號出現了明顯的異常，存在風險。

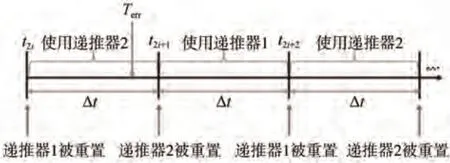
圖2 雙狀態卡方檢驗遞推器的重置和使用時間

設發生在時間區間(，)內，在時刻狀態遞推器1 已經被重置，在時刻狀態遞推器2即將被重置污染，在時刻狀態遞推器1 即將被重置污染，所以需要在時刻前檢測出信號異常。設?為從時刻到信號異常被檢測出來的時間間隔，?為雙狀態卡方檢驗遞推器的重置時間間隔。需要在(，)時間內檢測出信號異常，所以有

即雙狀態卡方檢驗遞推器的重置時間間隔大于信號異常的檢測時間。若重置時間過短，即遞推器被快速重置，可能在檢測到信號異常信息之前已經被污染，造成漏檢，無法有效進行安全風險識別；若重置時間過長，即遞推器重置速度比較慢，靈敏度會降低，誤差隨著時間不斷積累，等效為單卡方檢驗，容易造成虛警。雙狀態卡方檢驗算法流程圖如圖3所示。

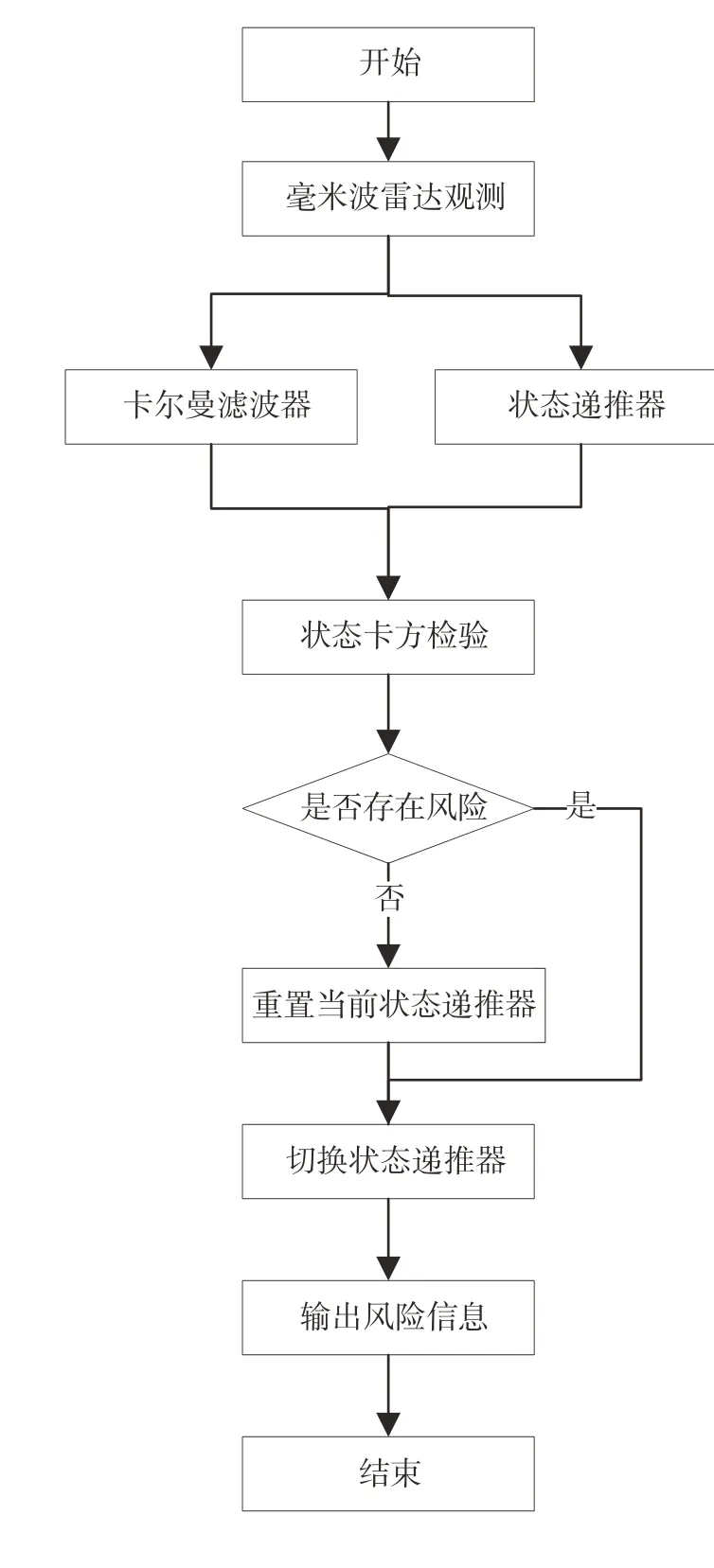
圖3 安全風險識別策略流程圖

2.2 基于卡爾曼濾波的安全控制策略設計

基于卡爾曼濾波的安全控制策略如圖4 所示，如果上文所述的安全風險識別策略識別到系統存在安全風險，就使用卡爾曼濾波進行信息修正。毫米波雷達觀測的運動信息經過修正之后，將修正信息輸入到ACC 的上層控制器當中，上層控制器為PID控制。

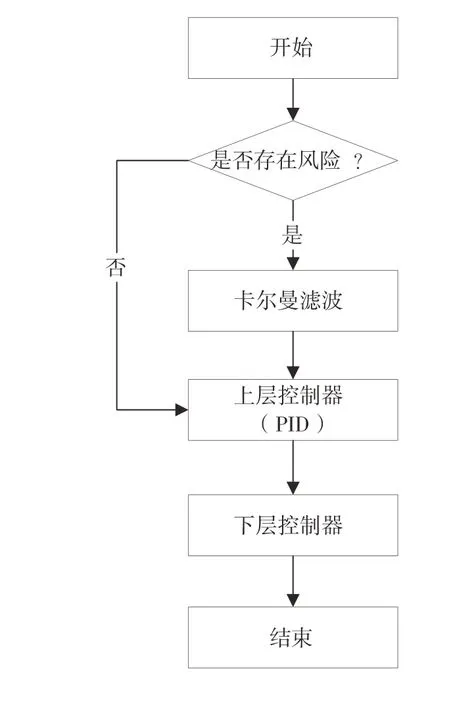
圖4 安全控制策略流程圖

式中：為設定的期望車距；()為時刻自車與前車的實際車距；Δ()為時刻的期望車距與實際車距之差。關于距離控制的PID 控制器的控制函數可以寫為

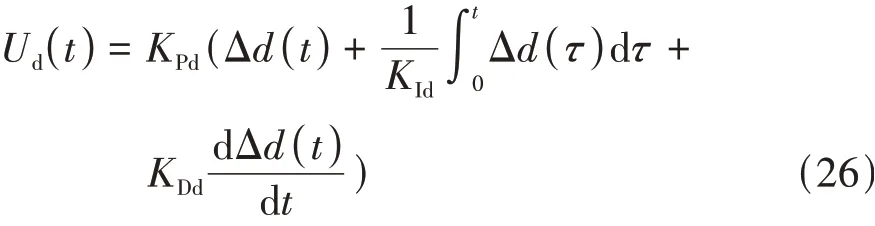
式中：為比例系數；為積分系數；為微分系數。假設區間為等份，每一份長度為，則上式離散化可得：

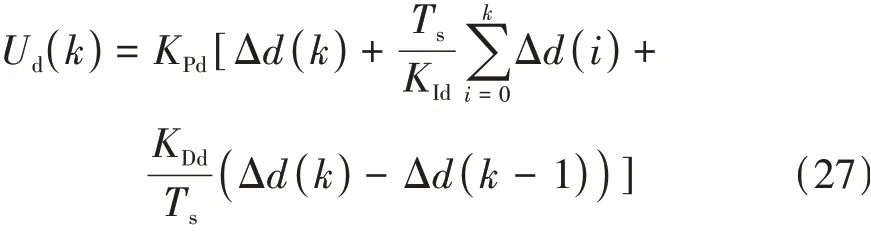
令=()，為期望加速度，是上層控制器的輸出信號。下層控制器對輸出信號進行處理，若為負值，則將輸出信號轉化為制動信號，若為正值，則將輸出信號轉化為驅動信號。

3 仿真驗證

搭建Prescan/Simulink 聯合仿真平臺，通過在仿真過程中的毫米波雷達測量信息中人為添加噪聲，模擬強降雨場景（圖5），驗證安全控制策略（圖6）的有效性。

圖5 仿真場景示意圖

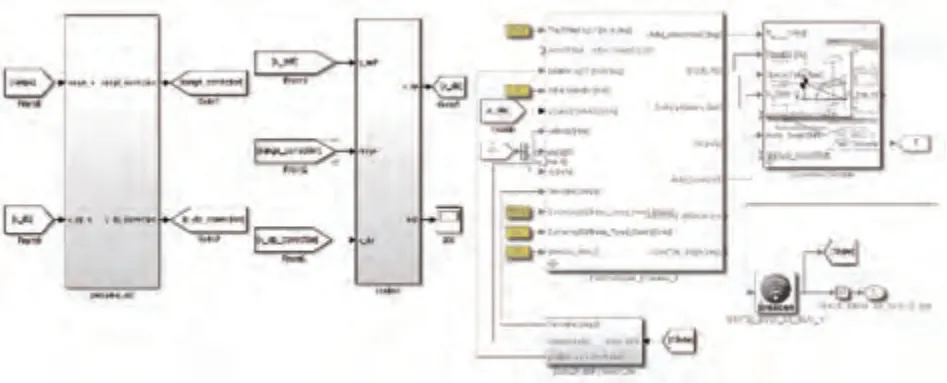
圖6 安全控制策略模型

3.1 仿真設計

在ACC 控制器前增加安全風險信息識別與修正模塊，ACC 控制器分為上層控制器和下層控制器兩個部分。

目前大多數在降雨場景下模擬毫米波雷達測量結果都是在理想結果輸出的基礎上添加噪聲來實現，這種模擬方式往往不能反映降雨對毫米波雷達的影響。為解決此問題，Hasirlioglu等建立了基于物理的虛擬降雨模型，使用Mie 理論和雷達方程分析降雨帶來的衰減和雜波的影響，模擬了降雨場景下毫米波雷達的目標返回功率和雜波功率的變化，與實車試驗結果吻合度較高。因此，在本文設計仿真工況時，首先使用Hasirlioglu 等建立的基于物理的虛擬降雨模型計算強降雨場景下毫米波雷達目標返回功率和雜波功率，再結合式（1）～式（3）計算出毫米波雷達的測量誤差，最后將測量誤差添加到毫米波雷達測量信息中。

參照氣象學中認為降雨量大于8.1 mm/h 為大雨或暴雨，因此設置強降雨的降雨量為10 mm/h，其他仿真參數如表1所示。

表1 仿真參數設置

最終計算得到毫米波雷達接受功率信噪比SNIR為20，距離測量誤差為2.91 m。根據距離測量誤差結果，設置噪聲注入毫米波雷達最終的輸出結果中模擬強降雨造成的影響。

設置勻速、勻加速、勻減速和復雜變速4 種不同的前車車速，編號分別為1、2、3、4，如圖7～圖10所示。

圖7 前車速度1

圖8 前車速度2

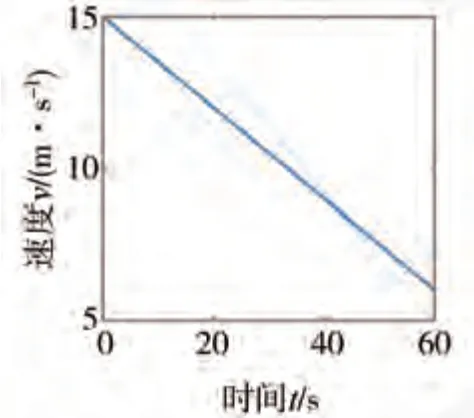
圖9 前車速度3

圖10 前車速度4

設置穿過雨區和持續降雨兩種降雨情況，最終設置不同的仿真工況，如表2所示。

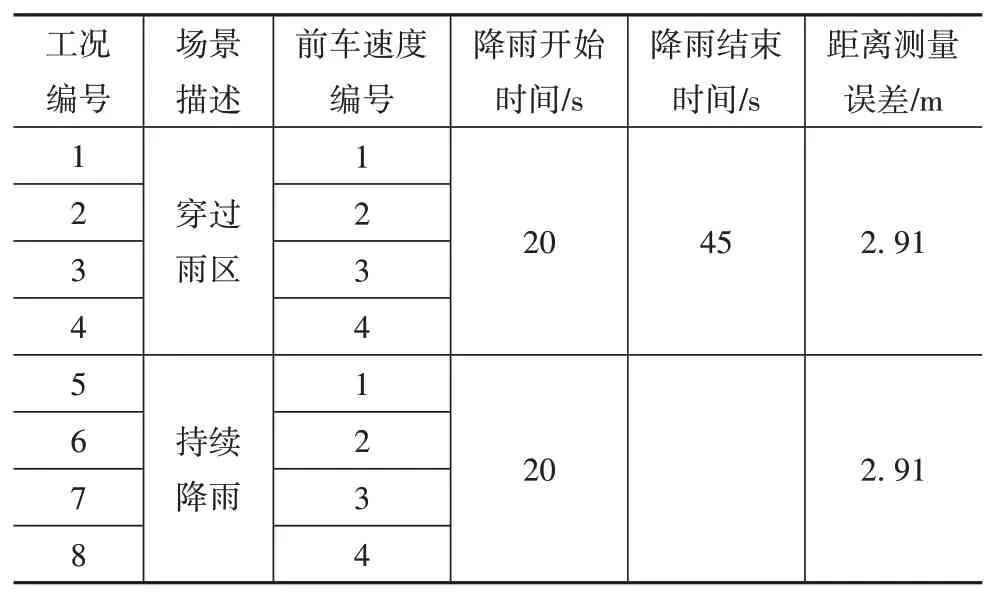
表2 仿真工況設計

3.2 仿真結果分析

根據表2 設計的仿真工況，得到各個場景的仿真結果，如表3 所示。風險時間表示在仿真場景中模擬強降雨的時間，檢測時間表示安全風險識別策略檢測到的ACC 系統存在SOTIF 風險的時間，檢測時間偏差表示風險時間和檢測時間之間的誤差。真實距離表示有安全控制策略情況下自車與前車的實際距離，修正距離表示有安全控制策略情況下卡爾曼濾波的修正距離。修正誤差表示最大的卡爾曼濾波修正距離與真實距離的誤差。

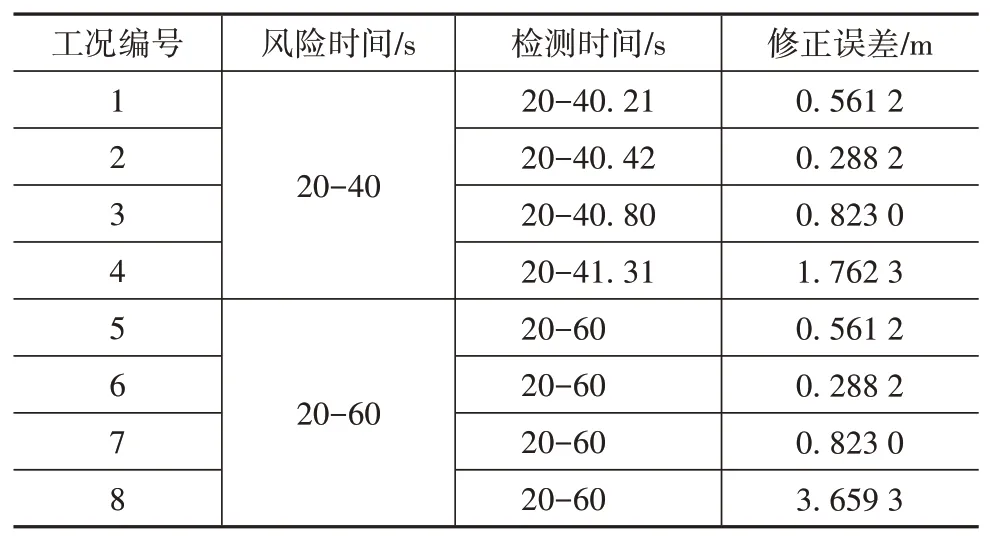
表3 仿真結果

如表3 所示，所提基于雙狀態的安全風險識別策略能夠及時有效地識別毫米波雷達測量的運動信息非預期誤差導致ACC系統性能局限的SOTIF風險，檢測時間偏差在1.31 s以內（工況4：檢測時間為20-41.31 s，風險時間為20-40 s）；實施安全控制策略后，卡爾曼濾波修正信息與真實數據之間的偏差在3.66 m 以內，ACC 系統可以穩定運行。無安全控制策略時，ACC系統無法穩定運行，自車可能與前車或后車發生碰撞。

工況4（20-40 s穿過雨區、大雨、前車復雜變速）的仿真結果如圖11～圖14 所示。flag-err 表示風險識別結果，當flag-err=0 時，安全風險識別策略認為系統無風險；當flag-err=1 時，安全風險識別策略認為系統存在風險。

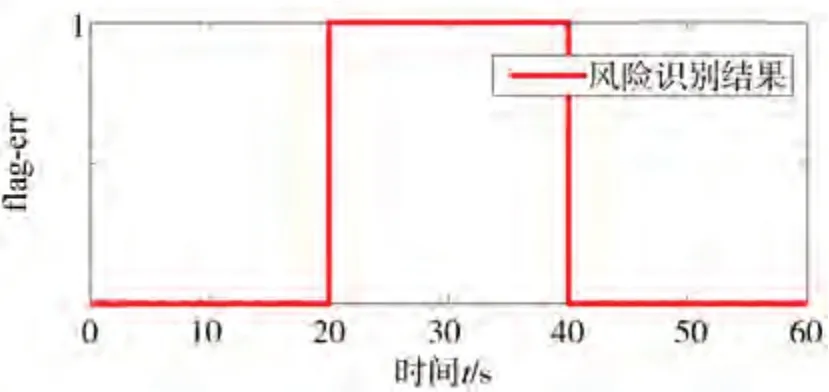
圖11 安全風險識別結果

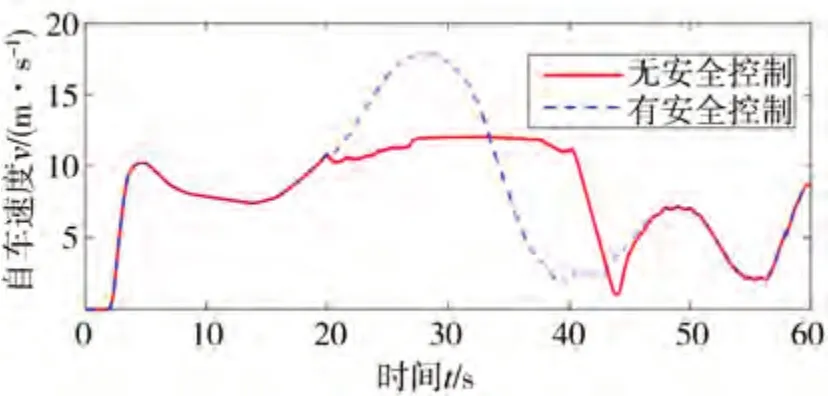
圖14 有安全控制和無安全控制時自車速度

由圖11可見，所提基于雙狀態的安全風險識別策略能夠成功檢測安全風險，即在20-40 s之間穿過強降雨區時毫米波雷達感知的運動信息存在非預期誤差，進而觸發ACC系統性能局限的SOTIF風險。圖12 表示實施安全控制之后的修正距離與真實距離，修正距離與真實距離最大相差1.76 m，真實距離與修正距離差距較小，修正距離合理可信。圖13和圖14 表示有安全控制和無安全控制時距離和速度的變化。在無安全控制策略時，從20 s 開始進入雨區，毫米波雷達測量的運動信息誤差較大導致ACC 系統存在SOTIF 風險。自車與前車之間距離增大，自車速度增加但此時的加速度較小，無法實現跟車；在26.75 s 時，前車與自車距離超出毫米波雷達最大檢測距離，自車以當前車速保持定速巡航狀態行駛，37.78 s 時，毫米波雷達再次探測到前車，系統切換為跟車狀態，自車與前車之間距離減小，自車速度減小，但此時的減速度較小，自車與前車距離持續減小，40 s 后風險結束，自車逐漸實現穩定跟車。在有安全控制策略時，自車可以保持穩定跟車行駛，驗證了安全控制策略的有效性。

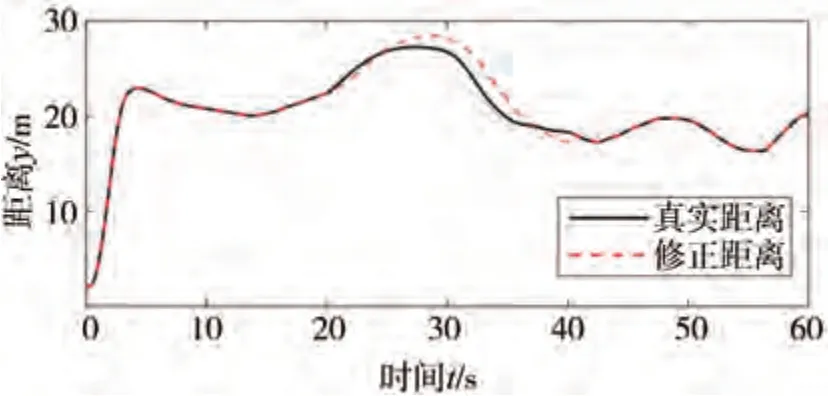
圖12 安全控制之后修正距離與真實距離

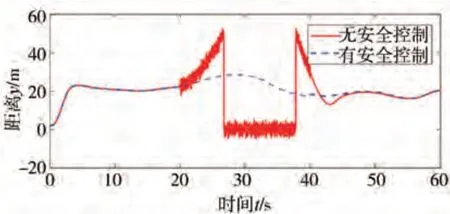
圖13 有安全控制和無安全控制時距離

工況8（20 s 開始持續降雨、大雨、前車復雜變速）的仿真結果如圖15～圖18所示。

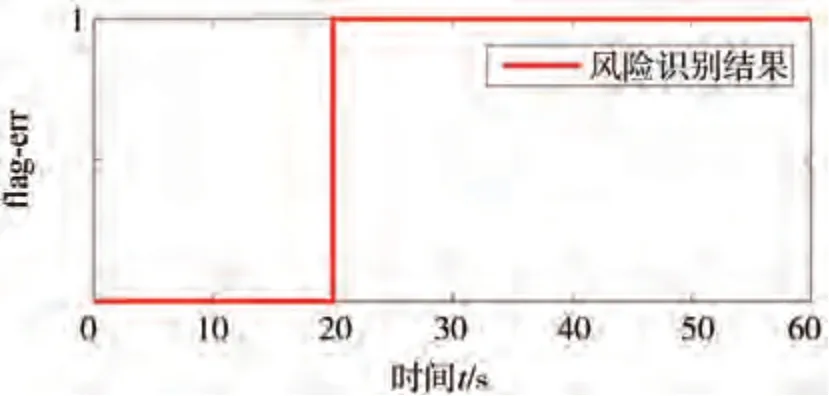
圖15 安全風險識別結果

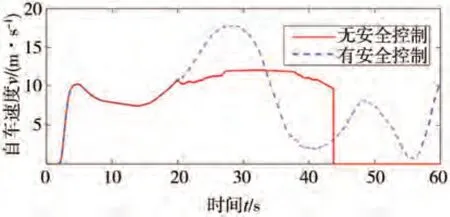
圖18 有安全控制和無安全控制時自車速度

由圖15可見，所提基于雙狀態的安全風險識別策略能夠成功檢測安全風險，即在20-60 s之間持續強降雨時毫米波雷達感知的運動信息存在非預期誤差，進而觸發ACC 系統性能局限的SOTIF 風險。圖16 表示實施安全控制之后的修正距離與真實距離，修正距離與真實距離最大相差3.66 m。此時降雨量較大且持續時間比較長，卡爾曼濾波修正距離和真實距離誤差增大；前車速度變化復雜，設定車距與實際車距之間的誤差增大，跟車效果變差，限制了安全控制策略的效果，最終的修正誤差較大。但是經過修正之后觀測距離變化幅度較小（如圖16 所示），ACC 系統可以穩定運行。圖17 和圖18 表示有安全控制和無安全控制時距離和速度的變化。在無安全控制策略時，從20 s開始持續降雨，毫米波雷達測量的運動信息誤差較大導致ACC 系統存在SOTIF風險。自車與前車之間距離增大，自車速度增加但此時的加速度較小，無法實現跟車；在26.75 s時，前車與自車距離超出毫米波雷達最大檢測距離，自車以當前車速保持定速巡航狀態行駛，37.78 s 時，毫米波雷達再次探測到前車，系統切換為跟車狀態，自車與前車之間距離減小，自車速度減小，但此時的減速度較小，減速不及時導致與前車在43.73 s發生碰撞。在有安全控制策略時，自車可以保持穩定跟車行駛，驗證了安全控制策略的有效性。

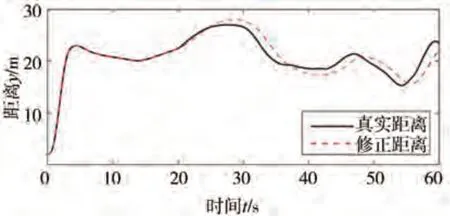
圖16 安全控制之后修正距離與真實距離

圖17 有安全控制和無安全控制時距離

同時，由表3 可知，在仿真工況1-3 和5-7 前車速度規律變化情況下，所提方法均能夠實現對非預期風險的及時識別，且工況1-3 穿過雨區后存在不超過1s 的虛警時間。卡爾曼濾波修正信息與真實數據之間的偏差在0.9 m 以內，可以實現穩定跟車行駛。

仿真工況4 為設定的穿過雨區、復雜變速工況。所提風險識別策略仍然可以實現對非預期風險的及時識別，但是由表3 可知，穿過雨區后虛警時間為1.31 s，與工況1-3相比，虛警時間變長，且修正誤差增加為1.76 m。虛警時間仍然在可接受范圍內，可以保證風險識別效果。雖然修正誤差較大，但是安全控制策略仍然可以實現穩定跟車行駛，如圖14 所示。仿真工況8 為設定的持續降雨、復雜變速工況。所提風險識別策略仍然可以實現對非預期風險的及時識別。仿真工況8 的修正誤差為3.66 m，修正誤差較大，但是安全控制策略仍然可以實現穩定跟車行駛，如圖18所示。

因此，前車車速影響風險識別策略和風險降低策略。前車車速變化復雜會使風險結束后虛警時間變長，但是虛警時間仍然在可接受范圍內，可以保證風險識別效果。前車車速變化復雜造成修正誤差增大，但是安全控制策略仍然可以實現穩定跟車行駛。

4 結論

針對強降雨場景下毫米波雷達感知的運動信息存在非預期誤差可能觸發自適應巡航控制系統性能局限的SOTIF 問題，本文中提出了一種安全控制策略。使用雙狀態檢驗實時對毫米波雷達的測量信息進行安全風險檢驗，將毫米波雷達觀測信息輸入到卡爾曼濾波器和兩個狀態遞推器當中，通過比較卡爾曼濾波器和狀態遞推器的差值判斷系統是否存在安全風險。識別到系統存在風險時，使用卡爾曼濾波對毫米波雷達觀測信息進行修正，將修正后的信息輸入ACC 上層控制器，基于PID 控制得到期望加速度輸入下層控制器，下層控制器將期望加速度轉化為驅動信號或制動信號對車輛進行控制。通過搭建的Prescan/Simulink 聯合仿真平臺對安全控制策略進行仿真驗證，仿真驗證結果表明：所提強降雨場景下自適應巡航控制系統安全控制策略能夠實時檢測由于強降雨導致的SOTIF 風險，并能夠實時修正非預期測量誤差，距離修正誤差在3.66 m 以內，有效保證了ACC 系統在強降雨場景下安全穩定運行。