基于AFSA-RF的兩相流型圖擴展技術

李旭鵬，鐘文義，喬守旭,*，譚思超，王庶光

(1.哈爾濱工程大學 黑龍江省核動力裝置性能與設備重點實驗室，黑龍江 哈爾濱 150001；2.哈爾濱工程大學 核安全與先進核能技術工信部重點實驗室，黑龍江 哈爾濱 150001)

氣液兩相流的流型是化工、石油以及火力、核能發電等行業生產過程中的一個重要參數[1-2]，對流型的精準預測對于生產應用有著重要意義。當今的流型識別，主要依靠可視化技術得到的圖像和電導探針、電阻式空隙儀所得到的水力特性來進行研究[3-5]。這些實驗研究對于兩相流特性有較好引導作用，但此類流型識別的方法主要以可視化方法為主，具有一定主觀性。實驗中所得到的兩相流型圖為經驗流型圖[6]，其水和空氣的表觀流速均處于低流速區(0～4 m/s)，無法滿足實際生產應用。

為解決上述流型識別研究中的問題，隨著近年來機器學習的快速發展，諸多國內外學者建立了基于人工神經網絡的兩相流流型軟測量模型，并取得了較好效果[7-10]。但神經網絡模型有以下幾個缺點[11]：1) 收斂速度慢，需要大量的時間成本與算力；2) 需要大量特征量來訓練以防止過擬合，兩相流的特征較為難取；3) 需要較龐大的訓練集進行訓練以保證預測精度，而大多數情況下仍以開展小批量實驗為主，獲得樣本數據較少，使得其工程應用較為困難。對于少樣本、少特征條件下分類，適用的模型組要有支持向量機(support vector machine, SVM)、K近鄰算法(K-nearest neighbor, KNN)和決策樹(decision tree, DT)3種。這3種模型的識別效果均優于人工神經網絡，其中屬SVM的預測精度最佳[12]。然而單一的簡單分類器精度無法超越集成學習模型(ensemble learning, EM)[13]，其中以決策樹為基分類器的隨機森林(random forest, RF)算法可以滿足精度要求。

RF是Bagging集成方法中最具有代表性的算法[14]，通過集成每棵樹的分類結果進行投票最終得出分類結果。近十幾年來，RF算法在各領域均得到了飛速發展，在生物學、信息技術、地理地質及經濟管理等領域中均有廣泛應用[15-19]。

人工魚群算法(artificial fish swarms algorithm, AFSA)[20]是一種新型的優化算法，該算法利用了魚的聚群、覓食和追尾這3個基本行為，采用自上而下的尋優模式從構造個體的底層行為開始，通過魚群中各個體的局部尋優，達到全局最優值在群體中凸顯出來的目的。

本文提出一種利用基于AFSA優化RF的優化識別模型，用以開展豎直下降兩相流流型的精準預測。通過對流量計所獲得的氣液兩相流速、雷諾數、施密特數以及處理后特征數進行訓練，實現對實驗較難達到的高流速區進行預測。

1 實驗研究

本實驗使用空氣-水兩相流，在室溫20 ℃、標準大氣壓下展開。如圖1[5]所示，實驗系統主要由空氣壓縮機、氣相回路、離心泵、水箱、液相回路、兩相混合腔、氣水分離器、實驗本體和測量系統所組成。其中，水箱容量為1 m3，兩相混合腔為雙環空腔結構的兩相注入系統，實驗管道內徑為50.8 mm，測試段長徑比為66，氣流量由轉子流量計測量，精度為±3%，水流量通過電磁流量計測量，精度為±5%。實驗中，氣相表觀速度(jg)為0.01～4 m/s，液相表觀速度(jf)為0.2～4 m/s。

圖1 實驗系統示意圖Fig.1 Schematic diagram of test facility

實驗過程中，空氣先通過氣體壓縮機壓縮至0.7 MPa，然后引至實驗本體頂部的兩相混合腔與引自水箱的去離子水混合，最終進入實驗本體實現自上而下的流動。在經過試驗段后，進入氣水分離器，經過分離后的氣體直接釋放到外部環境，去離子水則通過水管回路返回水箱。

圖2 豎直下降兩相流流型 Fig.2 Two-phase flow regime in vertical-downward tube

圖2為作者研究所獲得的豎直下降兩相流流型，主要分為泡狀流、彈狀流、攪混流和環狀流4種典型流型[5]。其中，泡狀流的氣泡大小均勻，呈橢球狀或球狀，分散于連續液相中。彈狀流中有細長的氣彈跟隨在液彈的下游，這些氣彈通常有一個偏心的頭部，指向與流動方向相反的方向，并且它們的弦長大于管道直徑。在尾部附近，小氣泡從邊緣被剪切掉，形成尾流區。攪混流中，高度扭曲的氣段塞占據了整個管徑，而連續的氣段塞之間存在著高度混亂的液塞，在壁面附近形成了攜帶小氣泡的波狀液膜；此外，在尾流區還存在逆流現象。環狀流中，連續氣相夾帶液滴在管道中心流動，壁面附著有一層連續且呈波浪狀液膜。

對實驗所選工況的流型繪制流型圖及流型轉換邊界，如圖3所示。從圖3可看出，不同流型之間有著高度的非線性可分特性。

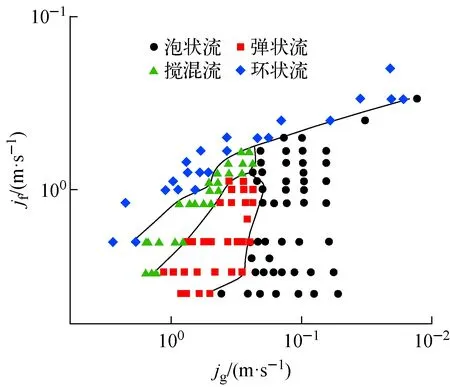
圖3 流型與轉換邊界Fig.3 Flow pattern and conversion boundary

2 模型建立

2.1 RF分類

RF算法[14]在以決策樹(decision tree, DT)為基學習器構建Bagging[21]集成的基礎上，進一步在決策樹的訓練過程中引入隨機屬性的選擇。該分類模型的原理是利用與決策樹相同的樹狀結構，將數據記錄進行分類，樹的1個葉結點即代表某個條件下的1個記錄集，根據記錄字段的不同取值建立樹的分支[22]。

對機器學習中的決策樹而言，如果帶分類的事物集合可劃分為多個類別中，則某個類(xi)的信息可定義如下:

I(X=xi)=-log2p(xi)

(1)

其中:I(X)為隨機變量的信息；p(xi)為xi發生時的概率。

為克服決策樹對樣本空間過度分割導致過擬合的問題，RF使用Bagging方法集成決策樹，通過對若干個單個的決策樹分類器經過特定的結合策略形成了1個強分類器模型。RF在訓練決策樹模型的過程中，增加了隨機屬性的選擇，經過n個決策樹訓練后，使每個分類結果進行投票決出最終類別。其絕對多數投票法的投票過程可如式(2)所示：

H(x)=

(2)

過擬合的主要原因是模型學習了太多樣本中的隨機誤差。因為RF隨機選擇了樣本和特征，并且將很多這樣的隨機樹進行了平均，這些隨機誤差也隨之被平均，乃至相互抵消。因此，RF有效防止了過擬合的問題，并能顯著提高分類精度。

2.2 流型圖擴展

實驗中所得到的兩相流型圖為經驗流型圖，其兩相流流速均處于低流速(0～4 m/s)區，無法滿足實際生產應用。RF可通過已有的數據對樣本集外的區域進行預測，實現流型圖的擴展。

對于這類樣本集外區域的特征，稱作超范圍特征，不同的超范圍特征所組成的情況稱為超范圍情況。對于流型圖這類的二維圖表主要有單一特征擴展以及多特征擴展，需對原本不需劃分訓練集和測試集的數據進行分類。

圖4 超范圍特征Fig.4 Classification of beyond condition case

如圖4所示，本文將特征值高區作為未知的空白區域測試集，然后進行訓練與預測，這樣訓練的模型才能有效對超范圍特征預測，且可初步判斷流型圖擴展之后是否可靠，提高擴展后流型圖的準確率與可信度。

2.3 RF參數優化

由于需實現流型圖的擴展，RF分類算法默認的方式精度較低。除對其參數與訓練集進行一定的優化選取外，還需對其參數進行優化。

RF分類算法有兩個重要的參數：葉子數(MinLeaf)和樹數(nTree)，分別代表著葉子節點的最小樣本數目和指定RF中分類器的個數。傳統RF算法優化中大多使用窮舉法、網格搜索法和交叉驗證法。窮舉法和網格搜索法效率低下，而交叉驗證在小樣本情況下會過高估計參數值[23]。

利用AFSA尋找最佳MinLeaf、nTree以及訓練集與測試集劃分的RF分類模型主要流程如圖5所示。

圖5 AFSA-RF模型流程Fig.5 Process of AFSA-RF model

主要涉及以下步驟。1) 劃分集合：按照所需流型特征域與已有特征域關系依照超范圍特征分類法，隨機劃分訓練集和測試集。2) 種群初始化：隨機生成系列MinLeaf、nTree初始人工魚群。3) 人工魚覓食、群聚與追尾：人工魚隨機在范圍內選擇新的點進行覓食，如果滿足條件向其靠近1步，探索周圍鄰居魚的最優位置，當最優位置的目標函數值大于當前位置的目標函數值并且不是很擁擠，則當前位置向最優鄰居魚移動，否則繼續覓食。4) 選擇操作：若滿足人工魚群中止條件，輸出最佳MinLeaf、nTree參數組合，否則重新進行覓食、群聚與追尾行為直至找到最佳MinLeaf、nTree。5) 精度檢測：將最佳MinLeaf、nTree組合輸入RF模型進行測試，判斷是否滿足精度要求。6) 建立AFSA-RF模型：若符合精度要求，記錄最優MinLeaf、nTree參數和特征子集組合以完成模型建立并開展預測集分類預測。

3 模型訓練與結果討論

3.1 模型訓練

如圖6所示，采用2.2節所述超范圍情況選取法選取實驗工況145組，其中設置訓練集與測試集比例接近7∶3。訓練集中流型占比：泡狀流，38.6%；彈狀流，22.8%；攪混流，15.9%；環狀流，21.8%。測試集中流型占比：泡狀流，36.4%；彈狀流，22.8%；攪混流，18.2%；環狀流，22.8%。將jg、jf、雷諾數(Re)、施密特數(Sc)4個基本特征及其經過簡單計算處理所得的處理特征作為特征輸入，將流型標簽作為網絡輸出，其中，流型標簽為泡狀流、彈狀流、攪混流、環狀流。

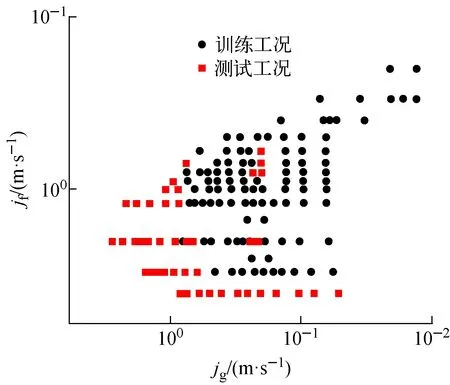
圖6 工況數據選取Fig.6 Working condition data selection

網絡訓練前，對數據初始化參數。設置MinLeaf、nTree的參數組合尋優范圍為[1，20]與[1，300]，生成魚群規模10，最多迭代次數300，最多試探次數10，感知距離1，擁擠度因子0.618，步長0.1。參數尋優過程中RF訓練目標準則設置為PRF_for_AF≥170，PRF_for_AF的表達式為：

(3)

(4)

其中：Ptrain為模型訓練的精度；Ptest為模型對超范圍特征區域預測精度；Pdifference為二者之差。該式既能要求兩個精度均達到較高水平，又可在保證不過擬合和欠擬合的情況下使對超范圍特征區域預測精度盡可能高，以達到對高流速區域精準預測。在滿足上述條件下，基于AFSA優化RF的袋外失誤率變化情況如圖7所示，隨著迭代次數的增加，袋外失誤率也逐漸減小并趨于范圍收斂，表明優化模型參數設置得當，訓練效果較好。此時最佳MinLeaf、nTree分別為9、83。此時，AFSA-RF模型針對當前特征子集的訓練精度和測試精度分別為93.07%和90.91%。

圖7 袋外失誤率Fig.7 Out of bag error

3.2 結果討論

RF模型中影響因子為袋外觀測置換變量增量錯誤(OOBPermutedVarDeltaError)，其定義為均方誤差與標準差之比，其定義式為：

OOBPermutedVarDeltaError=

(5)

利用最佳MinLeaf、nTree和特征子集組合構建優化模型并實現預測集中流型分類，經過AFSA-RF模型訓練之后，如圖8所示，得出影響因子最大的3組特征值依次是氣/液流速之比、氣相流速和液相流速。流型圖繪制通常以氣相流速、液相流速為坐標，故本文選用氣、液表觀流速及氣液兩相流速比這3個特征作為特征輸入。

圖8 特征影響力排序Fig.8 Ranking of influence characteristic

通過訓練集數據構造的預測模型對所有原始數據的預測結果列于表1，其中錯誤流型全部位于流型轉換邊界線附近，本文認為造成這一現象的原因是轉換邊界處流型特征向量間區別較小，交叉重疊的雜糅信息過多。其中彈狀流的精度最低的原因主要是由于它與其他3種流型均有轉換邊界，容易使模型誤判。

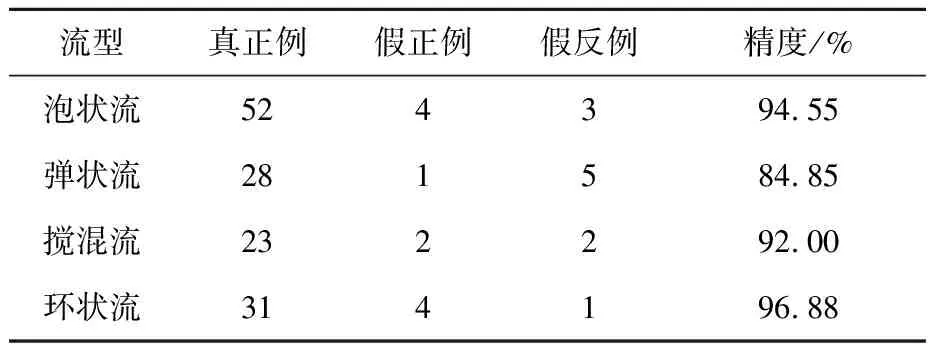
表1 原始數據預測結果Table 1 Forecast results of original data

通過按照2.2節與3.1節所述方法選擇的訓練集數據構造的低流速區域(jg≤2 m/s，jf≤4 m/s)預測模型所作的流型圖及其與實際流型對比如圖9所示。

通過全部數據構造的預測模型所作的低流速區域(jg≤2 m/s，jf≤4 m/s)和高流速區域(jg≤4 m/s，jf≤8 m/s)的流型圖分別如圖10a、b所示，從圖10c可知，使用訓練集數據得出的流型圖與使用所有數據得出的流型圖，僅因全部數據中多了一些轉換邊界附近的補充，使泡狀流-塞狀流轉換邊界有局部微調，但針對流速較高的部分，轉換邊界幾乎完全相同。這說明本文提出的流型圖擴展方法有效，可使用該方法進行高流速區域的流型預測并繪出流型圖。在此流速區域的兩相流體可通過直接讀圖或在已訓練好的AFSA-RF模型中輸入特征進行流型判斷。

圖9 訓練集數據構造流型圖Fig.9 Flow pattern graph by partial data

a——低流速區域流型圖；b——高流速區域流型圖；c——全部數據與訓練集數據模型對比圖圖10 全部數據構造流型圖Fig.10 Flow pattern graph by all data

重復計算10次后，經過優化后的RF模型的平均訓練精度與測試精度分別為91.08%和89.55%，未優化的RF模型的平均訓練精度與測試精度分別為77.20%和83.18%。由此可知，經過AFSA優化的RF模型訓練精度和測試精度均更高，且在實驗觀察中發現未經優化的RF模型在第1、7、9組出現了較嚴重的欠擬合現象，在第8組出現了過擬合現象，穩定性遠不如經過AFSA優化過后的RF預測模型。

為評估具體模型的有效性，在相同實驗工況的前提下，對比了窮舉法(enumeration method, EM)、交叉驗證法(cross-validation, CV)、網格搜索法(grid search, GS)和AFSA 4類優化方法對模型的預測效果的影響。如表2所列，4種模型的訓練與預測精度均在75%以上，但除了CV和AFSA-RF以外兩種基本模型的預測效果較差。且GS和CV進行流型判斷的模型，出現了較明顯的欠擬合現象，這是傳統參數優化方法的缺陷所在。EM雖然精度有了明顯提升，但相比AFSA還有一定差距。

更高的精度預測使AFSA-RF更適合用于流型的預測與高流速區域超范圍特征預測，獲得高流速區域的流型圖。但由于其設置了參數的目標準則來防止過擬合與欠擬合，而不是以完成次數或訓練經度為準則，整個模型的計算時間遠超過其他4種，高于最快的CV近55倍，故不適合直接作為在線預測模型，還需通過其他優化方法進行加速。

表2 不同優化模型流型預測結果對比Table 2 Results of different models

4 結論

本文通過豎直下降管內氣-水兩相流可視化實驗，提出了AFSA-RF用于兩相流流型圖自動生成，通過超范圍特征來劃分相應訓練集工況，將流型圖向外擴展，實現兩相流流型圖自動生成；通過設置參數目標準則防止過擬合和欠擬合行為的發生，保證了預測合理性和準確性；通過人工魚群加速獲得合理的參數組合得到了較其他優化模型更高的訓練精度與測試精度。