輪對空心軸雙級六連桿傳動系統剛度分析研究

楊勇軍，高 文，樊 平，張 健，魏春陽

（中車戚墅堰機車有限公司 產品設計部，江蘇 常州 213011）

隨著經濟和技術的發展，列車運行速度越來越高。作為發揮列車牽引動力的鐵路機車動力轉向架，其驅動系統技術也在不斷發展，以適應新的運用要求。對于最高運行速度160～200 km/h 的準高速機車轉向架，為減輕簧下質量以達到降低輪軌動作用力的目的，大多采用了輪對空心軸式架懸驅動系統技術，例如DF9、DF11等內燃機車，SS8、SS9等電力機車，以及近幾年研發的準高速交流傳動機車等。雖然這些機車上的驅動裝置具體結構有較大的差異，但輪對空心軸傳動機構的結構形式和原理是相同的。

在輪對空心軸式驅動裝置技術研究方面，業內技術人員主要開展了驅動裝置結構特點及強度、集成應用技術、牽引扭轉黏滑振動、驅動裝置動力學性能和整車動力學性能等方面的研究［1-4］。針對六連桿傳動系統自身剛度特性方面，封全保［5］對傳動系統剛度試驗方案進行了構思并作了試驗研究；鐘文生［6］從六連桿運動關系出發討論了橡膠關節徑向剛度特性對橫向運動的影響。而輪對空心軸傳動系統結構布置尺寸與傳動系統各向剛度之間內在規律的研究未見公開報道。為實現精益研發，有必要開展相關研究，一方面為新型輪對空心軸傳動系統的研發提供便捷手段，同時也為既有產品的結構優化研究提供理論支撐。

文中將輪對空心軸傳動機構作為研究對象，通過經典力學方法對輪對相對于電機的位移和受力情況進行分析，以期摸索出計算輪對空心軸傳動機構各向剛度的通用方法。

1 輪對空心軸傳動機構原理

1.1 傳動機構原理

以DF11機車為例，輪對空心軸架懸式驅動裝置由懸掛于轉向架上的牽引電動機、牽引齒輪副及齒輪箱、輪對及傳動系統組成。傳動系統的使用要求：在確保傳遞牽引電動機牽引扭矩這一功能的前提下，要具有靈活的變位能力，以避免機車動力學性能的惡化。為此，傳動系統采用了2 級結構類似的六連桿裝置，且每根連桿的兩端均裝有橡膠關節。牽引扭矩傳遞路徑如圖1 所示，電機輸出的扭矩經齒輪副傳遞到從動齒輪輻板后，通過齒輪級六連桿裝置傳遞到空心軸、車輪級六連桿裝置，最后傳遞到車輪上，從而實現輪對與鋼軌間黏著牽引力的發揮。

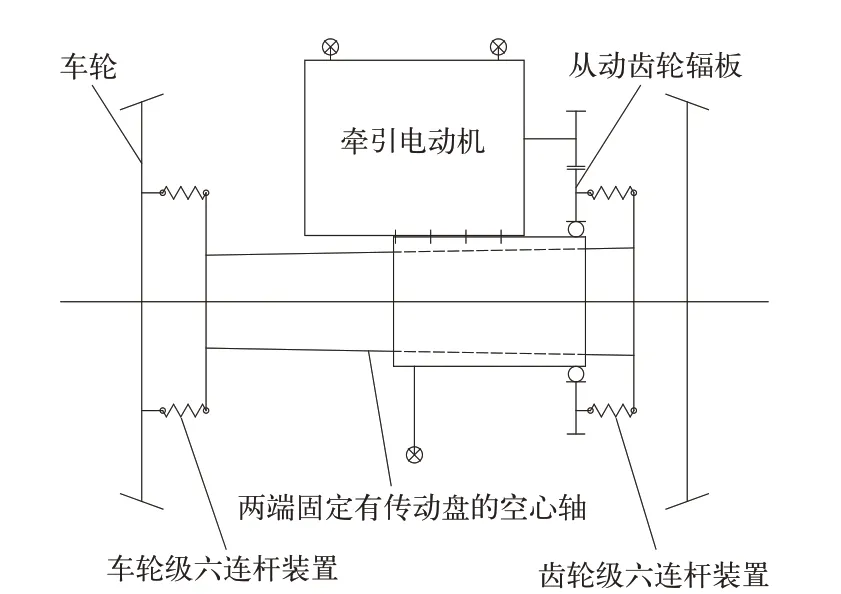
圖1 輪對空心軸傳動機構原理

對于此類型的驅動系統，從動齒輪除了可相對其軸線作回轉運動外，因受結構限制，在垂向、縱向和軸向這3 個方向上可看作與電機同步運動。因此，輪對相對于從動齒輪3 個方向的運動關系也就代表了輪對相對于電機的運動關系。故下文將輪對與從動齒輪之間承擔連接作用的空心軸及2級六連桿裝置作為分析對象進行受力分析，研究傳動系統的各向剛度特性，研究結果可用于評估由于輪對與電機之間相對位移而產生的作用力的大小。

1.2 六連桿布置特征

為保證傳遞扭矩時各連桿受力均勻，六連桿裝置的結構布置必須確保傳遞任一方向扭矩時，受拉與受壓的連桿各3 副互隔、且分別呈120°均布。以下稱這一特征為“六連桿均布”。“六連桿均布”的一個特例如圖2 所示，即受拉與受壓的連桿互隔且各連桿呈60°均布。

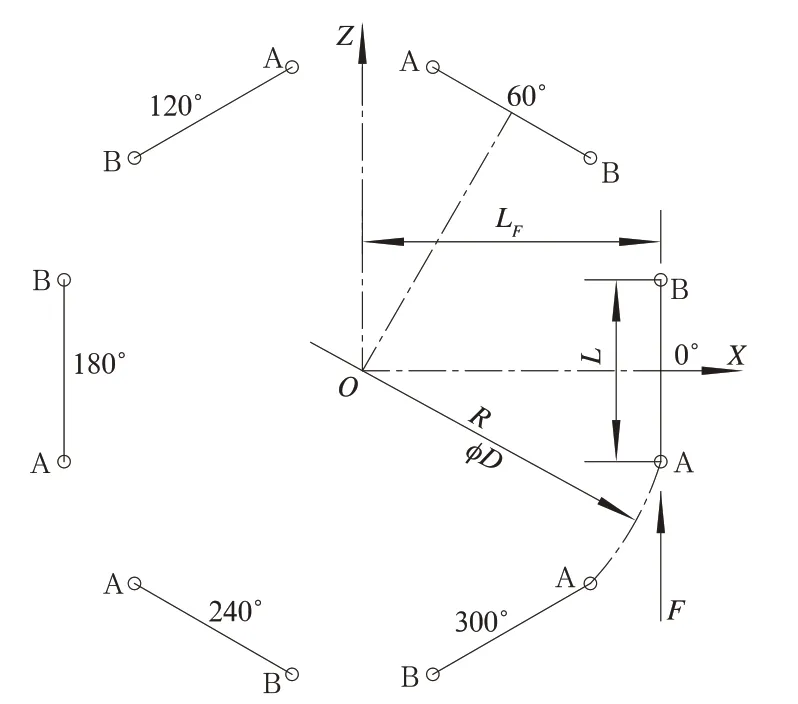
圖2 六連桿布置特征

2 連桿各向剛度分析

為方便敘述，文中所指連桿，均包含連桿及其兩端的橡膠關節。鑒于連桿是組成空心軸傳動機構的基本要素，在分析六連桿裝置各向剛度前，先對單一連桿的各向剛度特性進行分析。根據傳動機構的運動特點，為簡化分析過程，假定同一連桿兩端橡膠關節的芯軸始終保持平行；連桿體視為剛體；連桿兩端的橡膠關節各向剛度視為恒定值。

2.1 連桿長度方向拉壓剛度（縱向剛度）

連桿沿長度方向的拉壓剛度，由兩端橡膠關節的徑向剛度串聯構成，為式（1）：

式中：kr-link為連桿長度方向拉壓剛度，即連桿縱向剛度；kr為橡膠關節的徑向剛度。

2.2 連桿芯軸方向平動剛度（橫向剛度）

連桿橫向剛度分析如圖3 所示，假設連桿A 端芯軸固定，在XOY平面內平行于芯軸方向（Y向）的力F作用下，B 端芯軸橫移至B’，且B’相對于B在X向允許位移。現分析B 端芯軸相對于A 端芯軸的橫向平動剛度。經分析，可得到式（2）～式（5）：

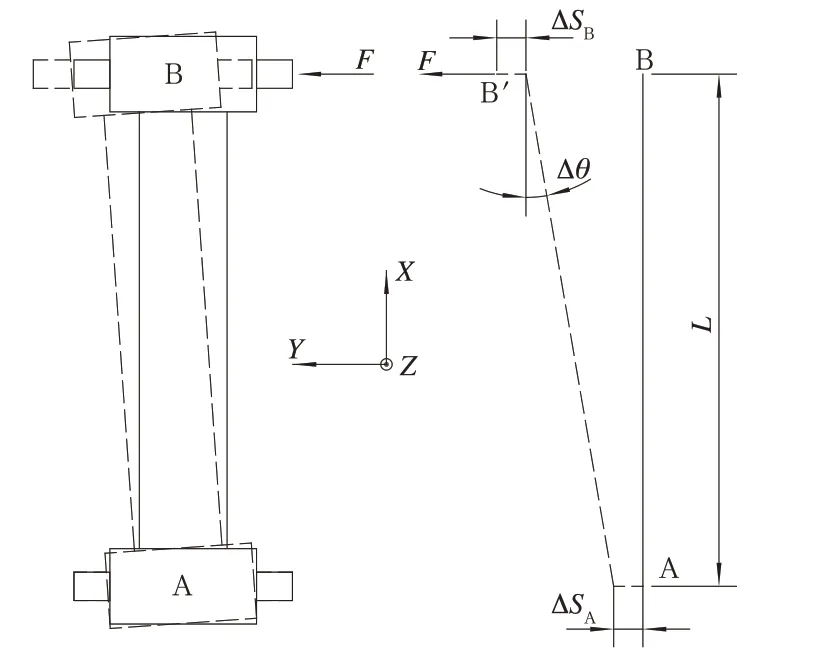
圖3 連桿橫向剛度分析

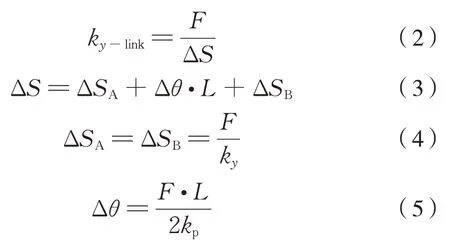
則有式（6）：

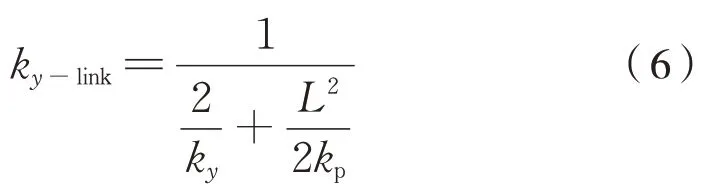
式中：ky-link為連桿一端芯軸相對于另一端在芯軸方向的平動剛度（一根連桿的橫向剛度）；L為連桿基準長度；ky、kp分別為橡膠關節的軸向剛度和偏轉角剛度。

2.3 連桿平動抗扭剛度

連桿平動抗扭剛度分析如圖4 所示，連桿A 端芯軸固定，在ZOX平面內沿芯軸寬度方向（圖中Z向）力F作用下，B 端芯軸受結構約束保持平行于A 端芯軸，兩芯軸由于相對于連桿體扭轉而形成在芯軸寬度方向（即Z向）的相對位移量ΔSt。現分析力F與位移量ΔSt之間的比例關系。

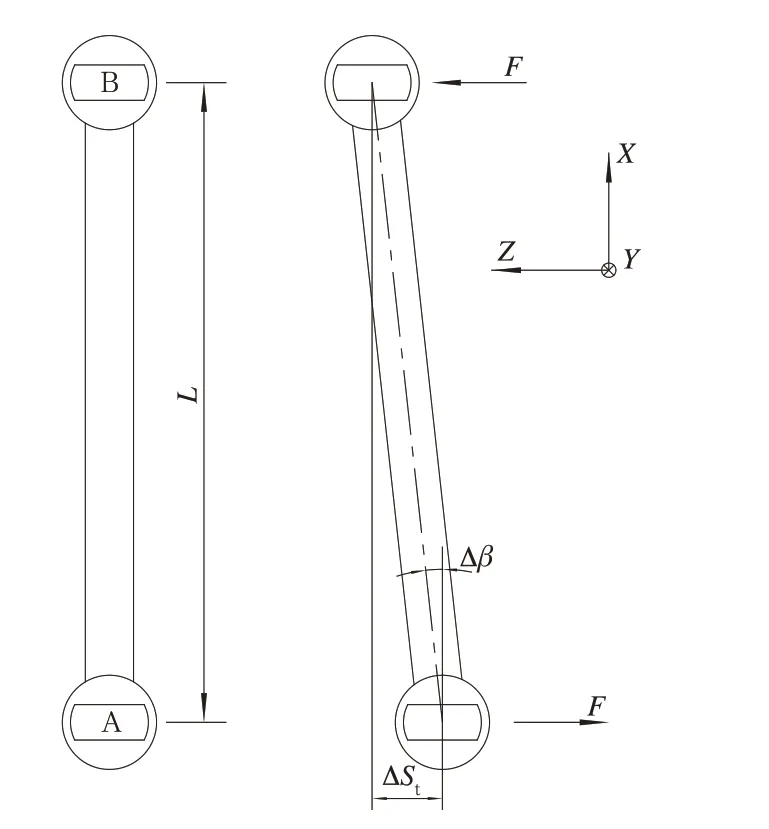
圖4 連桿平動抗扭剛度分析

設橡膠關節扭轉剛度為kt，則長度為L的連桿、在力F作用下，有式（7）：

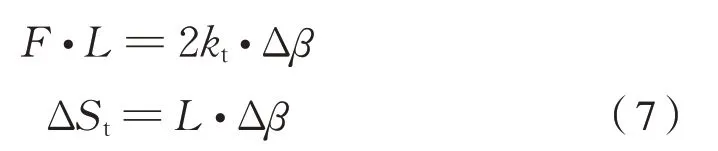
式（7）聯解可得兩橡膠關節扭轉剛度產生的連桿平動抗扭剛度計算為式（8）：

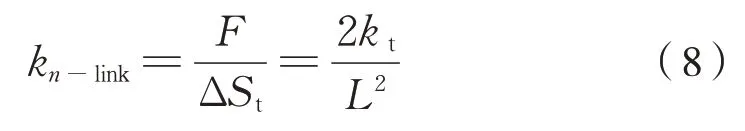
即式（9）：

式中：kn-link為連桿一端芯軸相對于另一端在芯軸寬度方向的平動剛度；kt為橡膠關節的扭轉角剛度。

2.4 θ 角體位連桿的兩端相對垂向平動剛度

假設一副呈任意θ角體位（以鉛垂方向為基準）的連桿，如圖5（a）所示，其芯軸A 固定，在垂向力F作用下，芯軸B 因受結構約束，其安裝面保持與芯軸A 平行，且只能在垂向產生位移。現分析垂向力F與兩芯軸之間垂向位移的比例關系。

作受力分析如圖5（b）所示，可得計算式（10）：

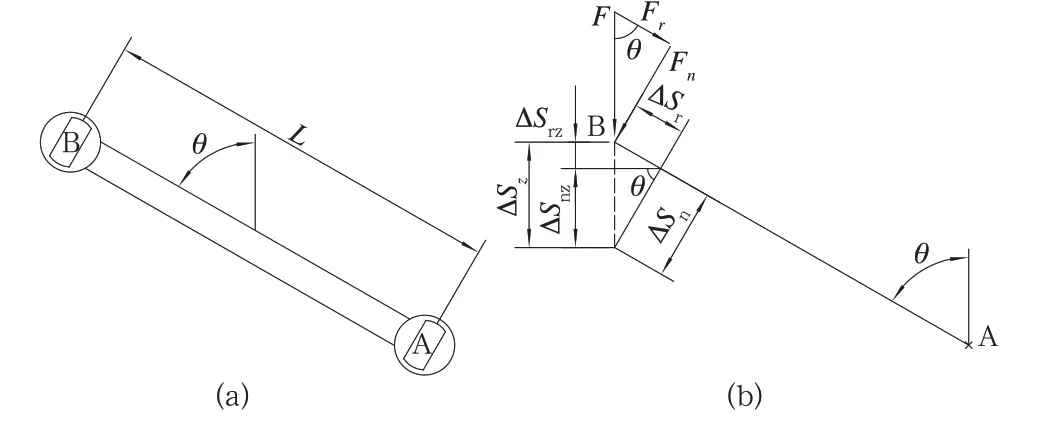
圖5 任意θ 角處連桿垂向平動受力分析

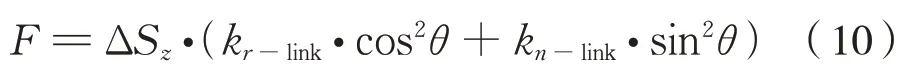
則θ角 體 位 連 桿 的 垂 向 平 動 剛 度kz，θ-link計 算公式為式（11）：

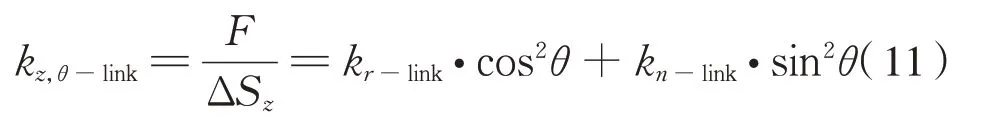
對于橡膠關節徑向剛度為kr、扭轉剛度為kt的連桿，將式（1）和式（9）代入上式，得到θ角體位連桿的垂向平動剛度計算公式為式（12）：

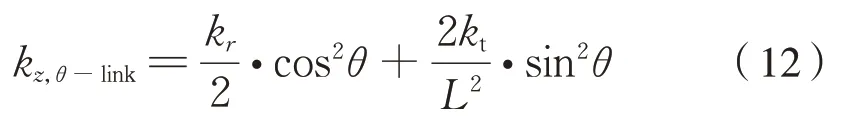
式中：kz，θ-link為θ角 體位 連 桿的 垂向 平動 剛 度；L為連桿基準長度；kr、kt分別為連桿橡膠關節的徑向剛度和扭轉剛度。

3 傳動機構各向剛度分析與計算公式推導

傳動機構指由車輪級和齒輪級具有“六連桿均布”特征的六連桿裝置及空心軸組成。

3.1 橫向剛度

考察六連桿裝置的橫向（即車軸方向）力傳遞過程可知，6 副連桿呈并聯作用，因此六連桿裝置的橫向合成剛度計算公式為式（13）：

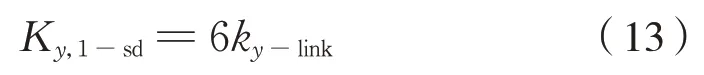
式中：Ky，1-sd為六連桿裝置的橫向合成剛度；ky-link為一根連桿的橫向剛度。

傳動機構的橫向剛度，由2 級六連桿裝置串聯構成，故傳動機構橫向剛度計算為式（14）：

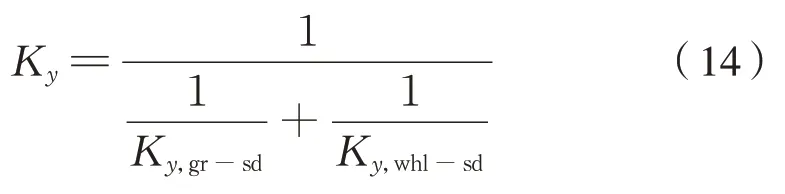
式中：Ky，gr-sd、Ky，whl-sd和Ky分 別為齒 輪級六 連 桿裝置的橫向合成剛度、車輪級六連桿裝置的橫向合成剛度和傳動機構總的橫向合成剛度。

3.2 牽引扭轉剛度

根據圖2，以齒輪級六連桿裝置為例進行扭矩傳遞過程中的受力分析。設連桿基準長度為L、兩端關節中心布置在半徑為R的圓周上，在傳遞扭矩6Mlink時，每根連桿傳遞的拉力或壓力均為F。則力F對圓心O 點的力臂長度LF及力矩Mlink為式（15）、式（16）：

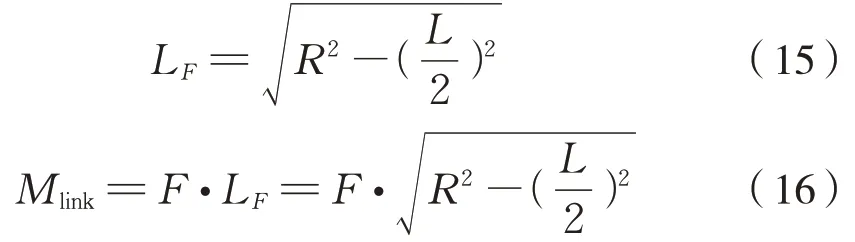
設六連桿裝置傳遞的總力矩為M1-sd、從動齒輪相對于空心軸（傳動盤）繞圓心O 點回轉角位移為Δβ1-sd，則M1-sd、Δβ1-sd及從動齒輪位于半徑LF處的切向位移Δr的計算式為式（17）、（18）、（19）：

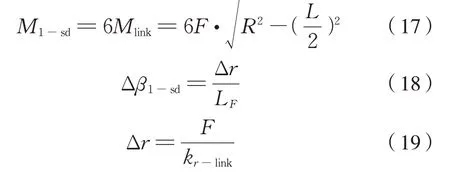
則六連桿裝置牽引扭轉剛度Kt，1-sd為式（20）：

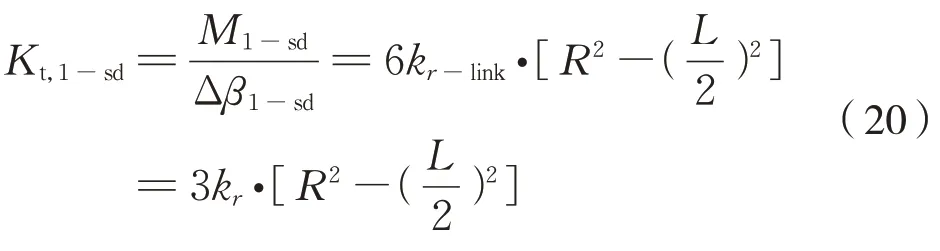
這就得到1 級六連桿裝置的合成牽引扭轉剛度為式（21）：

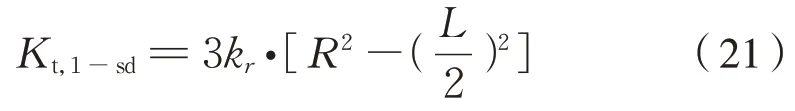
式 中：Kt，1-sd為 六 連 桿 裝 置 的 牽 引 扭 轉 剛 度；kr為橡膠關節徑向剛度；L、R分別為連桿基準長度和傳動銷定位圓半徑。

因此傳動機構的合成牽引扭轉剛度由2 級六連桿裝置串聯構成為式（22）：

式 中：Kt，gr-sd、Kt，whl-sd和Kt分 別 為 齒 輪 級 六 連 桿 裝置的扭轉剛度、車輪級六連桿裝置的扭轉剛度和傳動機構扭轉剛度。

3.3 垂向剛度

從動齒輪相對于車輪的垂向位移可看成是2級六連桿裝置的垂向平動位移與空心軸側滾位移相疊加而成。以下分別分析這2 種情況。

（1）考慮六連桿裝置垂向平動

前文已分析了處于任意θ角的連桿受力情況，得到了連桿兩端芯軸相對垂向平動時的剛度計算公式（12）。對于圖2 所示六連桿裝置，其垂向合成平動剛度只需將處于不同θ角的6 副連桿的垂向平動剛度進行疊加即可，即六連桿裝置的垂向平動剛度為式（23）：

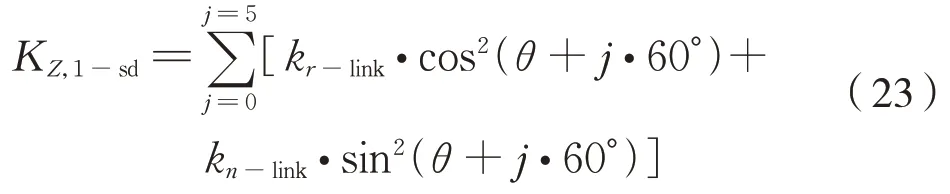
簡化得式（24）：

將式（1）和式（9）代入式（24），就得到六連桿裝置在僅考慮純垂向平動時的剛度為式（25）：

式中：KZ，1-sd為六連桿裝置僅考慮垂向平動的剛度；kr、kt、L分別為橡膠關節的徑向剛度、扭轉剛度和連桿基準長度。

可以證明，式（25）適用于所有具有“六連桿均布”特征的六連桿裝置。

（2）考慮空心軸側滾（從動齒輪與車輪保持相對平行）

空心軸側滾示意圖如圖6 所示，由于空心軸相對于從動齒輪產生側滾角位移α，6 根連桿的B 端關節相對于A 端關節有大小不一的橫向位移。空心軸側滾剛度分析如圖7 所示，假設某連桿A 端芯軸連接在從動齒輪上，B 端芯軸固結在傳動盤（與空心軸固定）上，那么B 點相對于傳動盤中心的位置可用極坐標（R，θ’）表示。則B 端芯軸相對于A端芯軸橫移量ΔSy為式（26）：

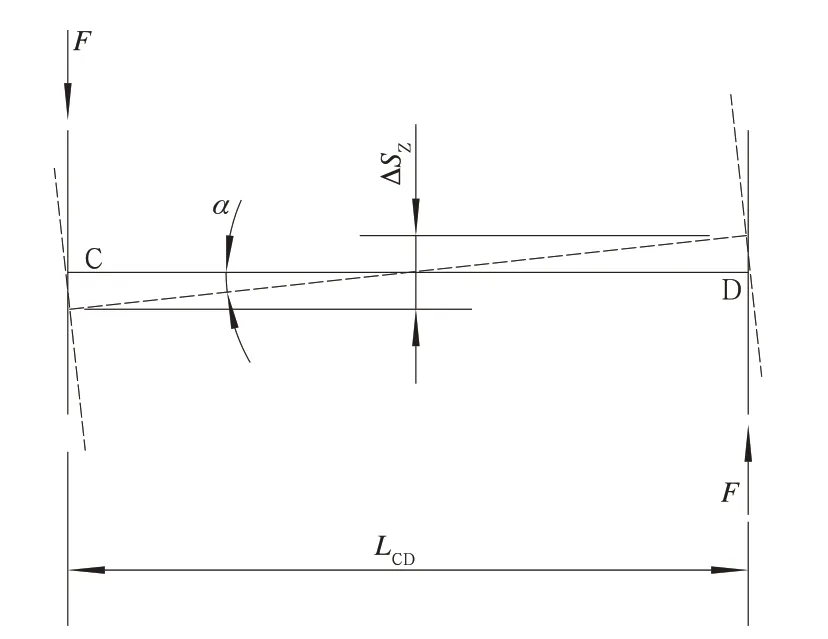
圖6 空心軸側滾示意圖

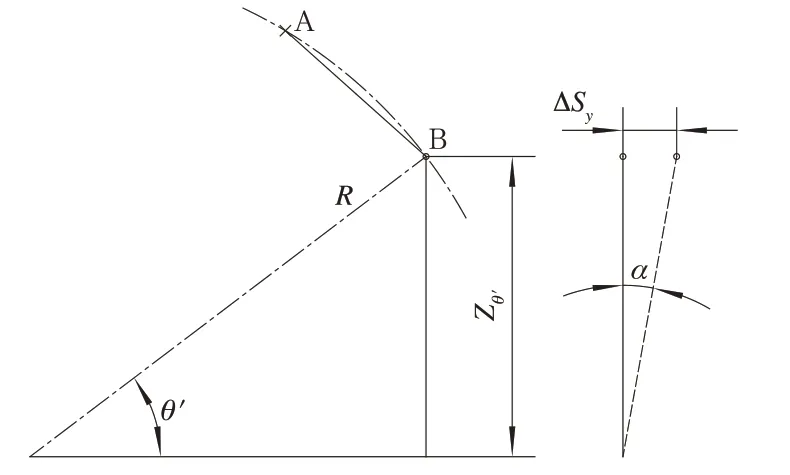
圖7 側滾剛度分析

式中：Zθ′=R?sinθ′ 。

對于橫向剛度為ky-link的連桿，兩端相對橫移ΔSy時的復原力Fy，θ′為式（27）：

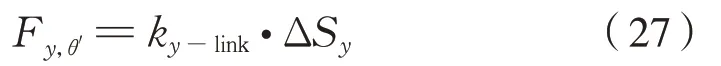
由此產生的側滾復原力矩Mθ′、進而得到該連桿的側滾剛度kθ′，roll計算公式為式（28）～式（29）：

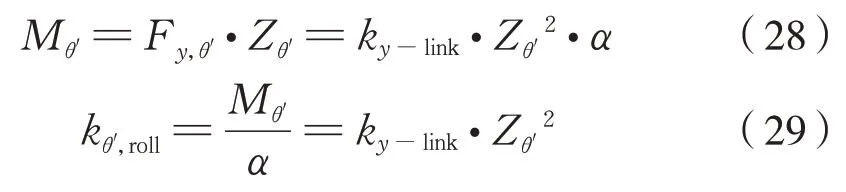
代入Zθ′得到式（30）：

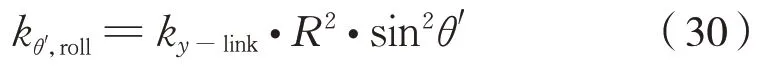
則六連桿裝置的合成側滾剛度Kroll，1-sd為式（31）：

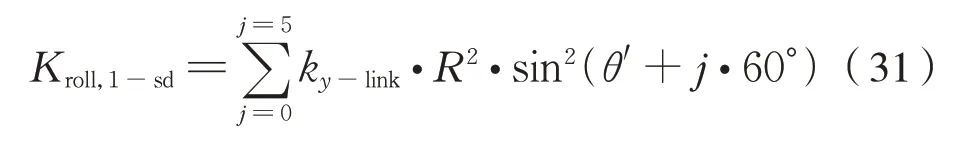
經簡化得到式（32）：

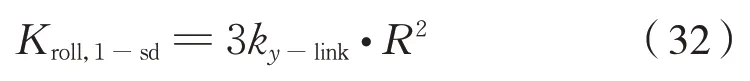
式 中：Kroll，1-sd為 單 級 六 連 桿 裝 置 側 滾 剛 度；ky-link、R分別為連桿橫向剛度和傳動銷定位圓半徑。

可以證明，式（32）適用于所有具有“六連桿均布”特征的六連桿裝置。

空心軸側滾剛度由齒輪側和車輪側2 級六連桿裝置側滾剛度并聯得到，即為式（33）：

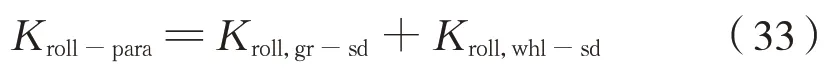
式 中：Kroll-para為 空 心 軸 側 滾 剛 度；Kroll，gr-sd、Kroll，whl-sd分別為齒輪側和車輪側六連桿裝置的側滾剛度。

由圖6 可知，對于橫向跨距LCD的2 級六連桿裝置，側滾α時兩側高度差ΔSz為式（34）：

考慮整套傳動機構力矩平衡，有式（35）：

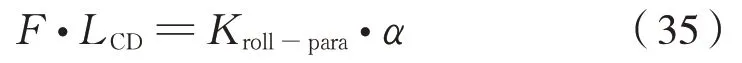
因而可得到傳動機構在考慮空心軸側滾時的垂 向 剛 度Kz，roll為：

（3）合成垂向剛度

將車輪側、齒輪側六連桿裝置垂向平動剛度和考慮空心軸側滾的傳動機構垂向剛度串聯計算，可得到傳動機構合成垂向剛度Kz，即有式（37）：

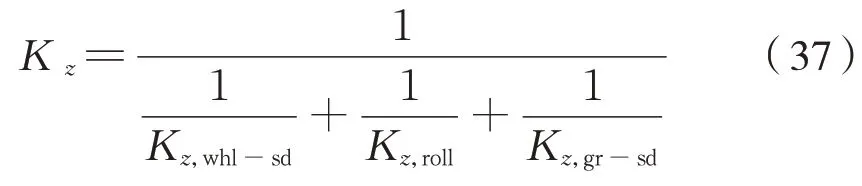
式 中：Kz，whl-sd、Kz，gr-sd分 別 為 車 輪 級 和 齒 輪 級 六 連桿裝置垂向平動剛度，值按式（25）計算。

從前述分析過程以及推導得到的相關公式可以看出，傳動機構合成垂向剛度與機車行進過程中輪對旋轉的瞬時角度無關，即徑向同性。

3.4 縱向剛度

由于2 級六連桿均布，傳動機構縱向剛度與垂向剛度相同，即為同一徑向剛度。

3.5 側滾剛度

前文對空心軸側滾運動作了分析，推導出了單級六連桿裝置側滾剛度計算公式，即式（32）。而傳動機構總的側滾剛度，考察的是從動齒輪相對于車輪發生側滾的情況，即將2 級六連桿裝置側滾剛度作串聯計算，得式（38）：

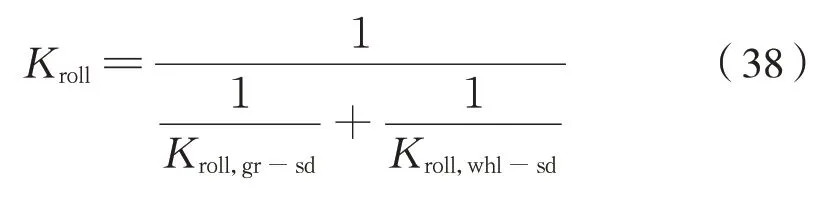
4 計算實例

以某寬軌準高速機車轉向架輪對空心軸傳動系統為例，利用前文推導出的計算公式對傳動機構各向剛度進行了計算。已知條件見表1，各剛度計算結果見表2。

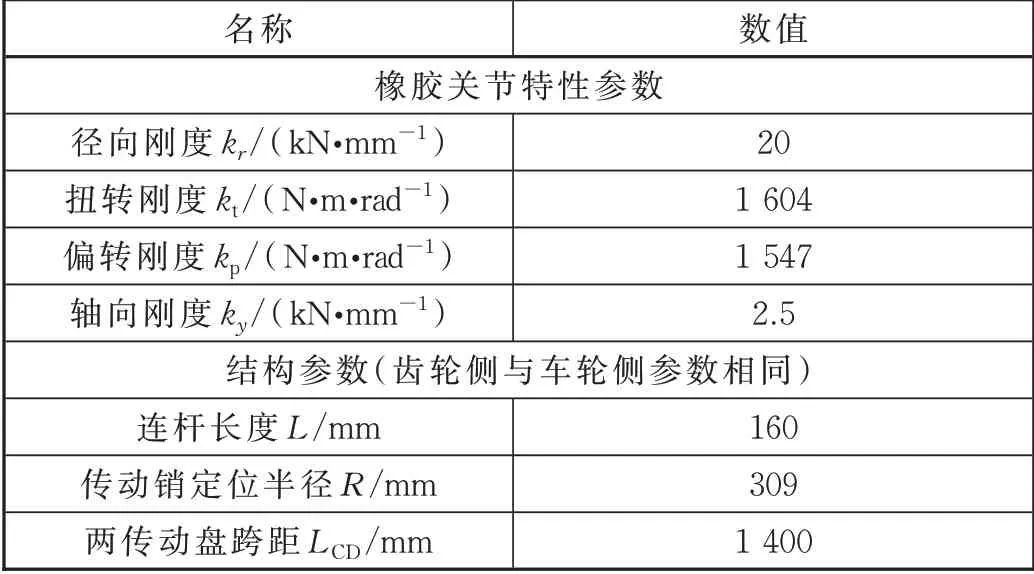
表1 實例主要參數

5 仿真驗證

為驗證推導出的傳動機構各向剛度計算公式的準確性，利用SIMPACK 動力學分析軟件對第4節給出的傳動系統建立了詳細仿真模型；并基于常見工況對各向剛度進行了動力學仿真分析。仿真結果及與利用剛度公式計算結果的對比情況見表2。可以看出，2 種方法得到的結果最大偏差僅7.8%，吻合良好，表明剛度計算公式是準確的。

表2 2 種方法得到的傳動機構各向剛度結果比較

關于仿真分析，需要補充說明的是：（1）仿真得到的橫向剛度隨相對橫向位移量的增大而增大，但增大幅度不超過2%；表中列出的仿真剛度值是偏離靜態平衡位置較小位移下的仿真值。（2）從文中實例來看，雖然徑向剛度和側滾剛度仿真結果與剛度公式計算結果相差約8%，但兩者的數值均很小，對動力學性能的影響可以忽略。

6 結 論

利用經典力學方法推導出了輪對空心軸六連桿傳動機構各向剛度的計算公式。運用這些公式，可大大簡化傳動系統的力學模型，提高驅動裝置方案對比研究和優化的工作效率。

為驗證剛度公式的準確性，用SIMPACK 軟件建立了傳動系統的仿真模型，經過一系列典型工況的仿真分析，證實了在常見位移范圍內空心軸傳動機構各向剛度可視作常值，表明利用經典力學方法推導出統一的剛度公式來計算所需剛度這一做法是可行的。仿真得到的剛度與利用公式計算出的剛度吻合較好，表明剛度公式的準確性滿足工程應用需要。