基于SIMPACK 的一種山地齒軌車動力學分析

陳雙喜

（成都大學 機械工程學院， 成都 610106）

1812 年，英國工程師John Blenkinsop 構想了世界上最早的蒸汽齒軌機車模型。1869～1871 年，美國華盛頓山齒軌鐵路［1］、歐洲瑞士瑞吉山齒軌鐵路［2］投入運營。截至2014 年全世界已有30 多個國家 開通180 多 條齒 軌 鐵 路［3］。2020 年3 月，國 內 首條山地齒軌“都江堰-四姑娘山”線路開工建設，采用“米軌+齒軌”技術，即在大坡度路段采用鋼輪鋼軌和齒輪齒條雙制式牽引方式，實現高海拔大坡度通行。

根 據 歐 洲Bundesamt für Verkehr（BAV）標準［4］，齒軌車驅動模式分為4 類：（1）純齒輪驅動；（2）通過離合器切換齒軌、輪軌驅動；（3）不同動力源驅動齒軌輪軌；（4）差分驅動。西南交通大學牛悅丞、李芾認為目前在建的“都江堰-四姑娘山”線包含輪軌和齒軌2 部分線路，第2 種驅動模式優先選擇［5］。中車資陽廠尚勤等人總結了國內外齒軌鐵路采用的新技術，提出了齒軌車輛關鍵技術發展趨勢［6］。中鐵勘察院蔡向輝等人提出一種適用于齒軌鐵路的無砟軌道技術［7］。目前，國外齒軌鐵路已有成熟應用研究［8-11］，而國內學者對齒軌鐵路的研究處于起步階段，特別是對齒軌列車關鍵技術的研究基本是空白狀態。因此，齒輪鐵路特別是齒軌列車關鍵技術的研究在現階段具有現實的應用意義。

本研究針對“米軌+齒軌”山地齒軌車，建立車輛動力學仿真分析模型，研究齒軌關鍵參數（模數、齒數、變位系數）和不同驅動模式對車輛動力學性能的影響，為齒軌列車的設計提供參考。

1 齒軌車驅動系統結構

齒軌鐵路是在傳統軌道中間鋪設一條與鋼軌平行的齒條傳動裝置的一種登山鐵路。齒軌車轉向架安裝了與齒條相匹配的嚙合齒輪。當齒軌車在大坡度地段行駛時，齒輪與齒條嚙合作用提供給轉向架走行部強大的爬坡牽引力。

齒軌鐵路軌道模式主要有Marsh 系統、Riggenbach 系統、Abt 系統、Strub 系統、Locher 系 統，其名稱均以發明人姓名（分別為Sylvester Marsh、

Niklaus Riggenbach、Carl Roman Abt、Emil Strub、Edard Locher）命名。其中前4 種系統軌道為豎向布置，Locher 系統為橫向布置。Locher 軌道系統爬坡能力最強，但機構復雜，水平齒盤與軌枕之間空間狹小，對線路養護要求較高。Abt 軌道系統有2條或者3 條齒條交錯布置，爬坡能力最低，結構復雜且齒盤較寬，但縱向穩定性高。Strub 系統使用一根齒條軌道，結構簡單，維修便宜，性價比高，可作為山區旅游線路軌道主要形式。本研究軌道采用Strub 系統。

本研究考慮了典型的適合我國旅游線路軌道的齒軌車驅動模式，如圖1 所示。牽引電機扭矩通過變速器減速后輸出給安裝在輪軸上的離合器，離合器可切換齒輪驅動和輪軌驅動模式。

圖1 齒軌車驅動系統示意圖

驅動齒輪齒條傳動幾何尺寸如圖2 所示。驅動齒輪模數m，齒數z，變位系數x，頂隙系數c*，分度圓d1=mz1，齒輪齒頂圓直徑da1，齒輪齒根圓直徑df1，齒條齒頂圓直徑ha2，齒條齒根圓直徑hf2，齒輪中心對齒條基準線距離H，齒距P=πm。

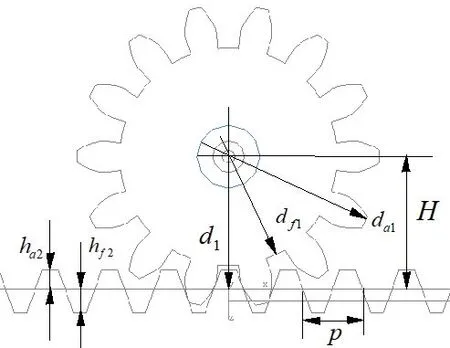
圖2 齒輪齒條傳動幾何尺寸

對于直齒輪齒條傳動，驅動齒輪軸向力為0，切向力Ft、徑向力Fr計算公式分別為式（1）、式（2）：

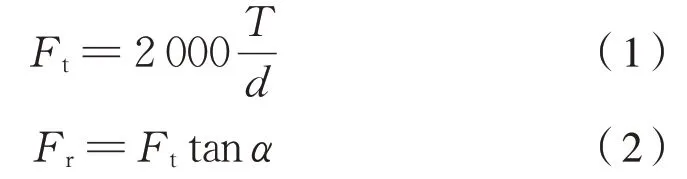
2 齒軌車動力學模型

建立單節齒軌車動力學模型，做如下假定：

（1）輪對、構架、車體、齒輪的彈性變形比懸掛系統小得多，均假定為剛體。

（2）不考慮鋼軌、齒條裝置的彈性變形。

因此，將車輛系統離散為多自由的機械振動系統，建立空間耦合動力學模型。齒軌車模型由1個車體、2 個齒軌轉向架、4 個輪對、2 個驅動齒輪盤和8 個軸箱共計17 個剛體組成。車體、轉向架、輪對為6 個自由度，即伸縮、橫移、浮沉、側滾、點頭和搖頭；軸箱1 個自由度，即旋轉運動。驅動齒輪自由度與離合器狀態有關：輪軌驅動路段，齒輪自由度為相對于輪對旋轉運動；齒軌驅動路段，齒輪相對于輪對的自由度為0。

齒軌車一系懸掛采用動車組的轉臂定位型式，二系懸掛采用空氣彈簧裝置。一系懸掛安裝垂向油壓減振器，二系安裝橫向減振器。動力學仿真模型考慮各種非線性的關系，包括：非線性輪軌接觸關系；非線性輪軌力；非線性懸掛力。

設定鋼軌類型為50 kg/m 鋼軌，軌距為1 m；車輪踏面為LMA磨耗型踏面。假定車體質量20 t，轉向架質量2 000 kg，輪對質量1 100 kg，齒輪盤質量500 kg。假定車輛定距15 m，軸距2.3 m，車輪直徑0.84 m。建立的齒軌車模型如圖3 所示。

圖3 一種齒軌車車輛動力學模型

假定后轉向架兩軸安裝驅動齒輪，黏著路段輪軌驅動；大坡度區段則考慮齒輪獨立驅動、黏著齒輪聯合驅動2 種模式。牽引力矩施加在齒輪軸上，軌道坡度最大設定為250‰。

3 仿真結果分析

3.1 典型時域分析結果

黏著齒輪聯合驅動模式如圖4 所示，動力轉向架驅動齒輪在給定扭矩下，齒軌車在250‰大坡度啟動加速到30 km/h 過程中，齒輪縱向（圖3 中x方向）牽引力Ft變化曲線。由于坡度極大，齒輪需克服較大的車輛自身重力在坡度方向分量，且在加速爬坡階段，齒輪受力極大，主要在0～140 kN 范圍內波動。齒輪受力局部放大如圖5 所示，可以看出齒輪受力在某些極短時間內為0，說明齒輪齒條存在瞬時脫離接觸情況。與驅動齒輪共軸的車輪縱向蠕滑力Tx（及縱向牽引力）變化曲線如圖6 所示，圖中車輪蠕滑力最大值數量級僅為齒輪縱向力的十分之一。因此，對于大坡度運行工況，齒輪力提供了絕大部分牽引力，且隨著坡度增大，所占比例增大。與驅動齒輪共軸的車輪的黏著飽和度[(|T|/N)/μ]變化曲線如圖7 所示，加速階段，黏著飽和度整體數值較大，車輪打滑傾向明顯，還出現一次黏著飽和度為1 的打滑現象；速度穩定階段，雖然整體上黏著飽和度整體數值降低，但出現打滑現象頻次增多。

圖4 驅動齒輪縱向力

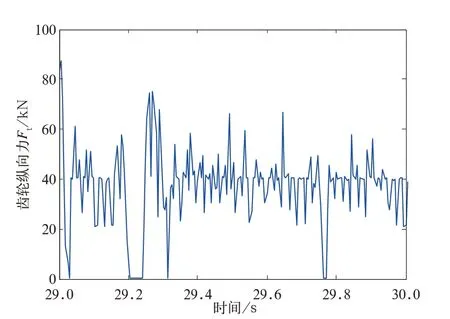
圖5 驅動齒輪縱向力局部放大

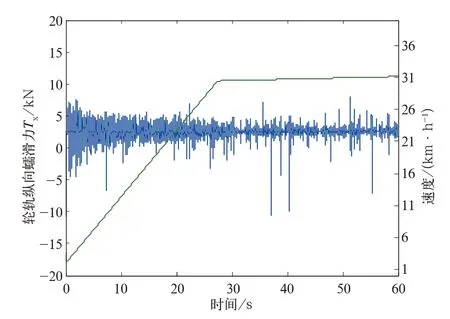
圖6 動力轉向架車輪縱向蠕滑力

圖7 動力轉向架車輪黏著飽和度

3.2 齒輪參數的影響

為了分析齒輪參數對車輛牽引性能的影響，選取了4 種方案：（1）m=20、z=42；（2）m=40、z=21；（3）m=60、z=14；（4）m=120、z=7。4 種方案齒輪分度圓直徑均為840 mm，與車輪滾動圓直徑一致。假定采用黏著齒輪聯合驅動模式，動力轉向架驅動齒輪在給定扭矩下前進，齒軌車在250‰大坡度啟動加速到30 km/h，并穩定運行30 s。

計算對比分析結果見表1，分別給出了4 種方案下，齒軌車最大速度v、平均啟動加速度A、最大齒輪縱向力Ft、最大輪軌縱向蠕滑力Tx以及最大黏著飽和度[(|T|/N)/μ]的數據。4 種方案均能實現加速到給定速度等級，時間速度曲線差別不大；4 種方案的車輛啟動加速度在0.52～0.54 m/s2范圍內，差別不大；4 種方案車輛最大黏著飽和度[(|T|/N)/μ]均為1，說明均發生了打滑現象。齒輪最大縱向沖擊力和車輪的縱向蠕滑力均隨齒輪模數增大而減小，隨齒數減小而減小。因此，選取較小模數m、較大齒數z可提高車輪黏著牽引力，但會增大齒輪沖擊力。

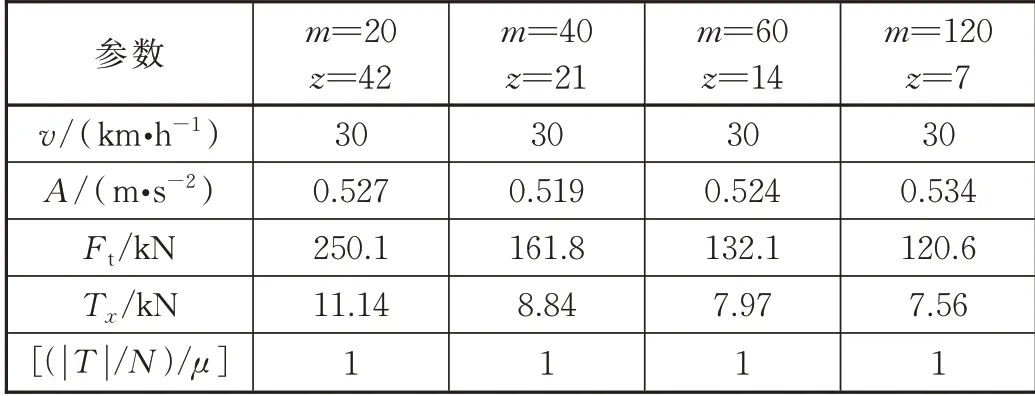
表1 不同齒輪參數的計算結果

對于軌道車輛，輪對磨耗及旋修后車輪直徑變小。而對于齒軌車車輪，輪對磨耗及旋修后齒輪中心到齒條基準線距離H變小，根據公式H=d1/2+xm，齒輪應采用負變位。為考慮齒輪變位系數的影響，假設驅動齒輪變位系數x的范圍為-0.6～0，則H的變化范圍為0～36 mm，這與車輛全壽命周期車輪半徑最大變化量（限界標準規定的輪對最大旋修量35 mm）基本一致。

不同變位系數對齒軌車速度、最大加速度的影響如圖8、圖9 所示。在相同模數、齒數（假定m=60、z=14）情況下，牽引速度隨著變位系數絕對值增大而減小。可以看出，在相同牽引扭矩下，采用不變位的標準齒輪齒條參數可牽引至給定速度30 km/h；變位系數x=-0.6 時，最高牽引為速度23 km/h，明顯低于設定值。在相同模數、齒數（假定m=60、z=14）情況下，最大啟動加速度隨著變位系數減小而增大，無變位情況下最大加速度如圖9 所示。因此，驅動齒輪若采用變位齒輪，牽引至設定速度需適當提高電機牽引扭矩。

圖8 不同變位系數的齒軌車的速度

圖9 齒輪變位系數—加速度曲線

不同變位系數對齒軌車齒輪縱向沖擊力、車輪縱向蠕滑力的影響如圖10 所示。在相同模數、齒數（假定m=60、z=14）情況下，最大沖擊力隨著變位系數減小而增大，無變位情況下最小。因此，為降低齒輪沖擊力，應選擇較小的變位系數。

圖10 齒輪變位系數—齒輪/輪軌縱向力曲線

3.3 黏著/齒軌驅動方式比較

齒軌列車需要兼容普通米軌鐵路和大坡度登山齒軌鐵路，因此在普通米軌路段只采用鋼輪黏著驅動，而在大坡度路段通過離合器切換至鋼輪鋼軌和齒輪齒條雙制式牽引方式，實現高海拔大坡度通行。本研究對純齒輪驅動、雙制式驅動進行了對比計算。

2 種驅動模式下，車輛在平直線路和250‰大坡度路段的啟動加速度時域響應分別如圖11、圖12 所示。可以看出，純齒輪驅動和雙制式驅動均能以足夠加速度牽引，但采用雙制式驅動可顯著降低縱向沖擊加速度。因此，宜采用雙制式驅動模式。

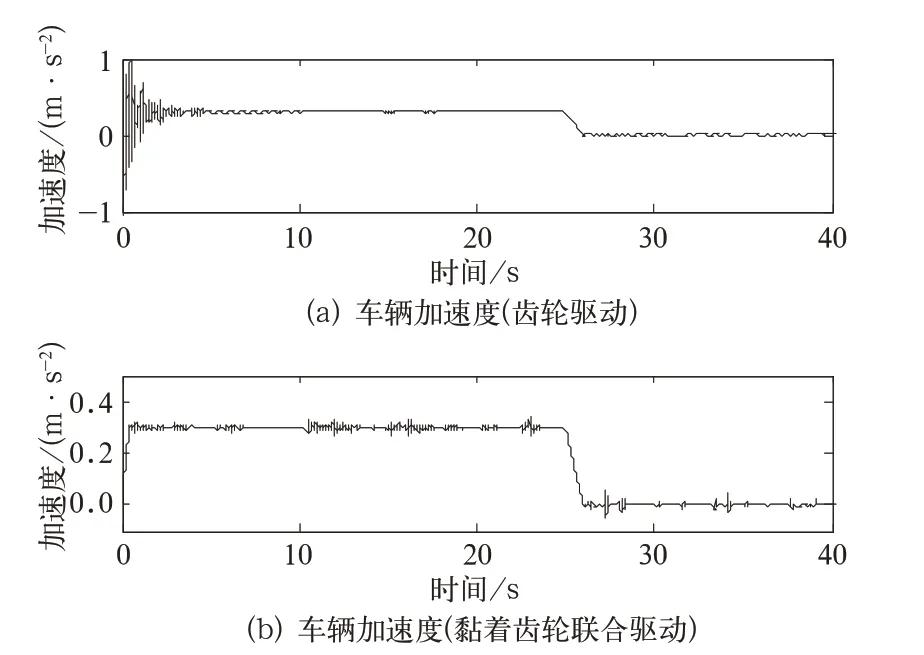
圖11 不同驅動方式下平直線路車輛加速度

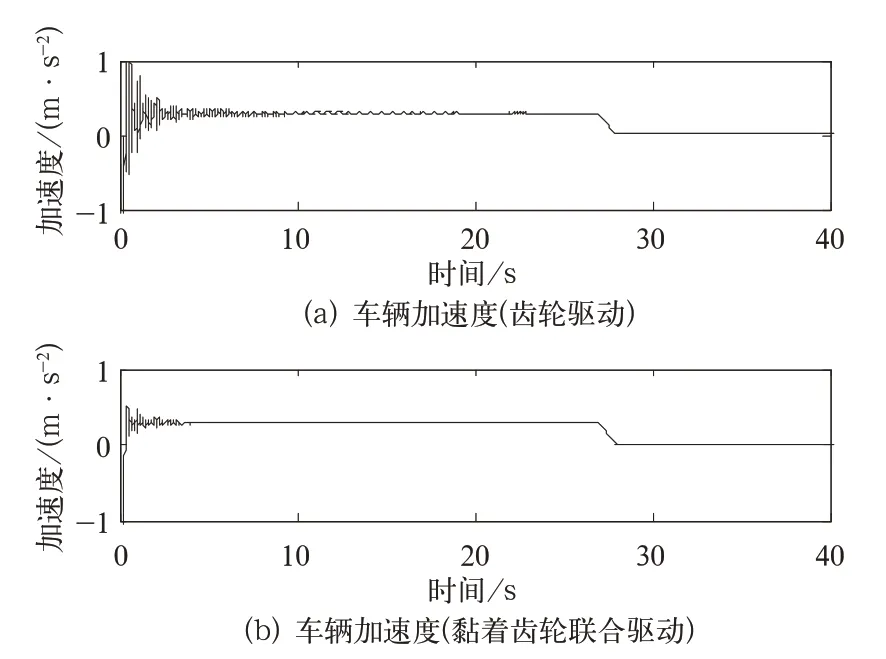
圖12 不同驅動方式下250‰坡道車輛加速度

2 種驅動模式下，在250‰大坡度路段運行，驅動軸車輪黏著飽和度[(|T|/N)/μ]曲線如圖13 所示。可以看出，雙制式驅動模式下車輪黏著飽和度明顯大于純齒輪驅動，但也存在打滑現象。

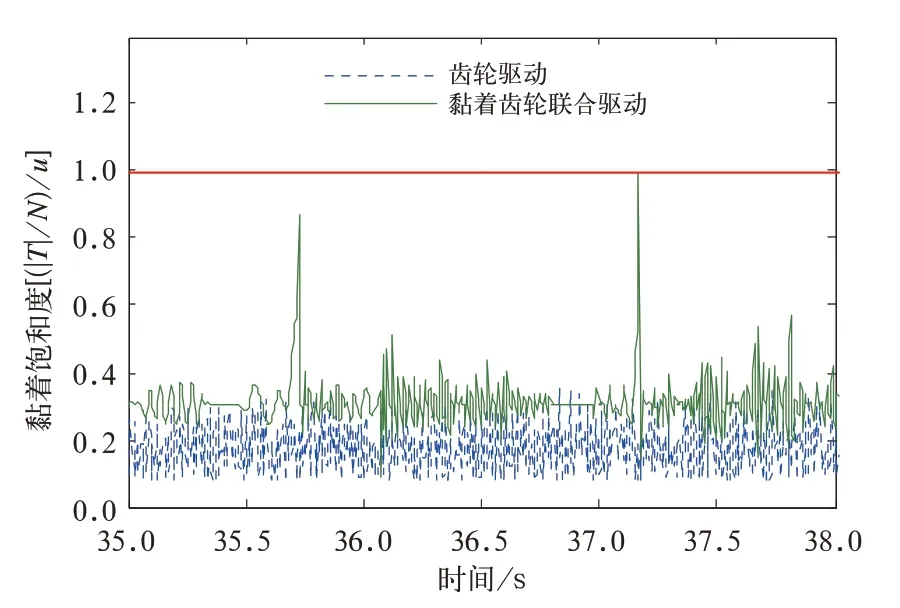
圖13 不同驅動方式下250‰坡道車輪黏著飽和度

此外，本研究也對250‰大坡度路段啟動全過程，2 種模式下車輛的脫軌系數進行了計算。結果表明雙制式驅動模式下車輪脫軌系數0.03，而純齒輪驅動模式下車輪脫軌系數0.19，均滿足GB 5599—2019《機車車輛動力學性能評定及試驗鑒定規范》、GB 17426—1998《鐵道特種車輛和軌行機械動力學性能評定及試驗方法》以及DB51/T 2542—2018《山地（齒軌）軌道交通技術規范安全標準》。對比也表明雙制式驅動模式下具有更高的運行安全性。

4 結 論

目前國內的齒軌列車還處于研究設計階段，沒有成熟的車型，本研究為我國齒軌列車的設計提供技術參考。通過對一種山地齒軌車的建模、計算與對比分析，得到如下結論：

（1）驅動齒輪模數齒數對牽引加速度影響不大，相同分度圓半徑下選取較小（較大）模數可提高（降低）車輪黏著牽引力，增大（減小）齒輪沖擊力。

（2）驅動齒輪變位系數對牽引性能影響較大，宜選擇較小的變位系數。

（3）鋼輪鋼軌和齒輪齒條雙制式牽引方式優于純齒輪牽引，具有更好的安全性。