基于公平性的大型機場停機位指派優化研究

劉銀輝 袁 琪 姜 雨

(南京航空航天大學民航學院 南京 211106)

0 引 言

停機位指派是指在在停機位服務時間內，由運控中心將n個航班合理的指派至m個停機位，保證航班運行正常一個過程，由于大型機場航班數量大，停機位數量多，屬于NP-hard問題.近年來，停機位指派優化問題成為行業研究熱點.Nikulin等[1]以航空器的被牽引數量最小，停機位指派與計劃偏差最小為目標構建停機位指派模型.馮程等[2]以旅客出入飛行區的時間最少為目標建立停機位指派模型，并選擇滑行路徑優化作為提高停機位指派效率的關鍵因素.Prem等[3]從成本、運營收入、機場魯棒性等方面建立多目標指派模型.Deng等[4]以最短化旅客的步行距離、最小化停機位空閑時間和合理利用大型停機位作為優化目標構建模型，并設計改進了自適應粒子群算法進行求解.Sena[5]以最短化旅客步行距離為目標，并考慮指派到離機場購物區最近的旅客數量，以促進機場銷售運營.姜雨等[6]設計了以滑行道路徑規劃在上、以停機位再分配在下的雙層規劃模型，為場面運行中停機位再指派多目標模型的建立提供了新思路.對于由多個相互制約影響的單目標組成的多目標模型，現有求解方法包括優先級法[7]、線性加權法[8]等.也有研究采用約束法將其轉化為單目標模型并用啟發式算法[9-10]求解.

目前對停機位指派的研究大多集中于對停機位運行效率、航空公司運行成本或是旅客滿意度等單個或兩個主體進行，其優化結果難以滿足多方利益.由此可見，綜合考慮機場、航空公司和顧客三個利益主體進行的停機位指派優化研究有其必要性和先進性.因此本文兼顧多方利益，同時融入航空公司間公平性原則，構建停機位指派多目標優化模型，并尋找有效求解方法，為大型機場停機位調度提供決策依據.

1 模型建立

1.1 模型假設

1) 在停機位指派之前，航班的基本信息和停機位狀態均齊備已知.

2) 停機位指派在實際運行時是連續的、動態的，假設只指派一個時間段內的航班.

3) 機場的所有停機位足夠為時間段內每個航班提供停靠服務.

4) 航班從指定的停機位到跑道端、從安檢點到登機口、從停機位至行李提取點的距離均為固定且已知的數.

5) 本文的航班指一個航班對.

1.2 模型建立

1.2.1目標函數

文中以停機位的占用時間均衡為基本目標，旨在提高機場停機位的利用效率，使停機位的保障人員有一個合適的平均勞動強度。此外，旅客步行時間是影響機場服務水平評價和航空公司印象的重要標準之一，飛機的滑行油耗成本是航空公司總運行成本的重要部分.但為使旅客步行距離最小，擁有旅客數量少的航空公司的航班往往被指派到遠機位，同理為降低總油耗將會使擁有航空器機型小的航空公司的航班被指派到里跑道端較遠的停機位.綜上，本文考慮機場、旅客與航空公司利益設置下列目標函數.

(1)

(2)

(3)

(4)

(5)

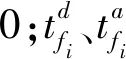
式(1)為最小化各停機位占用時間平方和，Z1值越小，代表機場停機位利用率越高；式(2)為最小化平均每旅客步行時間，一般來說，Z2值越小，旅客滿意度越高；式(3)為最小化總滑行油耗成本，Z3值越小，航空公司的利潤更能得到保障；式(4)為各航空公司之間在每旅客平均步行時間上的均衡，式(5) 為各航空公司之間在滑行的成本上的均衡程度。Z1、Z2、Z3值若均在較小的合理范圍內，這說明機場、航空公司和旅客三方的利益得到了均衡與保障，Z4、Z5值越小，則代表航空公司之間的指派越公平.

1.2.2約束條件

(6)

(7)

(8)

(9)

(10)

(11)

式中：T為同一停機位上連續兩航班之間最短間隔時間；δ為被指派到相鄰兩停機位的兩航班的最小間隔；σ為被指派到遠機位的航班停機時間限制；U為足夠大的一個值；Pfi為航班fi使用的航空器型號；Pgk為停機位gk的類型；Zfi,fj為輔助變量，航班fi為航班fj的前序航班，當航班fi和航班fj指派到同一個停機位，Zfi,fj的值等于1，反之為0；K為遠機位編號.

式(6)為每個航班都需要被指派一個停機位，且只能被指派到一個停機位；式(7)為每個停機位在同一個時段里面只能供一個航空器停靠；式(8)為派到相同停機位的連續兩個航班之間必須有相應的間隔時間；式(9)為停機位之間最小安全鄰近間隔約束，即指派到相鄰停機位的兩個航班，要注意推入與推出的最小時間間隔，以避免相鄰航空器發生碰撞；式(10)為停機位與機型大小約束；式(11)為盡量使停機時間小于σ的航班不指派到遠機位所做的約束條件，以免為了實現第一個目標函數而將一定數量航班分配到遠機位.

2 算法設計

使用遺傳算法求解時將對各個目標設置優先級，五個目標將分別被設置為第一優先級進行五次試驗.采用十進制整數編碼的方式，染色體上的基因代表停機位編號，染色體長度為航班總數，根據停機位編號隨機生成初始種群，并根據目標函數與優先級計算個體適應度。經過交叉、變異操作后，選擇目標函數值最小的N個個體進入新種群，其中交叉過程為奇數染色體與偶數染色體進行多點交叉，變異操作選擇隨機變異法[11].

NSGA-II算法不設置目標優先級，而是同時對5個目標進行求解.NSGA-II算法在遺傳算法的基礎上，增加非支配排序和聚集距離排序的過程[12].步驟為

步驟1將父代與經過交叉、變異后的子代合并，得到2N個個體.

步驟2對2N個個體計算多個目標函數值，采用規模為2的錦標賽方式，即兩兩個體進行比較，判斷每個個體之間是否存在支配關系，支配關系指的是一個個體A的各個目標函數指標均比另一個個體B優越，則稱A支配B，否則為非支配關系.

步驟3根據個體之間的關系分為若干層，每層里面的個體為非支配關系，上層對下層的個體為支配關系.

步驟4對每層的非支配的個體計算它們的聚集距離，個體的聚集距離等于與其最鄰近的兩個個體在每個單目標上的目標函數值上的差距相加，聚集距離大的個體適應度越高.

步驟5由上層開始選取N個個體組成新的子代種群.

圖1為NSGA-II的新種群構成示例。

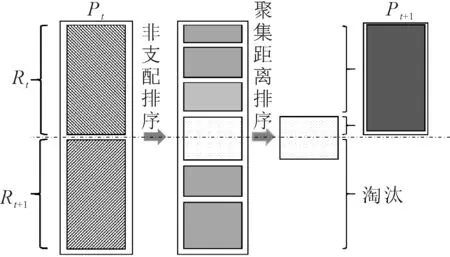
圖1 NSGA-II的新種群構成示例

3 仿真驗證

數據來源于長沙黃花國際機場2020年4月8日的航班運行數據，選取當天08:30—18:00時間段內由五個規模不等的航空公司服務的76個國內進離港航班進行仿真驗證，航班數據示例見表1，其中一條航班數據為兩個航班組成的一個航班對.選擇機場T2航站樓停機位號為211-216、221-228的14個近機位及241、242的2個遠機位共16個機位為研究對象，編號為1-16，所在位置見圖2，停機位的基本狀態信息見表2，其中遠機位的旅客步行距離在實際步行距離上加上了一段“懲罰距離”，以更符合實際運行過程中的旅客心理.另外在模型中涉及到的其他參數設置見表3.

表1 研究時段內進離港航班數據示例

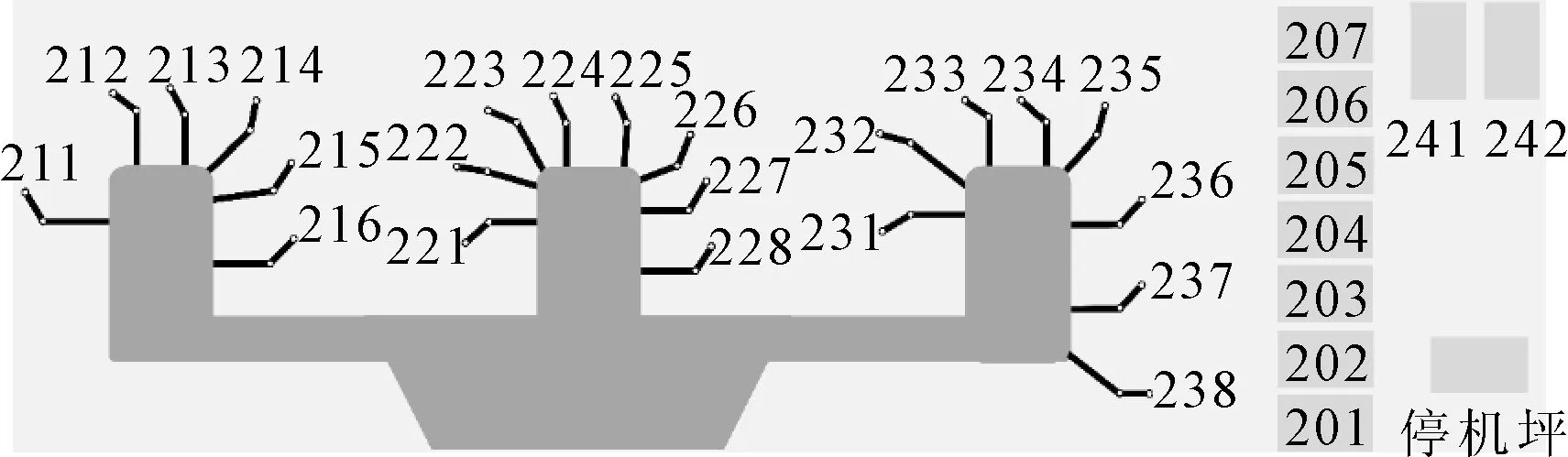
圖2 長沙黃花國際機場T2航站樓停機位編號示意圖

3.1 基于遺傳算法的停機位指派結果分析

使用Matlab R2018a版本，按照遺傳算法的思想，采用優先級的方法為多目標模型進行編程和運算.根據多次實驗結果發現，當種群為100，最大進化次數為500次是速度最快、效果最好，因而將種群大小設置100，最大進化次數為500，交叉概率設置為0.8，變異概率為0.08，產生的不同目標優先級最高條件下的優化結果見表4.

表3 實例參數設置

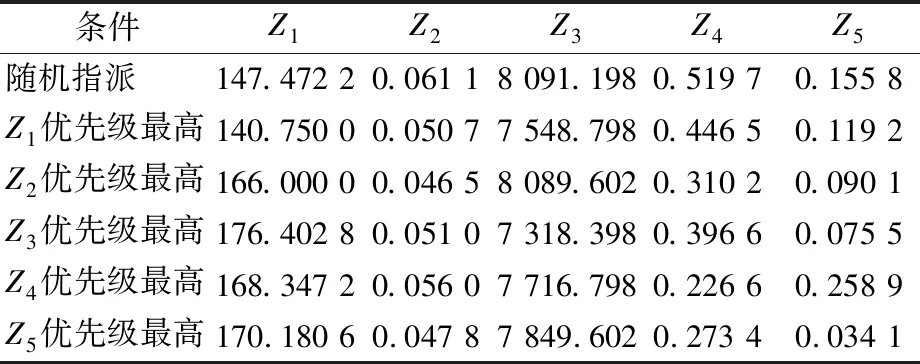
表4 基于遺傳算法求解的五種條件下的結果比較

由表4可知：當以停機位占用時間均衡為優先級最高的目標條件下，此時停機位的利用率較高，但Z4和Z5的目標函數值均偏大，說明此時以機場效率作為單個目標考慮會削弱公平性.

將旅客步行時間最少設置為目標優先級最高的條件下，也出現Z4和Z5的函數值普遍偏大的情況，并且當設置滑行油耗最少為優先級最高的目標時，停機位的占用時間指標非常大，比最低Z1值高出了25%，說明算法為了降低油耗將航空器分配到了離跑道端較近的停機位上，導致了離跑道端較遠的停機位得不到有效利用.

當目標為航空公司的旅客步行時間最均衡和航空公司的航班滑行時間最均衡時，代表停機位占用時間的目標值過大，說明只考慮絕對公平也會導致機位資源上的浪費.

3.2 基于NSGA-II算法的停機位指派結果分析

使用Matlab編寫NSGA-II算法程序，對五個目標同時進行求解仿真.經過多次試驗，將種群大小設置為100，進化次數為800，同樣以0.8的概率進行交叉，以0.08的概率變異. 使用NSGA-II算法對模型的五個目標同時進行求解后得到的多個pareto解中，人工分別側重Z1，Z2，Z3，Z4，Z5值最優條件選出5個解，見表5.

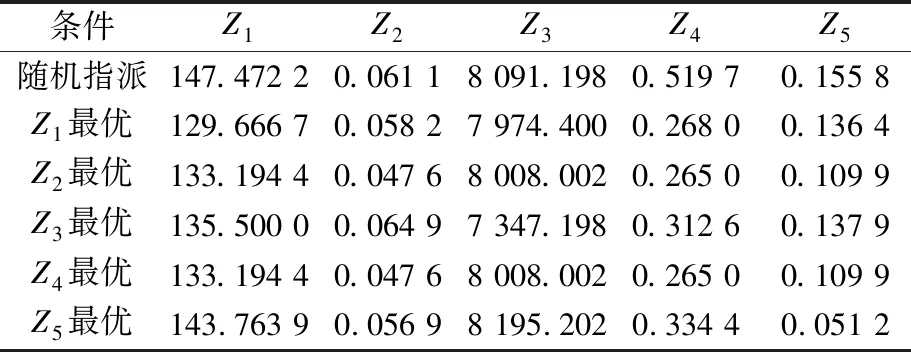
表5 基于NSGA-II算法求解的pareto前沿解

由表5可知：各個指派方案互不支配.相比隨機指派方案，使用NSGA-II算法求解得到的不同條件下的方案，其各個目標值均在一個合適的范圍內，其中Z1各值均在150以下，Z4值均保持在0.35以下，Z5值均保持在0.20以內，其中有4組方案的Z5值在0.15以下，Z2，Z3在個別條件下比隨機指派方案的目標函數值高，但增加幅度不到6%.

在產生的pareto解中選擇一種方案與隨機指派方案進行對比，見圖3，任務框中的數字代表航班所屬航空公司.

由圖3可知：隨機指派條件下的停機位指派將4個航班分配到了遠機位，G10沒有得到利用，G7、G3等停機位則十分繁忙，需要服務4～5個航班，而NSGA-II求解模型得到的停機位指派方案各個近機位得到了均衡利用，均有2～4個航班，且只有1個航班被分配到遠機位.停機位號為211-216即編號為1-6的近機位步行時間較遠，而基于NSGA-II算法得出的方案中，對于標號為5的航空公司的小型航班在使得旅客步行時間盡可能小的情況下，沒有被分配到遠機位，而是大部分被分配到了步行距離稍遠的近機位，說明算法保障了第二個目標與第四個目標的同時實現.

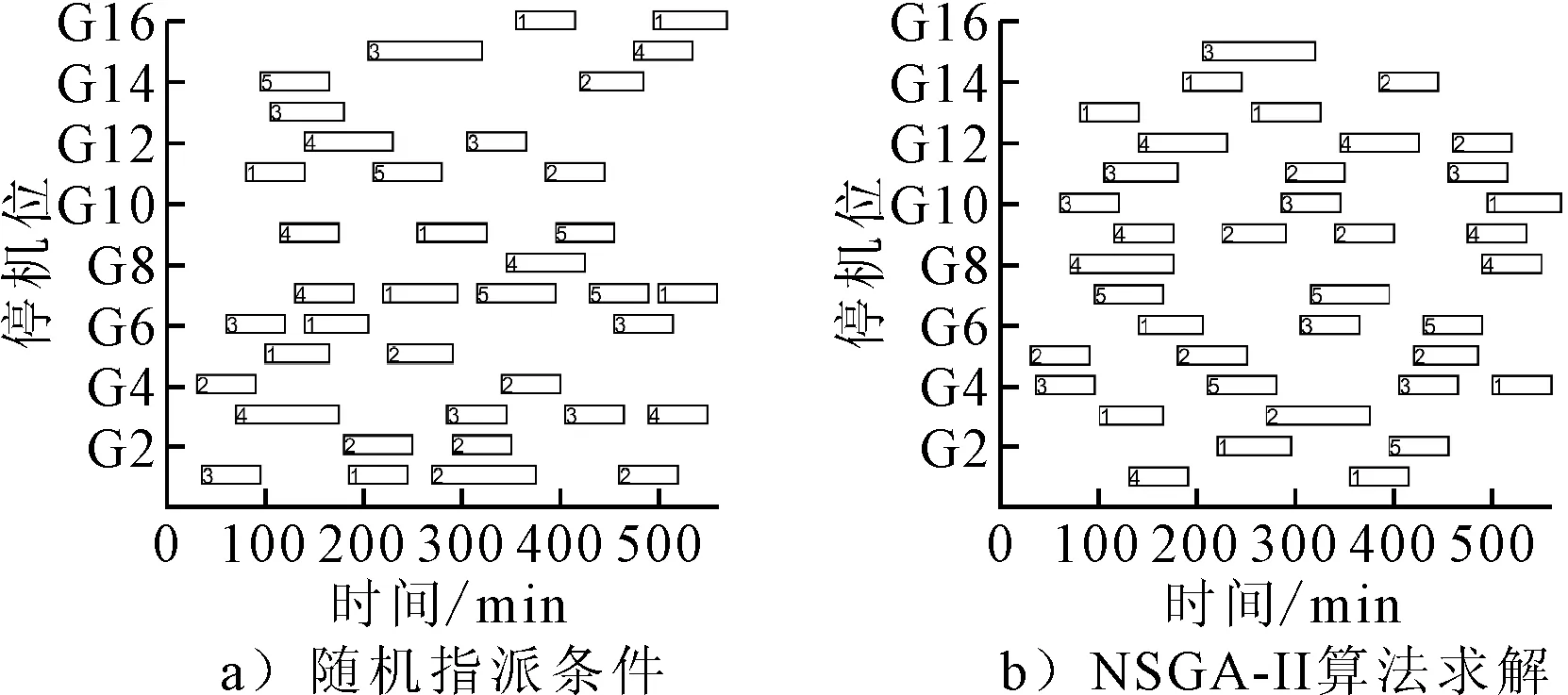
圖3 停機位指派甘特圖

將NSGA-II算法在各個條件下的目標函數值與遺傳算法相比，發現基于NSGA-II算法求的Z1值均優于遺傳算法，其值相比遺傳算法平均降低17%；Z4值在大多數條件下優于遺傳算法，且變化幅度穩定；Z5值雖在大部分情況下高于遺傳算法所得到的目標值，但其變化幅度仍比遺傳算法要穩定，見圖4.由圖4可知：相比遺傳算法，基于NSGA-II算法求解的Z2值在大部分條件下有所升高，但其最大變化幅度在30%以內，平均每旅客步行時間仍控制在4 min以下.基于NSGA-II算法求解的Z3值與其變化幅度相比遺傳算法均有增加，但其變化幅度的增加仍控制在10%以內，表明算法在用場面滑行總油耗的合理增加換取停機位占用時間均衡，以保障停機位資源利用效率.

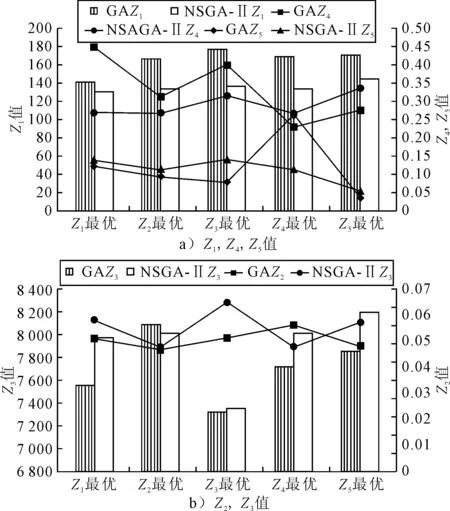
圖4 不同條件下遺傳算法與NSGA-II算法

綜上所述，在選取合適的算法運用于該模型時，不僅可以兼顧機場停機位利用率、旅客步行距離和航空器滑行油耗等因素，還能使得航空公司之間在滑行距離與旅客滿意度上也保持相對的公平，滿足了旅客和航空公司的服務要求，促進了停機位的有效利用.

4 結 論

1) 從大型機場停機位指派過程中涉及的機場、航空公司與旅客的利益出發，構建了基于公平性的停機位指派多目標優化模型.

2) 使用NSGA-II算法對模型進行求解，結果發現各個條件下的解的目標函數值均在合理的范圍之內，其中Z1各值均在150以下，Z4值均保持在0.35以下，Z5值均保持在0.20以內，緩解了機位指派過程中提高了效率卻要犧牲公平性的問題，為停機位指派中協調各方利益提供了一種可行思路.

3) NSGA-II算法求解得到的方案比隨機指派方案求解得出的Z1目標函數值均優，使停機位利用效率提高8%.相比遺傳算法，NSGA-II算法求解得到的Z1各值平均降低17%，其他各值的變化幅度均在合理范圍內，驗證了模型與求解的有效性.

4) 使用航班數據均為固定已知，下一步研究可考慮如何在大面積延誤、航班取消等應急情況下兼顧公平性進行停機位指派，使研究更符合實際運行情況.