大型風力機變槳角度對尾流特性影響的研究

孫芳錦， 賀偉盼， 鄧富河， 盧 琛， 張大明

(1. 桂林理工大學土木與建筑工程學院，廣西 桂林 541006; 2. 廣西嵌入式技術與智能系統重點實驗室，廣西 桂林 541006;3. 桂林理工大學信息科學與工程學院，廣西 桂林 541006)

0 引 言

在當今世界，石油、煤炭、天然氣等不可再生能源，隨著人口的增長，生產力的發展，消耗越來越多越來越快，碳中和的呼聲越來越受關注。現今世界，最讓人關心的問題就是能源問題，它已經成為了當今世界政治、經濟、科技、軍事等人類領域的重點問題。傳統能源很可能會出現能源危機，即能源的供應不足、儲量銳減，如果沒有可代替的其他能源，那么只能有意地控制能源的開采和使用，進而加劇市場供應的不足，能源價格上漲，影響到社會運行。風力發電作為清潔能源，具有顯著的環保意義，社會發展價值和巨大的經濟效益，因此風電的發明有著劃時代的意義。地球上的風能蘊量巨大，約為2.74×109MW，其中可利用的風能大概為2×107MW，僅僅只占總量的百分之一左右，全球可以利用的水能能源總量約為可用風能的十分之一，也大于固體燃料和液體燃料能量的總和[1]。總量雖大，但是真正被利用開發得不多，想要安全、可靠、有計劃地使用好這些沒有被利用的風能就需要更好地研究風力機的各種受力特性以及尾流等。任年鑫等[2]采用RAN k -ω湍流模型，三維數值模型的有效性得到了很好地驗證。但是缺少對風力機變槳角度改變的研究。張亞光[3]使用AL-LES方法預測風力機尾流非定常流動特性的可行性，但是大渦模擬不是很適用于風力機的計算。劉海鋒等[4]運用Fluent軟件，在11.4 m/s風速下，風輪轉速為12.1 r/min，變槳角為0°時，使用流固耦合理論和滑移網格技術得出尾流特性的系統分析。是在特定的情況下得到的結果，不具有一般性。楊從新等[5]采用大渦模擬與致動線模型相結合的數值方法，模擬了多臺NREL 5 MW風力機的風電場情況。但是在實際的應用中，大型風力機一般是獨立存在的。劉智益[6]等提出串聯多風力機以及錯列雙風力機的三維尾流模型，并通過修正尾流區域的膨脹系數 k來驗證模型正確性。前人一般都是研究在來流風和風力機之間沒有變槳角的情況下的尾流等氣動特性，幾乎沒有研究過單臺大型風力機變槳情況下的尾流特性，因此本文對此問題進行了探討。

在實際中，來流風一般不會恰好與風輪所在的截面成90°流入，本文首先用ANSYS-Fluent穩態模擬計算功率和實驗數據對比，對比誤差均在20%以內，說明了本文的準確性。然后采用ANSYS-Fluent的瞬態計算，得出尾流的壓力和速度云圖，最后得出結論，分析原因。

1 理 論

1.1 CFD技術

CFD的全稱是Computational Fluid Dynamics，中文稱之為計算流體力學。CFD技術是基于流體力學和數值數學的理論基礎，再運用現代的計算機技術將其計算結果可視化的產物。經過前人不斷地完善計算模型和多次實驗數據對比分析，CFD技術可作為準確的重要數據來源，因具有成本低廉，可視化程度高，以及準確度高等優點被人所喜愛。學者們先后提出一系列的工程尾流模型，但是最適合本文的計算模型還是 k -ω SST模型。目前主流的通用求解器有 CFX、Star - CD、Fluent 、star - ccm +AUTODESK CFD flow-3D、Phoenics、Comsol，其中CFX、Star - CD、Fluent等[7]，能夠解決各類流體問題。本文本著節約成本和同時兼顧準確性的原則選用了Fluent軟件對大型風力機進行數值模擬。

1.2 k -ω SST湍流模型

由Menter[8]提出剪切應力輸送(Shear-Stress Transport，簡稱SST)，該模型在近壁面自由流中具有較好的計算精度，因為其綜合了近壁面區計算的優點和在遠場計算的優點，在湍流粘性系數的定義中添加了湍流剪切應力的輸送過程，并且增加了交叉擴散項。在風力機的計算中風力機的翼型屬于低負荷的模型，僅僅在風力機的輪轂位置處屬于鈍體繞流，因此適用于本文的風力機數值模擬計算。該湍流模型的方程為：

2 實例驗證

2.1 建立模型

本文選用位于美國科羅拉多州大丹佛地區的可再生能源實驗室（NREL）5 MW大型水平軸三葉片海上風力機作為本文的計算實例，風力機風輪葉片長度為61.5 m，其輪轂直徑為3 m，風力機的直徑為126 m。該5 MW風力機使用變速變槳的功率控制方式，相對于功率較小風力機，是具有代表性和實際應用意義的大型海上風力機，很有研究的意義。5 MW風力機葉片各個截面幾何參數[9]見表1。

表1 NREL 5MW 海上大型風力機葉片幾何參數

風力機葉片的建模，首先根據表1在profili軟件中獲取到原始的翼型坐標，然后向左平移后坐標變換，根據安裝扭角在Excel中計算得出風力機葉片的實際坐標點，為了使葉片可以更好地連成一個整體，將第一個截面為一個圓形的截面形狀，最后把所有的坐標導入Solidworks中，最終建成的葉片的三維效果圖如圖1所示。

圖1 5 MW風力機三維單葉片圖

在單個葉片的基礎上畫出一個3 m直徑的輪轂之后，再使用陣列功能得到三葉片的整體風力機如圖2所示。

圖2 三維葉輪圖

2.2 確定計算域和劃分網格

為了使得風力機的尾流流域得到充分精確計算，內流域為設置為一個圓盤形狀的旋轉域，尺寸為直徑140 m，前后內流域壁面到風輪中心基準面距離為10 m的圓柱，將外流域設置為一個5D×5D×12.5D（D為風力機直徑126 m，下文中均以D表示風力機直徑）的長方體計算域，其中風力機所在基準截面到進口面的距離為，出口面距離風輪基準面，風輪中心到上下左右壁面的距離為。由于直接計算原尺寸的風力機模型，風場過大，建模困難，因此本文采用縮小為原來的模型來計算。內外流域圖如圖3所示。

圖3 內外流域圖

使用 A NSYS-ICEM劃分網格，風力機計算域整體采用混合結構網格，其中內流域采用非結構化網格，外流域為結構化網格。網格的劃分是決定計算準確的最重要的因素，為使得計算更加精準，需要在外流域和風力機邊界層加密網格。最終的網格數目為三百多萬個如圖4所示。

圖4 流域混合結構化網格劃分

2.3 功率驗證

將畫好的網格導入到ANSYS-FLUENT中運算，計算的參數根據實驗的設定輸入，選擇SST湍流模型，SIMPLE算法，穩態模擬計算。

查閱資料[9]，可以獲取在不同的來流風速下，風力機風輪的轉速、變槳角度和功率，選取了4個數據進行比對。風速為11.4 m/s的時候為額定風速，對應的額定功率為5 MW，具體的參考數據和本文模擬數據對比如下表2。由于尺寸的縮放為原來的1/10，計算所得的扭矩也隨之變為了原來的1 / 1000[10]。

表2 功率對照表

本文需要的功率計算換算公式如下：

在Fluent中只能計算出力矩的大小，因此本文采取以下的方法[11]將力矩轉化為風力機的輸出功率：

大量的，而且具有一定重復性的精準良好數值計算結果均證明FLUENT計算的正確性，數值模擬計算數值與實驗數據的誤差均在20%以內，并且越接近額定風速誤差越小，整體都是功率偏大的，可能是由于網格質量導致的。表明了數值模擬計算的可靠性和正確性。因此在接下來的案例分析中其他的參數不變的前提之下，將穩態改為瞬態。

3 大型風力機變槳角度對尾流特性影響分析

3.1 計算實例

為了使得本文的研究更具備實際性，因此研究在變槳角情況下的風力機的尾流該情況下空氣流經風力機之后會產生大面積的分離，這種情況下壓差阻力占主導地位，S-A模型是從翼型繞流的航空領域發展而來的，通過對渦粘性系數修正的方法來適應不同區域的流動，雖然計算的速度較快，但是不適合用的分離流動的具有變槳角的風力機計算中。同樣的用大渦模擬的計算結果不如RANS精準，因此選用基于SST的k-ω模型進行計算分析。

變槳角如圖5所示，定義為來流風與風力機基準面的法線夾角。

圖5 變槳角示意圖

3.2 計算參數設置

用縮比尺寸模型可以解決建模過程中計算域太大的問題，用縮比模型CFD計算的尾流與實際的尺寸實驗尾流數據相差不大[12]。

計算使用瞬態計算，重新劃分具有變槳角的風力機網格，網格數目大概四百多萬，變槳角環境下的內外流域網格劃分圖如圖6所示。計算模型選擇：SST，解決方案中的方法選用SIMPLE，梯度為Least Squares Cell Based；梯度、壓力、動量、湍流動能、比耗散率以及瞬態離散方案均選用二階計算。選擇混合初始化，在運行計算中，計算類型為Fixed，時間步長為：0.01 s，最大迭代步數為20。

圖6 21.18°變槳角時內外流網格劃分圖

3.3 大型風力機變槳角對尾流特性影響分析

3.3.1 速度壓力速度云圖整體分析

根據NREL實驗室的風力機實際工作數據，本文選取三個工況分別對應的來流風速為23 m/s,18 m/s, 13 m/s對應的變槳角度分別為21.18°，14.92°，6.60°進行尾流分析，具體如表3所示。

表3 來流風速和變槳角度對照表

如圖7～圖9所示可以得出：隨著變槳角的增大和來流風速的增加，旋轉域前后的風速分層變得明顯，且風力機的尾流影響的距離越遠；其中工況一的尾流可以到達距離風力機旋轉域中心的10D之外，三個工況共同的特點就是尾流均在4D左右就開始明顯變弱，并且在旋轉域周圍的風速變化均較劇烈。最后，三個工況在旋轉域的前面2D和旋轉域的后面3D之間的尾流較為對稱。可能是進口處的空氣進入后遇到具有粘性的風力機葉片之后從一開始的無旋運動轉變為有旋運動導致的流體微團產生了剪切變形和轉動。

圖7 工況一速度云圖（23 m/s, 21.18°）

圖8 工況二速度云圖（18 m/s, 14.92°）

圖9 工況三速度云圖（13 m/s, 6.60°）

3.3.2 工況一旋轉域速度壓力云圖分析

工況一的尾流比較明顯，因此對其進一步分析速度和壓力云圖，其來流風為23 m/s，變槳角度為21.18°。

如圖10～圖13所示，在速度云圖中可以獲知旋轉域中的風力機葉片處的空氣流速明顯低于其他處，有著較為清晰的葉片輪廓，背面葉片輪廓比正面更加明顯，可能是由于葉片背風面邊界層的厚度較大，使得粘性區域也增大；由于輪轂處屬于鈍體繞流所以背面中心點處風速較低；變槳風使得旋轉域的風速一邊高一邊低，可能是由于傾斜的葉輪對空氣具有一定的粘性切割作用，將來流風大體分成兩塊風速區，最終呈現出圖中效果。

圖10 旋轉域正面速度云圖

圖11 旋轉域背面速度云圖

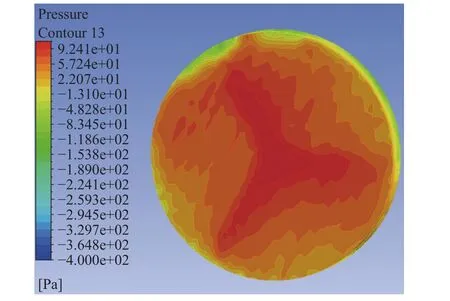
圖12 旋轉域正面壓力云圖

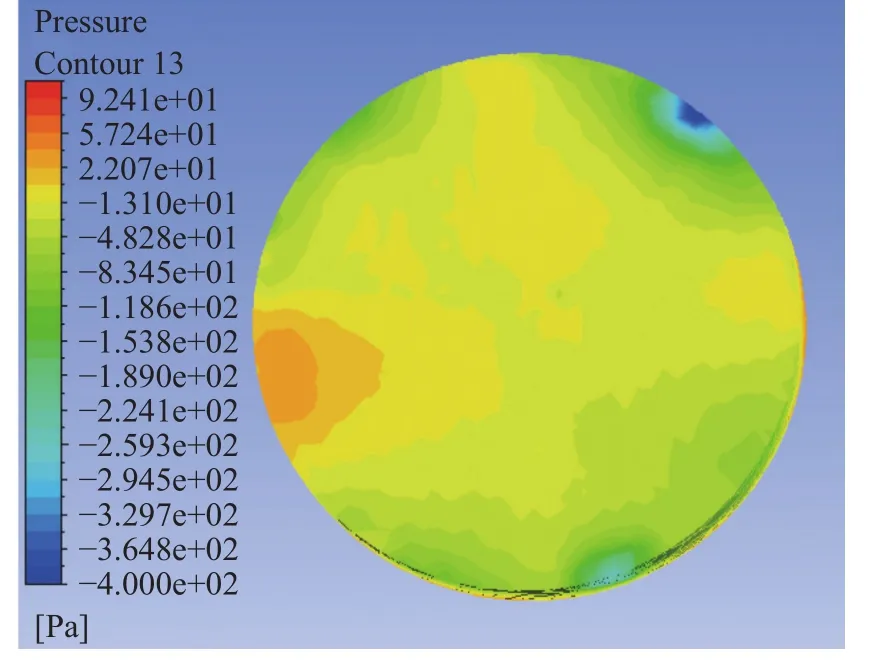
圖13 旋轉域背面壓力云圖

在壓力云圖中風力機的輪廓已經幾乎看不到了，在風力機周圍氣壓比較高，沒有風力機葉片的形狀了，壓力圖較為發散，旋轉域的周圍存在低壓漩渦，正面的壓力明顯比背面的要高。可能是由于迎風面阻力為摩擦阻力和壓差阻力之和，從而導致的旋轉域正面壓力較大。在背風面可能是由于邊界層是分離的，使得粘性剪切力很小，從而導致旋轉域背面壓力較小。

3.3.3 截面面云圖分析

下列各圖風力機所在基準面后的速度云圖，在6D距離之后的速度均為23 m/s，并無分析的價值，因此不再這里概述。

如圖14～圖19所示，由上述的速度云圖可以得知，隨著到風力機的距離增加，空氣的流速越來越接近來流風速，受到風力機的影響越來越弱。在近尾流區（1D～2D）中風速受到風力機的影響風速十分紊亂，都是大致為一個矩形的高風速包圍著不規則的低風速區，在3D～4D距離處，風力機的正后方還能呈現出一定區域的高速區，在左側方向都有一定的高速區域。在遠尾流區（5D～6D）處風速的差別變得非常小，6D之后的風速已經和來流風速一樣，這也進一步證明了計算域足夠大，計算結果具有較高的準確性。由于受到變槳風的作用，左邊的風速均比右邊要高，并且越靠近風力機越明顯。風力機后面的空氣一開始十分紊亂，當4D距離處達到臨界點，空氣的流速開始越來越趨近于來流風速。

圖14 1D速度云圖

圖15 2D速度云圖

圖16 3D速度云圖

圖17 4D速度云圖

圖18 5D速度云圖

圖19 6D速度云圖

3.3.4 截面壓力云圖分析

如圖20～圖23可得，在1D～2D距離時，氣壓比較大，受到風力機尾流影響明顯，1D處大致為一較大的圓形的低壓漩渦，由于變槳風的作用，左邊伴隨有兩個較小的高壓區域；2D處氣旋有一分為二的趨勢，存在著高壓漩渦和低壓漩渦，可能是輪轂處的鈍體繞流引起的高壓漩渦，低壓漩渦可能是由于不平衡的壓差力造成的；在3D處出現轉折點，此處的風壓的差值開始變小，層次感開始清晰，風力機的尾流影響在此處開始明顯減弱。

圖20 1D壓力云圖

圖21 2D壓力云圖

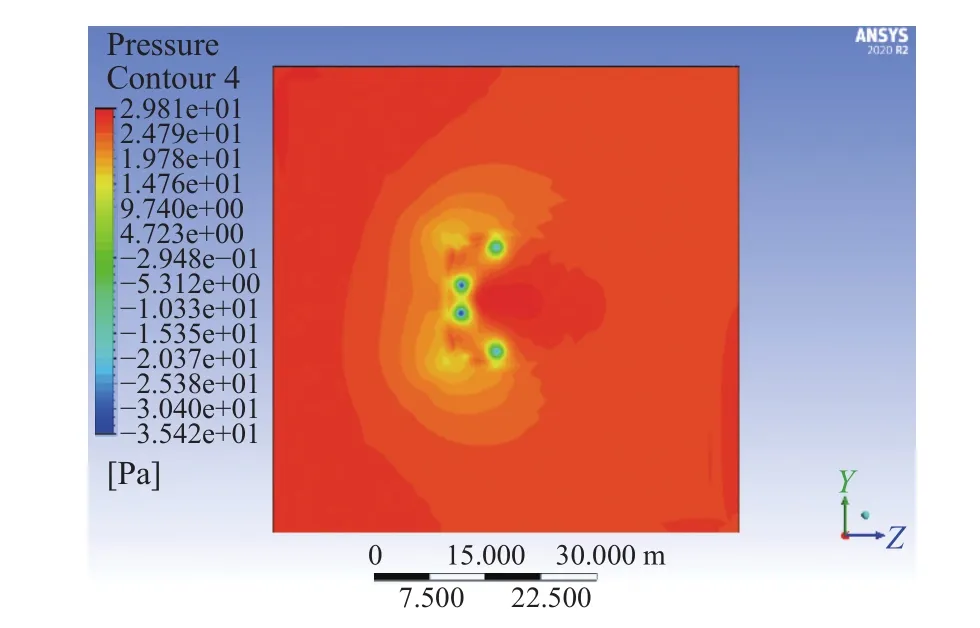
圖22 3D壓力云圖

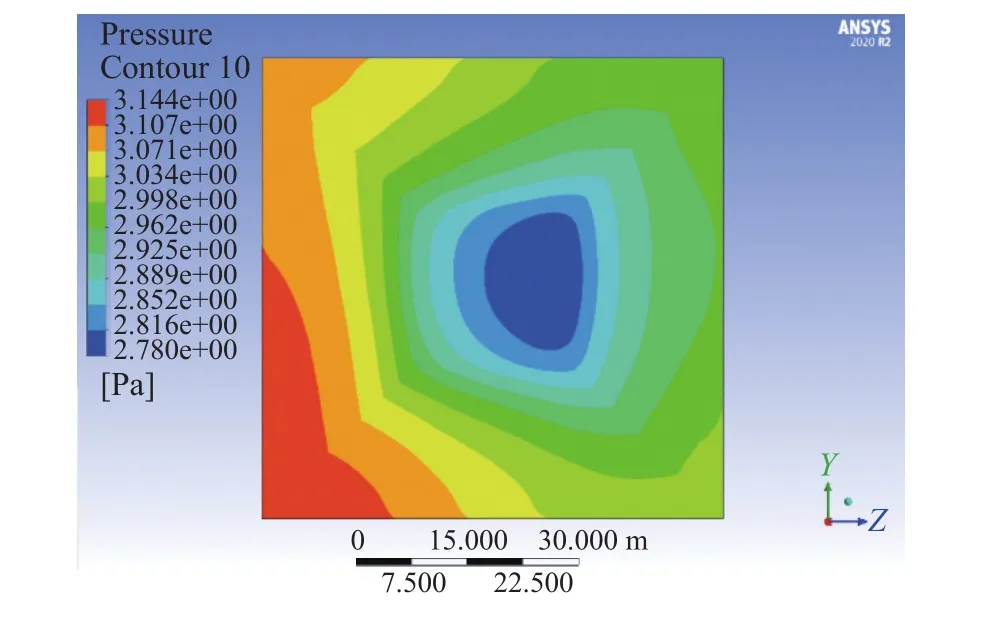
圖23 9D壓力云圖

4 結束語

1） 隨著變槳角和來流風速的增加，風力機的尾流影響的距離越遠，尾流均在4D左右就開始明顯變弱，并且在風力機旋轉域周圍的風速變化均較劇烈和對稱。建議在大型風力機工作時設定的安全距離為4D以上，并且在風速較大時風力機自動停止工作。

2） 在旋轉域中風力機葉片背風面的層流邊界層的厚度較大，從而使得粘性區域也較大，這可能使得速度云圖中有著較為清晰的葉輪輪廓；但是壓力云圖中壓力差較小形成不出葉輪輪廓，并且正面的空氣流速和空氣壓 力均大于背面。建議在工程中加強風力機迎風處的材料強度。

3） 受到變槳的作用，外流域尾流中左側（-Z方向）的空氣流速和空氣壓力較右側（+Z方向）要高一些，并且距離風力機越遠越趨近來流風風速同時空氣流速差也越來越小。