基于反演法的移動機器人軌跡跟蹤控制
高繼勛, 黃全振, 高振東, 趙媛媛
(1. 河南工程學院計算機學院,河南 鄭州 451191; 2. 河南工程學院電氣信息工程學院,河南 鄭州 451191;3. 鄭州工程技術學院,河南 鄭州 450044)
0 引 言
隨著人工智能迅速發展,機器人技術也隨之成為當今研究的熱點[1]。輪式移動機器人作為機器人的一部分,因其靈活、承載能力大等特點,已被普遍應用于軍事、工業、農業等方面[2-3]。
輪式機器人作為一個典型的非線性強耦合控制系統[4],其運動控制模型的建模需要從運動學和動力學兩方面進行綜合分析與設計。軌跡跟蹤作為移動機器人運動控制的核心問題,已有很多研究成果,包括反演控制[5]、反饋線性化[6]、滑模控制[7]等,都是基于模型的非線性控制設計的軌跡跟蹤控制系統,并且取得了廣泛的應用。Kanayama在Lyapunov第二方法的基礎上設計了局部穩定的軌跡跟蹤控制器。在此基礎上,吳衛國[8]利用反演控制法,設計了全局漸進穩定的軌跡跟蹤控制器,但該控制器無法同時完成軌跡跟蹤與鎮定控制。陳罡[9]在此研究基礎上,通過滑模控制與反演控制相結合的方式,完成軌跡跟蹤控制。目前,移動機器人的軌跡跟蹤控制以多種控制方法相結合為發展趨勢,以期望能獲得更好的穩定性和魯棒性。在實際應用過程中,大多數學者的研究是在運動學基礎上展開[10],運動學模型在面對高速、重載的情況控制精度無法達到要求,并且系統穩定性無法保證,因此動力學模型的研究對于移動機器人應用具有重要的學術意義和工程價值[11]。
本文基于移動機器人的動力學模型,通過對模型的解耦和分析,利用反演控制方法設計控制律,依據Lyapunov證明系統的穩定和跟蹤誤差的收斂最終完成移動機器人對理想軌跡速度、角度的跟蹤任務。
1 模型建立推導
本文以兩輪差速移動機器人為研究對象,且在二維平面內運動時只有滾動、無滑動。移動機器人的模型如圖1所示。

圖1 兩輪差速移動機器人模型
2l為車身寬度,r為輪胎半徑,P為移動機器人的質心。為航向角,的方向為移動機器人線速度方向,始終垂直于車輪之間連線,、為左輪和右輪轉角,速度矢量可表示為。由文獻[12]可知,在o-xy絕對坐標系內,可用動力學方程描述移動機器人動態特性。
根據力矩平衡原理和牛頓定律,對移動機器人及車輪進行分析。


2 控制器設計
反演控制的設計思路是從一個高階系統開始,在保證系統性能的前提下,將一個非線性系統分解為相應的低階子系統,然后在子系統中設計相應的控制量。本文通過反演控制方法,分別對線速度和角度進行控制律設計。
定義Lyapunov函數V0:

3 仿真實驗與結果分析
為驗證控制算法的有效性,分別使用計算機仿真軟件Matlab數值仿真和硬件平臺構建模擬/物理實驗系統進行驗證。
3.1 數值仿真
系統狀態方程如式(12)所示,選取控制對象為式 (13)、(14),選取系統參數從而可得到系統參數
取參考軌跡,理想線速度vd=1.0 m/s, 理想角度φd=sintrad 。系統參數k1=k2=k3=10,仿真結果如圖2、圖3所示。

圖2 線速度跟蹤和角度跟蹤曲線

圖3 仿真軌跡曲線
圖2中,紅色實線分別表示理想線速度和角度,藍色實線分別表示實際線速度和角度。圖3為仿真軌跡曲線。由圖2可以知,在一定時間內,實際線速度與角度逐漸趨近于理想線速度和角度,并最終保持一致,完成跟蹤任務。系統在控制律約束下,仿真軌跡如圖3所示。
3.2 實驗驗證
硬件實驗平臺部分主要由雙輪差速驅動底盤Turtlebot2、IMU模塊、GPS差分定位模塊(RTK)和主計算機(Jetson Nano)構成,如圖4、圖5所示。

圖4 實驗平臺實物圖

圖5 實驗平臺示意圖
Turtlebot2底盤包括ST微控制器,霍爾編碼器(500線)和兩個直流電機,電機通過微控制器的兩個脈寬調制通道獨立控制,同時為左、右電機產生控制信號。IMU模塊為九軸姿態傳感器,可完成對移動機器人航向角、加速度數據的采集,采樣頻率為20 Hz。GPS差分定位模塊(RTK)定位準確度為5 cm,采樣頻率為5 Hz,并且通過主計算機控制程序實時完成位置記錄。主計算機(Jetson Nano)運行Ubuntu操作系統,通過串口與微控制器通信,包含左、右電機速度的信息、移動機器人姿態信息和定位信息。
主計算機通過傳感器RTK和IMU完成對移動機器人位姿數據的采集。控制系統通過傳感器采集到的數據,對移動機器人下一時刻運動狀態進行計算,之后輸出對應控制參數給電機驅動,完成對移動機器人運動狀態的控制,流程圖如圖6所示。

圖6 移動機器人系統控制流程圖
首先,使用移動機器人完成對期望軌跡數據的采集,離線處理后保存到移動機器人主計算機。實驗過程中,移動機器人通過對期望軌跡與當前位置誤差的計算,得到所需要的控制輸入。在移動機器人運動的同時,主計算機會實時將數據保存在本地。由于Nano(2 GB內存)硬件內存不足的原因無法完成位姿在線顯示的任務,因此只能通過離線的方式對保存在本地的數據進行處理。
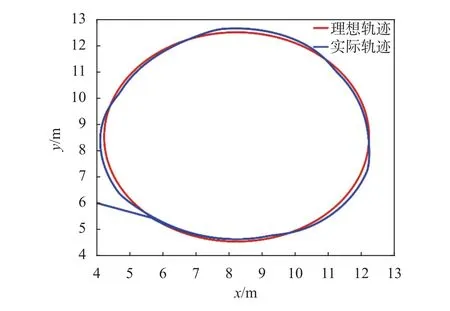
圖7 動力學模型實驗軌跡跟蹤曲線

圖8 動力學模型位置誤差曲線

圖9 動力學模型速度曲線
由圖7可知,紅色實線為理想軌跡,藍色實線為實際軌跡,在一定時間內,移動機器人可完成對理想軌跡的跟蹤任務。圖8為移動機器人實際運動軌跡與理想軌跡隨時間變化的誤差曲線,誤差由初始2 m逐漸減小,最終穩定在0.2 m左右。
為驗證本文方法的有效性,使用文獻 [12]中以運動學模型為對象的控制方法。同樣選取軌跡為半徑的圓,令理想線速度,理想角度。移動機器人初始位置為[7 10.5]。實驗結果如圖10、圖11、圖12所示。

圖10 運動學模型軌跡跟蹤曲線
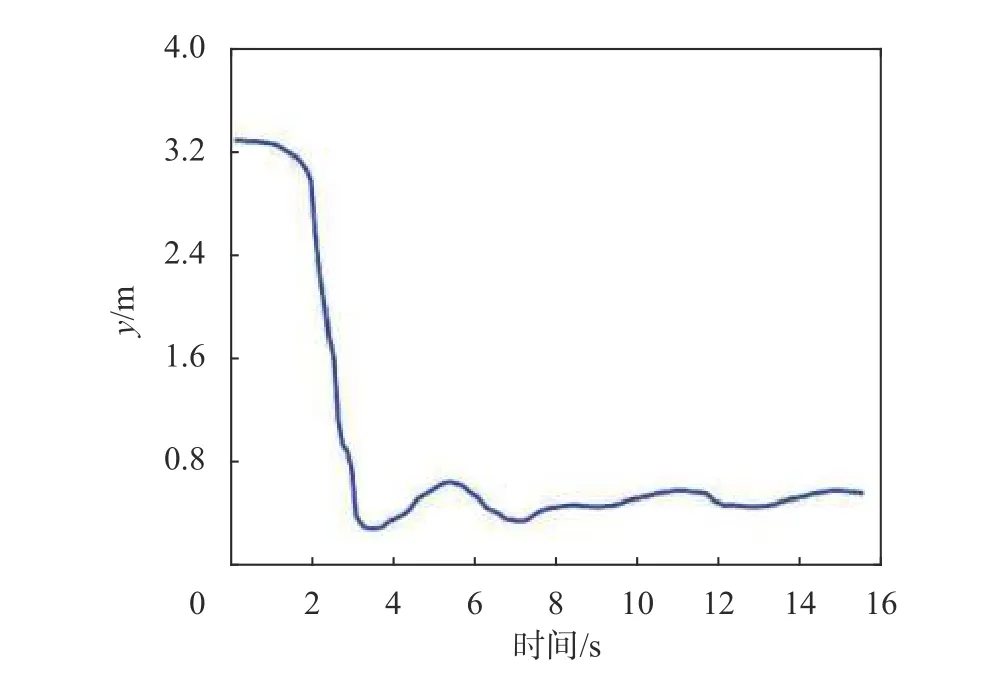
圖11 運動學模型位置誤差曲線

圖12 運動學模型速度曲線
在圖10中,紅色實線為理想軌跡,藍色實線為實際軌跡。圖11為移動機器人實際運動軌跡與理想軌跡隨時間變化的誤差曲線,最終穩定在左右。圖9所示為移動機器人速度曲線。
將圖7、圖8與圖10、圖11對比可知,動力學模型下,移動機器人誤差收斂迅速,并且達到收斂速度后較為穩定、誤差較小,同時運動軌跡較為平滑。對比圖9與圖12,動力學模型下,移動機器人響應速度更快,并且控制精度更高;運動學模型下,速度曲線波動較大。
以相同實驗對象為前提,對比不同控制模型的實驗結果,動力學模型下的移動機器人跟蹤誤差由0.5 m減小到0.2 m左右,提高了控制精度和準確度更高,同時減小了結構非線性特性的影響,使系統具有更好的穩定性和魯棒性。
4 結束語
本文根據兩輪差速移動機器人模型的運動特征和受力情況,建立動力學模型。針對實際應用問題,對模型進行解耦和分析,利用反演控制方法將控制系統分解為線速度控制和角度控制,分別對移動機器人的速度和角度跟蹤進行控制律設計,并利用Lyapunov穩定性理論證明系統的穩定。
通過數值仿真算例,驗證了該系統的有效性與穩定性,并且能夠保證速度和角度跟蹤的精度、收斂速度。最后通過實驗,表明了該控制方法在實際應用中的可行性,為以后的研究工作提供了一定的參考和借鑒。

