MMPC-Tabu混合算法的貝葉斯網絡模型在高脂血癥相關因素研究中的應用*

王旭春 宋偉梅，2 潘金花 任 浩 張 壯 翟夢夢 陳利民 仇麗霞△

【提 要】 目的 本研究采用MMPC-Tabu混合算法構建山西省高脂血癥的貝葉斯網絡模型，研究高脂血癥及其相關因素間的網絡關系及相關程度，并通過貝葉斯網絡對高脂血癥進行患病風險推理，為慢病影響因素分析提供更合理的建模方法。方法 采用logistic回歸對山西省18歲以上居民高脂血癥的調查數據進行變量初步篩選，再以MMPC-Tabu混合算法和極大似然估計法構建貝葉斯網絡。結果 2013年山西省高脂血癥患病率為42.6%(95%CI：41.1%～44.1%)。將logistic回歸初篩與高脂血癥有關的9個變量，采用MMPC-Tabu算法構建高脂血癥的貝葉斯網絡模型，結果顯示：中心性肥胖和BMI與高脂血癥直接相關，是高脂血癥的父節點，即它們與高脂血癥的發生有關；高血壓、身體活動、性別、年齡、地區、糖尿病通過影響中心性肥胖和BMI間接影響高脂血癥的發生。結論 貝葉斯網絡可以反映因素與疾病整體聯動效應，揭示高脂血癥直接和間接相關的因素和關聯強度，同時闡明除高脂血癥以外的其他影響因素間的關系，可為慢性病與相關因素的研究提供合理的方法。

近年來，隨著經濟的迅猛發展，居民生活水平及飲食習慣的改變，血脂異常率不斷上升，2014年中國血脂異常率已高達41.9%[1-2]。血脂升高導致血管粥樣硬化，是促進心腦血管疾病發生和發展的關鍵因素[3]。因此，對高脂血癥的相關因素進行全面分析，揭示因素間復雜的網絡聯系，有針對性地對高脂血癥采取預防控制措施顯得尤為重要。

目前，國內外對高脂血癥的相關因素研究多采用logistic回歸，以優勢比(odds ratio，OR)的大小來反映相關因素對高脂血癥的影響強度。在實際應用中，logistic回歸的變量獨立性假設很難得到滿足，且無法區分高脂血癥的直接或間接相關因素。從醫學生物學角度分析，疾病與病因以及病因之間都可能存在著復雜的網絡聯系，各變量間相互影響，具有整體聯動性，這在傳統logistic回歸中難以體現。而貝葉斯網絡不僅對變量間的獨立性沒有嚴格要求，還可以通過網絡圖和條件概率表來反映因素間的復雜聯動關系及相關程度[4]。另外，在已知某些節點(影響因素)狀態的情況下，貝葉斯網絡還可以利用貝葉斯定理對未知節點(高脂血癥)進行風險推理，彌補了logistic回歸在進行概率預測時需要掌握所有因素狀態的不足[5-6]。相比于logistic回歸，貝葉斯網絡能更為直觀地揭示疾病與病因之間復雜聯動的網絡風險機制，是描述疾病及其影響因素間相關關系的有效方法[7-8]。

貝葉斯網絡的結構學習算法[9]包括基于約束的算法、基于評分搜索的算法以及二者結合的混合算法，約束算法能得到全局最優解，且學習效率較高，但高階條件獨立性檢驗計算復雜且所得結果也不夠可靠。評分搜索算法雖然能彌補前者的一些不足，但易陷入局部最優。因此，有研究者提出了將兩者相結合的混合算法，比較經典且應用較為廣泛的混合算法為Tsamardino等[10]于2006年提出的最大最小爬山(max-min hill-climbing，MMHC)混合算法，該算法結合了最大最小父子集(max-min parents and children，MMPC)算法和爬山法，但爬山法容易陷入局部最優。2015年，課題組成員張雪雷[11]證實了作為全局智能優化算法的禁忌搜索算法(Tabu search algorithm，Tabu)對貝葉斯網絡優化效果優于爬山算法。課題組前期嘗試將MMPC算法與Tabu算法進行結合，建立MMPC-Tabu混合算法，并通過仿真實驗證實了在節點數較多、大樣本的情況下，MMPC-Tabu算法構建貝葉斯網絡的效果優于MMHC算法。

本研究利用山西省2013年高脂血癥及其危險因素監測數據進行分析。首先利用logistic回歸初篩變量，找出主要變量；然后基于MMPC-Tabu混合算法構建高脂血癥及其相關因素的貝葉斯網絡，探究高脂血癥及其影響因素間的網絡結構關系，為慢性病相關因素的研究提供新的網絡構建方法。

資料與方法

1.調查對象

本研究按照國家慢病調查方案，根據山西的地理位置劃分為8個大片區，采用多階段隨機抽樣方法收集樣本。首先在每一個大片區隨機抽取1個區(縣)作為國家慢病監測點，隨后在各個監測點隨機抽取4個鄉鎮、街道或團，在已抽取的鄉鎮、街道或團中隨機抽取3個村、居委會或連，再在抽取的村、居委會或連中隨機抽取50戶居民，按照KISH表法在每戶居民中隨機抽取1位居民(18歲及以上)。

納入標準：調查前在調查點內居住時間超過6個月、年齡≥18歲的居民。排除標準：居住在功能區(工棚、軍隊、學生宿舍、養老院等)內的居民。倫理審查編號為201307。

2.數據收集

采用問卷調查、身體測量、實驗室檢查等方法獲取所需樣本資料。

3.評價標準

(1)高脂血癥：依據《中國成人血脂異常防治指南》[12]中的血脂異常診斷標準；(2)高血壓：依據《中國高血壓防治指南》[13]中高血壓評價指標；(3)糖尿病：指空腹血糖大于等于7mmol/L或2小時餐后血糖大于等于11.1mmol/L，或已被診斷為糖尿病的人；(4)吸煙：指連續6個月日均吸煙量大于等于1支者；(5)身體質量指數BMI低于18.5kg/m2為偏瘦、正常體重在18.5至23.9kg/m2之間、24.0至27.9kg/m2為超重、大于等于28.0kg/m2為肥胖；(6)中心性肥胖：指女性腰圍大于等于80 cm，男性腰圍大于等于85 cm；(7)心率：心率低于60次/min為心動過緩、高于100次/min為心動過速、60至100次/min為正常范圍；(8)身體活動度：以代謝當量的25%和75%為界，將身體活動度分為身體活動不足、達標和充足。

4.統計學處理

采用IBM SPSS 22.0進行統計描述和多因素logistic回歸。利用R 3.5.0中bnlearn package進行貝葉斯網絡結構學習，bnlearn package包含多種貝葉斯網絡學習算法，本文采用MMPC和Tabu結合的混合學習算法。采用Netica可視化貝葉斯網絡，建立推理模型并計算條件概率。Netica是用Java開發的貝葉斯網絡學習工具，能夠高效地建立貝葉斯網絡拓撲結構，并可根據先驗知識及更新的知識進行傳遞和積累，適用性強，可視化操作方便。先驗概率分為基于歷史資料獲得的客觀先驗概率和根據主觀經驗判斷得到的主觀先驗概率，本文采用客觀先驗概率，極大似然法估計條件概率。

5.MMPC-Tabu混合算法概述

MMPC-Tabu結構學習算法分為兩個階段，第一階段采用MMPC[14]算法獲得貝葉斯網絡框架；第二階段利用禁忌搜索算法確定網絡邊及其方向，建立完整的貝葉斯網絡結構。

MMPC算法為基于約束的啟發式算法，也分為兩個階段：(1)采用Max-Min啟發式搜索方法獲得每個節點的候選父子節點集(candidate parents and children，CPC)，同樣利用該搜索方法計算其余所有變量與目標變量T之間的最小關聯度值，從中選擇關聯度最大的一個變量進入CPC，在CPC中全部子集都給定的條件下，若其他節點都獨立于T，該階段結束；(2)通過條件獨立性測試函數Ind(X；T|Z)移去CPC中第一階段誤入的變量。若CPC中存在X，使Ind(X；T|Z)成立，其中Z∈CPC，即變量X與目標變量T在已知Z時具備獨立性關系，則將X移出CPC。

禁忌搜索算法[15](Tabu算法)模擬人類大腦的短期記憶功能進行搜索，屬于全局智能優化的搜索算法，具有參數少、結構簡單和全局尋優能力強等特點。在網絡框架中，執行加邊、刪邊、逆向邊操作，通過禁忌表和局部鄰域移動機制來避免重復搜索，以此加快搜索進程，并利用藐視準則來激活那些被納入禁忌表的優良狀態，通過在多鄰域方向進行有效探索，使搜索范圍跳出局部最優，最終得到全局的最優解。

MMPC- Tabu混合算法結合了MMPC算法和禁忌搜索算法，與經典的MMHC算法相比，MMPC- Tabu算法在搜索階段進行了改進，采用禁忌搜索使得搜索過程跳出了局部最優，彌補了MMHC算法搜索階段的不足。

結 果

1.人群基本特征及血脂異常率

本研究共調查4776人，資料整理后保留完整數據4105例，保留可能與高脂血癥發生相關的17個變量，變量及其賦值詳見表1。

2.高脂血癥多因素logistic回歸

采用logistic逐步回歸對原始數據所保留的17個變量進行變量篩選，其中α入取0.10、α出取0.15，確定顯著相關因素，以簡化后期的貝葉斯網絡模型。

多因素logistic逐步回歸的分析結果顯示：性別、地區、身體活動度、BMI、中心性肥胖、高血壓和糖尿病7個變量與高脂血癥顯著相關。男性患高脂血癥的風險相比于女性升高了38.3%；農村居民患高脂血癥的風險相比于城市居民升高了15.2%；BMI每增加一個等級，患高脂血癥的風險增加47.1%；中心性肥胖者患高脂血癥的風險較非中心性肥胖者增加70.2%，身體活動度每增加一個等級高脂血癥的患病風險降低11.5%，合并糖尿病和高血壓者患高脂血癥的風險相比于血糖、血壓正常者，分別升高了30.7%和26.7%，詳見表2。

3.高脂血癥的影響因素間的關聯性分析

logistic回歸在基于變量獨立的前提假設下，可以找出與高脂血癥顯著相關的獨立影響因素，但一般情況下，各影響因素間往往相互關聯，由表3、4中不同年齡、性別與BMI、中心性肥胖和身體活動度的相關分析以及高血壓、糖尿病與高脂血癥其他影響因素間的差異性檢驗可知，年齡、性別與BMI、身體活動度和中心性肥胖有關(P<0.05)；BMI、中心性肥胖、年齡、地區等因素均與高血壓、糖尿病相關(P<0.05)，身體活動度與高血壓之間的差異也存在統計學意義。說明高脂血癥的影響因素間并不互相獨立，且存在復雜的網絡聯系。

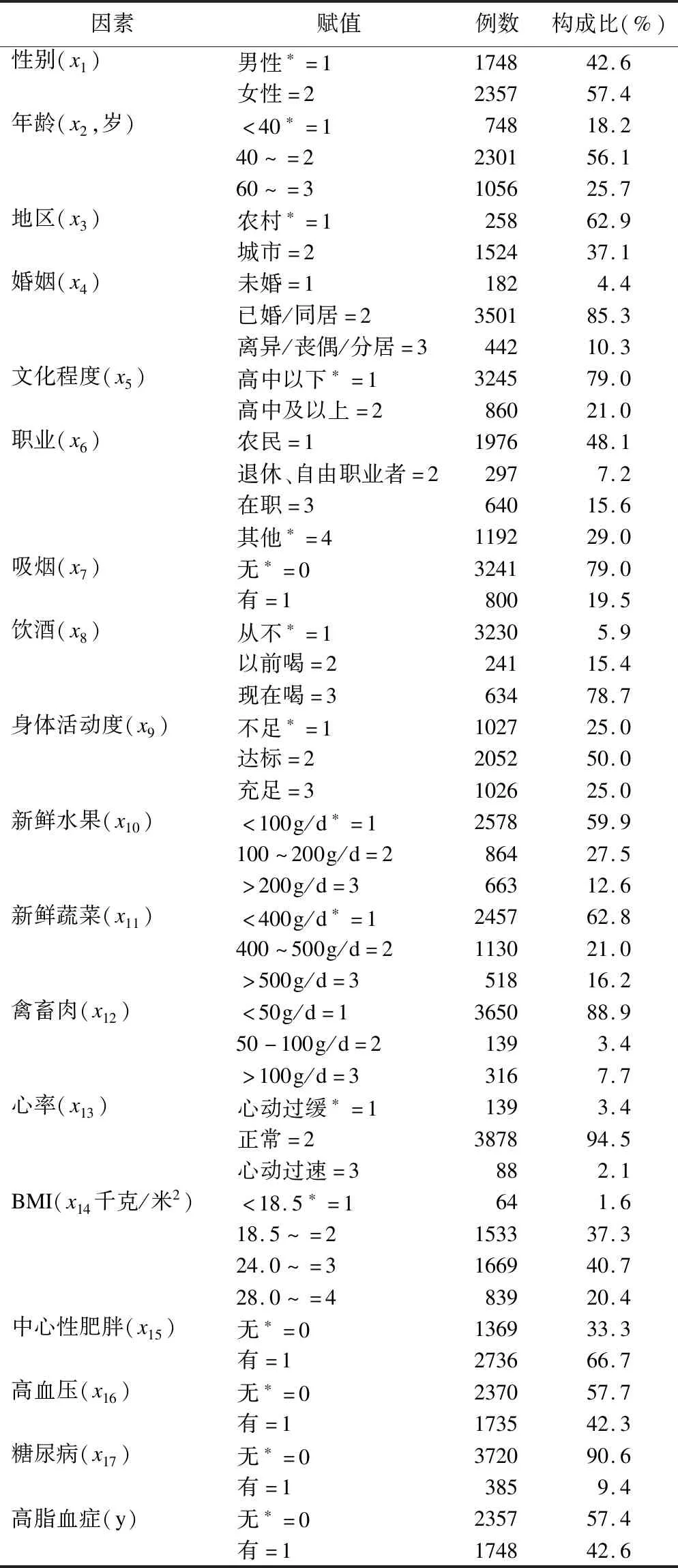
表1 變量賦值及構成比

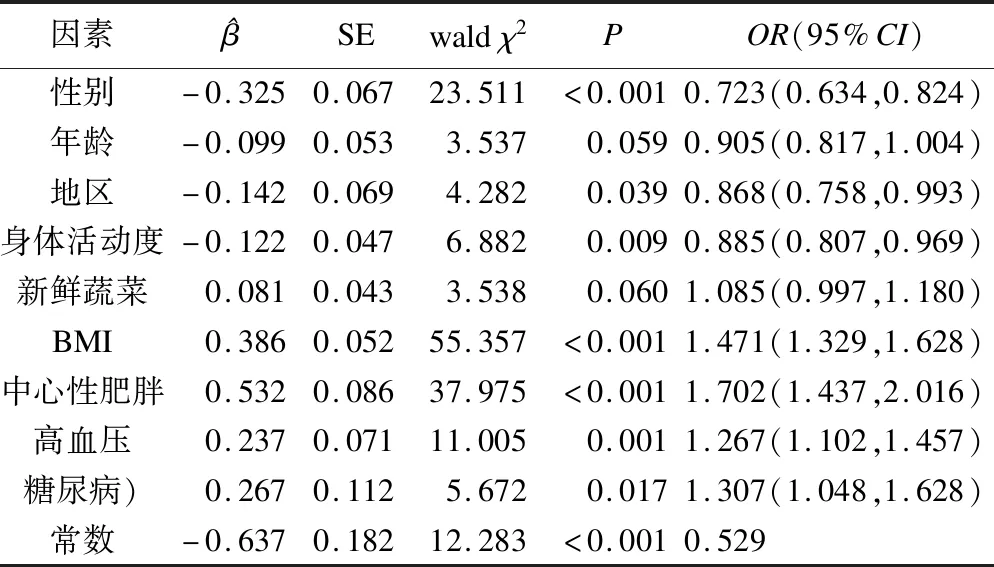
表2 高脂血癥的logistic回歸分析

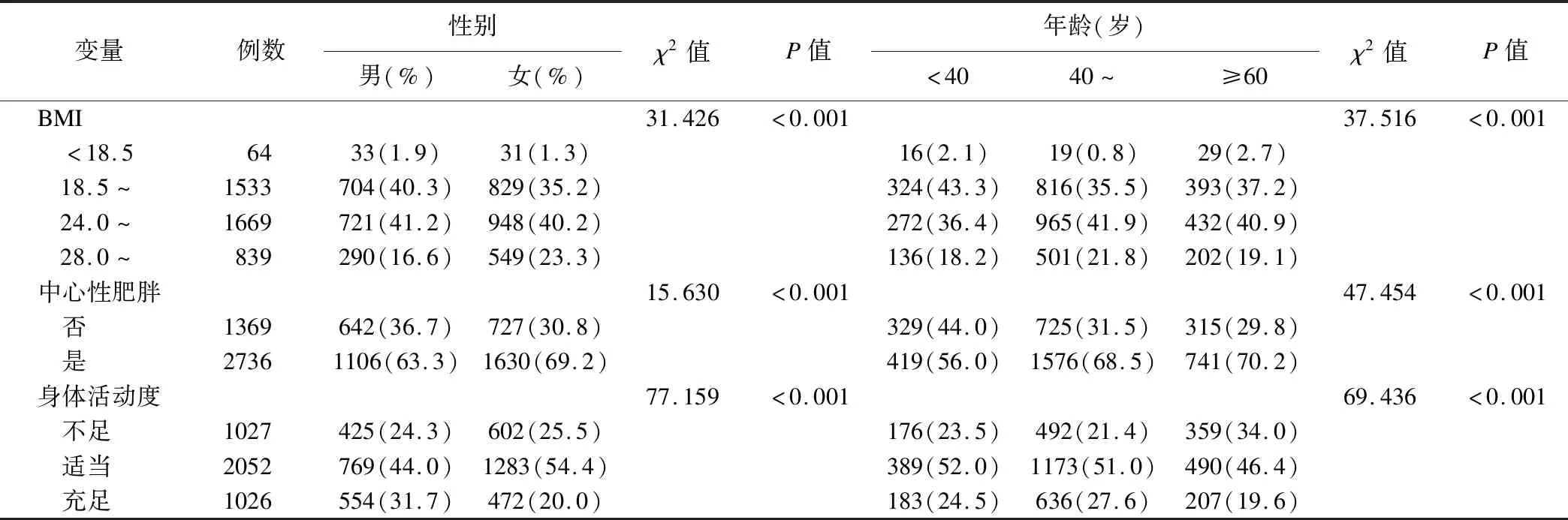
表3 不同年齡、性別與BMI、中心性肥胖和身體活動度的關系

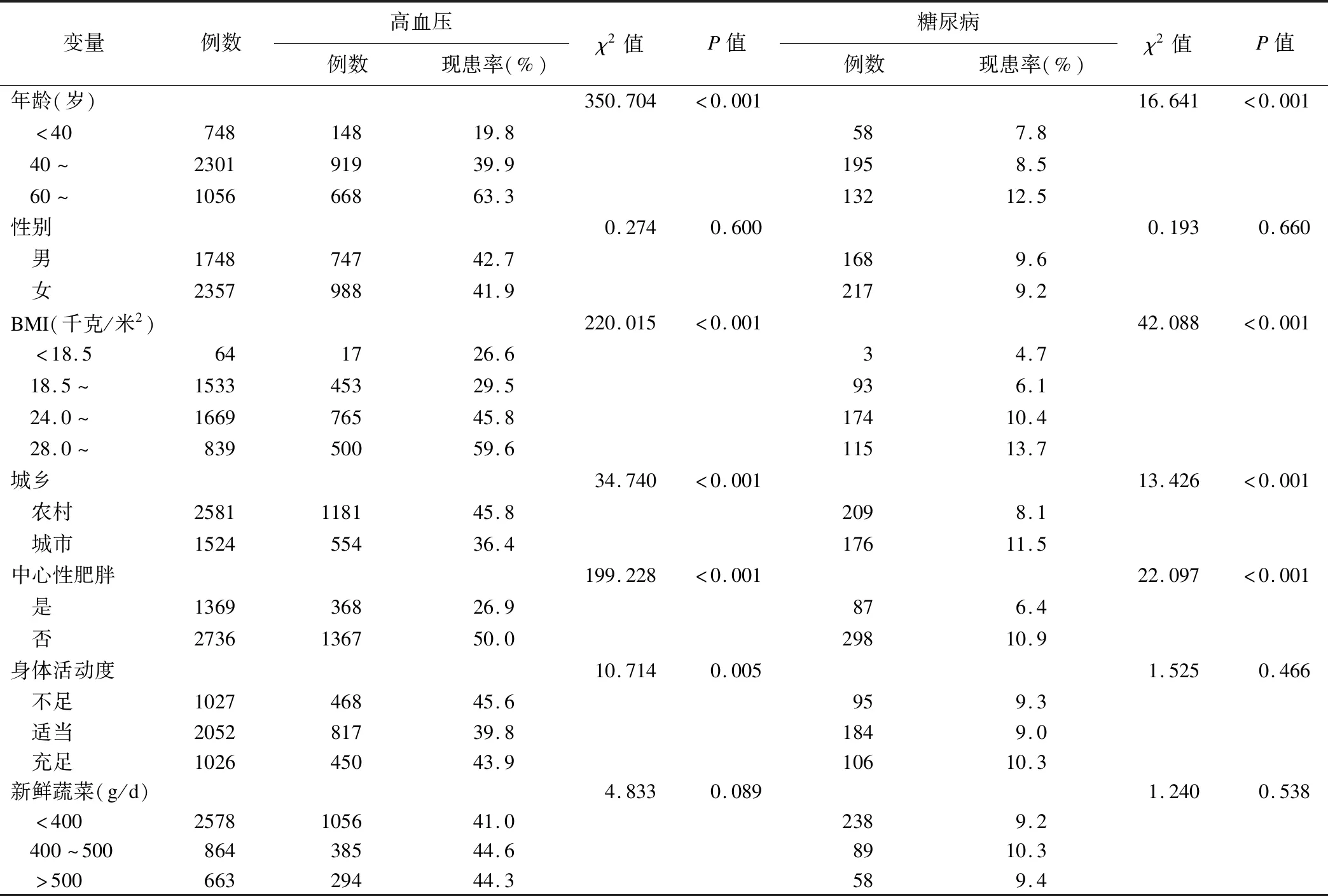
表4 高血壓、糖尿病與高脂血癥其他影響因素的關系

4.高脂血癥的貝葉斯網絡模型

將logistic回歸中以α入取0.10、α出取0.15為準篩選的9個變量，采用MMPC-Tabu混合算法和極大似然估計法構建高脂血癥及其相關因素的貝葉斯網絡和條件概率表(圖1)。圖中節點方框中的數值與矩陣條代表的是各節點的先驗概率，例如高脂血癥的患病組對應數值為42.6，表示患高脂血癥者在全部人群中所占比例為42.6%，為該節點的先驗概率。有向弧表示變量間的條件依賴關系。由圖可知，中心性肥胖和BMI與高脂血癥直接相關，為高脂血癥的父節點，直接影響著血脂的變化，高血壓、身體活動、性別、年齡、地區、糖尿病通過影響中心性肥胖和BMI與高脂血癥間接相關。

貝葉斯網絡還可以描述性別、年齡、地區、身體活動、高血壓、糖尿病這些除高脂血癥之外的影響因素間存在著的復雜網絡關系。如貝葉斯網絡提示高血壓與BMI、年齡、地區有關，在表2中也顯示隨著BMI值、年齡的增加，高血壓的檢出率隨之增加，農村居民的高血壓患病率高于城市居民；年齡和性別與身體活動度之間直接相關，且通過網絡間接影響BMI和中心性肥胖，這與表3中顯示的不同年齡、性別與BMI、中心性肥胖和身體活動度有關的結論相一致。充分說明貝葉斯網絡能很好地揭示疾病與病因，以及病因之間復雜的網絡聯系。

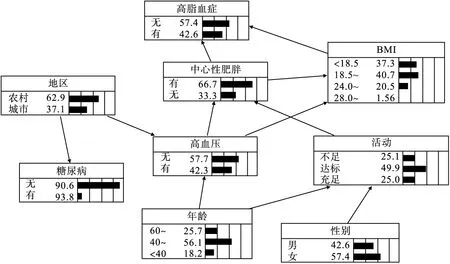
圖1 最大最小父子集——禁忌搜索混合算法構建高脂血癥貝葉斯網絡及先驗概率

5.高脂血癥的風險推理

表5是高脂血癥節點的條件概率分布表，可以看出高脂血癥與其兩個父節點中心性肥胖和BMI之間的概率依賴關系。當某人BMI在正常范圍(18.5～24.0kg/m2)且體型正常時，其患高血脂的風險為0.26416；當其體型正常，BMI>28.0kg/m2時，患高血脂的風險提高到0.41736；而當其屬于中心性肥胖且BMI>28.0kg/m2時，其發生風險提高到了0.57315。

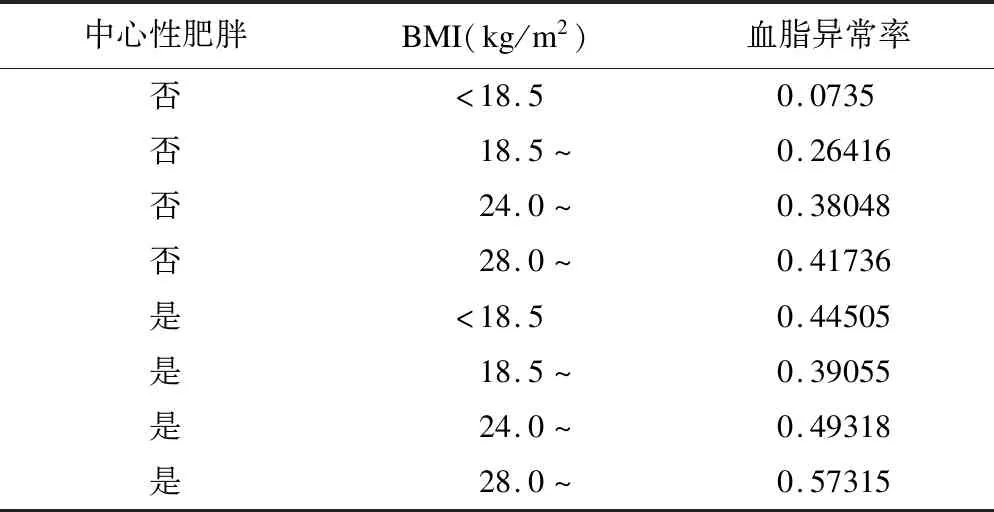
表5 高血脂癥節點的條件概率表

貝葉斯網絡還可以進行因果推理，即根據已知節點的信息對未知節點進行概率預測，繼而對高脂血癥進行風險推理。若已知某人為中心性肥胖而無其他病史，通過貝葉斯網絡推理可知，其患高脂血癥的可能性為0.498(圖2)；若其僅患有高血壓，患高脂血癥的可能性為0.461(圖3)；如果該個體在中心性肥胖的基礎上還患有高血壓，則患高脂血癥的可能性增加到0.508(圖4)。

討 論

貝葉斯網絡也被稱為概率圖模型，是依據概率值進行不確定性推理的方法，通過構建網絡圖的形式反映多個變量間相互聯系，以條件概率的形式反映變量間的關聯強度，能直觀地展現高脂血癥及其相關因素間復雜的網絡關系。貝葉斯網絡提示，中心性肥胖和BMI與高脂血癥直接相關，是高脂血癥的父節點，直接影響著血脂的變化，其中高血壓、身體活動、性別、年齡、地區、糖尿病通過影響中心性肥胖和BMI間接對血脂產生影響。這些研究結果與現有的醫學知識相符。因此，適度鍛煉、注意控制體重和腰圍，可以降低高脂血癥的風險，在此基礎上也可以降低高血壓的風險。由此可見，貝葉斯網絡可以很好地刻畫各因素間、因素與高脂血癥間復雜的網絡關系，可以識別與高脂血癥直接相關和間接相關的因素，對于斷面調查數據可以給出因果關系的提示，便于全面深入發掘因素間的內部關系，能主次分明地提出高脂血癥的預防策略。同時，由于貝葉斯網絡研究變量間的關系時，沒有輸入和輸出變量，因此，它還可以描述其他因素間的關系。這些是logistic回歸分析所不能達到的。

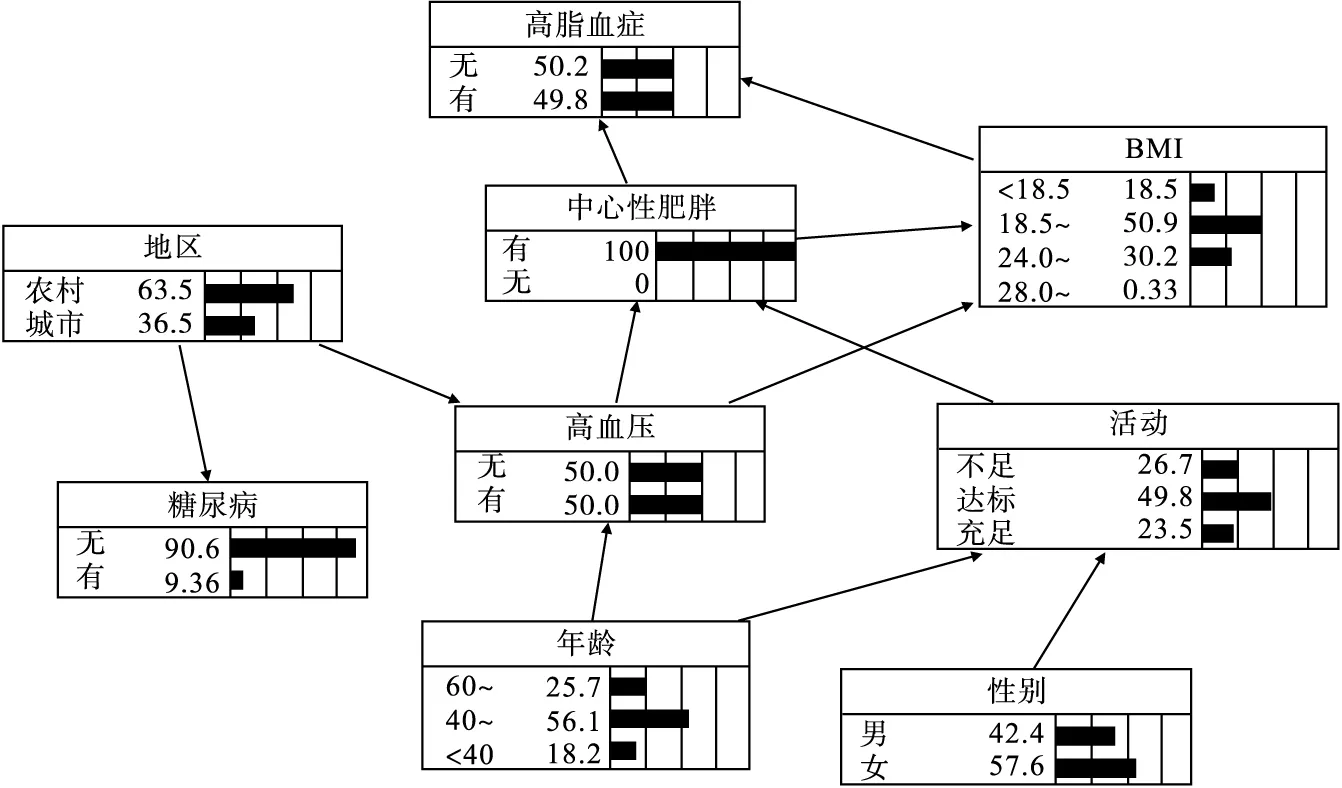
圖2 中心性肥胖時血脂異常的風險推理

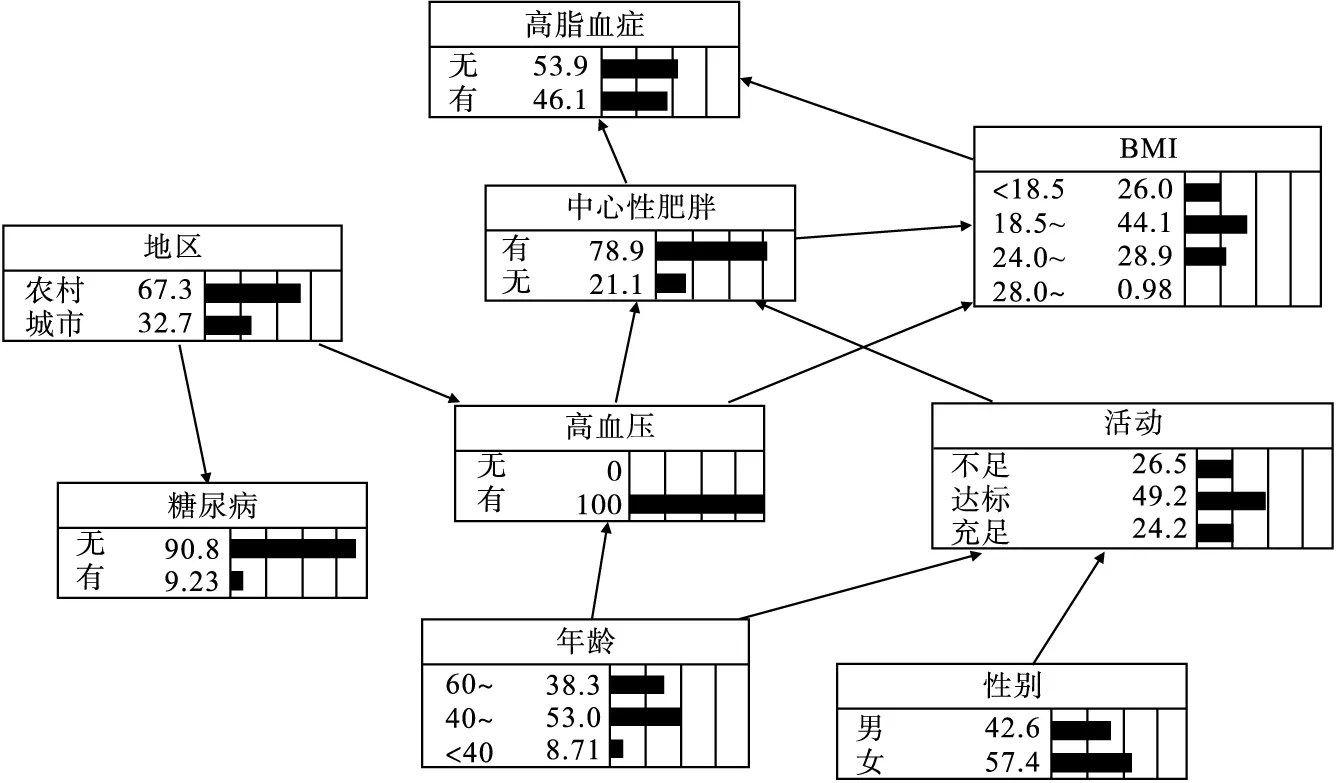
圖3 患高血壓時患高脂血癥的風險推理

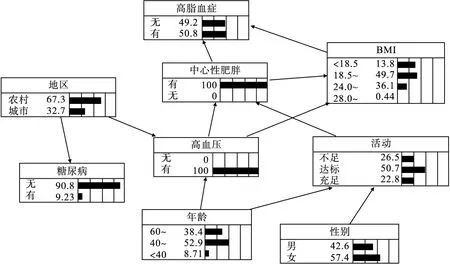
圖4 患高血壓且為中心性肥胖時患高脂血癥的風險推理

貝葉斯網絡還能根據已知節點的狀態來推斷未知節點的概率，從而對高脂血癥進行風險推理。某個體患高脂血癥的先驗概率為P高脂血癥=0.426，若某個體患有高血壓，其患高脂血癥的可能性為P(高脂血癥|高血壓)=0.461，風險提高了3.5%；如果患有高血壓的同時還屬于中心性肥胖，則患高脂血癥的可能性變為P(高脂血癥|高血壓，中心性肥胖)=0.508，風險進一步提高了8.2%。由此可見，貝葉斯網絡可以進行序貫推理，根據某因素條件概率的變化，評價該因素的風險強度，說明其在預防工作中的價值；另外，從風險推理的過程中也能看到，若某一因素變化，網絡中其他因素不同水平的條件概率隨之發生改變，體現了事物的整體聯動性，換句話說，貝葉斯網絡反映因素與疾病的整體聯動性，并不區分主效應或交互效應，更能客觀、全面地描述因素與疾病的關聯強度。而logistic回歸是不能進行序貫推理的，也不能反映因素與疾病的整體聯動性。

由于貝葉斯網絡建模時對樣本量的需求較大，同時對構建過于復雜的網絡結構不太適用，只要抓住主要的因素就達到了研究目的。因此，實際工作中，可以先采用logistic回歸分析對變量進行初篩，再構建貝葉斯網絡，以深入地描述變量間的關系。

綜上所述，本課題基于MMPC-Tabu算法構建的高脂血癥貝葉斯網絡可以合理地描述高脂血癥與各變量間的關系，該算法構建的慢性病貝葉斯網絡的研究成果尚未見報道。因此，本課題將為慢性病與相關因素的研究提供更合理的方法。