印制電路板射頻線圈的部分元等效電路研究

徐顯能 徐 征

印制電路板射頻線圈的部分元等效電路研究

徐顯能 徐 征

（重慶大學電氣工程學院 重慶 400044）

印制電路板（PCB）射頻線圈具有性能優良、占用空間少且制作工藝簡單的特點，常用于無線電能傳輸以及單邊核磁測井等領域。為分析線圈性能，需計算交流電阻、電感以及射頻磁場分布。由于PCB線圈銅線厚度與外圍尺寸跨度大，尤其在考慮金屬渦流時，常規有限元軟件與解析法在處理這種多尺度電磁場問題時的計算速度與精度無法達到要求。在0.5～15MHz頻率范圍內，該文采用部分元等效電路（PEEC）法計算金屬渦流下PCB線圈（銅厚為35μm）的阻抗與射頻磁場分布。建立平面矩形螺旋PCB線圈的PEEC模型；通過計算結果與實測結果對比，總結給出PEEC剖分參數選取方法；分析PEEC模型下線圈的磁場分布；最終實現金屬渦流下PCB線圈的阻抗與射頻磁場的準確且快速計算。該文工作可為應用于無線電能傳輸以及單邊核磁測井等領域的PCB線圈分析提供參考。

部分元等效電路 PCB線圈 多尺度 交流電阻 渦流

0 引言

平面印制電路板（Printed Circuit Boards, PCB）射頻線圈采用印制電路板技術，占用空間少且質量穩定可靠，常應用于無線電能傳輸以及單邊核磁測井等領域[1-6]。例如，用于核磁測井的PCB線圈的銅線厚度通常為幾十μm，橫截面寬度在mm級別，而整個線圈外圍尺寸則能達到cm甚至m的級別。尤其當考慮金屬渦流時，整個線圈模型是一個明顯的多尺度電磁場問題。分析PCB線圈性能與設計線圈結構，首先需要準確且快速地計算其交流電阻、電感以及射頻磁場分布。

高頻下，PCB線圈銅線橫截面的電流密度分布不均勻，影響PCB線圈電磁參數的因素主要包括趨膚效應、鄰近效應以及金屬的渦流效應。例如，在頻率為8MHz下，趨膚效應使得銅線的趨膚深度僅為23.6μm，且頻率越高，銅線由表及里的電流密度衰減越快，要準確且快速計算多尺度PCB線圈電磁參數十分困難[7-8]。

高頻下PCB線圈電磁參數的計算方法主要有三種：①解析法[9-10]，目前只針對一些簡單的線圈結構有解析解表達式，尤其針對渦流場的求解是所有電磁場解析求解中最困難的；②有限元法[6, 11-12]，在求解過程中，除了模擬目標區域之外，還需要對背景區域一起模擬，很大程度上降低了求解效率；③細絲法[13]，是一種忽略時間延遲效應，且由電阻和電感效應為主導的簡化計算方法。高頻下，由于平面線圈自身的電容效應，以及介質基片所帶來的耦合電容等影響，導致細絲法計算電阻的誤差越來越大。

部分元等效電路（Partial Element Equivalent Circuit, PEEC）法由于無需對背景空氣域進行剖分，且能將電磁問題自然地解釋為一個純電路問題，便于分析局部元件的特性，已被證明非常適用于互連線[14]和天線[15]等電磁裝置的分析。但是，目前PEEC法在分析矩形PCB線圈這種特定對象時，缺少系統的剖分策略，且剖分參數的選取主要依賴經驗。同時，進一步考慮金屬渦流的PEEC建模仍有待于研究。

本文基于PEEC法，在0.5～15MHz頻率范圍內，建立了矩形螺旋PCB線圈的PEEC模型，包括銅線、介質基片、引接線，重點分析并建立了線圈下方金屬渦流的PEEC模型，并分析了各個PEEC剖分參數對計算阻抗的影響。通過分析總結給出了金屬渦流下平面矩形螺旋PCB線圈PEEC剖分參數的通用選取方法，計算分析了渦流影響下的線圈射頻磁場分布，最終實現了考慮金屬渦流下PCB線圈阻抗和射頻磁場分布的快速且準確的計算。

1 部分元等效電路理論基礎

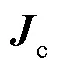
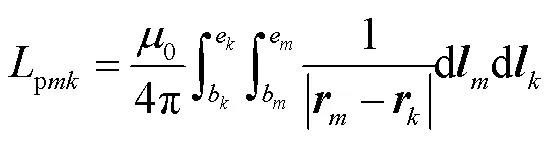
式中，rk和rm對應m和k上的坐標點。線段m的起點和終點分別為bm和em，長度為lm；線段k的起點和終點分別為bk和ek，長度為lk。

圖2 平行體單元的部分互感計算模型

PEEC建模是將電磁場問題轉化為純電路問題分析。導體剖分后，按電容單元中心為電位節點，相鄰兩電位節點之間為串聯電阻電感單元的原則，可得到圖1b所示電阻、電感與電容單元構成的等效電路。最后采用電路中的改進節點分析（Modified Nodal Analysis, MNA）法，即可求解得到導體等效阻抗。

2 平面矩形螺旋PCB線圈建模

2.1 線圈模型

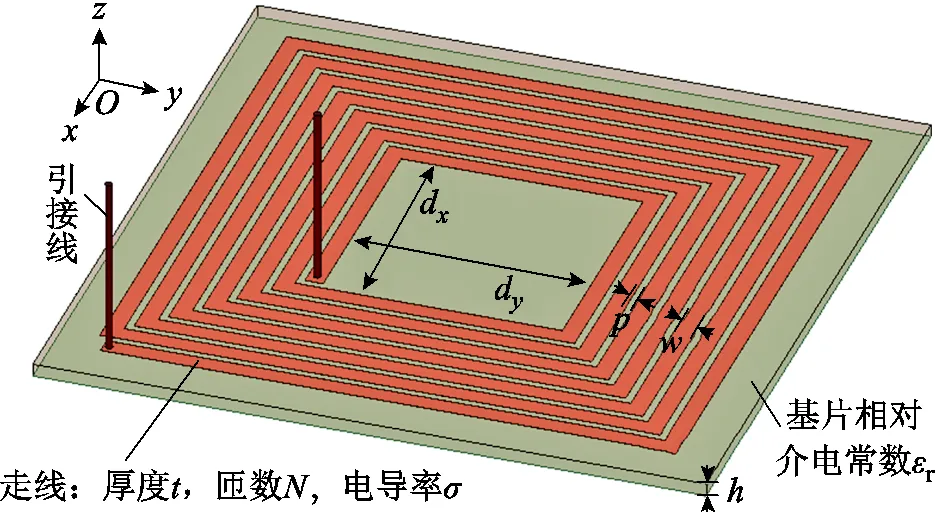
圖3 矩形螺旋PCB線圈幾何結構

2.2 部分元等效電路建模

2.2.1 直導線剖分策略

首先考慮銅線的電阻和電感效應。趨膚效應和鄰近效應使得有效電流密度集中分布在銅線表面薄層。在銅線截面剖分時，需將最外層進行細密剖分。同時，由于截面中心處的電流密度差別不大，為節約計算資源，在截面中心處采用相對粗糙的剖分。對于圖3中矩形線圈的一條邊，設長度為（電流密度方向），橫截面寬度為，厚度為（且），本文采用的銅線橫截面體剖分策略如圖4所示。

圖4 銅線橫截面的體剖分

在滿足精度的前提下，為盡量減少剖分單元數，剖分單元的寬度由表及里呈等比數列關系遞增，設等比數列的公比即趨膚因子為，且在整個寬度方向采用左右對稱剖分。銅線厚度方向可按照同樣的剖分策略。

考慮銅線表面的電容效應時，由于線寬在mm級別，而厚度只有35μm，可采用無限薄的矩形平板進行表面電容單元等效，避免對銅線側面和下底面剖分[20]。對銅線表面的電容單元剖分策略如圖5所示，首先將銅線的每一邊分割為兩段大電容單元，拐角n(=1,2,…)代表電容單元的電位節點。為體現銅線表面自由電荷分布的不均勻性，需對大電容單元進一步剖分。對每一個大電容單元，采用降低最外層單元寬度，且內層單元寬度均分的剖分方案。設內層小電容單元的寬度為in，外層小單元和內層小單元寬度之比為，且每邊剖分為個小電容單元。通過對一邊長為1m的無限薄正方形平板自電容計算得知，當=0.1，即最外層單元寬度為內層單元寬度的0.1倍，=4，即每邊分為4段小電容單元時，電容計算值即趨于穩定。

2.2.2 拐角剖分策略

平面矩形線圈拐角剖分策略如圖6所示，電流密度集中分布在矩形PCB線圈拐角的相對內側。為體現拐角電流密度分布的差異性，本文對平面矩形螺旋線圈拐角剖分采用一維非重疊剖分。

圖5 銅線表面電容單元剖分

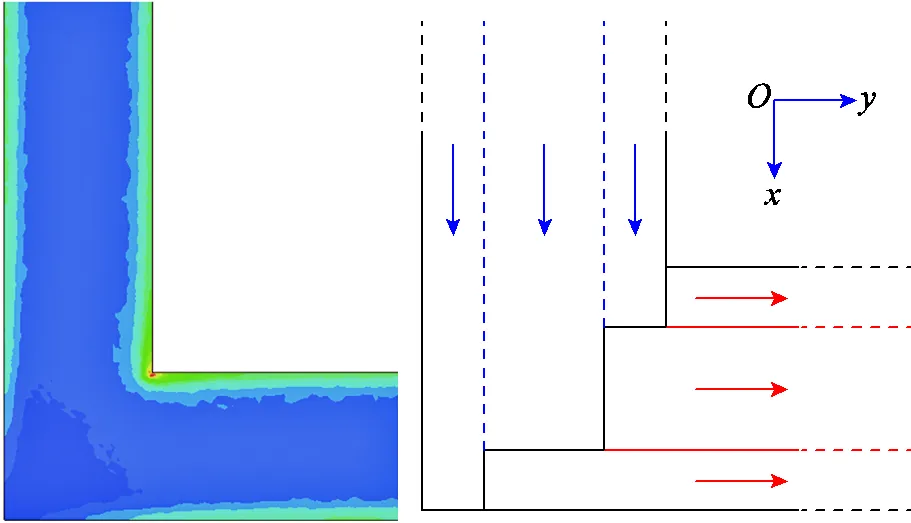
圖6 平面矩形線圈拐角剖分

2.2.3 引接線剖分策略

PCB線圈需通過引接線連接至外部電路，引接線采用橫截面為圓形的漆包線，長度為1，橫截面半徑為s。引接線剖分策略如圖7所示。

圖7 引接線剖分

引接線表面的電流密度為s，設電流密度從表面向圓心按指數規律衰減，則引接線橫截面上半徑為l處的電流密度表達式為

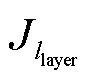
在引接線周向方向上，按照經驗公式對每一層圓環在周向方向上進行剖分[22]，為在保證計算精度的前提下減少剖分單元數，每層圓環的剖分扇形數均少于20個。每層圓環的扇形單元剖分數表達式為

式中，round()表示對四舍五入取整。

2.2.4 基片剖分

為分析全面，還需考慮銅線下方FR4基片的電容效應。介質基片建模如圖8所示。對于圖8a所示的介質基片模型，長為di，寬為di，厚度為di，在對介質基片的表面單元剖分時，只考慮上下表面的影響，將介質基片的上下兩表面視為電容單元，且定義電位節點之間的附加電容+為[23]

對比導體的等效電路，介質的等效電路需要在導體的基礎上增加附加電容，介質基片的PEEC等效電路如圖8b所示。

計算時忽略介質基片的功率損耗和極化電流的影響，即節點1和節點2只通過束縛電荷為源的表面等效部分電容關聯[19]，只考慮基片上表面和下表面的電容效應，并采用與線圈電容單元對應的映射剖分方法[16]。例如，對于基片的上表面剖分，首先將線圈正對的基片上表面分為線圈銅線正下方區域和線圈匝間空隙正下方區域，對應基片電容單元的寬度分別為銅線線寬和匝間距。對于基片表面其余區域的電容單元的寬度均設置為銅線匝間距寬度。令拐角的電位節點為電容單元的中心，介質基片的剖分策略以及基片表面與銅線表面之間的耦合電容如圖9所示。

綜合考慮線圈銅線、引接線與介質基片的PEEC模型后，單匝PCB線圈的等效電路如圖10所示。為了清楚起見，圖10中只畫出了部分電感和電容。

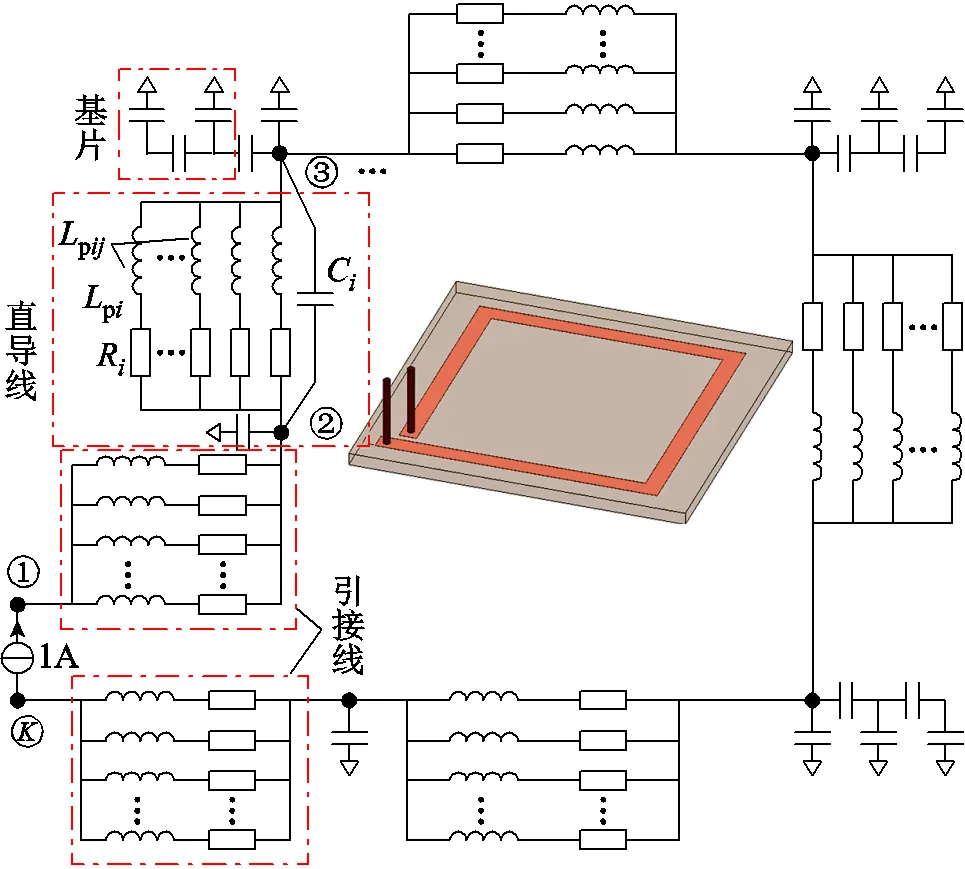
圖10 單匝線圈完整的等效電路

在圖10所示等效電路的引接線節點1和節點兩端施加單位電流，并采用式（7）的MNA方程對等效電路求解。

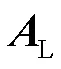
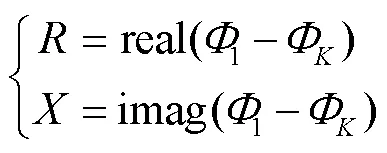
式中，real表示取實部；imag表示取虛部。

2.3 線圈剖分參數確定

本文在0.5～15MHz頻率范圍內采用PEEC法計算平面矩形螺旋PCB線圈的阻抗。為分析銅線橫截面的電流密度分布，需在電流密度大且變化劇烈的表面加密剖分，同時，為保證計算速度，在電流密度小且變化緩慢的截面中心，采用較為粗糙的剖分策略。因此，需要確定最優的PEEC剖分參數。

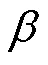
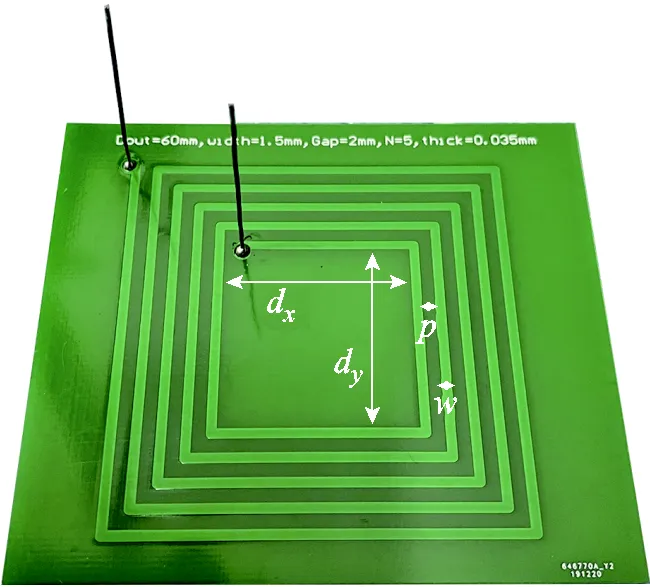
圖11 矩形線圈1

表1 矩形線圈1結構參數

Tab.1 Structural parameters of the rectangular coil 1

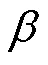
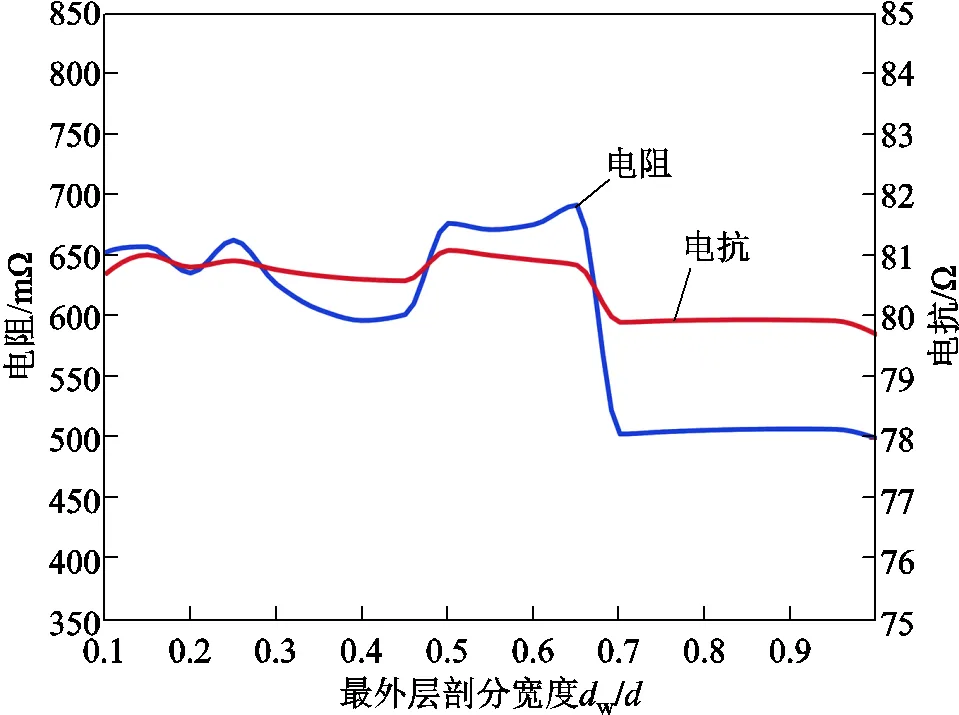
圖12 最外層剖分寬度dw對應阻抗計算值

最外層單元的剖分寬度w從0.1到變化，電抗從79.7Ω到81.1Ω，誤差范圍從4.17%到2.5%，說明PEEC剖分時，當w在趨膚深度范圍內，w的變化對電抗計算結果的影響很小。

當w＞0.3時，計算電阻值變化很大。當w在0.1～0.3之間時，電阻計算值的變化穩定，且在實測值650mΩ附近，這說明w在此范圍內時，選擇合適的趨膚因子可使電阻計算值接近實測值。本文考慮的頻率范圍為0.5～15MHz，在15MHz下，趨膚深度為17.2μm，因此，剖分計算時，將最外層剖分寬度設置為w＝4μm，即滿足所計算頻率范圍內w小于0.3倍趨膚深度的要求。

固定w＝4μm，設置趨膚因子的掃描范圍為1.1～4，得到不同下線圈1的電阻和電抗值，如圖13所示。當從4減小到1.1的過程中，計算電抗值在80～82Ω之間，且與實測電抗值的偏差始終小于4%，這是一個可接受的誤差范圍。計算電阻值受的影響較大，隨著的降低，整體呈現出減小的趨勢，且當在2.2～2.5范圍內，電阻計算值在實測值668.63mΩ附近。總體而言，計算電抗值受趨膚因子的影響較小，而計算電阻值受的影響較大。

根據圖13，在0.5～15MHz下，取w＝4μm，＝2.4，對應線圈橫截面寬度方向剖分單元數為13，最中心單元的寬度為413μm，厚度方向的剖分層數為5層。畫出PEEC法計算得到的矩形PCB線圈1的阻抗值，并與實測值對比，如圖14所示。隨著頻率的增加，計算阻抗與實測值保持了相同的變化趨勢，其中，計算電抗誤差始終小于2%，計算電阻誤差小于4%。

圖13 趨膚因子β對應阻抗計算值

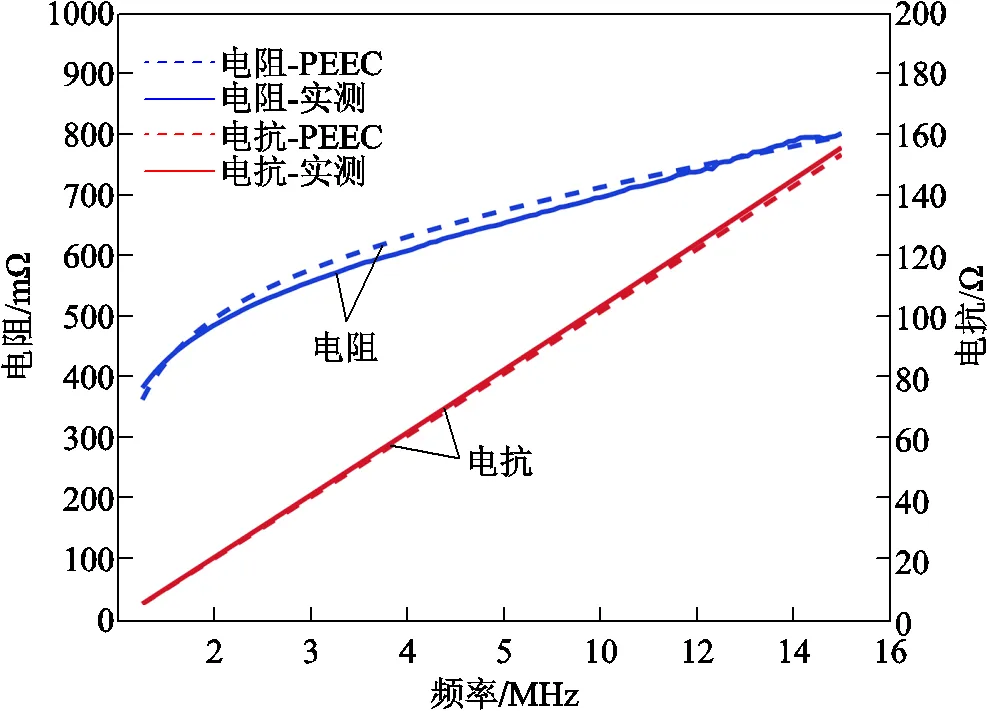
圖14 矩形線圈1的PEEC計算阻抗與實測對比（dw=4μm，β=2.4）

在采用上述剖分策略及剖分參數下，圖15顯示了PCB線圈相鄰兩直導線橫截面的相對電流密度分布。可以明顯看出，趨膚效應和鄰近效應使得有效電流密度集中分布于線圈表面。

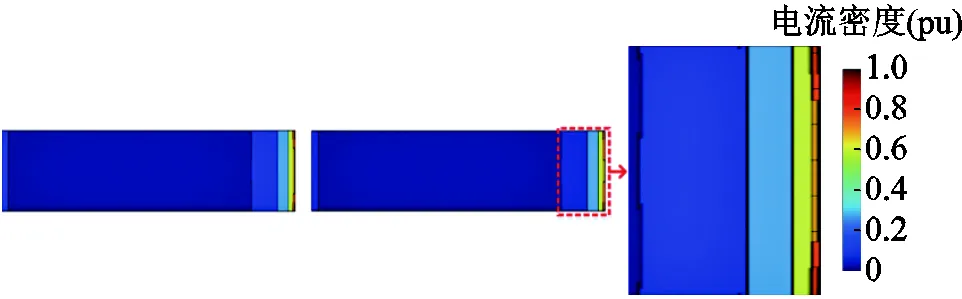
圖15 導線橫截面電流密度分布

在線圈1剖分時，w＝4μm，＝2.4，對應剖分后小長方體單元的最大寬度為413μm。由于矩形線圈1的內徑為29mm，可以得出直導線剖分后的小長方體單元的軸長與橫截面寬度構成的最小軸寬比約為70.1。在0.5～15MHz頻率范圍內，為給出平面矩形螺旋PCB線圈的一般性剖分參數選取原則，計算不同尺寸線圈的阻抗值，并與阻抗分析儀實測對比分析。結果表明，固定最外層單元寬度w＝4μm，同時為保證部分互感計算時長方體單元到線段模型的有效性，趨膚因子的選取應考慮線圈內徑，并使得剖分小長方體單元的最小軸寬比大于90即可。最終不同尺寸的矩形螺旋PCB線圈計算電阻誤差保持在20%以內，計算電抗誤差保持在2%以內。考慮到不同線圈銅線本身的電導率存在偏差，計算結果在可接受范圍內。

2.4 計算精度與效率

本文采用的PEEC法完整地考慮了矩形PCB線圈的電阻、電感和電容效應，為說明完整的PEEC法（PEEC/R+L+C）與只考慮電阻和電感的PEEC法（PEEC/R+L）在計算精度上的差異，圖16給出了阻抗分析儀實測、PEEC/R+L+C和PEEC/R+L得到的矩形PCB線圈1的阻抗對比。考慮電容效應雖對電抗影響較小，但是能明顯提高電阻值的計算精度，且隨著頻率的增加，電容效應越明顯。

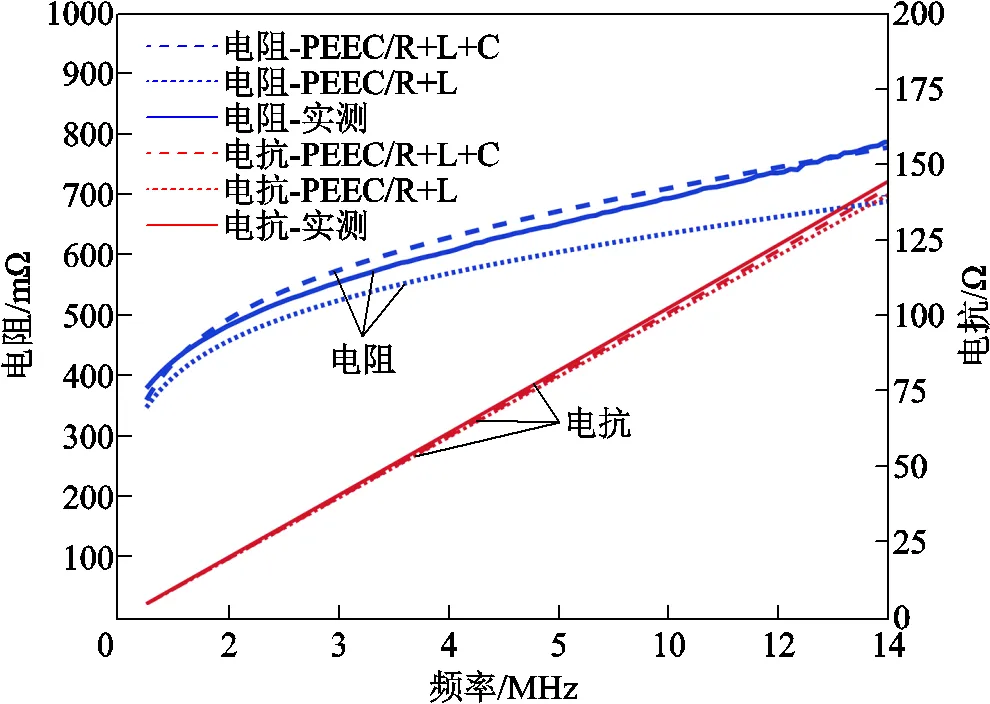
圖16 不同方式得到的矩形線圈1阻抗對比

在計算時間方面，在同一臺個人計算機上（16G內存，3.50GHz的四核AMD Ryzen 3 2200G處理器），在單一頻點下計算線圈1的阻抗，在達到相同計算精度的前提下（計算阻抗相對實測的誤差＜5%），本文PEEC/R+L+C法使用Matlab語言與基于有限元的商用軟件HFSS的計算效率對比見表2，可以看出，PEEC法極大地提高了PCB線圈的計算效率。

表2 PEEC法與有限元法計算效率對比

Tab.2 Comparison of calculation efficiency between PEEC and finite element method

3 考慮金屬渦流的線圈建模

3.1 金屬板建模

核磁測井中的射頻線圈周圍存在金屬，金屬中會產生感應渦流。由于渦流具有熱效應和去磁效應，會影響整個線圈系統的阻抗和目標區域射頻磁場的大小和分布。在考慮渦流的影響下準確計算線圈的阻抗至關重要。不失一般性，在矩形PCB線圈1正下方1cm處放置一厚度為2mm的金屬鋁板，且鋁板能完全覆蓋矩形線圈銅線的正下方區域，如圖17所示。PCB線圈與鋁板之間用載玻片隔開，鋁板參數見表3。

圖17 鋁板位于矩形線圈1下方

表3 鋁板參數

Tab.3 Parameters of aluminum plate

在8MHz下，利用阻抗分析儀實測，在鋁板存在的情況下，由于鋁板中感應出金屬渦流，渦流的熱效應導致整個線圈兩端等效電阻增加，即電阻從641mΩ增加到699mΩ；渦流的去磁效應導致線圈的磁鏈減小，從而引起電抗的降低，即線圈的電抗從83.22Ω降低到70.54Ω。線圈阻抗參數直接關系到線圈的性能，因此有必要對金屬存在下的PCB線圈阻抗變化進行分析。

由于線圈1具有平面矩形螺旋的特點，在下方金屬鋁板感應的渦流可以看作線圈中的等效電感與鋁板中的等效電感之間相互耦合而成的，因此，鋁板中感應渦流的分布應具有類似線圈中電流沿矩形螺旋流向的特點。為此，鋁板水平方向的剖分，可以看作是等寬的同軸孤立矩形渦流線圈，且鋁板中等效孤立矩形線圈的外圍長寬比與矩形PCB銅線的外圍長寬比相同，如圖18所示（圖中未畫出基片），其中每匝等效渦流線圈的寬度均為e。金屬板豎直方向則同樣按照等比數列增長的剖分方式，設置鋁板的剖分總深度為趨膚深度的倍，深度方向第一層的高度t為4μm，同時，再往下的每一層按照公比（趨膚因子）為1的等比數列增長。

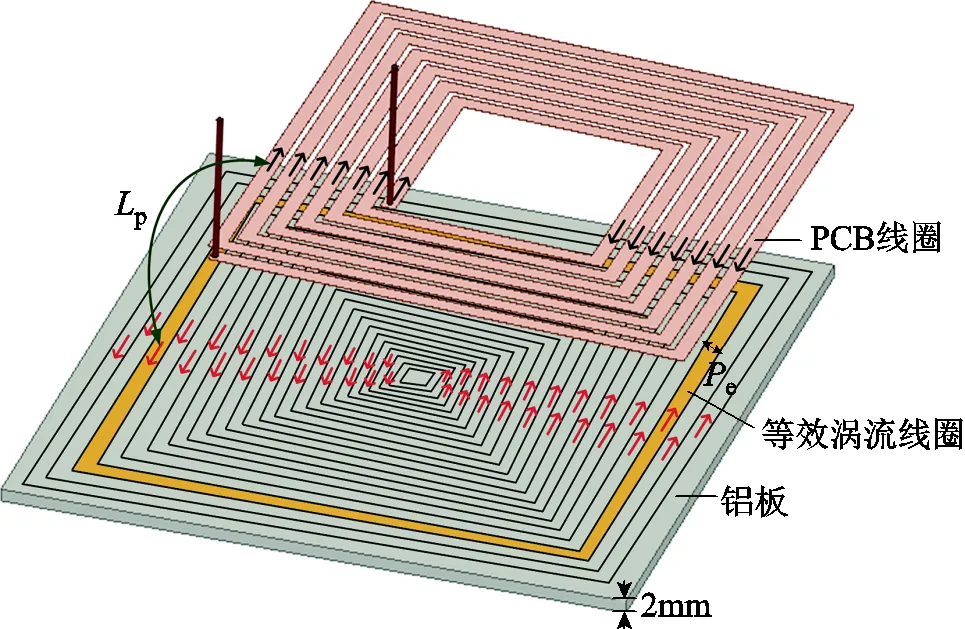
圖18 鋁板水平方向剖分

按照銅線剖分參數同樣的尋優方法，最終得到鋁板的剖分參數見表4。

表4 鋁板剖分參數

Tab.4 Meshing parameters of aluminum plate

根據表4的剖分參數，可以畫出矩形線圈1下方存在鋁板時，PEEC計算阻抗與阻抗分析儀實測阻抗隨頻率變化規律，如圖19所示，計算阻抗與實測基本吻合。由于本文主要考慮金屬鋁板與PCB線圈之間的耦合電感效應，若要使得計算結果更加精確，應更進一步考慮鋁板的表面電容效應，此時按照2.2節中基片表面電容單元的剖分方法對鋁板表面的電容單元進行剖分即可。

3.2 射頻磁場計算

當在射頻線圈兩端施加激勵時，線圈會在目標區域產生射頻磁場，通過PEEC等效，將線圈剖分為若干等效電阻和等效電感串聯的傳導電流支路，通過MNA法求得每條支路的電流幅值，再利用畢奧-薩伐爾定律即可求解得到目標區域的射頻磁場分布。

圖19 鋁板存在下線圈1阻抗計算值與實測對比

以矩形線圈1為例，當在線圈端口注入頻率為8MHz的單位電流時，對比得到了在線圈正下方有無鋁板時，線圈上方1mm處目標層面的射頻磁場分布，如圖20所示。PCB線圈下方存在鋁板時，目標層面上的射頻磁場與沒有鋁板時的射頻磁場等值線分布形狀基本一致，但是由于金屬鋁板感應渦流的去磁效應，使得目標層面射頻磁場整體強度明顯降低。在無線電能傳輸和單邊核磁測井傳感器的PCB線圈射頻磁場分析中，必須考慮金屬渦流的影響。

圖20 目標層面上射頻磁場強度歸一化分布

4 結論

本文采用PEEC法對考慮金屬渦流的PCB線圈進行電磁場求解，確定了適合0.5～15MHz頻率范圍內平面矩形螺旋PCB線圈以及金屬板的PEEC模型及剖分參數，并提出了以剖分體單元的軸長與橫截面寬度之比大于90作為趨膚因子取值上限，從而建立了不同尺寸的平面矩形螺旋PCB線圈PEEC剖分參數選取方法。本文建立的PCB線圈PEEC模型綜合考慮了電阻、電感和電容效應，實現了PCB線圈阻抗及射頻場分布的準確且快速求解。可進一步用于無線電能傳輸以及單邊核磁測井中的PCB線圈分析，同時對更高頻下的PCB線圈建模分析同樣具有借鑒意義。

[1] 卿曉東, 蘇玉剛. 電場耦合無線電能傳輸技術綜述[J]. 電工技術學報, 2021, 36(17): 3649-3663.

Qing Xiaodong, Su Yugang. An overview of electric-filed coupling wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2021, 36(17): 3649-3663.

[2] Xu Xianneng, Guo Pan, Lu Ming, et al. Optimized portable unilateral magnetic resonance sensor for assessing the aging status of silicon rubber insulators[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-11.

[3] 肖立志. 井下極端環境核磁共振科學儀器[M]. 北京: 科學出版社, 2016.

[4] 羅成鑫, 丘東元, 張波, 等. 多負載無線電能傳輸系統[J]. 電工技術學報, 2020, 35(12): 2499-2516.

Luo Chengxin, Qiu Dongyuan, Zhang Bo, et al. Wireless power transfer system for multiple loads[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2499-2516.

[5] 薛明, 楊慶新, 章鵬程, 等. 無線電能傳輸技術應用研究現狀與關鍵問題[J]. 電工技術學報, 2021, 36(8): 1547-1568.

Xue Ming, Yang Qingxin, Zhang Pengcheng, et al. Application status and key issues of wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1547-1568.

[6] 肖思宇, 馬殿光, 張漢花, 等. 耦合諧振式無線電能傳輸系統的線圈優化[J]. 電工技術學報, 2015, 30(增刊1): 221-225.

Xiao Siyu, Ma Dianguang, Zhang Hanhua, et al. The coil model of coupled magnetic resonance wireless power transmission system[J]. Transactions of China Electrotechnical Society, 2015, 30(S1): 221-225.

[7] 陳垣, 張波, 謝帆, 等. 電力電子化電力系統多時間尺度建模與算法相關性研究進展[J]. 電力系統自動化, 2021, 45(15): 172-183.

Chen Yuan, Zhang Bo, Xie Fan, et al. Research progress of interrelationship between multi-time-scale modeling and algorithm of power-electronized power system[J]. Automation of Electric Power Systems, 2021, 45(15): 172-183.

[8] 曾非同, 關向雨, 黃以政, 等. 基于多尺度多物理場的油浸式變壓器流動-傳熱數值研究[J]. 電工技術學報, 2020, 35(16): 3436-3444.

Zeng Feitong, Guan Xiangyu, Huang Yizheng, et al. Numerical study on flow-heat transfer of oil-immersed transformer based on multiple-scale and multiple-physical fields[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3436-3444.

[9] 雷銀照. 關于電磁場解析方法的一些認識[J]. 電工技術學報, 2016, 31(19): 11-25.

Lei Yinzhao. Reviews of analytical methods for electromagnetic fields[J]. Transactions of China Electrotechnical Society, 2016, 31(19): 11-25.

[10] 吳曉鵬. 車用表貼式永磁同步電機全域損耗高效計算方法研究[D]. 北京: 北京理工大學, 2016.

[11] Acero J, Hernandez P J, Burdio J M, et al. Simple resistance calculation in litz-wire planar windings for induction cooking appliances[J]. IEEE Transactions on Magnetics, 2005, 41(4): 1280-1288.

[12] 吳嘉敏. 土壤水分的磁共振測量方法基礎研究[D]. 重慶: 重慶大學, 2019.

[13] Kim D H, Park Y J. Calculation of the inductance and AC resistance of planar rectangular coils[J]. Electronics Letters, 2016, 52(15): 1321-1323.

[14] Romano D, Kova?evi?-Badstübner I, Parise M, et al. Rigorous dc solution of partial element equivalent circuit models including conductive, dielectric, and magnetic materials[J]. IEEE Transactions on Electromagnetic Compatibility, 2020, 62(3): 870-879.

[15] Baumgartner P, Bauernfeind T, Bíró O, et al. Multi-objective optimization of Yagi-Uda antenna applying enhanced firefly algorithm with adaptive cost function[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-4.

[16] Ruehli A E, Antonini G, Jiang Lijun. Circuit oriented electromagnetic modeling using the PEEC techniques[M]. Hoboken: Wiley, 2017.

[17] (蘇)卡蘭塔羅夫, (蘇)采依特林. 電感計算手冊[M].陳湯銘, 劉保安, 羅應立, 等譯. 北京: 機械工業出版社, 1992.

[18] 高飛, 陳維江, 李國富, 等. 基于完備集合思想的多導體部分電感計算方法[J]. 中國電機工程學報, 2011, 31(34): 127-134.

Gao Fei, Chen Weijiang, Li Guofu, et al. Calculating method of multi-conductor partial inductance based on complete set[J]. Proceedings of the CSEE, 2011, 31(34): 127-134.

[19] 鐘玉林, 咸哲龍, 孫旭東, 等. 計及部分電容的接地回路高頻電路模型[J]. 中國電機工程學報, 2005, 25(17): 37-41, 149.

Zhong Yulin, Xian Zhelong, Sun Xudong, et al. HF circuit model of conducted EMI of ground net based on PEEC[J]. Proceedings of the CSEE, 2005, 25(17): 37-41, 149.

[20] Scholz P, Ackermann W, Weiland T. PEEC antenna modeling of rectangular spiral inductors for RFID systems[J]. COMPEL-the International journal for computation and mathematics in electrical and electronic engineering, 2010, 29(6): 1453-1463.

[21] Lyu Jiahua, Chen Hongcai, Zhang Yang, et al. Fast simulation of Litz wire using multilevel PEEC method[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 12612-12616.

[22] Chen Hongcai, Du Yaping. Proximity effect modelling for cables of finite length using the hybrid partial element equivalent circuit and artificial neural network method[J]. IET Generation, Transmission & Distribution, 2018, 12(16): 3876-3882.

[23] He Junping, Tao Sili, Wu Huazhao. A PEEC-based concise broadband physical circuit modeling method with parameter extraction for PCB inductive components[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10852-10862.

Research on the Partial Element Equivalent Circuit of Radio Frequency Coil on the Printed Circuit Board

Xu Xianneng Xu Zheng

（School of Electrical Engineering Chongqing University Chongqing 400044 China）

PCB coils have the features of excellent performance, less space and easy manufacture artwork, and they are often used in fields of wireless power transmission and unilateral nuclear magnetic logging. In order to analyze the performance of PCB coil, it is necessary to calculate AC resistance, inductance and radio frequency magnetic field distribution. Due to the large span of copper wire thickness and outer dimensions, the calculation speed and accuracy of conventional finite element software and analytical methods cannot meet requirements, particularly when considering the metal eddy currents. In the frequency range of 0.5～15MHz, this paper adopted the partial element equivalent circuit (PEEC) method to calculate the impedance and radio frequency magnetic field distribution of PCB coil (copper thickness of 35μm) under metal eddy current. The PEEC model of the planar rectangular spiral PCB coil was established, the method for selecting the PEEC meshing parameters was summarized by making a comparison between calculation and the measurement results and the magnetic field distribution of the coil under PEEC model was analyzed. Finally, the accurate and fast calculation of the impedance and the radio frequency magnetic field of PCB coil under metal eddy current was realized. The work in this paper can provide references for PCB coil analysis in the fields of wireless power transmission and unilateral nuclear magnetic logging.

Partial element equivalent circuit, printed circuit board (PCB) coil, multiscale, AC resistance, eddy current

10.19595/j.cnki.1000-6753.tces.211013

TM13；TH89

國家自然科學基金資助項目（52077023）。

2021-07-04

2021-10-18

徐顯能 男，1994年生，博士研究生，研究方向為電磁場數值計算。E-mail：xuxianneng@cqu.edu.cn

徐 征 男，1980年生，博士，教授，研究方向為電磁場數值計算。E-mail：xuzheng@cqu.edu.cn（通信作者）

（編輯 李冰）