輸電線路單導線覆冰和扭轉的相互影響機制分析

韓興波 吳海濤 郭思華 蔣興良 王鈺潔

輸電線路單導線覆冰和扭轉的相互影響機制分析

韓興波1吳海濤2郭思華2蔣興良3王鈺潔4

（1. 交通工程應用機器人重慶市工程試驗室（重慶交通大學） 重慶 400074 2. 國網重慶市電力公司電力科學研究院 重慶 401123 3. 輸配電裝備及系統安全與新技術國家重點試驗室（重慶大學） 重慶 400044 4. 重慶交通大學機電與車輛工程學院 重慶 400074）

覆冰威脅輸電線路的安全穩定運行，準確地預測導線覆冰增長是輸電線路防冰減災工作的基礎。導線覆冰增長一般都伴隨著導線的扭轉過程，扭轉和覆冰增長的相互影響使得導線各個位置覆冰速率不同、冰形更為多樣復雜。為提高導線覆冰數值計算的準確度，該文從流體力學和導線扭轉基本力學出發，綜合考慮導線各處扭轉角度的差異和扭轉冰形對空氣中過冷卻水滴擾流特性的影響，建立了導線覆冰扭轉動態數值計算模型。通過仿真計算重點分析了三種不同型號的導線不同位置覆冰后扭轉角度的變化規律，以及導線扭轉對覆冰增長的影響特性。結果表明：覆冰后，導線扭轉角度從兩端向中心逐漸增大；相對于未扭轉，導線扭轉條件下的水滴碰撞范圍更大，覆冰速率更快；導線端部和中心位置覆冰形態差異較大，導線端部扭轉角度較小，覆冰趨于翼形；導線中部扭轉角度大，覆冰趨于圓筒形，風速和空氣中水滴中值體積直徑較大時，大直徑導線在扭轉條件下的覆冰增長速率更快。

導線 覆冰 扭轉

0 引言

我國領土遼闊，地形地貌、地質條件多種多樣，氣象環境復雜多變。隨著超/特高壓電網的建設和發展，輸電走廊覆蓋區域越來越廣，輸電線路不可避免地經過一些地形復雜、氣候高寒的重覆冰區域[1]。從1954年開始有記錄電力線路覆冰災害事故以來，我國各類輸電線路冰害事故達上千起[2-3]。自2008年我國南方電網大面積覆冰災害以來，大量人力、物力、財力的投入并沒有完全解決輸電線路絕緣子覆冰問題，絕緣子覆冰造成的輸電線路停運仍時有發生[4-6]。

導線的影響因素眾多，R. Lenhard[7]于1955年提出基于降水量的導線覆冰量計算模型，其認為導線覆冰增長主要由降水量決定。K. Jone等[8]認為導線覆冰與降水率、風速和液態水含量等環境因素相關，導線表面等值覆冰厚度可根據環境條件用經驗公式計算。L. Makkonen等[9]總結了導線覆冰涉及三個基本物理過程，即水滴在導線表面的碰撞、捕獲和凍結過程。此外，提出了以水滴碰撞、捕獲和凍結系數計算導線覆冰增長的動態過程（三參數模型）。Fu Ping等[10]利用數值模擬方法，仿真計算了導線水滴局部碰撞系數分布，提高了導線覆冰數值模擬的準確度。為了減少水滴碰撞系數的仿真計算量，郭昊等[11]提出了導線覆冰的工程估算方法，但僅可在覆冰初始階段采用。

在后續研究中，三參數模型被廣泛采用，但其所需覆冰環境參數，尤其是空氣中液態水含量和過冷卻水滴的中值體積直徑卻不易獲得。陳凌[12]、蔣興良[13]、韓興波[14]等通過制作旋轉多導體裝置實現了覆冰環境參數的實時采集。在此基礎上，Zhang Jian[15-16]、蔣興良[17]、梁曦東[18]等通過計算流體動力學（Computational Fluid Dynamics, CFD）或邊界元法建立了導線覆冰增長的實時動態模型，實現了對覆冰形態、覆冰量的動態模擬。

總結上述導線覆冰數值計算模型，不難發現：①導線覆冰是環境和結構的相互作用結果，覆冰增長類型、速率、形態主要決定于環境參數，但導線本身的結構也有一定影響；②導線覆冰增長是個動態過程，覆冰形態變化同樣也會影響覆冰的后續發展情況。尤其導線本身的狀態也會影響覆冰發展過程。導線在覆冰后通常發生扭轉、翻轉現象[19-20]，導線的扭轉一方面會損傷線路金具，另一方面也會反作用于覆冰過程。導線在扭轉過程中，覆冰積累的位置實時改變，覆冰速率、冰形隨之改變，而導線各個位置扭轉角度的差異也會使得覆冰增長過程存在差異[21-22]。如胡琴等[23]通過現場觀察發現：自然覆冰條件下，懸垂單導線和分裂導線覆冰形態差異明顯，這是由導線扭轉剛度所決定的，相同覆冰條件下，單導線覆冰后扭轉角度相對分裂導線更大。而以往的導線覆冰模型通常并未考慮扭轉和覆冰增長的相互作用，導致導線覆冰模型預測準確度的降低。李清等[24]和樊社新等[25]對覆冰導線的扭轉剛度開展了試驗研究及仿真計算，研究發現，導線的扭轉剛度隨覆冰厚度的增加而增大，而分裂導線不同位置的扭轉剛度也不相同，扭轉剛度在近跨端處隨初始張力增大而增大，隨檔距增大而減小，且均在近跨端處較為敏感而近跨中處較不敏感。解健等[26]在研究分裂導線覆冰扭轉中發現，偏心覆冰及上升氣流等因素易導致大檔距多分裂導線劇烈扭轉，嚴重時會引發翻轉扭絞故障，扭轉角度和轉矩的關系可通過有限元仿真獲得。P. L. I. Skelton和G. Poots等[27]針對導線覆雪扭轉現象開展了模型化研究，其研究發現，雪的密度較小，但是在暴風雪條件下，雪的累積速度較快，導線受力后的扭轉角度可達120°～130°（導線中部）。

本文以單導線為對象，研究導線覆冰過程和扭轉過程的相互影響。首先從試驗觀測結果入手，分析導線覆冰不均勻性和覆冰冰形在扭轉條件下的變化情況；其次，基于流體力學和基本力學原理建立導線覆冰扭轉數值計算模型，通過仿真模擬獲得導線扭轉條件下導線覆冰冰形、增長速率的變化規律；最后，結合試驗觀測結果，對比分析導線覆冰和扭轉的相互作用機理。本文研究內容可為導線防覆冰扭轉工程運用提供技術參考。

1 導線自然覆冰扭轉觀測

本文在雪峰山對導線覆冰扭轉現象展開觀測。雪峰山海拔1 400m，年平均降水量為1 500mm，最大風速超過35m/s，最低氣溫-15℃。特殊的微地形微氣象特征導致雪峰山年覆冰持續時間最長達50天，最大覆冰厚度可至500mm。

導線未扭轉時的覆冰形態變化如圖1所示，覆冰主要在導線迎風側累積，形成尖銳的翼型結構覆冰。導線扭轉時的覆冰形態變化如圖2所示，導線受到覆冰扭轉力矩的作用向下扭轉，而覆冰未停止，導線背風側向迎風側偏移，覆冰面積擴大，同時，原迎風側的覆冰繼續增加，覆冰形態變得不規則。

圖1 導線未扭轉時的覆冰形態變化

圖2 導線扭轉時的覆冰形態變化

2 導線覆冰扭轉計算模型

空氣中的過冷卻水滴隨氣流運動，當遭遇導線時，水滴在慣性作用下碰撞到導線并凍結為覆冰。根據Makkonen導線覆冰模型的基本思想，要獲得水滴在導線表面的水滴碰撞效率，需求解導線外部氣流場。簡化到二維平面后，氣流運動可被看作低速的不可壓縮的粘性流動，其動量方程和連續性方程可表示為Navier-Stokes方程（N-S方程），即

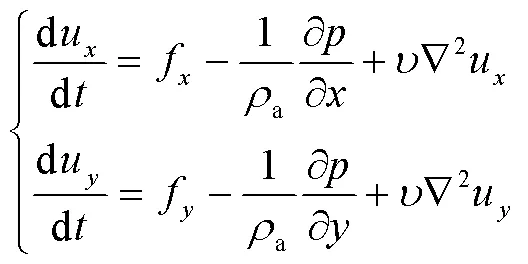
式中，f、f、f為質量力沿著各個坐標方向分力，N；u、u、u為氣流在各個坐標軸上的速度，m/s；a為氣流密度，kg/m3；為壓強，Pa；對應a-1·?/?為氣流受到的壓差力；第三項為黏性力，為空氣運動黏度，m2/s。水滴運動可看作離散項，其運動方程可表示為

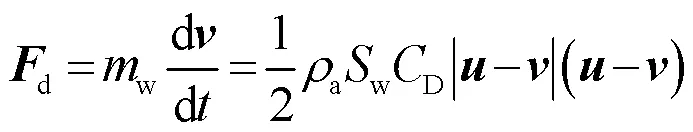
式中，d為水滴受到氣流的拽力，N；w為水滴質量，kg；w為水滴最大橫截面積，m2；、分別為氣流和水滴的二維速度向量，m/s；D為空氣阻尼系數。直接求解N-S方程時計算過程復雜，計算效率較低，因此本文采用邊界元法[28]求解導線外部氣流場，在氣流場基礎上利用式（3）跟蹤計算水滴運動軌跡和碰撞坐標點，導線表面局部碰撞系數1可參考陳凌經驗公式[12]，局部凍結系數3可根據熱平衡方程[9]計算，若不考慮水滴碰撞導線后的反彈，則導線表面覆冰增長速率為

式中，為風速，m/s；為空氣中液態水含量，kg/m3；為導線直徑，m；為導線長度，m。

導線覆冰扭轉示意圖如圖3所示。覆冰開始后，對于單導線而言，導線在覆冰偏心轉矩的作用下繞中心軸扭轉。

圖3 導線覆冰扭轉示意圖

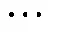
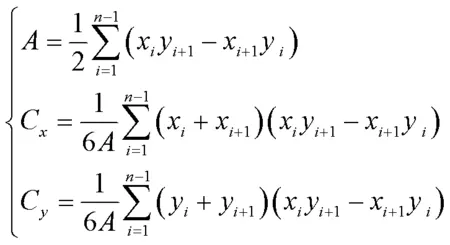
若已知導線的剪切模量為，導線截面極慣性矩是，導線覆冰后的扭轉角度為，則有[23,29]

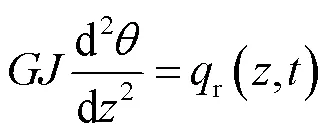
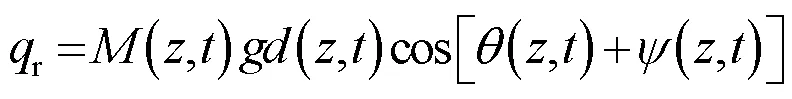
根據式（6）和式（7）可得

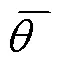
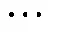
其中

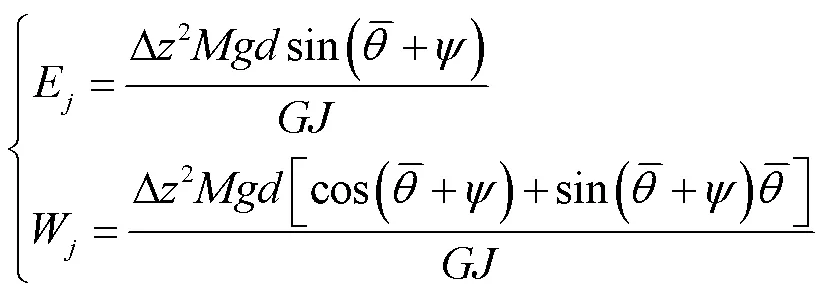
由此，若導線上各點的覆冰質量已知，則根據式（12）可得到在該覆冰量下導線各點的扭轉角度。本文將導線覆冰數值模擬和導線覆冰后扭轉計算進行耦合，通過迭代計算實現導線覆冰增長和扭轉的動態模擬。

本文建立的導線覆冰扭轉模型的計算流程如圖4所示。為減少計算量，以個間隔點Q將導線分為-1個單元，每個單元內導線覆冰量和覆冰扭轉角度相同。

首先，輸入環境參數溫度、空氣中液態水含量、風速、水滴中值體積直徑（Median Volume Diameter, MVD）等，針對導線各個分割點計算外部氣流場分布，進而對水滴軌跡進行跟蹤，獲得未覆冰或已覆冰條件下導線各處的水滴局部碰撞系數1。通過求解水滴凍結熱平衡方程獲得碰撞水滴的凍結比例，即水滴凍結系數3。由此，根據式（4）構造導線各點覆冰冰形，得到覆冰質量。其次，根據覆冰結果計算導線各點在當前覆冰量下的扭轉角度θ，并以扭轉角度更正覆冰位置。最后，通過反復迭代即可獲得導線覆冰扭轉的動態變化過程。

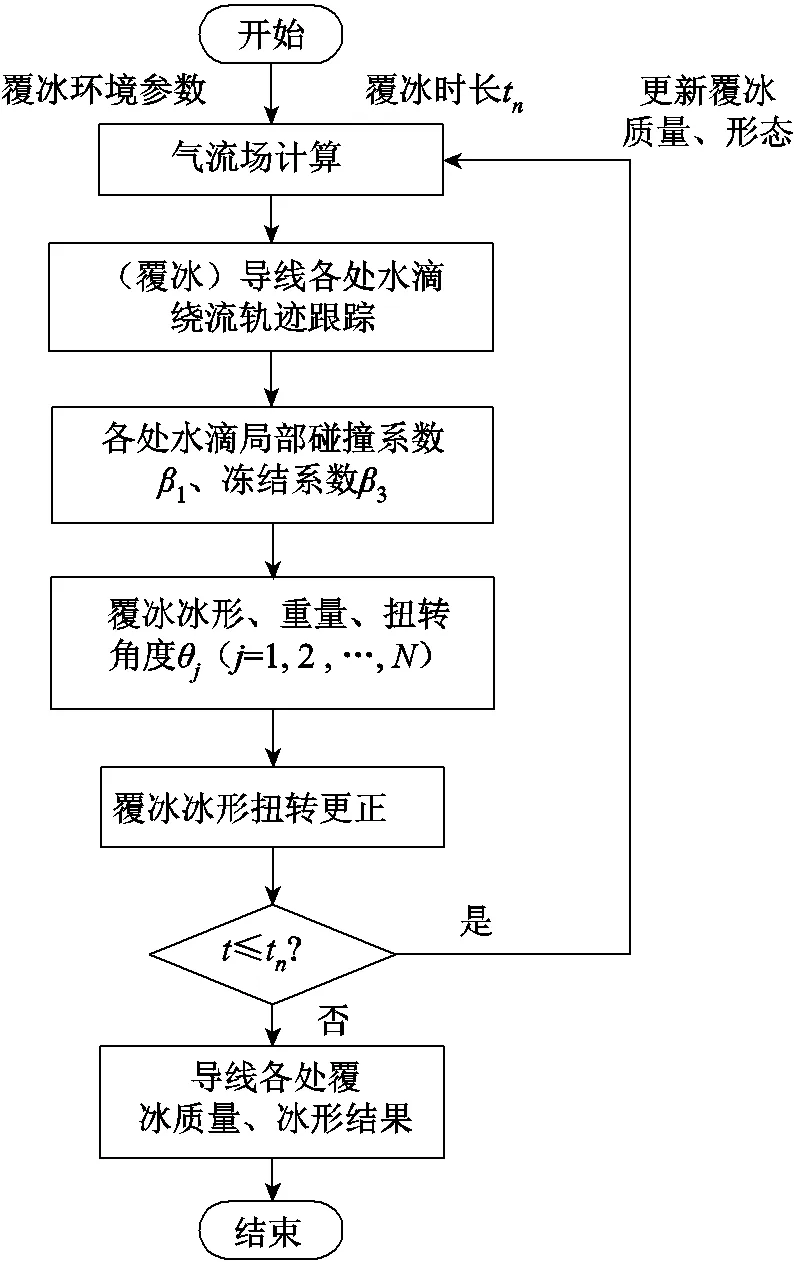
圖4 導線覆冰扭轉數值模型計算流程

3 導線覆冰扭轉特性

3.1 不同導線的覆冰扭轉特性

導線覆冰受到多種因素的影響。本文考慮導線兩端為完全固定點，忽略線夾安裝及松動等因素的作用。其次，在線路結構中，導線的懸掛點高度差為主要影響因素，導線覆冰后，因覆冰重量分解到垂直于導線的分量不同，兩端的扭轉角度也會有差異，為簡化問題，導線兩端連接點被視作水平。設定迭代時間步長為15min，導線扭轉是一個連續的過程。單導線的扭轉剛度為

式中，為導線的擰繞系數，=0.12；1和2分別為鋼芯和鋁鉸層的彈性模量，1=81GPa，2=28GPa；1和2分別為鋼芯和鋁鉸層的極慣性矩。

對比導線扭轉和未扭轉條件下的覆冰增長特性，如圖5所示。若導線不扭轉，覆冰主要在迎風側累積，在設定條件下，覆冰形態逐漸變得尖銳，形成翼型結構冰形，這和試驗觀測結果相吻合。在導線扭轉條件下，導線表面的主要覆冰區域實時改變，背風側向迎風側偏移，覆冰均勻性相對更好，圓筒形的覆冰形態也和試驗觀測結果類似。以LGJ-630/45、LGJ-300/25、LGJ-150/35三種單導線為例，導線主要參數見表1，設定導線長度為400m，將導線結構參數代入本文計算模型。設定迭代時間步長及環境參數，計算單導線覆冰和扭轉的動態變化情況，在覆冰75min后，得到結果如圖6～圖8所示。

圖5 導線未扭轉及扭轉條件下的覆冰增長對比

表1 典型單導線主要參數

Tab.1 Parameters of typical conductor

圖6和圖7為三種導線在75min后0～200m長度內的扭轉角度和覆冰形態。由圖6和圖7可以看出：

（1）三種導線的覆冰扭轉角度均從靠近桿塔位置（= 0m）向導線中間位置（=200m）逐漸增大，增長速率先快后慢，導線中心位置扭轉角度最大。

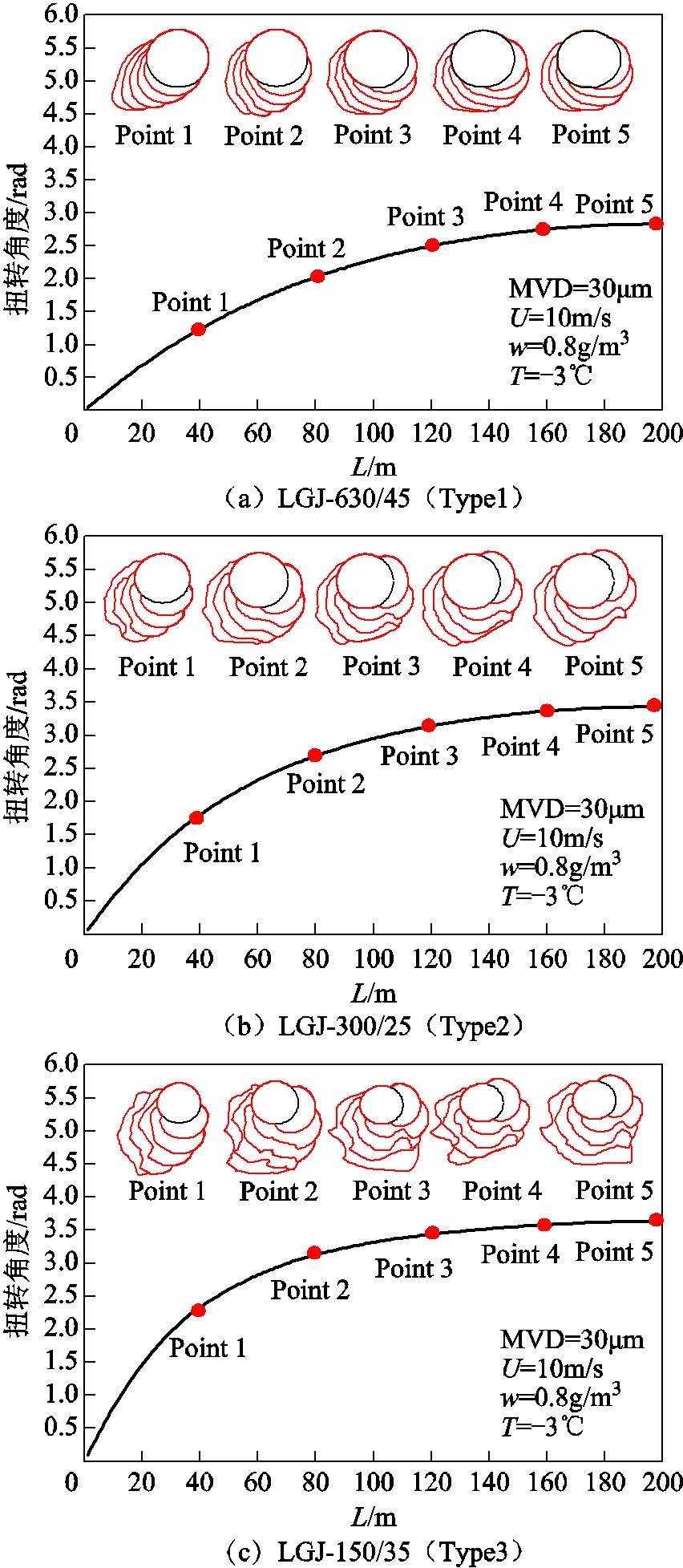
圖6 三種導線最終覆冰扭轉角度及形態（t=75min）

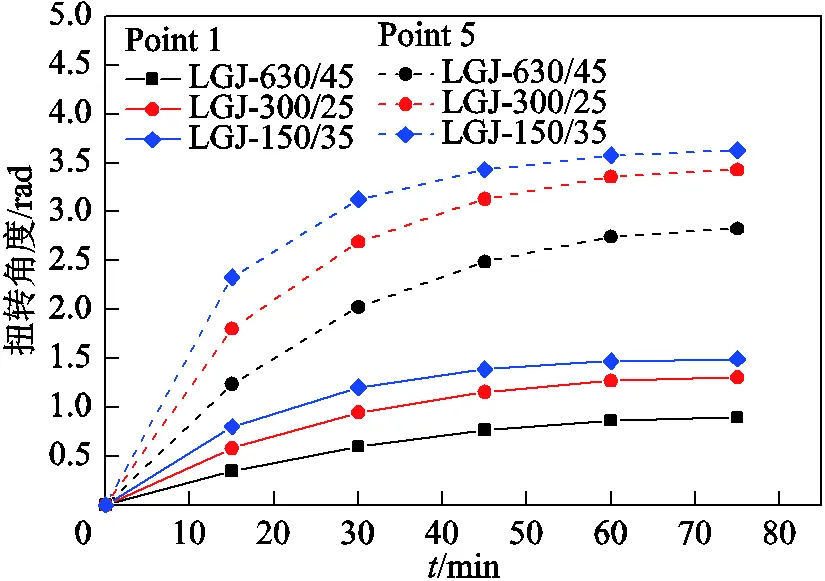
圖7 三種導線覆冰扭轉角度（取兩個點）

（2）對比導線扭轉角度，Type 3＞Type 2＞Type 1，這是因為導線Type 1～Type 3直徑依次減小，扭轉剛度也依次減小，覆冰后導線扭轉更加容易。如圖7所示，在Point 5 和Point 1處，Type 2、Type 3導線扭轉角度均大于Type1。

圖8 三種導線覆冰質量（取兩個點）

（3）橫向對比同種導線不同位置覆冰形態，靠近導線中心位置處（Point 5）的覆冰更為均勻，靠近桿塔（Point 1）處則趨于翼型結構覆冰。縱向對比不同導線同一位置，相對導線Type 1，直徑較小的Type 2、Type 3 導線表面的覆冰覆蓋面積更大，覆冰更趨于圓筒形結構，這是因為直徑較小的導線覆冰扭轉的發展速率更快。

3.2 扭轉對導線覆冰增長的影響

上面討論了導線覆冰后，不同直徑、扭轉剛度和導線不同位置的扭轉特性。而導線扭轉本身也會反作用于覆冰增長過程，除影響導線覆冰形態，還會影響導線覆冰增長速率。如圖8所示，取三種導線Point 1 和Point 5 的覆冰質量做對比，可以發現，對于同一種導線，在覆冰初期（＜30min），由于導線扭轉角度較小，導線靠近桿塔位置和導線中心位置的覆冰增長過程相同，Point 1 和Point 5 的覆冰速率基本一致。在覆冰后期（＞30min），導線扭轉角度逐漸增大，且不同位置的扭轉角度不同，導線中部Point 5的扭轉角度逐漸超過導線靠近桿塔處的Point 1，Point 5 由于扭轉角度較大，覆冰速率也逐漸超過Point 1。究其原因，相對于不扭轉的條件下，導線表面的水滴碰撞點如圖9所示，覆冰導線在扭轉后的水滴碰撞面積會更大，水滴捕獲量增加，導致了覆冰速率的增大。

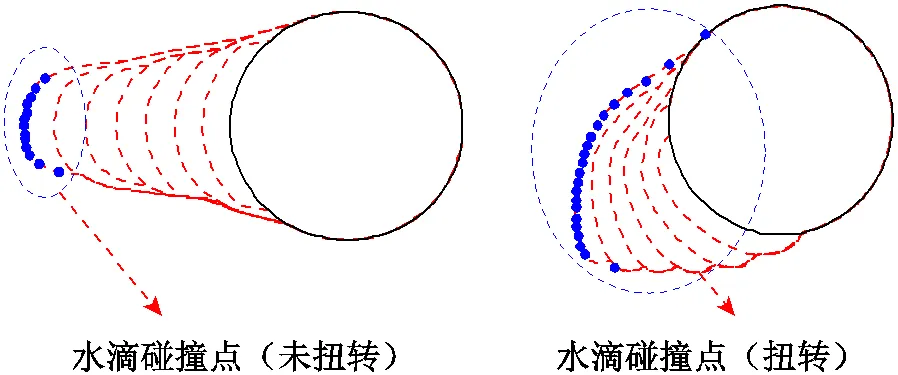
圖9 導線表面的水滴碰撞點

其次，對比三種不同的導線的覆冰速率，對于Point 1和Point 5，都存在LGJ-630/45＞LGJ-300/25＞LGJ-150/35，其原因如下，根據式（4），導線覆冰速率由導線直徑、1、3、和等因素決定，在風速和MVD較大時，大直徑導線和小直徑導線的水滴碰撞系數1、3差別較小，導線覆冰速率和導線直徑成正相關。

4 結論

1）導線覆冰過程在受到環境參數影響的同時也受到覆冰扭轉的影響，扭轉狀態下的導線的覆冰形態、速率等均有別于未扭轉狀態下的導線。

2）基于流體力學和基本力學，考慮了導線扭轉對導線覆冰增長的相互影響作用，建立了導線覆冰扭轉數值計算模型，為導線扭轉狀態下復雜冰形的模擬奠定了基礎。

3）仿真結果顯示，相對于未扭轉狀態，導線扭轉條件下的水滴碰撞范圍更大，覆冰速率更快。相對于導線靠近桿塔位置，導線中心位置的覆冰扭轉發展速率更快，覆冰易發展為環形狀，導線端部則趨于翼型覆冰。

4）不同型號的導線覆冰扭轉特性不同，導線扭轉剛度越大，直徑越大，導線覆冰后扭轉發展越慢。在風速和MVD較大時，較大直徑的導線在扭轉條件下的覆冰速率更快，但該模擬結果仍待進一步的現場試驗的驗證。

[1] 蔣興良, 鄒佳玉, 韓興波, 等. 自然環境絕緣子長串覆冰直流閃絡特性[J]. 電工技術學報, 2020, 35(12): 2662-2671.

Jiang Xingliang, Zou Jiayu, Han Xingbo, et al. DC flashover characteristics of natural environment insulators covered with ice[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2662-2671.

[2] 孫才新. 重視和加強防止復雜氣候環境及輸變電設備故障導致電網大面積事故的安全技術研究[J]. 中國電力, 2004, 37(6): 5-12.

Sun Caixin. Strengthen research of safety technology to prevent large-scale accidents caused by complex climate environment and power transmission and transformation equipment failure[J]. Electric Power Construction, 2004, 37(6): 5-12.

[3] 翁秉鈞, 楊耿杰, 高偉, 等. 一種基于改進k均值聚類的輸電線路覆冰狀態偵測方法[J]. 電氣技術, 2021, 22(5): 43-49.

Weng Bingjun, Yang Gengjie, Gao Wei, et al. A detection method for transmission line icing via improved k-means clustering[J]. Electrical Engineering, 2021, 22(5): 43-49.

[4] 胡毅. 電網大面積冰災分析及對策探討[J]. 高電壓技術, 2008, 34(2): 215-219.

Hu Yi. Analysis and countermeasures discussion for large area icing accident on power grid[J]. High Voltage Engineering, 2008, 34(2): 215-219.

[5] 舒立春, 劉延慶, 蔣興良, 等. 盤型懸式絕緣子串自然覆冰直流放電發展路徑特點及影響因素分析[J]. 電工技術學報, 2021, 36(8): 1726-1733.

Shu Lichun, Liu Yanqing, Jiang Xingliang, et al. Analysis on the dc discharge path of ice-covered disc type suspension insulators under natural conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1726-1733.

[6] 黃亞飛, 蔣興良, 任曉東, 等. 采用渦流自熱環防止輸電線路冰雪災害的方法研究[J]. 電工技術學報, 2021, 36(10): 2169-2177.

Huang Yafei, Jiang Xingliang, Ren Xiaodong, et al. Study on preventing icing disasters of transmission lines by use of eddy self-heating ring[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2169-2177.

[7] Lenhard R. An indirect method for estimating the weight of glaze on wires[J]. Bulletin of the American Meteorological Society, 1955, 36(1): 1-5.

[8] Jones K. A simple model for freezing rain ice loads[J]. Atmospheric Research, 1998, 46(1-2): 87-97.

[9] Makkonen L. Modeling of ice accretion on wires[J]. Journal of Applied Meteorology, 1984, 23(6): 929-939.

[10] Fu Ping, Farzaneh M, Bouchard G. Two-dimensional modelling of the ice accretion process on transmission line wires and conductors[J]. Cold Regions Science and Technology, 2006, 46(2): 132-146.

[11] 郭昊, 劉沛清, 屈秋林, 等. 輸電線霧凇覆冰的工程估算方法[J]. 高電壓技術, 2011, 37(4): 1041-1049.

Guo Hao, Liu Peiqing, Qu Qiulin, et al. Estimation engineering method of rime accretion process on transmission lines[J]. High Voltage Engineering. 2011, 37(4): 1041-1049.

[12] 陳凌, 蔣興良, 胡琴, 等. 自然條件下基于旋轉多圓柱體覆冰厚度的絕緣子覆冰質量估算[J]. 高電壓技術, 2011, 37(6): 1371-1376.

Chen Ling, Jiang Xingliang, Hu Qin, et al. Evaluation of ice mass on insulator under natural icing condition based on the ice thickness accumulated on rotating multi-cylinder[J]. High Voltage Engineering, 2011, 37(6): 1371-1376.

[13] 蔣興良, 申強, 舒立春, 等. 利用旋轉多圓柱導體覆冰質量預測濕增長過程覆冰參數[J]. 高電壓技術, 2009, 35(12): 3071-3076.

Jiang Xingliang, Shen Qiang, Shu Lichun, et al. Prediction of wet growth icing parameters by icing quantity of rotating multi-cylindrical conductors[J]. High Voltage Engineering, 2009, 35(12): 3071-3076.

[14] 韓興波, 蔣興良, 畢聰來, 等. 基于分散型旋轉圓導體的覆冰參數預測[J]. 電工技術學報, 2019, 34(5): 1096-1105.

Han Xingbo, Jiang Xingliang, Bi Conglai, et al. Prediction of icing environment parameters based on decentralized rotating conductors[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1096-1105.

[15] Qing He, Jian Zhang, Mengyan Deng, et al. Rime icing on bundled conductors[J]. Cold Regions Science and Technology, 2019, 158: 230-236.

[16] Zhang Jian, Makkonen L, He Qing. A 2d numerical study on the effect of conductor shape on icing collision efficiency[J]. Cold Regions Science and Technology, 2017, 143: 52-58.

[17] 蔣興良, 姜方義, 汪泉霖, 等. 基于最優時間步長模型的輸電導線霧凇覆冰預測[J]. 電工技術學報, 2018, 33(18): 4408-4418.

Jiang Xingliang, Jiang Fangyi, Wang Quanlin, et al. Prediction of rime accretion on transmission line based on optimal time step model[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 4408-4418.

[18] 梁曦東, 李雨佳, 張軼博, 等. 輸電導線的覆冰時變仿真模型[J]. 高電壓技術, 2014, 40(2): 336-343.

Liang Xidong, Li Yujia, Zhang Yibo, et al. Time-dependent simulation model of ice accretion on transmission line[J]. High Voltage Engineering, 2014, 40(2): 336-343.

[19] Keutgen R, Lilien J, Yukino T. Transmission line torsional stiffness confrontation of field-tests line and finite element simulations[J]. IEEE Transactions on Power Delivery, 1999, 14(2): 567-578.

[20] Wang J, Lilien J. A new theory for torsional stiffness of multi-span bundle overhead transmission lines[J]. IEEE Transactions on Power Delivery, 1998, 13(4): 1405-1411.

[21] 傅觀君, 王黎明, 關志成, 等. 架空輸電線路分裂導線扭轉剛度及舞動機理分析[J]. 高電壓技術, 2013, 39(5): 1273-1280.

Fu Guanjun, Wang Liming, Guan Zhicheng, et al. Torsional stiffness and galloping mechanism analysis on bundle conductors for overhead transmission lines[J]. High Voltage Engineering, 2013, 39(5): 1273-1280.

[22] 朱寬軍, 劉彬. 架空輸電線路分裂導線扭轉剛度的計算[J]. 電網技術, 2010, 34(3): 210-214.

Zhu Kuanjun, Liu Bin. Calculation of torsional stiffness of bundle conductors in overhead transmission lines[J]. Power System Technology, 2010, 34(3): 210-214.

[23] 胡琴, 于洪杰, 徐勛建, 等. 分裂導線覆冰扭轉特性分析及等值覆冰厚度計算[J]. 電網技術, 2016, 40(11): 3615-3620.

Hu Qin, Yu Hongjie, Xu Xunjian, et al. Study on torsion characteristic and equivalent ice thickness of bundle conductors[J]. Power System Technology, 2016, 40(11): 3615-3620.

[24] 李清, 馬倫, 解健, 等. 大檔距多分裂輸電導線扭轉剛度計算分析[J]. 高壓電器, 2020, 56(2): 158-162.

Li Qing, Ma Lun, Xie Jian, et al. Calculation and analysis on torsional stiffness of large?span multi?conductor bundle[J]. High Voltage Apparatus, 2020, 56(2): 158-162.

[25] 樊社新, 何國金, 廖小平, 等. 結冰導線扭轉剛度試驗[J]. 中國電力, 2005, 38(10): 45-47.

Fan Shexin, He Guojin, Liao Xiaoping, et al. Tests on tensional stiffhess of iced conductor[J]. Electric Power, 2005, 38(10): 45-47.

[26] 解健. 大檔距多分裂導線扭轉及翻轉特性研究[D]. 杭州: 浙江大學, 2019.

[27] Skelton P, Poots G. Snow accretion on overhead line conductors stiffness[J]. Cold Regions Science and Technology, 1991(19): 301-316.

[28] Fu Ping, Gilles B, Farzaneh M. Simulation of ice accumulation on transmission line cables based on time-dependent airflow and water droplet trajectory calculations[C]//Asme International Conference on Offshore Mechanics & Arctic Engineering, Vancouver, CA, 2004: 971-977.

[29] Nigol O, Buchan P. Conductor galloping-part Ⅱ torsional mechanism[J]. IEEE Transactions on Power Apparatus and Systems, 1981, PAS-100(2): 708-720.

Analysis of Interaction Mechanism between Icing and Torsion of Single Transmission Lines

Han Xingbo1Wu Haitao2Guo Sihua2Jiang Xingliang3Wang Yujie4

（1. Chongqing Engineering Laboratory for Transportation Engineering Application Robot Chongqing Jiaotong University Chongqing 400074 China 2.State Grid Chongqing Electric Power Company Chongqing Electric Power Research Institute Chongqing 401123 China 3. State Key Laboratory of Power Transmission Equipment & System Security and New Technology Chongqing University Chongqing 400044 China 4. School of Mechatronics and Vehicle Engineering Chongqing Jiaotong University Chongqing 400074 China）

Icing threatens the safe and stable operation of transmission lines. Accurate prediction of the icing process of conductor can help the work of anti-icing and disaster reduction of transmission lines. Generally, the icing of conductor is accompanied by the torsion process of conductor. Because of the interaction of conductor torsion and icing, there is a big difference of the icing shape and rate between different positions on conductors. In order to improve the accuracy of numerical calculation of conductor icing, a dynamic numerical calculation model of conductor icing torsion is established based on hydrodynamics and basic mechanics of conductor torsion in this paper. Comprehensively, the model takes the effects of torsion angles and torsion icing shapes on the icing process of conductor into consideration, including the effects on the trajectories of water droplets in the air. Through the simulation, the change law of torsion of three different types of conductors after icing at different positions and the influence of conductor torsion on icing are analyzed. The results show that the torsion angle of the conductor increases from both ends to the center after icing; compared with the untwisted conductor, the droplet collision range and icing rate of the twisted conductor are larger; and there is a great difference between the icing shape at the end and the center of twisted conductors. The icing shape at the end of conductors tends to be wing shaped while the icing shape tends to be a cylinder at the middle. When the wind velocity and the median volume diameter of water droplets are both large, the icing rate of conductors with a larger diameter under torsion condition is faster.

Conductor, icing, torsion

10.19595/j.cnki.1000-6753.tces.211098

TM85

交通工程應用機器人重慶市工程試驗室開放基金（CELTEAR-KFKT-202106）、重慶市教育委員會科學技術研究計劃項目（KJQN202000727）和國家自然科學基金重點項目（51637002）資助。

2021-07-19

2021-11-10

韓興波 男，1992 年生，博士研究生, 研究方向為復雜大氣環境下輸電線路外絕緣及防護。E-mail：hanxingbocqu@163.com（通信作者）

吳海濤 男，1991年生，碩士，工程師, 研究方向為架空輸電線路運檢、在線監測、故障診斷等。E-mail：978201734@qq.com

（編輯 赫蕾）