振動基柔順驅動打磨機器人的力/位混合控制研究

尤子成，王志剛，郭宇飛

(1.武漢科技大學，冶金裝備及其控制教育部重點實驗室，湖北武漢 430081;2.武漢科技大學，機器人與智能系統研究院，湖北武漢 430081)

0 前言

隨著對機器人技術研究的不斷加深，打磨機器人廣泛應用于磨削加工領域。機器人打磨相比于人工打磨具有連續工作時間長、效率高等優點。通過對打磨機器人進行力控制或者位置控制可提升打磨精度，保證打磨件質量。國內外學者對機器人打磨加工的研究主要集中在打磨機制和工藝、軌跡規劃、力控制算法及系統開發等幾個方面。

打磨機器人不僅要求其末端打磨機構能按照預定的軌跡行走，更要求其打磨機構對加工件保持恒力打磨。目前，主要的力控制方法分為力/位混合控制與阻抗控制。這兩種方法都是通過主動控制方式，使打磨機構與加工件接觸時存在柔順特性。阻抗控制是將機械臂系統建立為等效阻抗模型，當機械臂末端與環境產生接觸力時或實際運動軌跡發生偏差時，阻抗模型會產生反饋信號對位置或力進行調節。力/位混合控制是將機械臂末端在笛卡爾坐標系下進行正交分解，在2個子方向上分別進行力控制和位置控制。文獻[9]采用滑模控制對力進行控制，可在外界環境剛度突然發生變化的情況下保持恒力打磨。文獻[10]采用模糊PID控制算法提高了接觸力穩定性。

打磨機器人通常被安裝在固定基座上對打磨件進行打磨，但對于大型的加工件，如飛機葉片、航天器機身、薄壁工件等，打磨機器人在打磨拋光作業時需移動打磨。然而，移動打磨會產生基礎振動從而影響打磨、拋光精度，同時長時間打磨會對關節造成損傷。文獻[11]在機械臂末端添加智能執行器以控制接觸力，達到抑制振動的效果。文獻[12]對受到振動的機械臂采取分段線性反饋控制，減少了振動造成的影響。

在打磨機器人加工過程中，機械臂末端與環境之間會產生持續性碰撞，接觸力反饋回關節，從而對關節造成一定的損傷。為避免機械臂關節的損傷，在機械臂末端與電機之間添加扭簧柔順裝置即串聯彈性驅動器(Series Elastic Actuators,SEA)。文獻[16]中空間機器人在捕獲其余航天器過程時，通過在電機與關節之間串聯彈性驅動器及自抗擾控制方案，避免了關節受到沖擊力。文獻[17]設計了一種彈簧阻尼緩沖裝置，避免關節受到載荷沖擊被破壞。但添加彈簧類裝置也會造成關節的振動，需對柔性關節的振動進行抑制。學者們對此進行了許多研究，奇異攝動法是重要方法之一。通過奇異攝動法可將剛柔耦合系統分為不同時間尺度的2個子系統，分別對它們設計控制器，從而實現系統的控制。文獻[18]對傳統SEA機械臂進行改進，采用干擾觀測器提高系統的魯棒性。文獻[19]對柔性空間機械臂系統引入奇異攝動法，將系統分為快、慢2個子系統，慢變子系統采用狀態觀測器進行控制，快變子系統采用差值反饋法進行控制，抑制了系統的彈性振動及外部干擾。

本文作者針對打磨機器人，考慮基礎振動、轉動關節柔性，建立打磨機器人動力學模型。采用奇異攝動法將系統分為快、慢2個子系統，快變子系統采用速度差值反饋控制法，慢變子系統采用力/位混合控制。力/位混合控制中，力控制采用PID控制，位置控制采用神經網絡魯棒控制器控制，研究打磨機器人在基礎振動的情況下，保持恒力打磨及軌跡的準確跟蹤。

1 打磨機器人建模與奇異攝動模型

1.1 打磨機器人動力學模型

以柔性關節剛性臂打磨機器人為研究對象，打磨機構與機械臂末端相連，其簡化模型如圖1所示。柔性關節處的電機輸出軸與關節部分通過線形扭簧連接，如圖2所示。

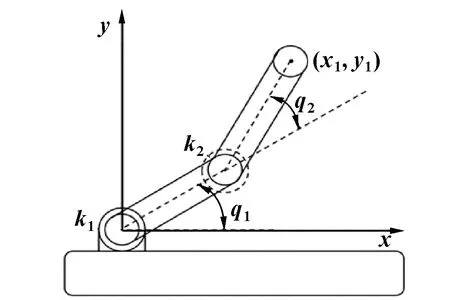
圖1 機械臂簡化模型示意

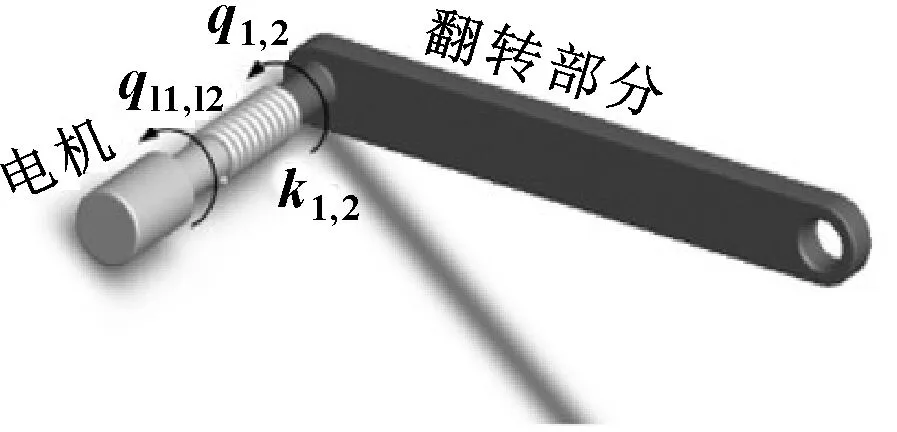
圖2 柔性關節簡化示意

基于以上簡化模型，用拉格朗日法建立動力學方程為

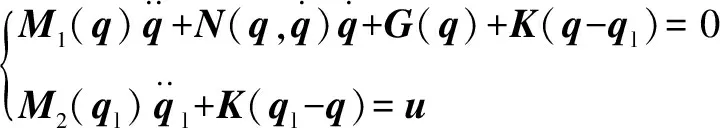
(1)

其中:()為慣性矩陣；()為離心力和哥氏力矩陣；()為系統重力矩陣；為傳動部分的剛度矩陣；()為轉動關節柔性產生的附加慣量矩陣，也是一個正定對稱矩陣；為柔性關節產生的附加坐標;為關節的角位移；為驅動力向量。各項表達式分別為

=

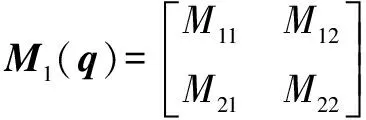
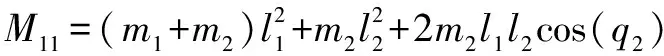
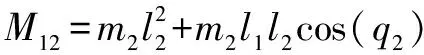
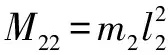
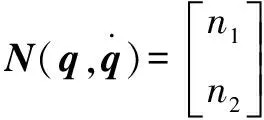
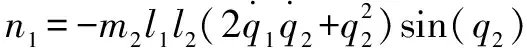
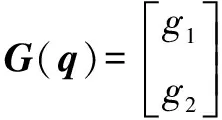
=(+)cos()+cos(+)

=cos(+)

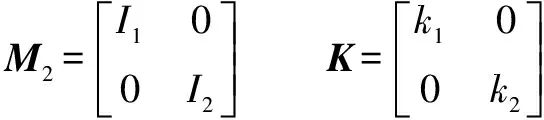
式中：、分別為關節1和2處等效到電機軸的轉動慣量。

1.2 奇異攝動模型

柔性關節的轉動會引起系統的彈性振動，因而會對系統的位置控制以及力控制產生影響。所以，針對打磨機器人系統設計的控制率不僅要保持力控制和位置控制的穩定，還要抑制柔性關節所引起的振動。在系統中引入奇異攝動法，將剛柔耦合系統分解為快、慢2個時間尺度子系統，分別對這2個子系統設計控制率，最后將慢變控制率與快變控制率相加可得到系統的總控制率。

定義柔性力變量為

=(-)

(2)

引入攝動參數，定義新的剛度矩陣：

=

(3)

將柔性力變量和新剛度矩陣代入式(1)，求得系統的奇異攝動模型為

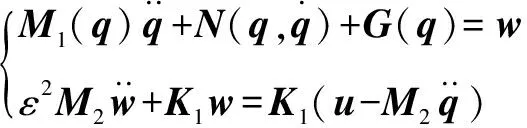
(4)

分別對奇異攝動模型中的快、慢子系統進行求解。

1.2.1 慢時變子系統

由式(4)可知，令攝動參數=0,可求得慢時變剛性系統變量為

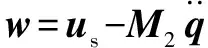
(5)

將式(5)代入式(4)中的第1個公式，可以得出慢時變子系統的動力學方程：

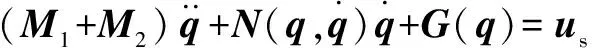
(6)

通過對比剛性二自由度機械臂模型，可知在不考慮柔性的前提下，慢時變子系統動力學方程與前者一致。

1.2.2 快時變子系統

將式(4)中的第1個公式進行變形得：

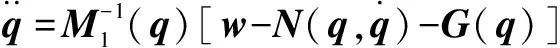
(7)

將式(7)代入式(4)的第2個公式，得：

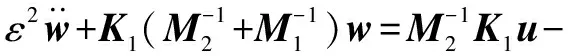
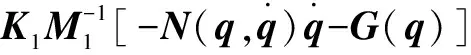
(8)

將=0代入式(8)，可得：

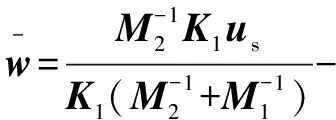
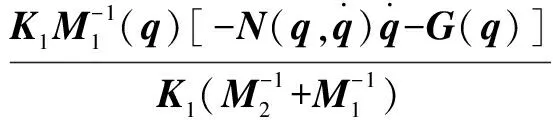
(9)

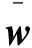
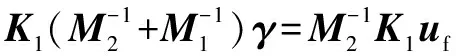
(10)

式中：=-為快時變子系統的廣義控制量。

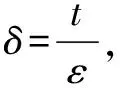
(11)

2 控制器的設計

2.1 混合控制

通過前文可知，只需將快、慢2個子系統的2個控制率相加即可得到系統的控制率：

=+

(12)

通過慢時變子系統控制率，實現打磨機器人的力控和位置控制；通過快時變子系統控制率實現柔性關節的振動抑制。混合控制器原理如圖3所示。

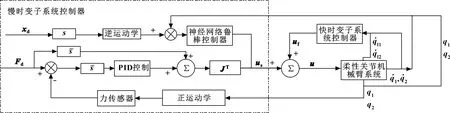
圖3 打磨機器人混合控制原理

2.2 快時變子系統的控制率

分別對快、慢子系統進行設計，設計的快時變子系統的控制率為

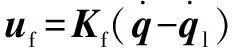
(13)

式中：=/,為正定對角矩陣。根據關節的實際角速度與電機輸出的角速度差對系統進行反饋控制，以保證系統穩定。

2.3 慢時變子系統的控制

由前述可知，采用奇異攝動法對系統進行分解，分解后的慢時變子系統與剛性系統無區別。針對打磨機器人在工作中會受到振動的影響，利用力/位混合控制對打磨機進行力控和位控，在位置控制中提升系統的控制精度和魯棒性。

2.3.1 力控制

將打磨機器人末端與環境的接觸模型等效于彈簧模型，由胡克定律可知：

=(-)

(14)

式中:為環境剛度;為打磨頭在工作空間的實際位置;為打磨頭在打磨件上的位置。

由于機械臂與環境存在接觸，為保持機械臂的穩定工作狀態，需對關節角施加一定的關節扭矩，則可將機械臂力控環的動力學方程由式(6)改寫為

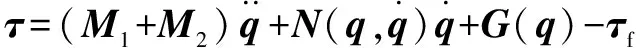
(15)

式中：為接觸力通過雅可比矩陣映射在關節空間上的扭矩。接觸力與驅動力矩的關系為

=

(16)

式中:為雅可比矩陣的轉置矩陣，具體公式為

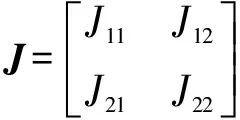
=-sin()-sin(+)

=-sin(+)

=cos()+cos(+)

=cos(+)

對力控環采用PID控制方法進行控制，式(16)改寫為

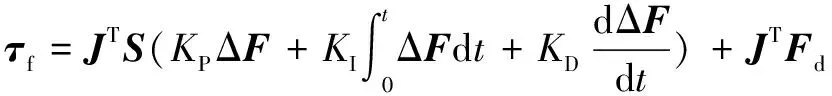
(17)

式中:、、分別為PID控制的3個參數；為選擇矩陣；為理論輸入力。

2.3.2 實際工作空間位置與關節的轉換

為方便對打磨機器人進行控制，需將笛卡爾坐標系下機械臂末端運動軌跡轉換至關節坐標系下表示。由圖1可得關節角位移和與機械臂在實際工作空間中的坐標和之間的關系：

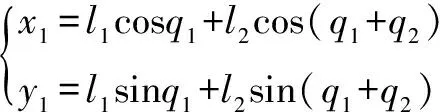
(18)

由式(18)可得：

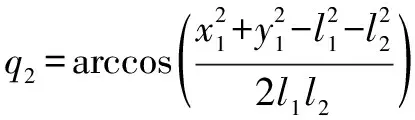
(19)

根據余弦定理以及的位置關系可得：

(20)

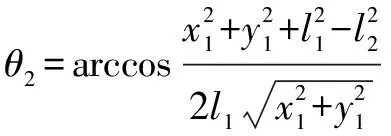
(21)

可得：

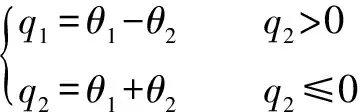
(22)

2.3.3 位置控制

為避免基礎振動對位置控制的干擾，在式(6)的基礎上引入干擾項，新的動力學方程為

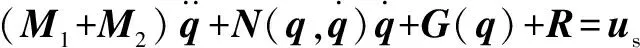
(23)

式中:為干擾項。

令=+,將式(23)變形為

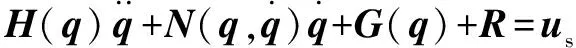
(24)

定義跟蹤誤差=-，為理論關節角，設計前饋控制率為

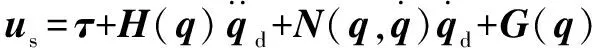
(25)

式中:為反饋控制率。將式(25)代入式(24)中得：

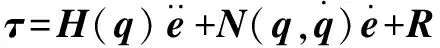
(26)

使用RBF神經網絡對擾動進行逼近：

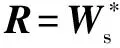
(27)

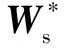
將式(27)代入式(26)中得：

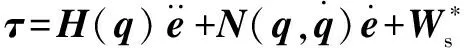
(28)

定義1:

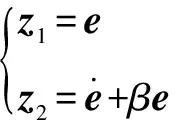
(29)

式中:為常數且大于0。

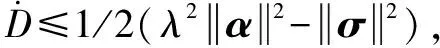
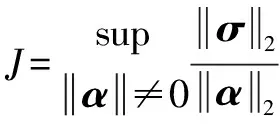
(30)

式中:是的范數，越小，系統的魯棒性越好。

(31)

將式(28)代入式(29)，得：

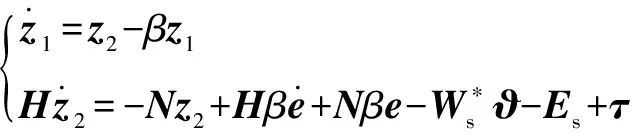
(32)

式(32)可化簡為式(31)的格式，具體變量如下：

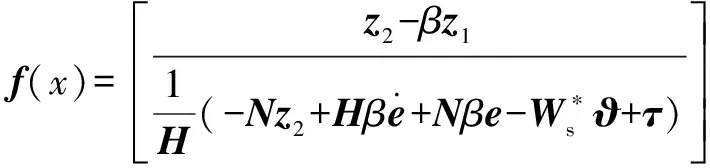
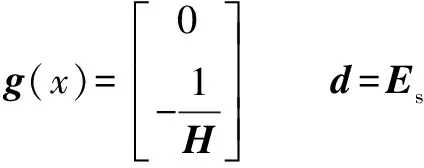
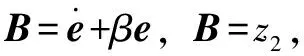
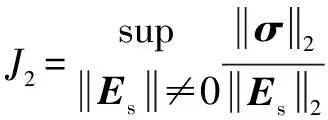
設計慢時變子系統設計自適應調整率為

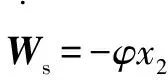
(33)

式中:為大于0的常數。

設計反饋系統的控制率為

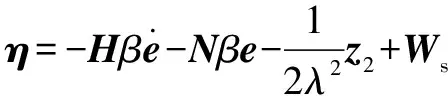
(34)

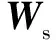
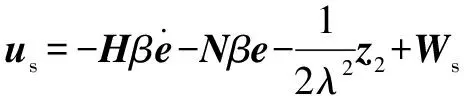
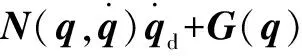
(35)

2.3.4 穩定性證明

對系統的穩定性進行證明，定義Lyapunov函數為

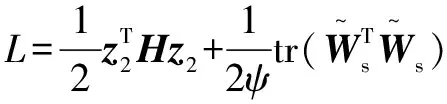
(36)

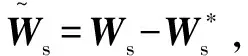
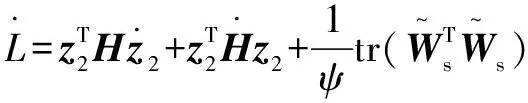
(37)

將式(32)中的第2個公式與式(33)代入式(37)得：

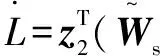
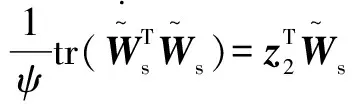
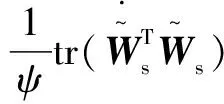
由HJI定理，可定義：

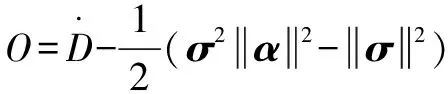
(38)

則有：

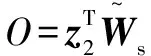
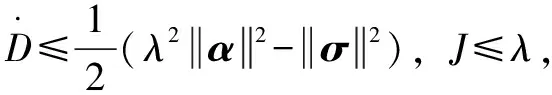
3 仿真與分析

為驗證所設計的控制器對存在基礎振動時打磨機器人控制的有效性，設計2組數值仿真實驗，采用MATLAB/Simulink進行對照分析。第1組：基礎振動時，快變控制器打開，慢變控制器中位置控制設置為PD控制，力控制設置為PID控制，檢驗機械臂末端在工作空間的軌跡跟蹤、關節1位置跟蹤、關節2位置跟蹤以及力的恒定效果；第2組：存在基礎振動時，通過關、開快變子系統，設置慢變子系統控制器中位置控制率為神經網絡魯棒控制器，力控為PID控制器，檢驗系統能否抑制基礎振動，實現對期望軌跡和期望力的跟蹤響應。施加的基礎振動信號如圖4所示，系統模型所取的參數和神經網絡參數如表1所示。

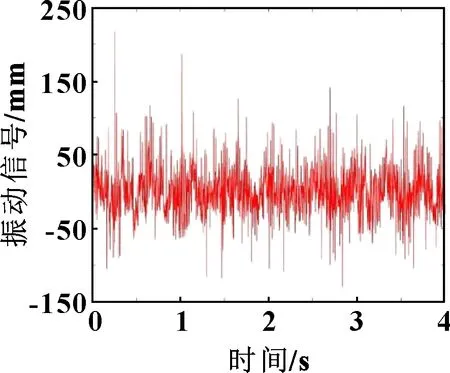
圖4 振動信號

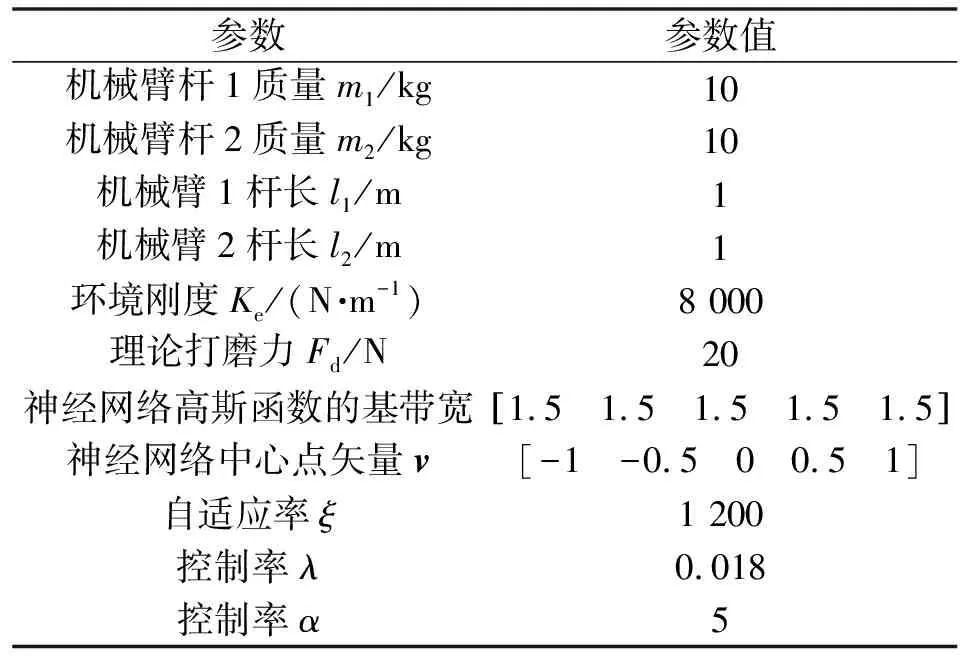
表1 系統模型參數與神經網絡參數

圖5—圖8所示為位置控制為PD控制時，機械臂末端理論軌跡跟蹤、關節1(qd1)位置跟蹤、關節2(qd2)位置跟蹤、期望力的跟蹤結果。可知:打磨機器人在作業時，PD控制對振動的振幅和頻率有一定的抑制效果，但是其軌跡跟蹤出現明顯的波動，跟蹤效果不理想，與此同時力跟蹤出現了明顯的超調。

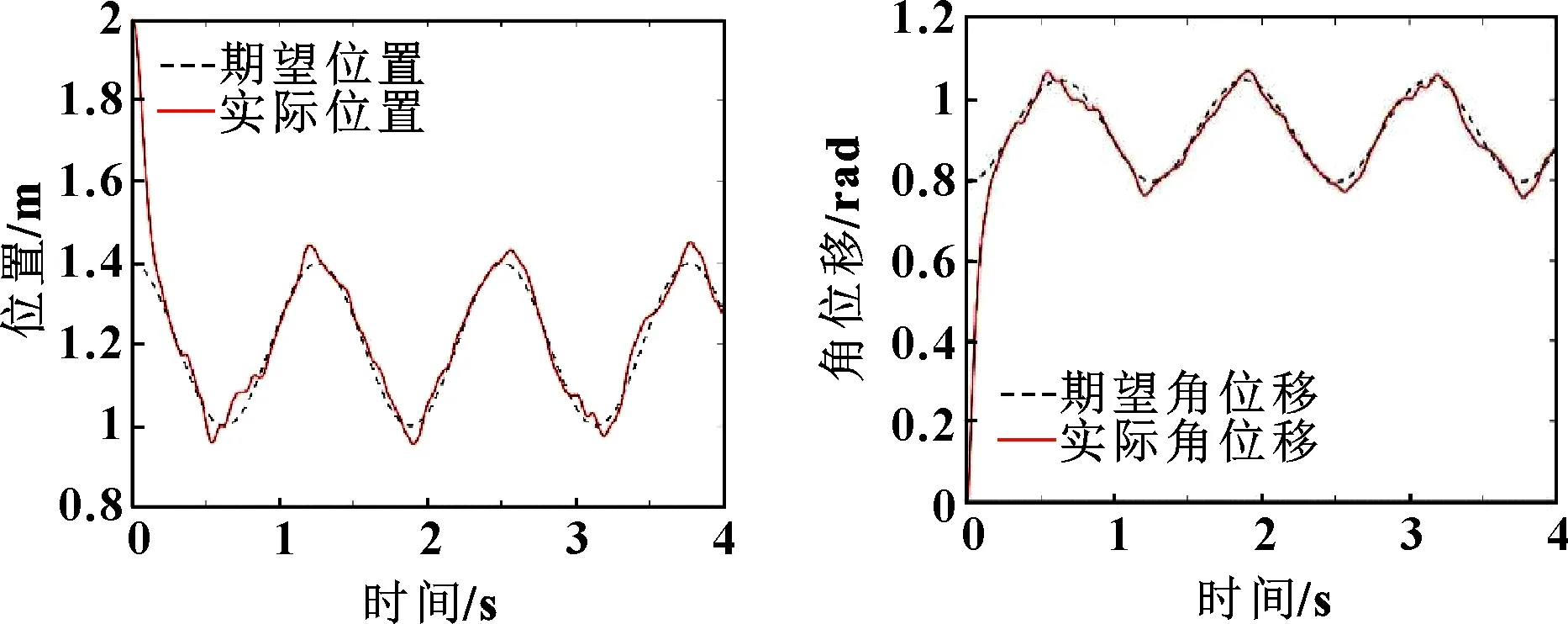
圖5 PD控制時機械臂末端位置跟蹤 圖6 PD控制時關節1位置跟蹤

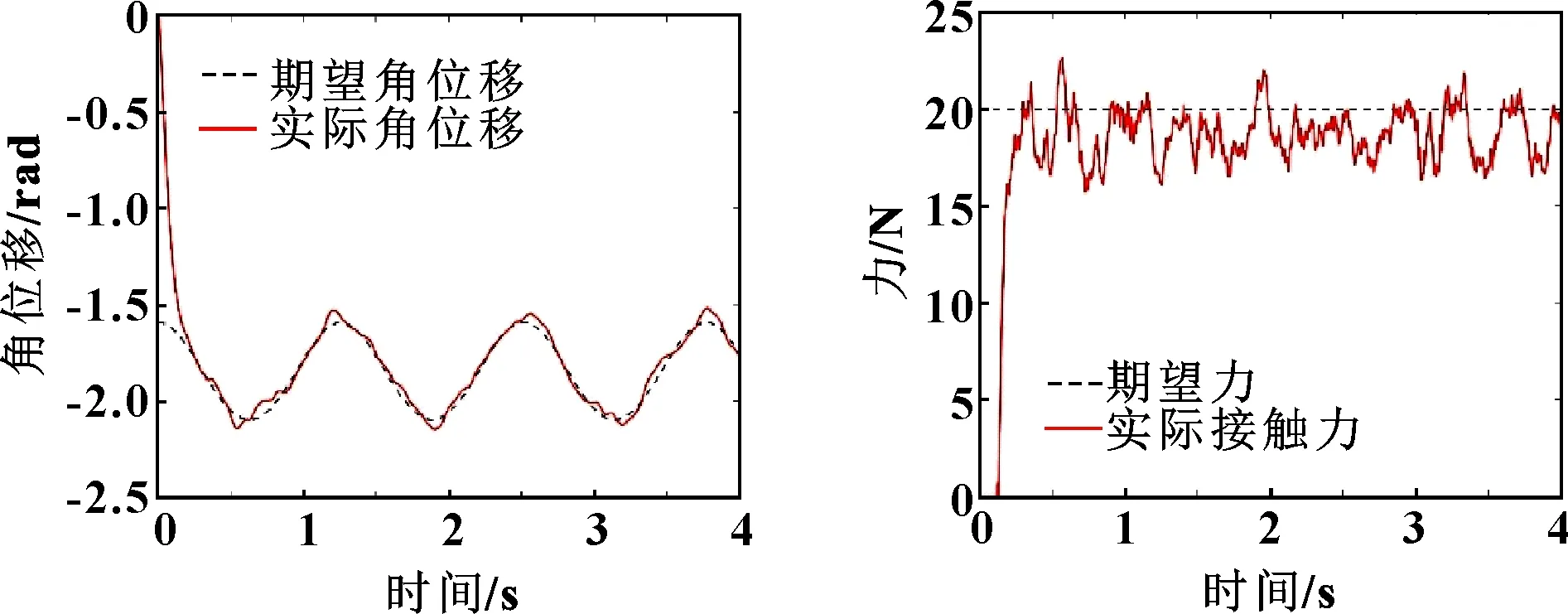
圖7 PD控制時關節2位置跟蹤 圖8 PD控制時力跟蹤

圖9—圖12所示為關閉快時變控制器時機械臂的位置、關節、力跟蹤結果。可知：不控制柔性關節振動時，軌跡跟蹤及關節1和關節2的位置跟蹤明顯出現了持續的振動，且打磨力出現明顯的超調和振動，但相比于PD控制，神經網絡魯棒控制器對基礎振動有著較強的抑制能力，其實際末端軌跡可較好地跟蹤理論軌跡。

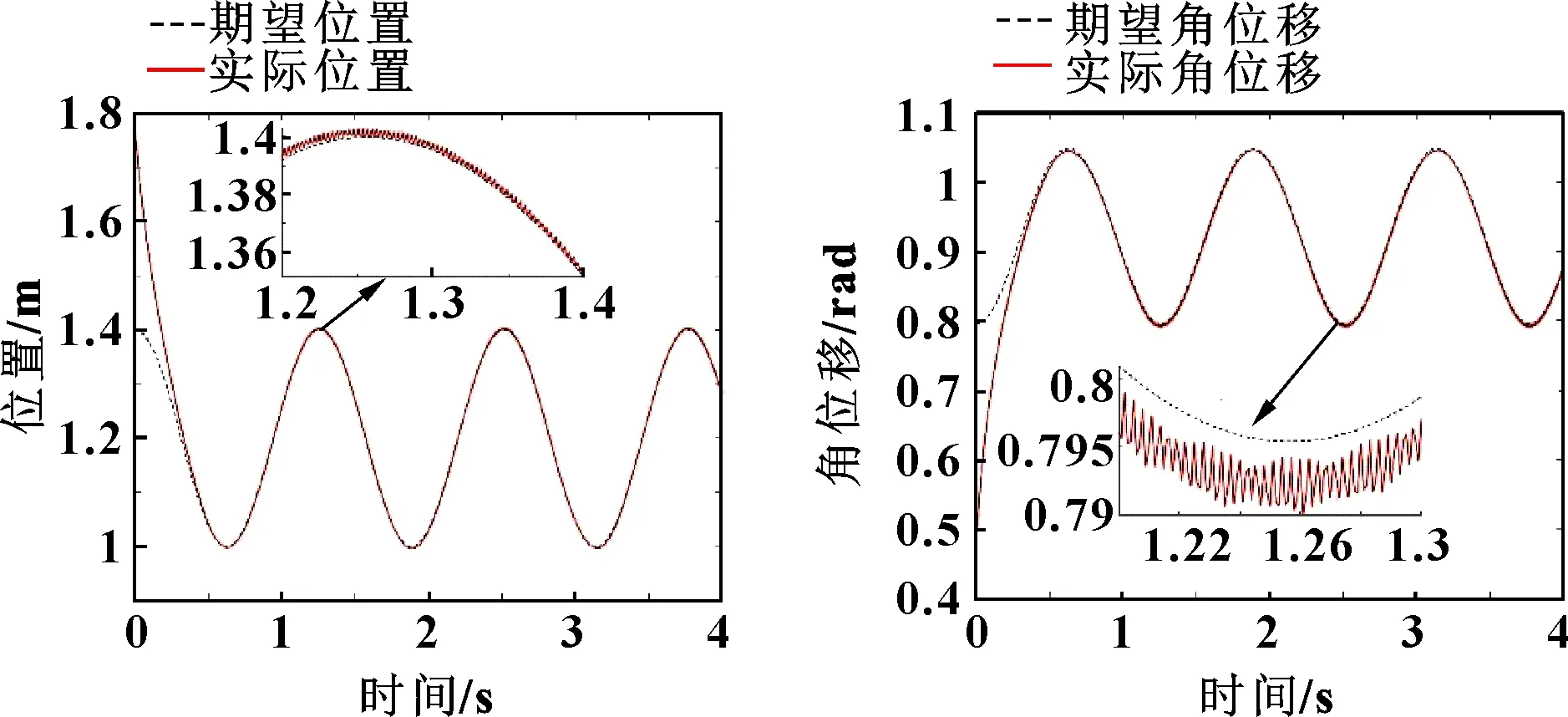
圖9 快變控制器關閉時機械臂末端位置跟蹤 圖10 快變控制器關閉時關節1位置跟蹤

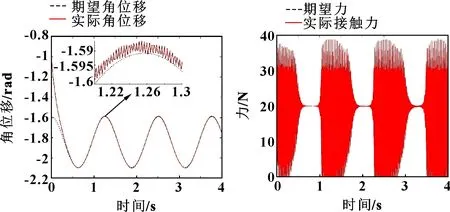
圖11 快變控制器關閉時關節2位置跟蹤 圖12 快變控制器關閉時力跟蹤

圖13—圖16所示為開啟快變控制器時機械臂末端的位置、關節、力跟蹤結果。可知：機械臂末端軌跡及關節1和關節2有著精確的跟蹤效果，相比于關閉快變控制器時軌跡跟蹤的效果，快變控制器開啟時對柔性關節的振動有很好的抑制作用；其接觸力保持在(20±0.1)N內(20 N為理論力)，滿足工作要求，保證了加工件的質量。

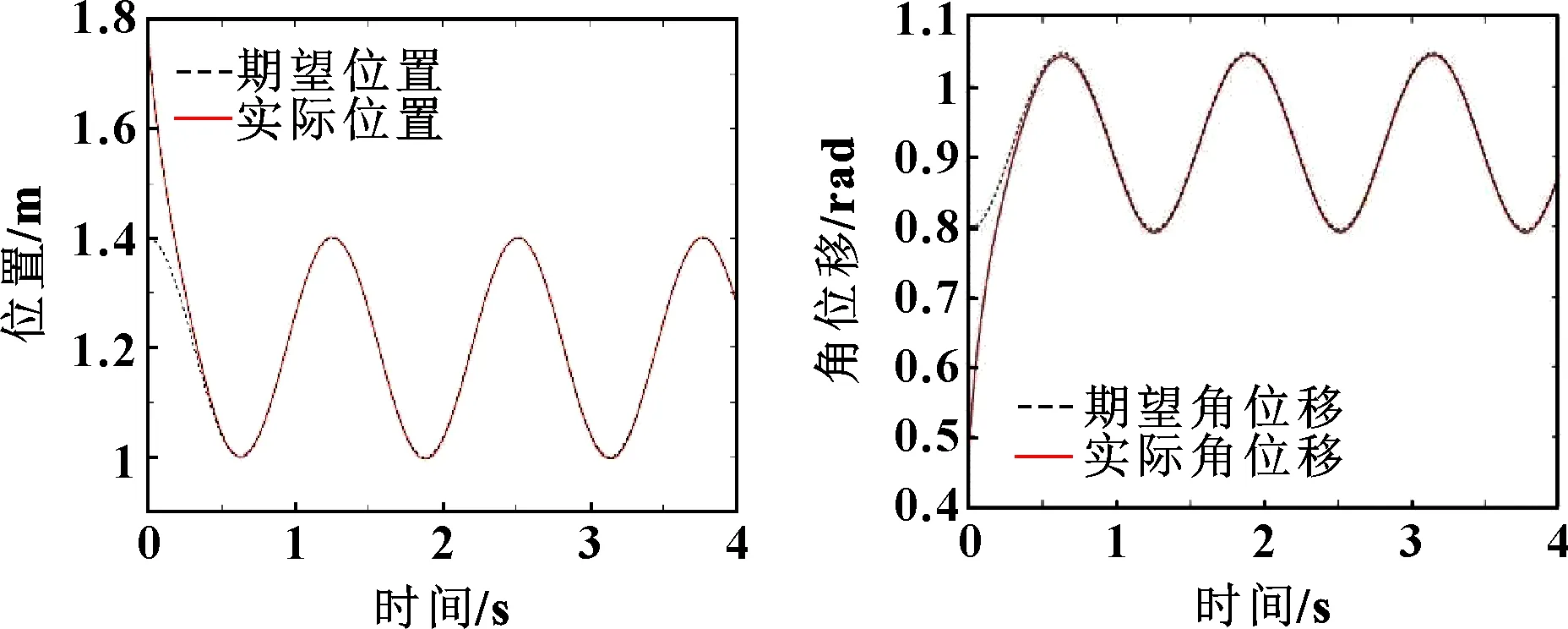
圖13 快變控制器打開時機械臂末端位置跟蹤 圖14 快變控制器打開時關節1位置跟蹤

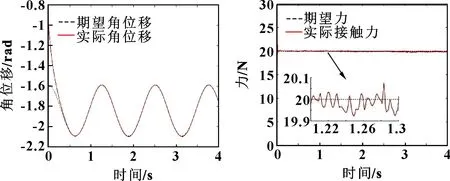
圖15 快變控制器打開時關節2位置跟蹤 圖16 快變控制器打開時力跟蹤

4 結束語

對存在外界基礎擾動及關節受到力沖擊的打磨機器人控制進行了研究，主要結論如下：

(1)在打磨機器人的實際作業中，需保持恒力打磨，但在受到基礎振動后，通過傳統PD或PID控制難以抑制振動，軌跡跟蹤和力跟蹤都出現了明顯的超調，而通過神經網絡魯棒控制器可以對振動造成的干擾進行抑制，達到工作要求；

(2)在傳統剛性打磨機器人的基礎上添加柔順驅動，緩沖了機械臂末端與環境接觸時的碰撞力，減少對打磨機器人關節的損傷。但柔順驅動的引入帶來了柔性關節的振動，可以通過奇異攝動法設計控制器對振動進行抑制。結果表明：所設計的控制器能克服打磨機器人在作業時受到的振動影響及抑制柔性關節的振動，實現打磨機器人的軌跡跟蹤和恒力打磨。