風機齒輪箱軸承應力及疲勞壽命分析

白浩宇， 穆塔里夫·阿赫邁德，2，白云松，鞠增鑫

(1.新疆大學機械工程學院，新疆烏魯木齊 830047；2.新疆大學電氣工程學院，新疆烏魯木齊 830047)

0 前言

在風力發電機組中，增速齒輪箱是重要的部件之一，其運行狀況的好壞與風力發電機運轉密切相關。由于齒輪箱的工作環境十分惡劣，導致齒輪箱中輸出軸端軸承受到復雜的載荷及劇烈的振動。根據數據統計，風電機組故障中齒輪箱失效占12%，而其中約50%為滾動軸承失效。由于密封差、潤滑不足及變載荷，齒輪箱中滾動軸承各部件會出現疲勞點蝕、剝落等故障。因此，研究具有一定缺陷故障軸承的應力與疲勞壽命，對滾動軸承穩定運行和故障檢測具有重要意義。

針對局部剝落缺陷軸承的動力學研究，國內外學者都進行了大量的相關工作。LIU等總結出一種改進的角接觸球軸承動力學模型，研究了速度、負載和缺陷尺寸對角接觸球軸承聲學特性的影響。SINGH等采用顯式動力學軟件LS-DYNA對具有局部外滾道線剝落的滾動軸承的振動響應進行了數值模擬，并驗證了軸承顯式有限元模擬結果的正確性。剡昌鋒等在考慮彈流潤滑和滑動作用的前提下，建立有局部故障的軸承系統模型，進行動力學數值分析，并通過試驗與仿真結果進行對比。張慧玲和呂福玲對帶有點蝕缺陷的軸承的振動信號進行了數值模擬，并分析了其缺陷特征。涂文兵等建立了缺陷存在于軸承各部件上的數值模型，分析獲得了滾子與其他部件的接觸應力變化曲線，總結出缺陷對軸承各部件之間接觸規律的影響。

研究者們通過仿真及試驗對軸承疲勞壽命進行研究及預測。HE等在ABAQUS中建立了回轉軸承的有限元模型，得到了球與滾道之間的接觸應力，聯合軸承數值分析結果和FE-SAFE計算了疲勞壽命和損傷。ZHANG等提出了一種準動態動力學模型來研究角接觸球軸承在任意預緊力作用下的載荷分布，在此基礎上，計算了該軸承在運轉狀態下的疲勞壽命。趙斗生等建立關于柔性軸承及波發生器多體動力學的接觸模型，在數值分析出模型應力及變形的基礎上，用nCode-DesignLife分析其壽命。耿民等人基于高速列車中牽引電機的軸承實際工況，用ANSYS建立了軸承的接觸模型，考慮軸承各部件之間游隙變化引起的受載變化和應力集中，并提出了新的計算軸承壽命的方法。

本文作者以5 MW風力發電機齒輪箱輸出軸端的軸承為研究對象，建立無缺陷軸承和不同尺寸局部剝落缺陷的軸承數值模型。利用顯式動力學分析滾子進入外圈缺陷和退出外圈缺陷的應力變化；將各軸承應力結果導入疲勞軟件進行壽命計算，從而得出局部剝落缺陷尺寸擴展對軸承應力和疲勞壽命的影響規律。

1 軸承模型及邊界條件

1.1 幾何與數值建模

選為圓柱滾子軸承(NU2232E)，其幾何參數如表1所示。針對風機齒輪箱軸承的實際工況，對軸承模型進行一些簡化：不考慮軸承內圈、外圈的倒角，可以避免對軸承應力分布的影響；不考慮軸承徑向和軸向的游隙。

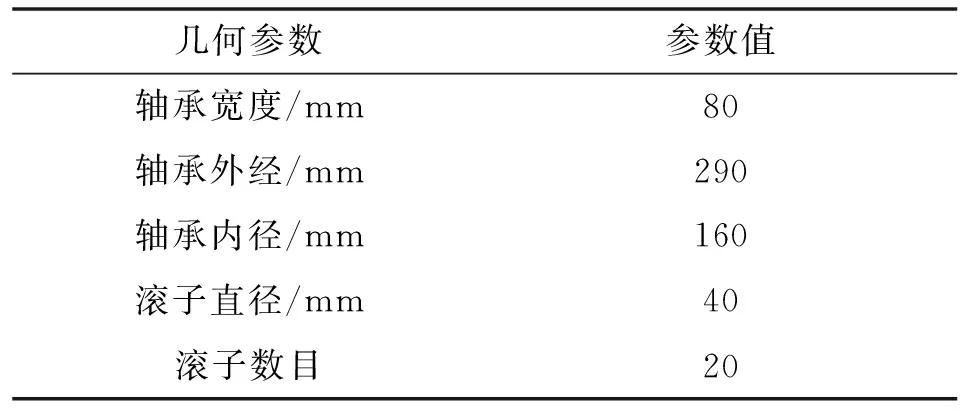
表1 NU2232E軸承參數

對模型進行有限元分析，先進行網格劃分，文中應用HyperMesh對圓柱滾子軸承進行網格劃分。軸承各部件均采用六面體網格，共計77 760個單元，如圖1所示。軸承各部件材料均采用軸承鋼，其材料參數：密度為7 820 kg/m，彈性模量為2.16×10MPa，抗拉強度為1 813 MPa，屈服強度為1 323 MPa。

圖1 NU2232E軸承數值模型

1.2 邊界條件

依據5 MW風機齒輪箱輸出軸端軸承的實際工況,限制外圈、、方向的移動和旋轉自由度，限制內圈方向的移動自由度和、方向的旋轉自由度。對內圈施加50 kN的徑向載荷和5種轉速(800、1 200、1 600、1 800、2 000 r/min)。滾子與內圈、外圈采用面與面接觸；不考慮保持架對軸承滾子的影響，將保持架設為剛體。為使軸承在開始時能夠穩定運轉，徑向載荷先作用，0.01 s后轉速和載荷同時作用，0.2 s時結束運轉。

2 軸承數值分析

2.1 局部缺陷建模

在實際中，軸承外圈局部剝落缺陷的形狀不規則，為方便劃分網格進行仿真，將外圈缺陷理想化為矩形，軸承未運轉之前，缺陷位于外圈上19號滾子與20號滾子之間，如圖2所示。

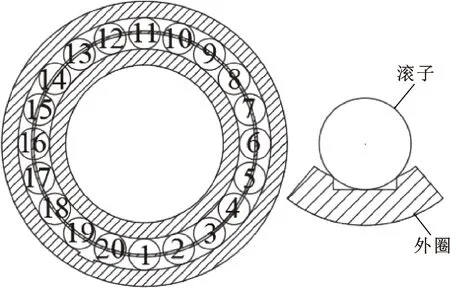
圖2 滾子與外圈局部剝落缺陷示意

矩形缺陷長度40 mm，深度0.3 mm，選取不同寬度尺寸1、3、4、6和7 mm，模擬缺陷擴展對軸承各部件動力性能的影響。

2.2 應力分析

有局部剝落缺陷(寬度、深度分別為7、0.3 mm)的軸承運轉過程中，滾子滾入外圈的缺陷和滾出外圈缺陷。選取無缺陷軸承和有缺陷軸承的1號滾子上與外圈接觸面中間的節點，提取節點應力曲線，進行應力分析。

在轉速800 r/min的情況下，軸承內圈受到徑向載荷和轉速的作用，有缺陷軸承和無缺陷軸承在0.12 s時的等效應力如圖3所示，其各部件最大等效應力如表2所示。在整個軸承運轉過程中，徑向載荷和轉速都是平滑加載，隨著徑向載荷和轉速隨時間不斷加大，有缺陷軸承的等效應力大于無缺陷軸承的等效應力，這是因為缺陷軸承在運轉到0.12 s時，滾子還未滾入缺陷，距離缺陷的邊緣較近。提取兩軸承1號滾子節點的等效應力曲線，如圖4所示。可以看出：運轉到0.12 s時，缺陷軸承滾子節點應力波動較大，這是由于其他滾子經過缺陷造成內圈受力偏載過大，1號滾子與內圈接觸發生偏移，從而使得有缺陷軸承滾子節點應力大于無缺陷軸承節點應力。

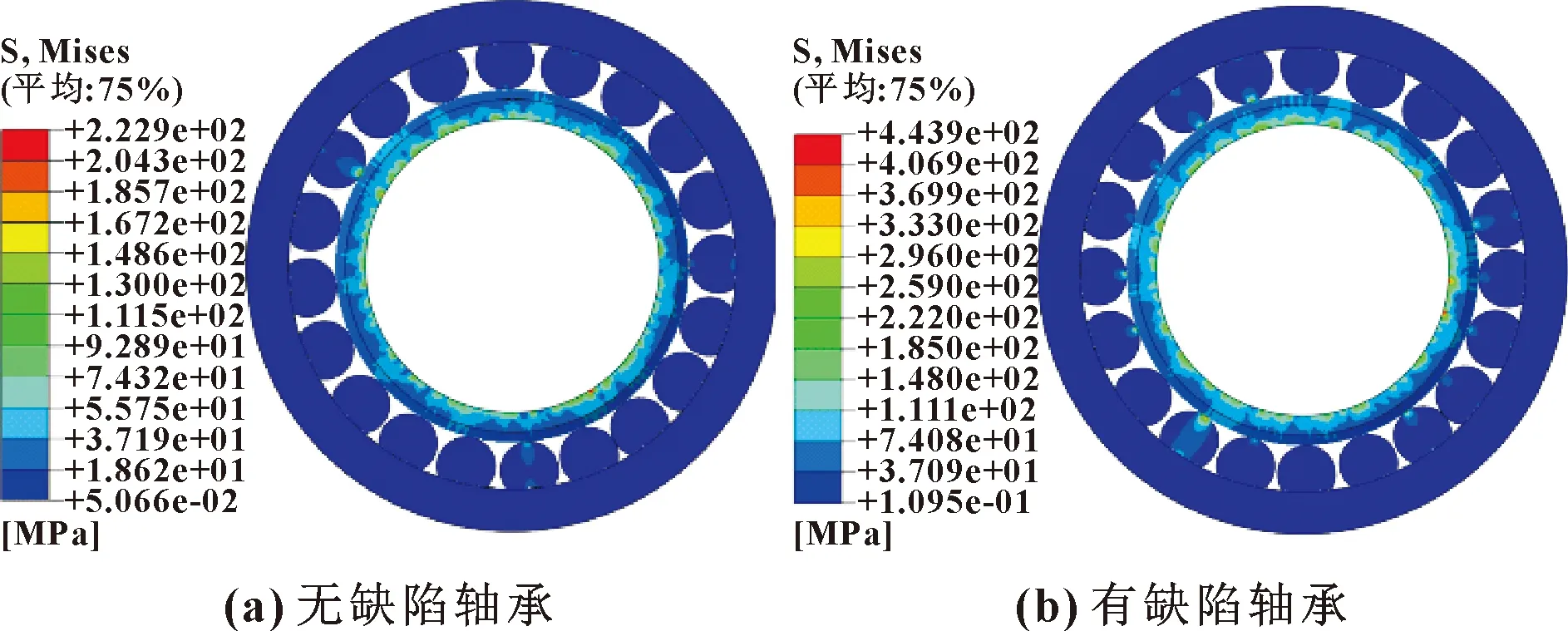
圖3 0.12 s時各軸承的等效應力云圖

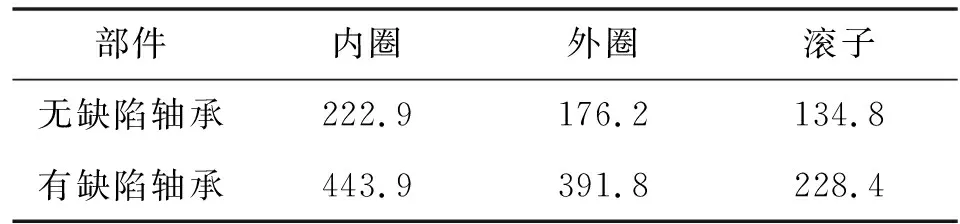
表2 軸承各部件在0.12 s時最大等效應力 單位：MPa

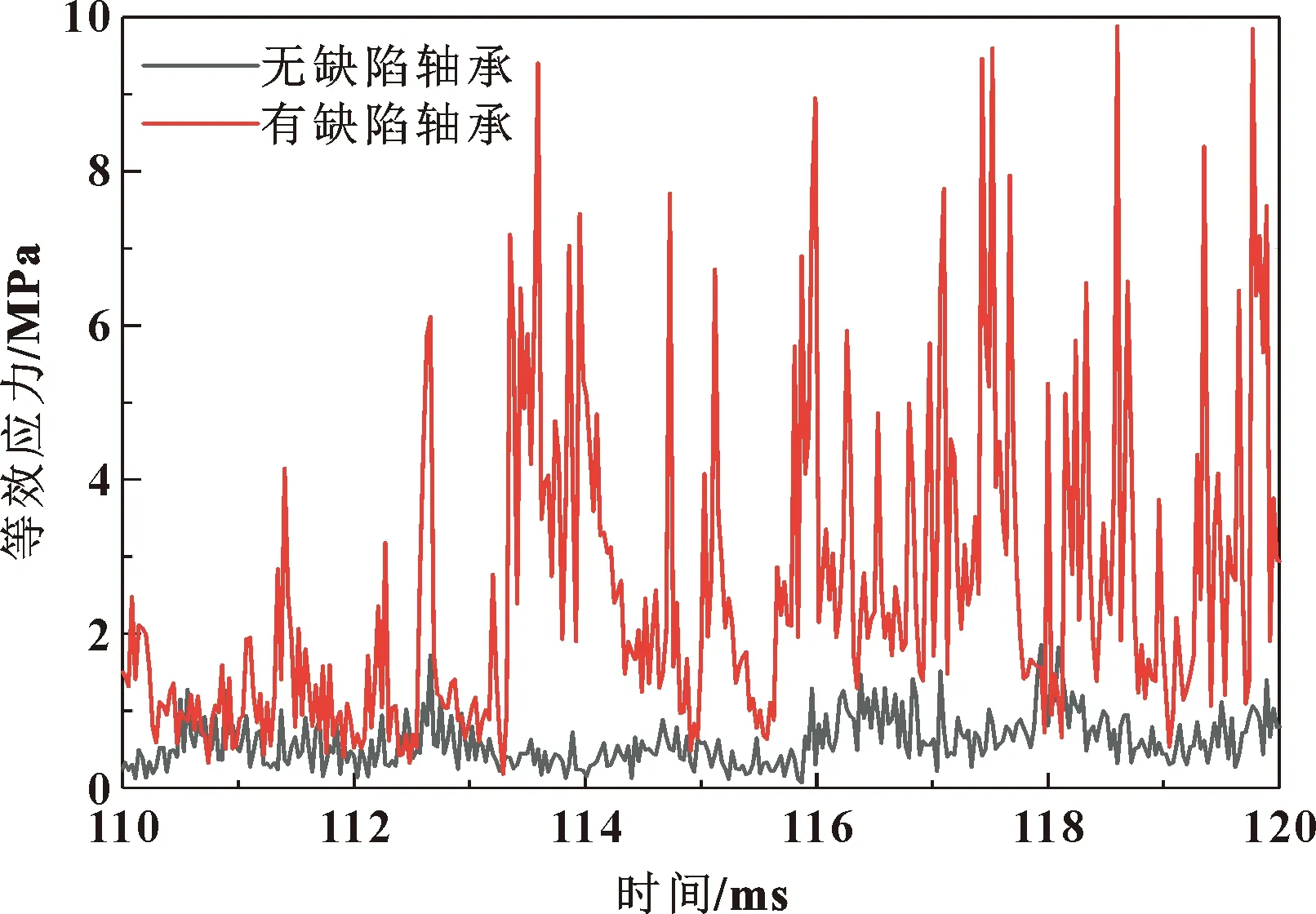
圖4 滾子節點在0.11～0.12 s時等效應力

圖5所示為有缺陷軸承和無缺陷軸承在0.13 s時的等效應力云圖。可以看出：等效應力較大的是有缺陷的軸承。這是由于有缺陷軸承運轉到0.13 s時，1號滾子準備滾入缺陷，與缺陷邊緣接觸，缺陷左邊緣出現應力集中(如圖6(a)所示)，0.14 s時滾子滾出缺陷，與缺陷右邊緣接觸，右邊緣出現應力集中(如圖6(b)所示)，使得載荷力無法作用在該滾子上，所以造成局部剝落缺陷軸承應力大的原因是缺少1號滾子來承受徑向載荷的作用，使得內圈受力不均。圖7所示為兩軸承的1號滾子節點等效應力曲線，可以看出1號滾子滾入和退出缺陷的應力變化過程，3次應力幅值波動分別對應滾入缺陷、在缺陷里和滾出缺陷這3個事件。

圖5 0.13 s時各軸承的等效應力云圖

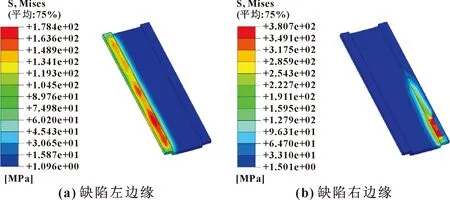
圖6 缺陷邊緣等效應力云圖

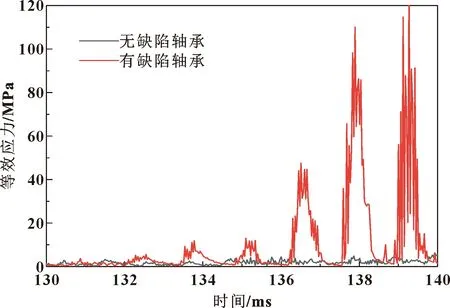
圖7 滾子節點在0.13～0.14 s時等效應力

不同轉速下無缺陷軸承和有缺陷軸承各部件的最大等效應力分別如圖8—圖10所示。可知：徑向載荷相同時，轉速越大，軸承各部件的等效應力越大，其中內圈應力變化趨勢最大，其次是滾子、外圈。隨著缺陷尺寸的擴大，外圈的應力也逐漸增大。在實際中，齒輪箱輸出軸端受到徑向載荷的作用傳遞給軸承內圈，由于外圈存在局部剝落缺陷，每個滾子在滾入和滾出缺陷時，使內圈出現偏載過大，造成內圈應力集中。

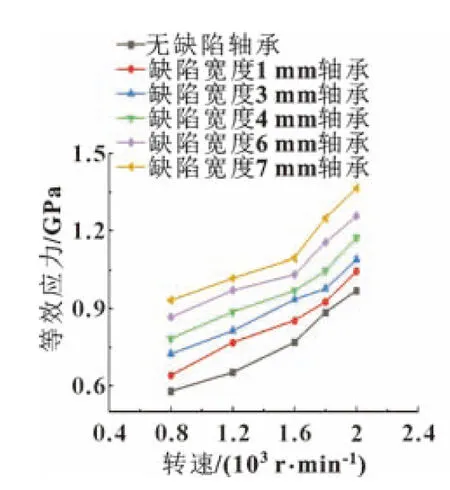
圖8 各軸承內圈最大等效應力

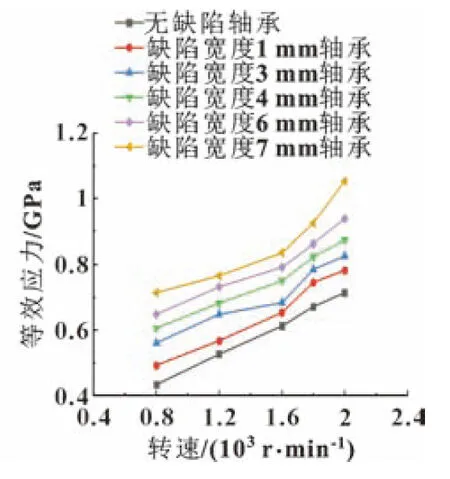
圖9 各軸承滾子最大等效應力

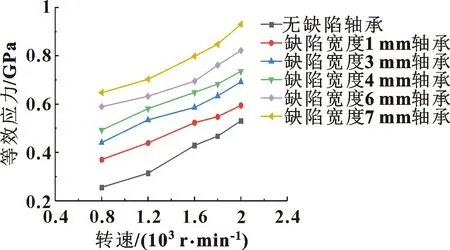
圖10 各軸承外圈最大等效應力

3 疲勞壽命分析

3.1 疲勞損傷機制

疲勞損壞是指零件在運行過程中受到載荷的沖擊從而發生損壞。在循環載荷施加于零件的作用過程中，零件上會產生應力集中區域，還會引起局部變形，從而使零件永久性損壞。另外，機構的運轉使循環次數逐漸上升，機構發生故障的可能性也會增加。當循環次數到了一定數值后，該機構就不能工作了，也就是失效。

3.2 疲勞損傷理論

為更加準確地分析風機齒輪箱輸出軸端軸承疲勞壽命，選用Palmgren-Miner累積損傷準則進行計算。在實際工況中，由于循環載荷對零件整體起作用，會引起零件材料損傷，而損傷的累積最終會使零件發生疲勞破壞。此理論中，損傷的大小與載荷的循環作用次數呈線性關系，而且零件失效時吸收的凈功和負載歷程都與零件的損傷無關。因此，可以推導出零件長期運轉后發生疲勞失效時的應力循環次數和吸收的凈功的關系為

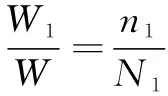
(1)

零件因次循環載荷作用產生各種應力，進而引起損傷，即：

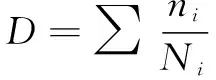
(2)

式中:為零件在級別應力循環加載的次數；為零件在級別循環負載引起疲勞失效時的次數。因循環負載的沖擊導致零件損傷大于等于1時(≥1)，認為該零件已被破壞。

3.3 結果分析

前人通過試驗總結出軸承疲勞壽命計算方法，分別是應變疲勞(E-N)和應力疲勞(S-N)。根據風電齒輪箱輸出軸端軸承實際運轉工況，軸承的運轉屬于高循環疲勞，所以采用名義應力法計算軸承疲勞壽命。仿真得到無缺陷軸承和局部剝落缺陷(寬度、深度分別為7、0.3 mm)軸承在轉速為800 r/min時的疲勞壽命和損傷云圖。

3.3.1 內圈疲勞分析

無缺陷軸承和有缺陷軸承內圈的疲勞壽命和損傷云圖分別如圖11、圖12所示。

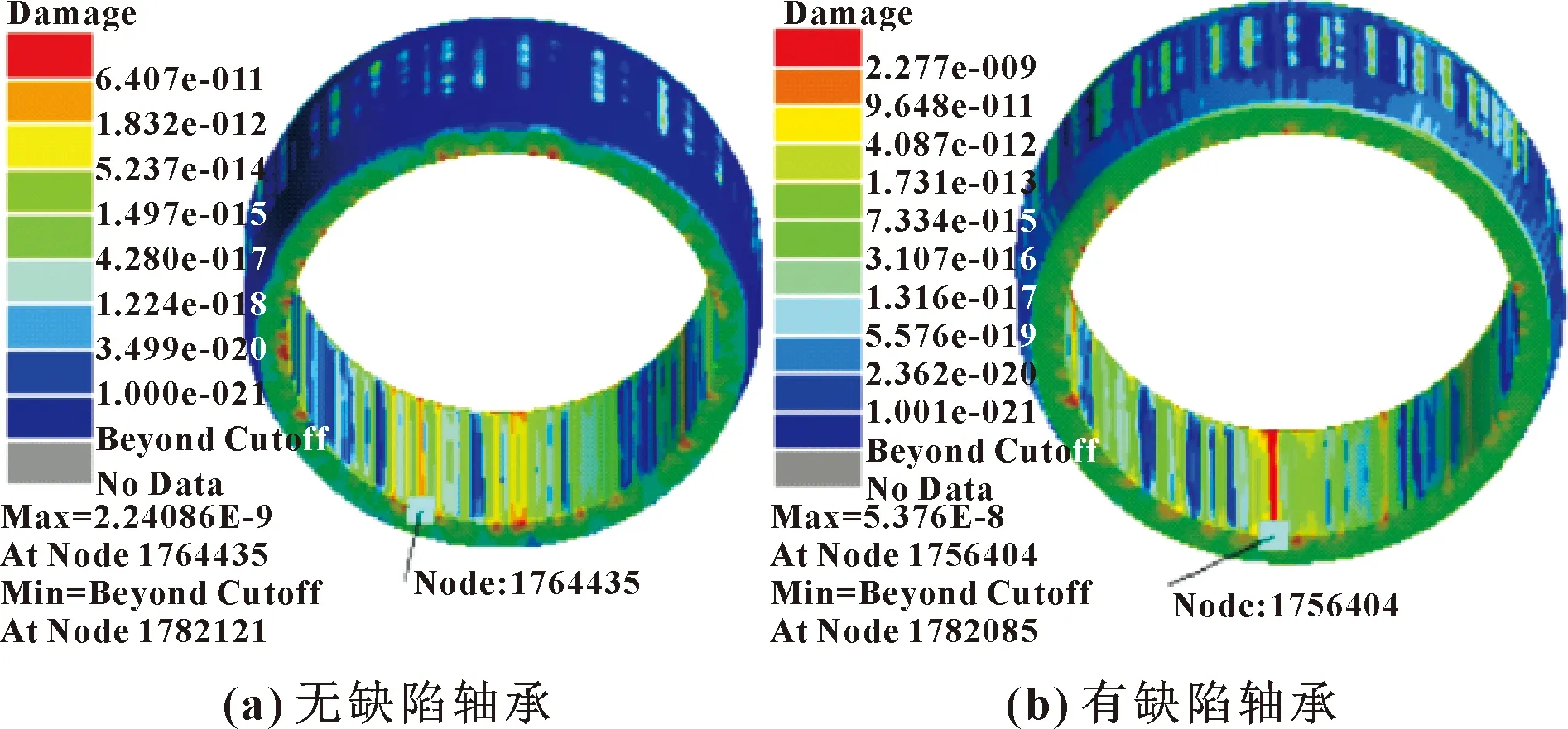
圖11 內圈損傷云圖

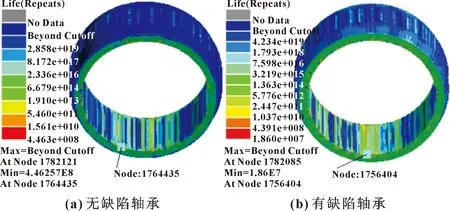
圖12 內圈疲勞壽命云圖

由圖11、圖12可知：無缺陷軸承內圈在節點N1764435處發生損傷，其最大損傷為2.240 86×10，在該節點處最小壽命為4.463×10次，而多數損傷在4.280×10～1.832×10，與之對應的疲勞壽命為2.336×10～5.460×10次；有缺陷軸承內圈在節點N1756404處發生損傷，其最大損傷為5.376×10，在該節點處最小疲勞壽命為1.860×10次，而多數損傷在3.107×10～4.087×10，與之對應的疲勞壽命為3.219×10～2.447×10次。軸承內圈內表面處發生損傷，從而可以獲知該區域會出現故障，因為內圈受到徑向載荷的作用，會出現應力集中，這與軸承動力學仿真結果內圈出現應力集中相符合。

由圖11、圖12還可以看出：在載荷和轉速的作用下，有缺陷軸承內圈的最大損傷比無缺陷軸承內圈的最大損傷大，而且有缺陷軸承內圈的疲勞壽命比無缺陷軸承的疲勞壽命小。這是由于缺陷軸承運轉時，滾子滾入和滾出外圈缺陷時，軸承內圈會出現偏載受力過大，造成內圈應力集中，導致發生損傷。

3.3.2 圓柱滾子疲勞分析

圖13、14所示分別為無缺陷軸承和有缺陷軸承圓柱滾子的損傷和疲勞壽命云圖。

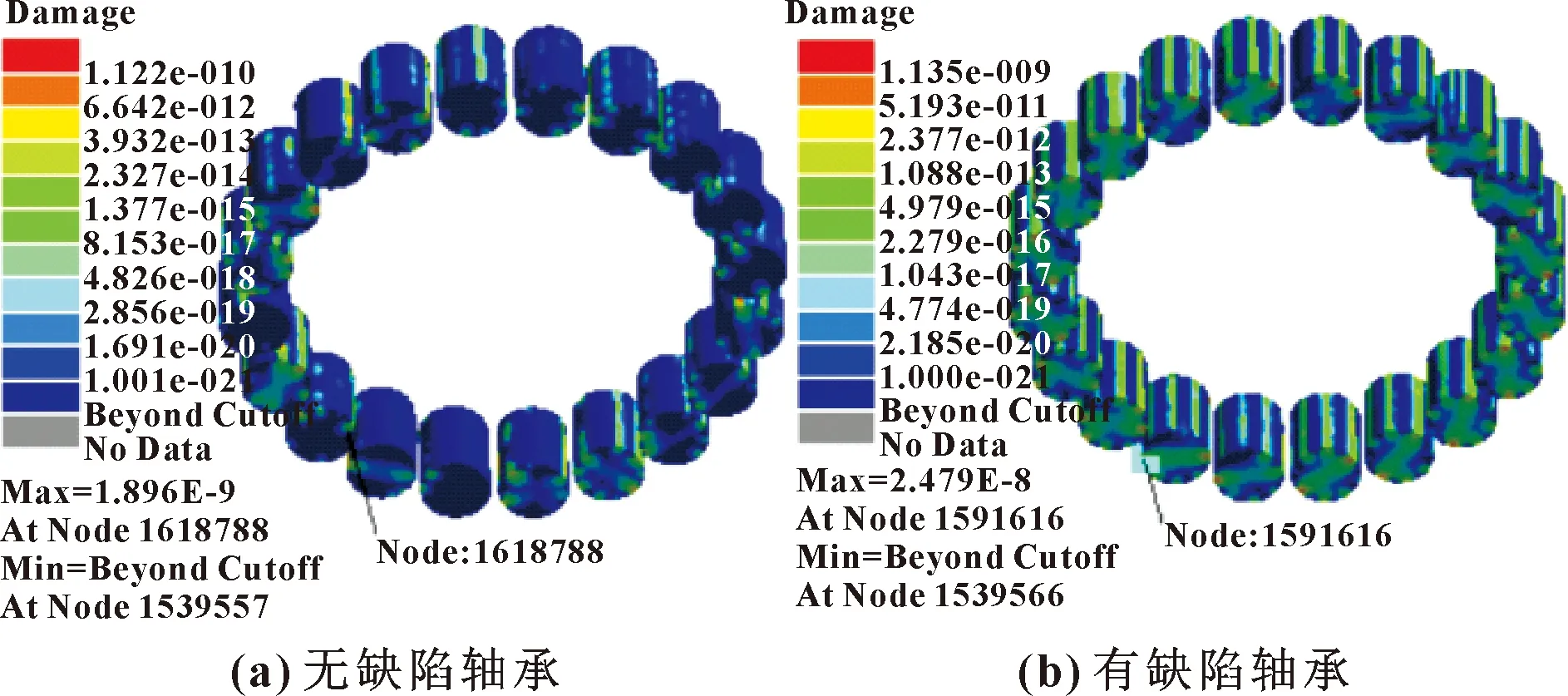
圖13 圓柱滾子損傷云圖

由圖13、圖14可知：無缺陷軸承的圓柱滾子在節點N1618788處發生損傷，其最大損傷為1.896×10，在該節點處最小壽命為5.274×10次，而多數損傷在4.826×10～2.327×10，與之對應的疲勞壽命為2.072×10～4.297×10次；有缺陷軸承的圓柱滾子在節點N1591616處發生損傷，其最大損傷為2.479×10，在該節點處最小疲勞壽命為4.034×10次，而多數損傷在1.043×10～1.088×10，與之對應的疲勞壽命為9.587×10～9.192×10次。可知大多數損傷發生在兩軸承的圓柱滾子與內、外圈接觸面上，與動力學仿真軸承的圓柱滾子受到的等效應力集中的位置相符合，進一步可以推測出軸承失效的區域。

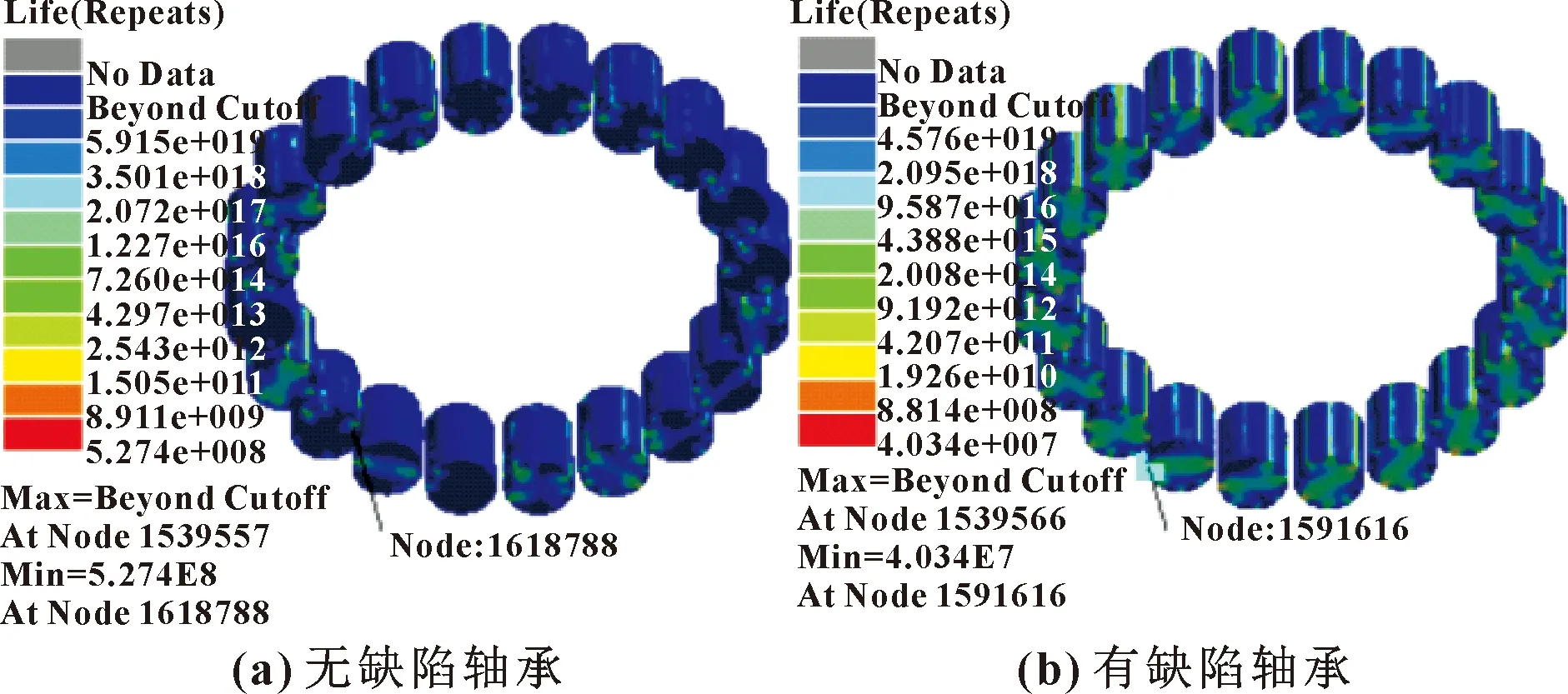
圖14 圓柱滾子壽命云圖

3.3.3 外圈疲勞分析

圖15、圖16所示分別為無缺陷軸承和有缺陷軸承外圈的損傷和疲勞壽命云圖。

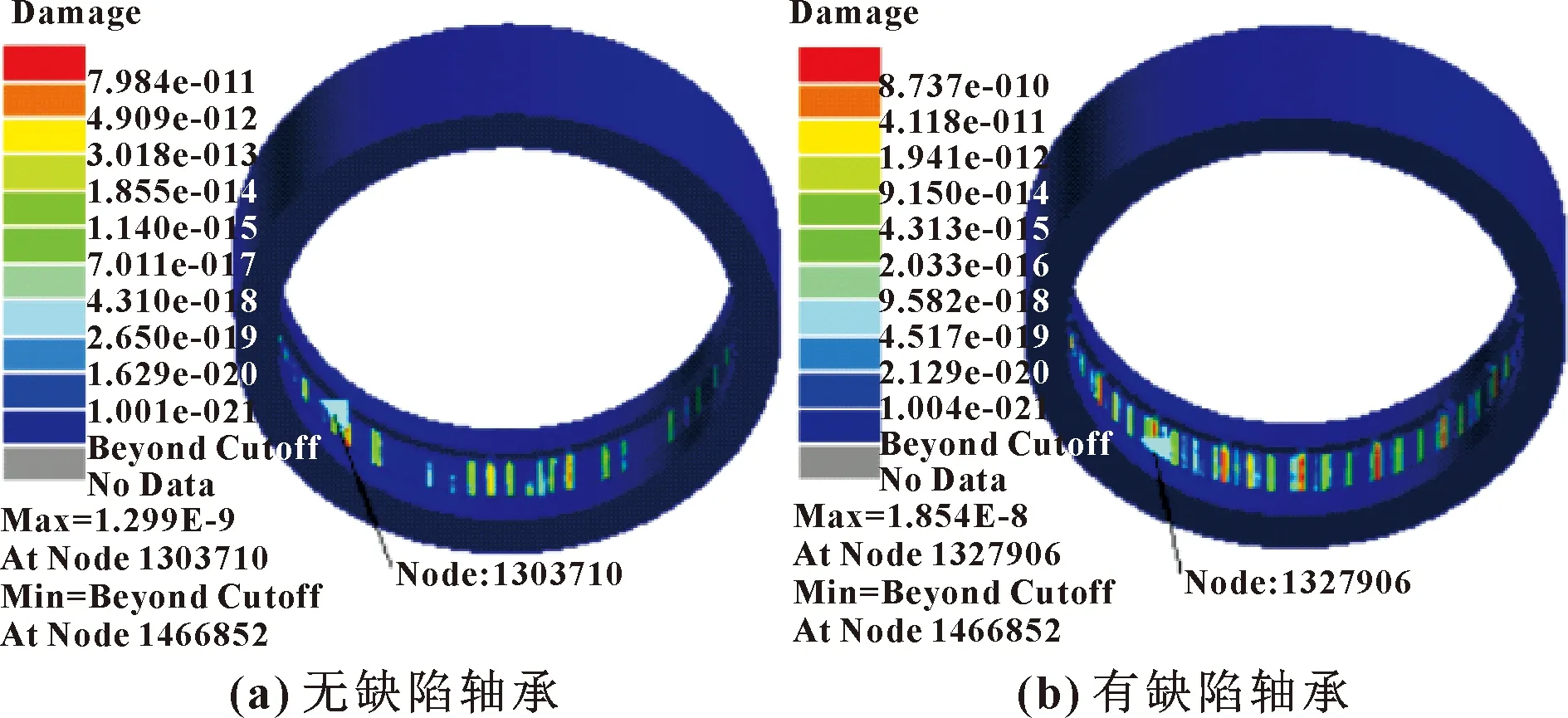
圖15 外圈損傷云圖

圖16 外圈壽命云圖

由圖15、圖16可知：無缺陷軸承的外圈節點N1303710處發生損傷，其最大損傷為1.299×10，該節點處最小壽命為7.700×10次，而多數損傷在4.310×10～1.855×10，與之對應的壽命為2.320×10～5.390×10次；有缺陷軸承的圓柱滾子在節點N1327906處發生損傷，其最大損傷為1.854×10，在該節點處最小壽命為5.395×10次，而多數損傷為9.582×10～9.150×10，與之對應的疲勞壽命為1.044×10～1.093×10次；外圈大多數損傷發生在與滾子的接觸面上，這與動力學仿真結果相符合。根據圓柱滾子和外圈疲勞分析，軸承失效發生在滾子的內、外圈滾道上。根據外圈的疲勞壽命云圖還可以看出，外圈有缺陷的軸承使用壽命比無缺陷軸承的壽命小。

3.3.4 不同轉速時軸承壽命分析

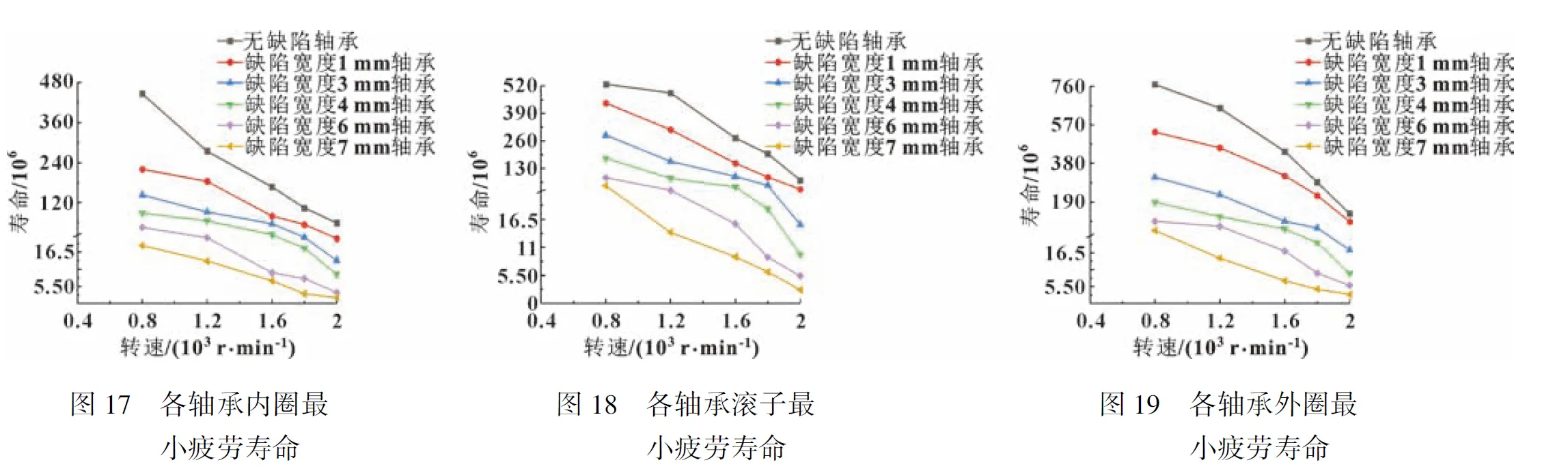
基于所建立的不同局部剝落缺陷軸承的模型，分別進行動力學仿真疲勞、壽命計算，得到各軸承部件在不同轉速下的疲勞壽命，分別如圖17—圖19所示。可知：隨著轉速增加，各軸承部件的疲勞壽命逐漸下降；隨外圈局部缺陷尺寸不斷增加，軸承各部件疲勞壽命呈下降趨勢。

4 總結

對有局部剝落缺陷軸承和無缺陷軸承進行顯式動力學和疲勞壽命分析，得出以下結論：

(1)無缺陷軸承滾子節點應力波動較小，而有局部剝落缺陷軸承滾子經過外圈缺陷時，與外圈缺陷邊緣接觸，節點應力會有劇烈的波動；

(2)轉速不斷增加時，兩類軸承各部件的等效應力均呈上升趨勢，有缺陷軸承各部件的等效應力均比無缺陷軸承的等效應力大，隨著缺陷尺寸不斷增加，缺陷軸承各部件的等效應力也逐漸增大，從而縮短了疲勞壽命；

(3)在相同轉速時，無缺陷軸承的各部件壽命均比有局部剝落缺陷軸承長；轉速不斷增加時，兩種軸承的各部件疲勞壽命均呈不同程度的下降趨勢；由于外圈存在局部剝落缺陷，隨缺陷尺寸不斷增加，外圈疲勞壽命急劇下降。