基于SCADA數據協整分析的風力發電機狀態監測

張超，趙廣翰

(內蒙古科技大學機械工程學院，內蒙古包頭 014010)

0 前言

風力發電機是進行風能發電的核心設備，由于風電場一般都位于環境復雜的地區，發電機在運行過程中受環境影響較大，一旦發生故障，將會造成嚴重的經濟損失。因此開展風力發電機組的運行狀態監測尤為重要，能夠及時發現機組運行過程中存在的故障隱患。現有的狀態監測方法是通過對機械參數進行監測來實現的，其中應用較為廣泛的參數是溫度、油液等。SCADA(Supervisory Control and Data Acquisition)系統，即數據采集與監視控制系統，在風力發電領域擔任著重要工作，監控著風速、轉速、溫度、電能、功率等。通過對這些數據的分析，可以對風機的運行狀態進行實時的監測與狀態評估。但由于風機所處的工作環境復雜，受環境及風機本身運行的影響，使得風機SCADA數據分析結果可靠性不足，無法準確地從SCADA系統采集的數據中發現故障參數，最終將導致風電場無法有效掌握風機的運營水平和健康狀態。因此需要尋求一種能夠準確分析SCADA數據的方法，實現風力發電機的狀態監測。

協整理論起源于計量經濟學，20世紀80年代初, Engle和Granger為了分析非平穩經濟變量之間的關系所提出的。這是處理非平穩時間序列長期均衡關系的一種有效的統計方法。現今協整理論也在工程領域得到應用。工程領域的被測信號一般都具有長期的非平穩性，這些信號之間可能會存在長期動態平衡關系，而協整理論正好可以用來描述工程系統中的非平穩隨機過程之間的長期動態協調關系。

本文作者在數據趨勢分析和過程監測的基礎上，提出一種基于協整分析的風力發電機狀態監測新方法。采用向量回歸方法，對多個參數進行分析，通過協整計算快速去除數據中的非線性趨勢產生殘差，用SCADA數據協整分析得到的協整殘差是否平穩來說明風機運行狀態。該方法實現了從單一過程參數分析到大量過程參數的自動解釋和分析的過渡。與其他常用的數據處理技術如神經網絡算法相比，該方法具有實現簡單、計算量小等優點。

1 協整理論

1.1 自回歸模型

自回歸(Auto Regression,AR)模型是隨機過程時間序列分析中最為基礎也是廣泛使用的一種模型，它描述序列{}在某一時刻和前個時刻序列之間的線性關系，表示為

=-1+-2+…+-+

(1)

其中：隨機序列{}是白噪聲序列，且序列{}和序列{}(<)不相關，稱模型(1)為階自回歸模型，記為AR()。

1.2 平穩與非平穩

對于隨機變量，如果其概率分布函數任意時刻都相同，不隨時間變化，即

()=(+)?

(2)

稱為平穩時間序列，反之為非平穩時間序列。

1.3 單整

在工程問題中，數據多數是非平穩的時間序列，往往不能達到平穩的要求，需要將非平穩序列轉化為平穩時間序列。單整定義：如果一個非平穩時間序列{}在階差分后變為平穩的、可逆的平穩時間序列，而該序列-1階差分后仍是非平穩的，則稱該序列具有階單整性，記為～()。因此，(0)可表示平穩序列，(1) 表示為一階單整，一般在工程問題中，單整階數≤2。

1.4 協整

協整描述工程系統的長期均衡關系。它描述了兩個或者多個非平穩時間序列的均衡關系，雖然每個時間序列的均值、方差或協方差等隨時間變化，但這些序列的某些線性組合(均衡關系)的矩在某些時刻具有不變性。

1.4.1 兩變量協整檢驗-EG兩步法

在時間序列只有兩個變量的情況下，只可能存在一個線性關系。當時間序列{}={(1,2)}中存在唯一協整關系時，EG兩步法是非常有效的，具體步驟為：

(1)用普通最小二乘回歸法估計下列方程：

1=+2+

(3)

其中：1與2為(1)的非平穩序列，則：

=1-2+

(4)

(2)運用ADF檢驗對進行單位根檢驗。如果為平穩時間序列，則1和1協整。

1.4.2 Johansen協整方法

Johansen協整檢驗是一種針對多變量的協整檢驗方法，它基于多變量的非穩態的VAR模型上，檢驗前建立VAR模型，它的數學表達式為

=-1+-2+…+-++=1,2,…,

(5)

其中：為截距；為白噪聲；為×參數矩陣，=[,,…,]，-1=[,,…,-1]，…，-=[1-,2-,…,-]，為×1維非平穩(1)向量。為滯后項。另外，協整關系可推廣至重協整：

(6)

得到殘差作為狀態監測模型。

2 實驗分析

2.1 實驗數據

實驗選用風力發電機正常工作時的最大風速、最大理論有功功率與最大實際有功功率(見圖1)來進行協整分析，采用包頭金杰公司1.5 MW雙饋風力發電機SCADA數據進行協整計算。

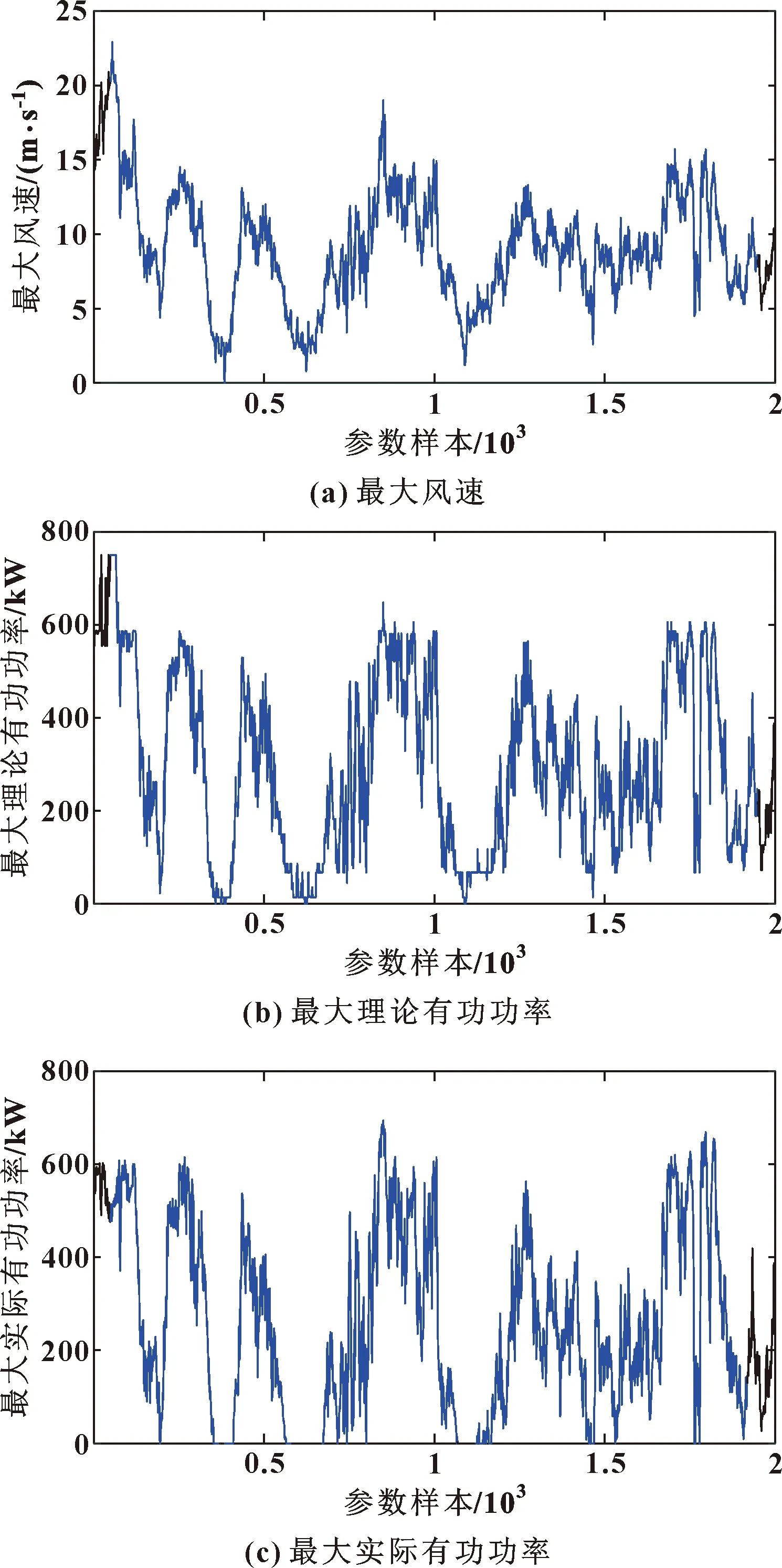
圖1 風力發電機SCADA數據

2.2 建立協整模型

利用所述方法，針對圖1數據建立協整模型，令1、2、3分別為最大風速、最大理論有功功率與最大實際有功功率。首先對所選數據進行一階差分，再對原數據與一階差分后的數據進行ADF檢驗，檢驗結果如表1所示。

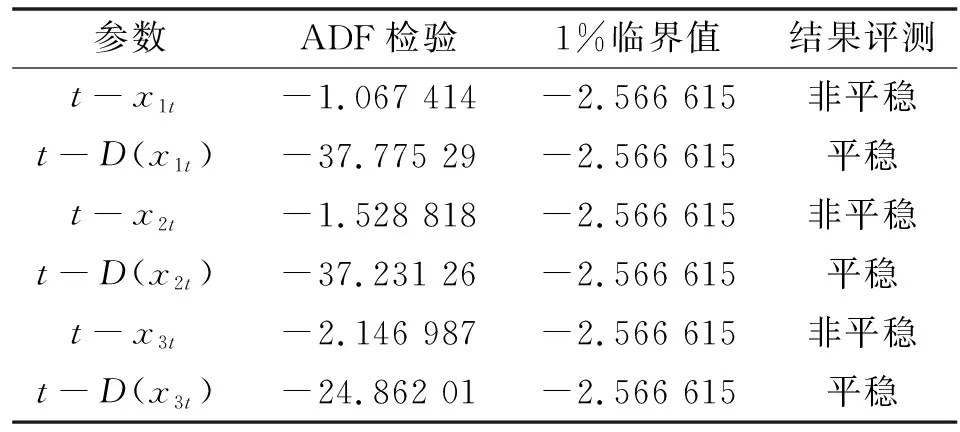
表1 ADF檢驗結果

表1中ADF檢驗值小于臨界值時，說明時間序列是平穩序列，大于臨界值時，說明時間序列為非平穩序列。從表中結果來看理論輸出功率與電機發電量經過一階差分后均為平穩變量，這符合單整定義，可以繼續進行協整分析。用上述風機數據與普通最小二乘回歸法估計方程(5)，建立協整模型：

=37174 01-1773 42+3-72518 6

(7)

由上述實驗數據與協整模型[式(7)]求標準差=80.06。對該殘差進行ADF檢驗，若檢驗結果為平穩時間序列，說明理論有功功率與電機發電量所建立的協整模型存在協整關系，若為非平穩序列說明模型建立失敗，變量間不存在協整。對殘差進行ADF檢驗，表2為檢驗結果。

表2 ADF檢驗結果

表2中，殘差經過ADF檢驗后的值小于臨界值，表明殘差為平穩時間序列，滿足協整條件，模型可用來進行風力發電機狀態檢測。圖2為風力發電機健康狀態下殘差序列。

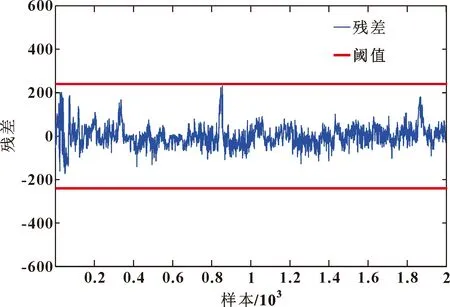
圖2 健康狀態下協整殘差

根據殘差分布特性，將標準差作為閾值，圖中閾值為(-3，3)，根據殘差是否超出閾值范圍來判斷風力發電機狀態情況。

2.3 對協整模型進行驗證

取同一臺風機故障運行狀態下的SCADA數據對式(7)表示的模型進行驗證，所采用數據如圖3所示。

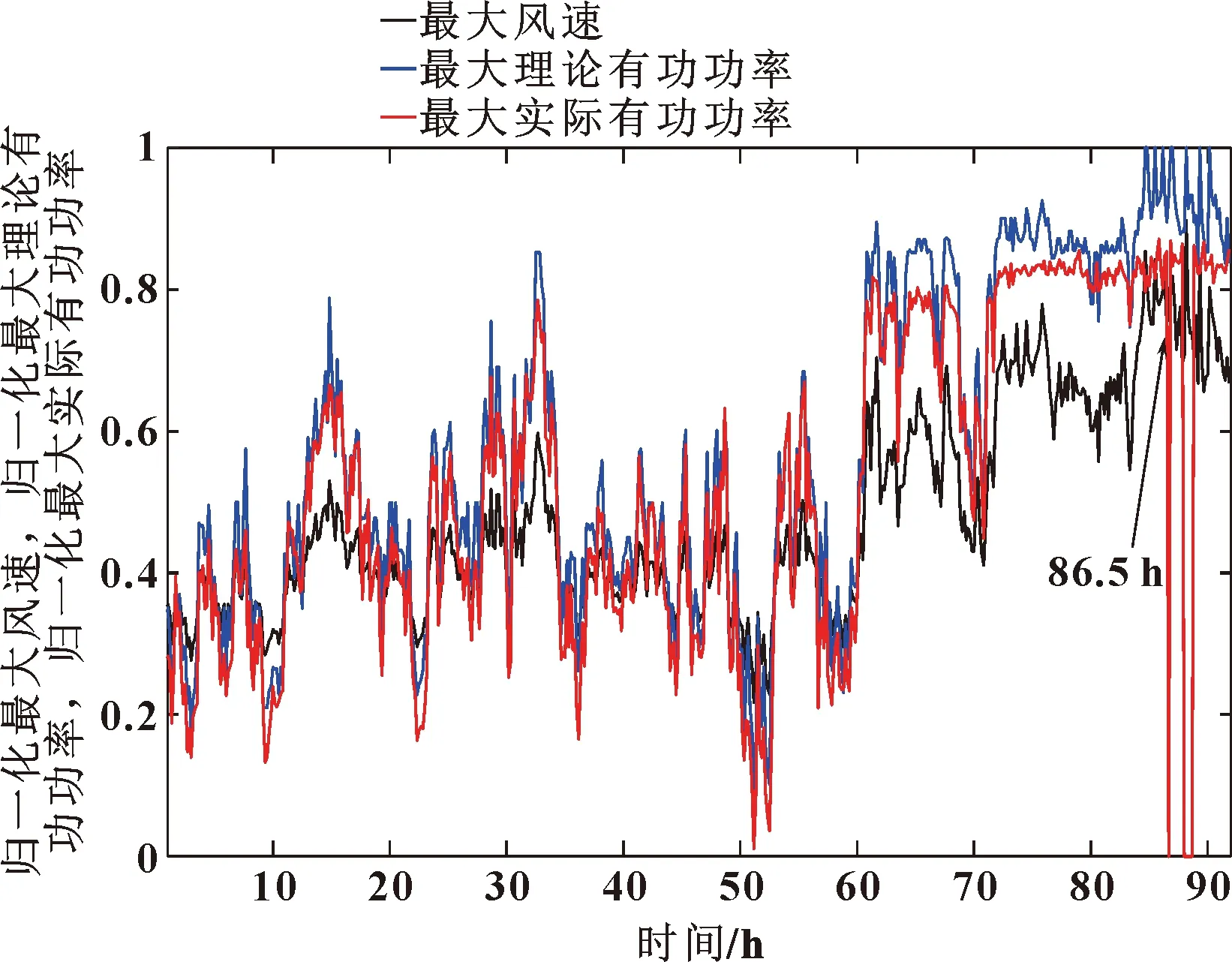
圖3 風機故障狀態下的SCADA數據

圖3中，在第86.5 h處風力發電機產生電器故障，風速與理論有功功率保持穩定時，實際輸出功率在86.5 h處出現異常驟降現象，10 min后發電機輸出功率降為0，SCADA系統發出警報，進入停機狀態。利用協整模型計算同時段協整殘差如圖4所示。

圖4 故障狀態下SCADA數據協整殘差

圖4中協整殘差在85.8 h處偏離平穩狀態呈下降趨勢，86 h處超出設定的閾值，表明風力發電機發生異常運行，停機檢查。與SCADA系統監測相比提前約40 min監測到風力發電機異常運行狀態。為了進一步對殘差模型準確性進行驗證，取包頭市1.5 MW雙饋風力發電機運行1 147 h的SCADA數據對模型進行驗證，將數據代入協整模型[式(7)]，得到殘差圖5，圖6為風機故障發生時間。

圖6中共發生18次故障停機，圖5中殘差超出設定閾值15次，均準確監測出風力發電機異常運行狀態，其中第163.3、732.5、1 063 h殘差未超出設定閾值。經反復試驗，得出原因：用于建立協整模型的SCADA數據缺少過程參數，導致出現3次協整殘差未能偏離平穩狀態，超出設定閾值。

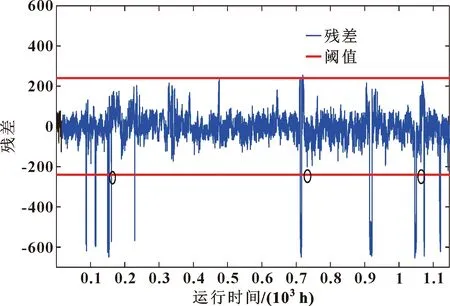
圖5 SCADA數據協整殘差

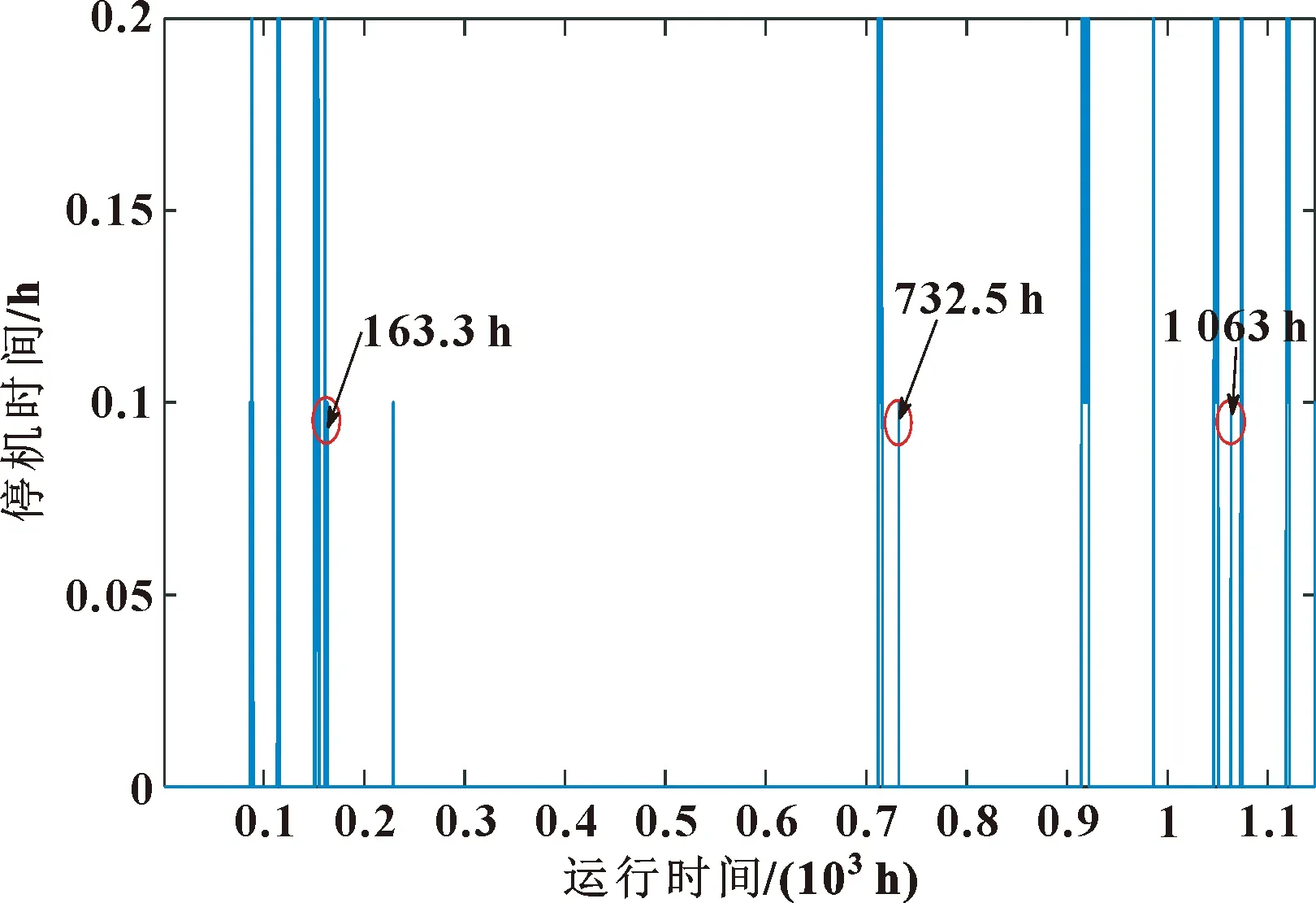
圖6 風機故障發生時間

2.4 協整分析參數優化選取

風力發電機通過葉片捕捉風能，將其轉化為機械能，并通過傳動系統進行傳輸，最后通過發電機將其轉換為電能。齒輪箱作為傳動系統重要的組成部件，對風力發電機正常運行有著重要作用，因此選取風機SCADA數據齒輪箱溫度、發電機轉速作為過程參數與平均風速、平均理論有功功率、平均實際有功功率構成5組數據建立協整模型，如圖7所示。

令1、2、3、4、5分別為平均風速、理論有功功率、實際有功功率、齒輪油箱溫度、齒輪發電機轉數，重復第2.2節步驟針對圖7中 SCADA數據建立協整模型：

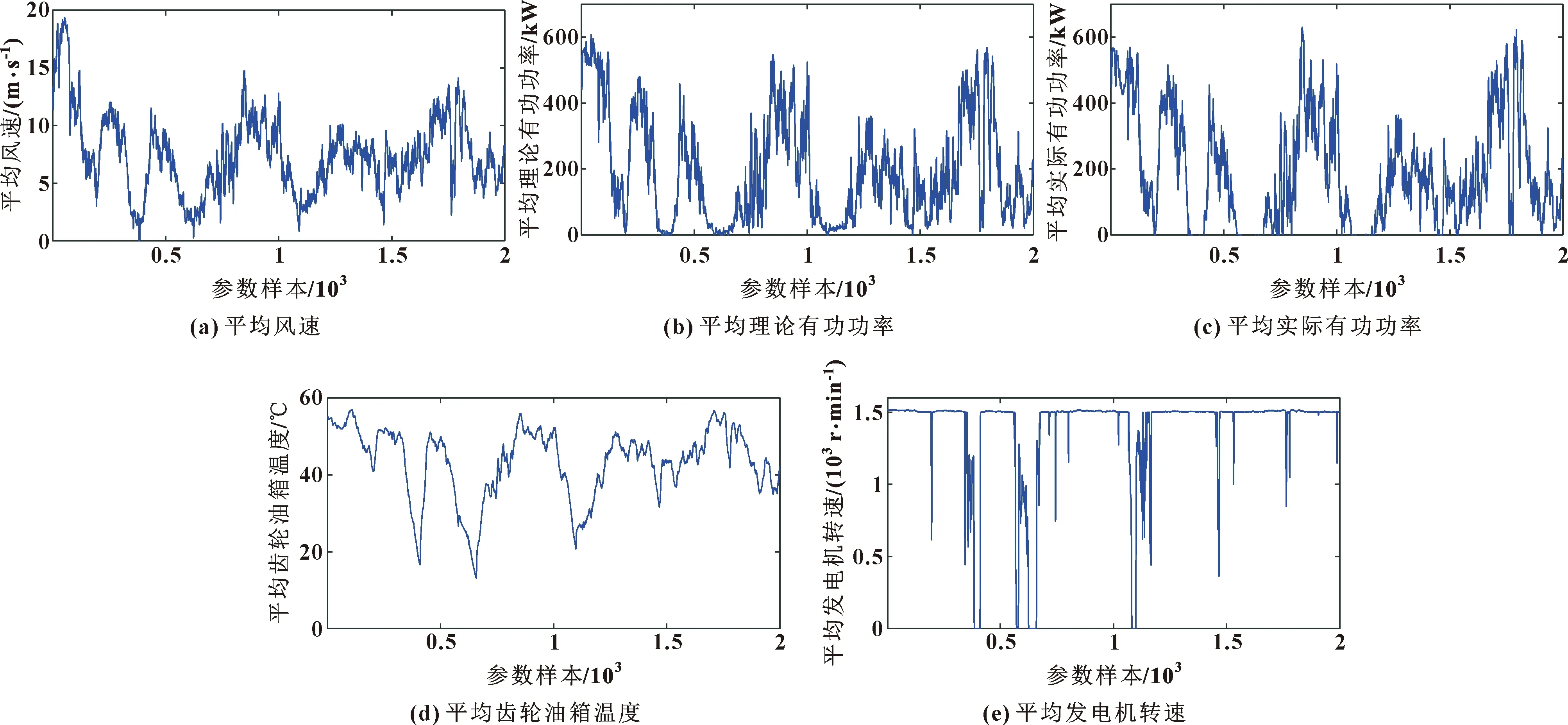
圖7 風力發電機SCADA數據

=8675 01-0811 5402+3-9808 8454+0155 7165+111339 0

(8)

對進行ADF檢驗，檢驗值為-23.237 542，小于1%臨界值-2.566 617，評測結果為平穩，數據之間存在協整關系，可用于風力發電機狀態監測。求標準差=3.21，設定殘差閾值為(-3，3)。

2.5 異常狀態識別

將上文包頭市1.5 MW雙饋風力發電機SCADA數據輸入模型[式(8)]進行驗證，得到殘差如圖8所示。

圖8中殘差超出設定閾值18次，表明發生18次故障停機，其中163.1、732.3、1 063 h處均超出設定閾值，與圖6中故障停機相吻合。所提方法可實現對風力發電機狀態進行監測。

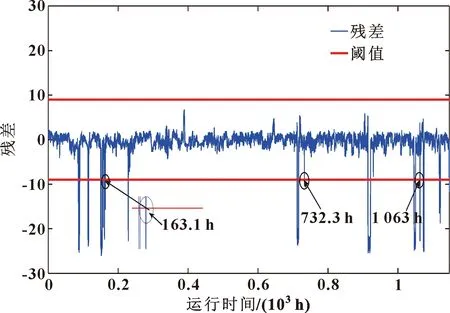
圖8 優化后SCADA數據協整殘差

3 結束語

提出一種基于風力發電機SCADA數據協整分析的風力發電機狀態監測方法，利用風力發電機SCADA數據協整過程計算出殘差模型，再調整SCADA數據參數，并用一臺已知的1.5 MW雙饋風力發電機故障數據對殘差模型進行測試。結果表明:該方法可有效通過殘差的偏離程度對風力發電機運行狀態是否異常進行監測。通過調整SCADA參數，提高了對故障判別的準確度。與其他常用的數據處理技術和神經網絡算法相比，該方法具有實現簡單和成本低的優點。