以小見大 聚焦變化 指向素養
——以一道“函數探究題”的改編為例*

周 煉

(江蘇省泰州市第二中學附屬初中 225399)

2022年4月7日，江蘇省泰州市教育局教學研究室舉辦了全市初中數學教師命題比賽

.

此次比賽以提升初三數學教師命題能力、推進初中數學命題改革、更好落實雙減政策以及新高考下教學模式的轉變為主要目的，同時也激發了全市初中數學教師以及教研員的命題熱情

.

比賽分兩種模式：改編試題與原創試題

.

筆者選擇了改編試題中的一道函數題作為初始素材，借助于幾何畫板等工具，從結構優化、問題設計、思想升華等方面對試題展開了深入研究，并在改編過程中形成了一些主張與想法，下文作具體闡述

.

1 試題原型與改編

1

.

1 試題原型

在平面直角坐標系

xOy

中，拋物線

y

=

x

-4

x

+3與

x

軸相交于點

A

，

B

(點

A

在點

B

的左側)，與

y

軸相交于點

C.

(1)求直線

BC

的表達式

.

(2)垂直于

y

軸的直線

l

與拋物線相交于點

P

(

x

，

y

)，

Q

(

x

，

y

)，與直線

BC

交于點

N

(

x

，

y

)

.

若

x

<

x

<

x

，結合函數圖象，求

x

+

x

+

x

的取值范圍

.

1

.

2 改編呈現

在平面直角坐標系中

xOy

中，拋物線

y

=

a

(

x

-

m

)(

x

-

n

)(

a

<0，

m

<

n

)與

x

軸交于點

A

，

B

(點

A

在點

B

的左側)，與

y

軸相交于點

C.

直線

y

=

c

與拋物線相交于

P

(

x

，

y

)，

Q

(

x

，

y

)兩點(

P

與

Q

不重合)，與直線

BC

交于點

N

(

x

，

y

)

.

(1)設

a

=-1，

m

=1，

n

=3

.

①求線段

AB

的長；②證明：當

c

<1時，一定存在不重合的

P

，

Q

兩點且

x

+

x

的值不會隨著

c

的變化而變化

.

(2)令

c

=

m

，且點

A

在直線

BC

的上方

.

①求

m

的取值范圍；②一定存在一個

a

的值，對于任何符合的

m

,

n

均可以使得

x

+

x

-

x

為常數，求

a

的值以及

h

的取值范圍

.

2 改編策略

2

.

1 以小見大的維度延伸

·將參數一般化，以拓寬試題的內容

一道試題的背后，往往是命題者對試題所涉及的方方面面進行透徹研究的結果，但考慮到學生的思維水平與接受程度，一般都會對結論作特殊化處理，以更加具體的問題情境作為呈現載體

.

但在改編一道試題時，若依舊停留在特殊化階段，命題的視野與格局便無法打開，看到的也僅僅是特定條件下的固化結論，不具備遷移性與推廣性，更談不上創新與發散

.

若想要激蕩出更多的靈感就要先將試題一般化，對于函數題來說主要是將參數一般化，這是一個由點到面再由面到點的過程，只有經歷了這樣的過程，才會形成更豐富、寬廣、多元化的良好命題樣態

.

本題函數原型是一個完全確定的二次函數，但若囿于某個具體的函數表達式，改編的范圍便會十分狹隘，延伸面也較小

.

為了創造出更多的可能性，勢必要將拋物線

y

=

x

-4

x

+3推廣為更一般的形式

.

經分析，發現該函數在整個問題中與

x

軸的兩個交點密切相關，所以將其一般化為交點式

y

=

a

(

x

-

m

)(

x

-

n

)是比較合理的，這樣便能在緊扣原型的基礎上以小見大地切入

.

至于原型中的直線，在改編時一開始給出的是一般形式

y

=

c

，但由于后續要研究更具體的存在性問題，在多次嘗試后發現令

y

=

m

能與

y

=

a

(

x

-

m

)(

x

-

n

)產生更為具體的、個性化的代數關聯，最終確定“

a

，

m

，

n

”為本題的參數設定

.

·將結構層次化以促進思維的遞進

試題改編不同于直接命題，因為試題原型本身是有研究基礎的、是原命題者思維的結晶，所以相當于站在“巨人的肩膀”上再研究、再發現

.

試題改編雖要立足并尊重原型，但更要高于并突破原型，要能在已有研究成果之上彰顯創造性

.

而正是這樣逐漸往高處走的趨勢，反而有可能會在改編后變得“不接地氣”，甚至與學生的思維水平出現斷層

.

為了避免這樣的狀況發生，當改編后的問題比較抽象或思維過于密集時，可以為其設置有層次的遞進結構，通過從特殊到一般的引導，給學生創造一個小的切口，再從這個切口出發以小見大、循序漸進地展開研究

.

本題改編共有三處在結構層次化以促進思維遞進方面作了較為周密的思考

.

例如在(1)①中設計“計算線段

AB

的長”這一問題，是因為在(2)①中要求

m

的范圍需要先算點

A

，

B

，

C

的坐標，而后者在引入參數后對運算的要求更高，有了①的鋪墊，學生對于

A

(

m

，0)，

B

(

n

，0)，

C

(0，

amn

)，

y

=-

amx

+

amn

這樣含參數的坐標與函數表達式的接受度會更高，在運算時也就有跡可循

.

同樣地，還有(1)②中設計“證明當

c

<1時，一定存在不重合的

P

，

Q

兩點”這一問題，是希望學生能關注到直線與二次函數圖象不是一直存在交點的，會受到一些參數范圍的限制，而這樣的認識對于(2)②中“一定存在一個

a

的值，對于任何符合的

m

，

n

”這一條件的理解會更加深刻，從而聯想到這一范圍可能與

x

，

x

的存在性相關

.

最后，在(1)②中設計“證明

x

+

x

的值不會隨著

c

的變化而變化”這一問題，依舊是為(2)②中探究“

x

+

x

-

x

”是否為定值埋下了伏筆，引導學生將簡單情境中得出的

x

+

x

的性質自主遷移到最后一問中去

.

像這樣逐層遞進、從特殊到一般的良好試題結構可以引導學生進行類比，以此激發出更多的聯想，能沿著一條清晰的思維鏈條逐漸向上攀登

.

2

.

2 聚焦變化的改編理念

變化是一切事物的本質特征，或者說這個世界上唯一不變的就是變化

.

在問題改編的過程中賦予變化視角，往往能看到事物的多面性

.

但雜亂無章的變化是沒有研究價值的，一般來說，不變性與存在性是在變化情境中研究問題的兩個常見維度，以此重新審視問題往往會獲取不一樣的探究視角

.

本題改編原型的第二問就蘊涵著豐富的變化因素，例如在動直線平移的過程中找到符合

x

<

x

<

x

的圖象位置，這是一種變化中的存在性；發現

x

+

x

+

x

中的

x

+

x

不會隨著直線位置的變化而變化，這又體現出了一種變化中的不變性

.

作為改編，雖然不能完全照搬原問題的設計，但其背后的思想、方法是可以延續甚至升華的

.

聚焦變化既是對原型的一種繼承與發揚，同時也是以多樣化視角尋求改編新意的重要契機

.

·變化中的不變性

原型中關于變化中的不變性是相對隱蔽的，再加上題目中并沒有直接給出研究不變性所需的參數，對于代數意識較弱的學生可能會出現入門障礙

.

另一方面，設出參數后的推理過程相對簡單，也不能充分體現學生的代數素養

.

基于此，決定在原型基礎上在兩處分別降低、提升一個維度對變化中的不變性進行改編

.

第一處：在(1)②中通過引入變量

c

，構建了無論

c

取何值，都不影響

x

+

x

恒為定值的結構設計

.

對比原型來看，將“垂直于

y

軸的直線

l

”具體化為函數表達式

y

=

c

，這實質上是多鋪設了一層臺階，幫助學生搭建了設參數描述函數交點的腳手架，避免了在原型中由于缺乏參數意識造成一部分學生在一開始就陷入無從下手的“恐慌”局面

.

學生在得到拋物線表達式

y

=-

x

+4

x

-3后，只要令-

x

+4

x

-3=

c

，再根據

c

<1便可得

Δ

=4(1-

c

)>0，從而發現一定存在不重合的

P

與

Q

兩點

.

第二處：在(2)②中將原型中垂直于

y

軸的直線

l

設定為

y

=

m

后，發現當

a

取任意值時，與之間沒有必然的數量關系(如圖1、圖2)，但是將

a

取為-1后，無論怎樣改變

m

與

n

的值，一直存在著不變的數量關系(如圖3、圖4)

.

利用這樣的關系構造為

M

·

x

模型便可以將其設計為任意中的確定問題，其中

M

代表了題目中的所有變量，而

x

則是關于要確定位置的常量的代數式，一般來說將變量提取后，令后面含常量的代數式的值為0，即可讓變量消失，從而讓變量的變化不影響整體的取值，以達到變化中不變的效果

.

具體地，令

y

=

m

可得

ax

-

a

(

m

+

n

)

x

+

amn

-

m

=0，解得

x

+

x

=

m

+

n.

再令-

amx

+

amn

=

m

，又可以解得從而因為存在一個

a

的值使得

x

+

x

-

x

為常數，所以在中令即

a

=-1，此時

x

+

x

-

x

與

m

無關，為常數0

.

這與原型中的問題有所區別的是，它需要滿足某個特定的前提條件，要找到某個特殊位置才能讓某個量不會隨著變量的變化而變化，這在原型思維層級的基礎上又多了一層探究性與不確定性，對學生的能力要求自然也就更高

.

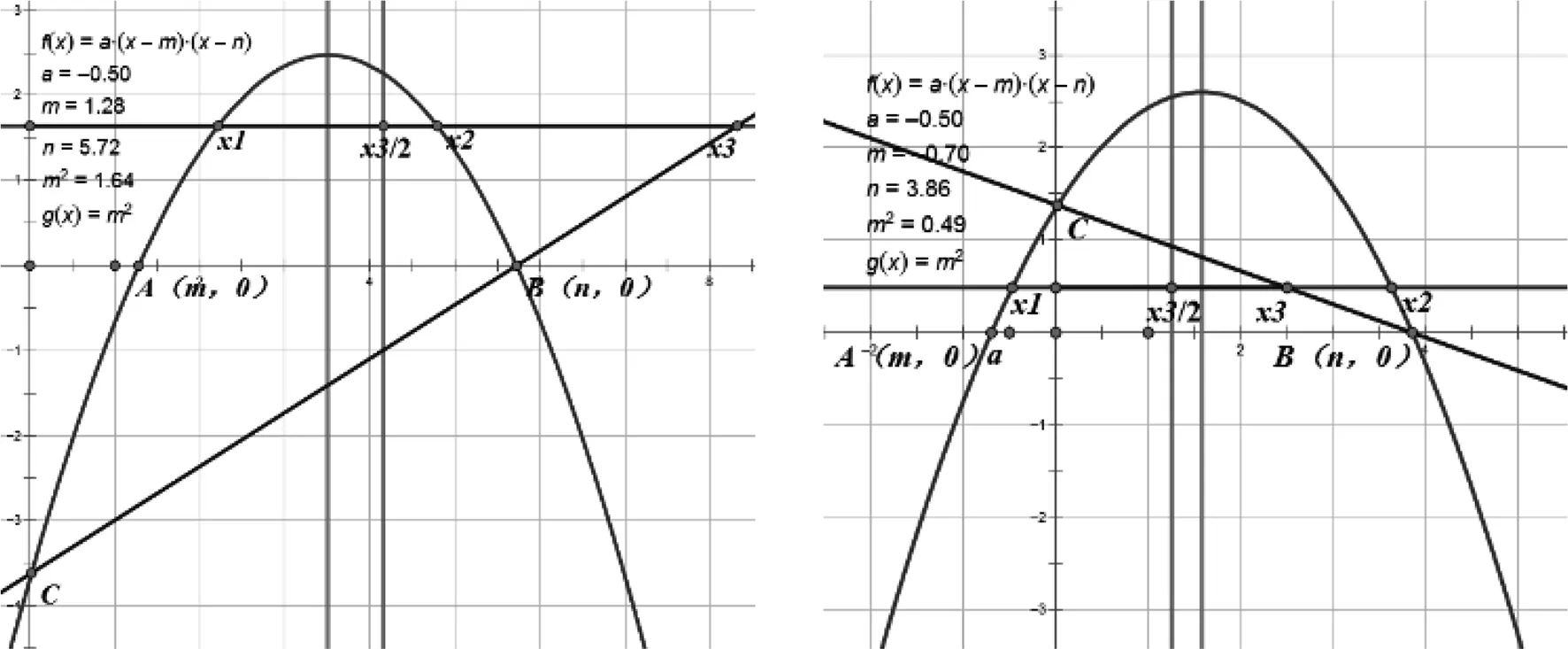
圖1 圖2

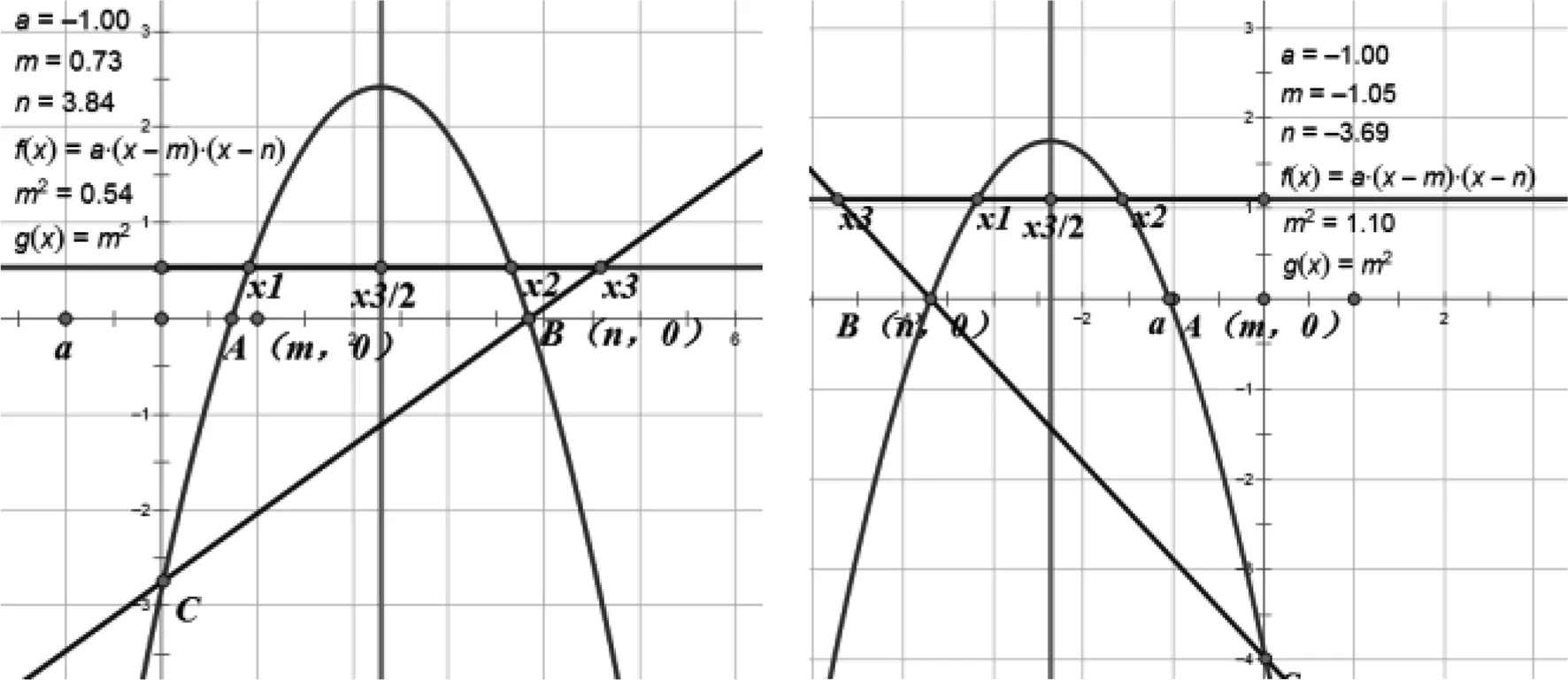
圖3 圖4

·變化中的存在性

由于重新設定的問題背景融入了大量參數，所以函數圖象相較于原型結構固化的缺陷，有了更加自由的延伸與探索空間

.

在改編時可以對不同的參數賦值，通過觀察、分析、推算、驗證等方法以發現更多變化中的存在性，并將其設定為范圍求值、證明等問題，從而將試題改編再推上一個新的高度

.

本題共有兩處改編體現了變化中的存在性

.

圖5

第一處：在(2)①中“已知點

A

在直線

BC

的上方，求

m

的取值范圍”正是基于原型中“求直線

BC

的表達式”、指向存在性研究的改編

.

在改編時，借助于幾何畫板對不同的參數賦值使圖象位置發生變化，發現在變化的過程中點

A

時而落在直線

BC

的下方(如圖5、圖6)，時而落在直線

BC

的上方(如圖7)，并且無論怎樣改變

n

值的大小，都不影響點

A

與直線

BC

的位置關系，唯獨當

m

分別為正值與負值時，才會產生兩種不同的位置狀態

.

本題以點

A

在直線

BC

的下方作為要滿足的存在性要求對原型進行了改編，發現通過代數推理可得0>-

am

+

amn

，因為

a

<0，所以

m

<

mn.

解這個不等式需要分類討論：如果

m

<0，那么

m

>

n

，但這與條件中的

m

<

n

矛盾，不符合題意需要舍去；如果

m

>0，那么

m

<

n

，符合題意

.

圖6 圖7

第二處：在(2)②中“

x

+

x

-

x

為常數”討論的前提是“對于任何符合的

m

與

n

”均成立的任意性，而原型中關于“

x

<

x

<

x

”并未提出相關參數使問題恒成立的范圍要求，但

x

與

x

一定存在嗎？在對原型進行改編時尤其側重了對這一現象的研究

.

在用幾何畫板繪圖時發現

x

必然存在，但當直線位于拋物線頂點上方時是不存在

x

與

x

的(如圖8、圖9)

.

此時設定條件“一定存在一個

a

的值”是為了控制直線

y

=

m

與拋物線圖象必須存在交點

.

從代數角度看，也就是聯列兩個函數表達式后根的判別式要大于0，即在

x

-(

m

+

n

)

x

+

mn

+

m

=0中，

Δ

=(

n

-3

m

)(

m

+

n

)>0

.

對于該不等式的討論一般要分同正或同負兩種情況，略微繁瑣，但若直接給出其中一項的正負性又會讓題目缺乏層次感，過于淺顯

.

在秉持著簡約命題理念的同時又希望能蘊含較為豐富的推理內容與素養成分，最終決定給出條件其中

h

為可以任意賦值的常數；只要選擇合適的

h

的范圍，就可以使交點一直存在

.

具體地，因為所以

n

與

m

同號，由①可知

m

>0，那么

n

>0，

m

+

n

>0，所以

n

-3

m

>0，即要在時結論一定成立，便有

h

≥3

.

正是

h

這樣一個新參數的引入讓本題煥發出了新的生命力，在常數與變量、恒成立與存在性的差異與統一中使得問題的代數意蘊更加濃厚，指向了更高階的代數素養

.

圖8 圖9

3 素養表現

3

.

1 扎實的運算功底

參數引入是本次改編的一大特點，除了第一問的題①是解簡單的一元二次方程，后面三個問題均涉及一定量的參數，而在參數較多的情況下能根據法則和運算律進行正確運算，是代數素養達成的一種高度體現

.

相較于小學階段更加注重式的研究，初中階段更關注學生的抽象思維能力，在腳手架搭建合理的情況下適當設置一些參數，可以反映出學生能否選擇合理的運算策略以解決結構不良的代數問題，并以此促進學生運算素養的發展，這也有助于形成規范化思考問題的品質，養成一絲不茍、嚴謹求實的科學態度

.

3

.

2 必要的幾何直觀

改編后的問題只有第一問給出的是具體函數，但隨著解題的不斷推進，學生會愈發感受到函數的抽象性，越來越覺得無從下手，事實上這是參數增多后所引發的必然結果

.

本題之所以沒有畫出函數圖象，就是希望學生能嘗試著自己主動畫圖，通過圖象讓抽象的代數研究更加具體，以發展運用圖表描述和分析問題的意識與習慣，逐漸形成幾何直觀的數學素養

.

前面提到，改編時問題的結構設置是逐層遞進的，學生可以先從第一問中的具體函數圖象開始畫起，并以此類比畫出后面抽象函數的大致草圖建立形與數之間的聯系

.

當然，僅僅依靠圖象分析并不能完全說明問題，依舊需要借助于計算與推理進行說理

.

但構建直觀模型對于把握問題本質、明晰研究路徑等方面的優勢是不言而喻的，它能讓思維看得見、摸得著，讓推理有跡可循

.

3

.

3 嚴密的推理能力

推理能力主要是指從一些事實和命題出發，依據規則推出其他命題或結論的能力

.

本題雖然是一道代數題，但對學生的推理能力卻有相當的要求，尤其是最后一問，當學生面臨很多參數與不等式時，要將這些不等關系加以綜合、分析以形成一條清晰的推理主線，是需要非常嚴密的整合能力的

.

另外，以小見大、聚焦變化的改編方式，也讓題目中整體結構從特殊到一般的類比，關于存在性與不變性的分析、表述都建立在了邏輯性的基礎之上

.

由此看來，改編后的試題需要學生較強的推理能力

.

相信經歷了這樣的過程后，可以讓學生感悟到數學的嚴謹性，有助于培養學生重論據、合乎邏輯的思維方式，形成實事求是的科學態度與理性精神

.