G-DINA認知診斷模型族：特征、關系與新進展

楊 睿 毛秀珍 何 潔 王 霞

一、引言

認知診斷理論（cognitive diagnostic theory，CDT）是認知心理學與心理測量學相結合的產物。它根據作答反應與項目特征，運用認知診斷模型（cognitive diagnostic model,CDM）診斷被試的認知結構、加工技能和認知過程，反饋個體知識結構的優勢與不足，進而為未來學習提供個性化指導。CDT作為現代測量理論，引領著國際教育與心理測量理論及實踐發展，得到了廣泛關注與深入研究。

認知診斷可以分析連續潛在特質、診斷離散知識結構，還可以同時評估個體潛在特質和知識結構。潛在特質模型、潛在分類模型、非參數人工智能和證據中心設計是四類主要的認知診斷方法[1]。特別地，DiBello，Roussos和Stout從一般到特殊的視角系統介紹了潛在特質和潛在分類模型[2]；Fu和Li介紹了60多種潛在分類模型[3]。

模型研究是認知診斷理論的核心，近二十年來得到了極大的豐富和發展。CDM經歷了從單一測驗條件到復雜測驗條件模型、從低階到高階模型、從特殊到一般模型的發展特點。首先，項目計分方式是最基礎的測驗條件，通過考查屬性多級計分、多解題策略推動了復雜測驗條件下CDM的研究。其次，借鑒結構方程模型思想，CDM從低階潛類別模型發展到結合潛在特質與離散知識結構的高階CDM。最后，CDM從常用的決定型輸入、噪音“與”門模型（deterministic inputs,noisy“and”gate model,DINA），決定型輸入、噪音“或”門模型（deterministic input,noisy“or”gate,DINO），加性認知診斷模型（the additive CDM,A-CDM）和縮減的重參數化統一模型（reduced reparameterized unified model,RRUM）等發展到一般化認知診斷模型。Ma和de la Tore[4]總結了三類一般化診斷模型：一般化DINA模型（the generalized DINA model,G-DINA）[5]、一般診斷模型（a general diagnostic model,GDM）[6]和對數線性認知診斷模型（the log-linear cognitive model,LCDM）[7]。

一般化CDM具有一般化飽和結構，約束條件少、參數多、表達式復雜，適用范圍廣。de la Torre通過不同鏈接函數證明了DINA、DINO、A-CDM和RRUM等都是約束化G-DINA模型[5]。事實上，大部分CDM都與G-DINA模型存在直接或間接的關聯，G-DINA模型及其約束化模型幾乎涵蓋了現有的參數化認知診斷模型。通過梳理現有CDM，可將CDM分為二級評分模型及擴展的多級評分模型、結合屬性多級、多解題策略的復雜測驗條件模型以及高階認知診斷模型。以下針對不同模型的特點、關系與實踐進行評析，構建了以G-DINA模型為中心的CDM樹狀發展圖，并對認知診斷在模型發展、參數估計和實踐應用等方面的研究提出思考和建議。

二、G-DINA及其約束化CDM

（一）G-DINA模型

de la Torre將作答反應的方差分解為截距效應、項目考查屬性的主效應以及屬性之間各階交互效應之和建立了G-DINA模型[5]。該模型表達的正確作答概率P(ai)在一致性、logit和log三種鏈接函數F(·)下具有相同表達式，即：

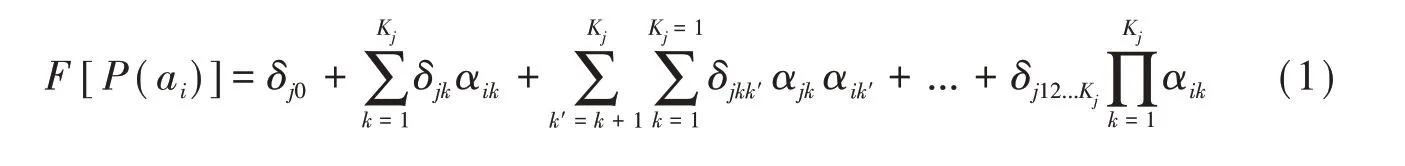
其中，δj0和δjk表示項目j的截距效應和屬性k的主效應，取值非負；δjkk'，δjkk'k''，...，δj12...Kj依次代表對應屬性之間的二階、三階到最高階交互效應，可以取任何實數。鑒于只有項目所考查屬性的子集才會影響項目作答反應，de La Torre定義了“縮減的知識狀態（α*）”，以簡化計算。G-DINA模型是飽和模型，參數較多，能區分所有α*的作答概率。它適用于語言診斷測試，并已廣泛用于國際國內英語能力的認知診斷評估[8-10]。

（二）約束化G-DINA模型

在不同約束條件下可將G-DINA模型簡化為多種常用的CDM。例如，在一致性鏈接下，若G-DINA的屬性間不存在各階交互效應，便得到A-CDM；若G-DINA模型的主效應δjk=0，同時除最高階之外的各階交互效應為0，就得到DINA模型；若G-DINA模型中屬性間效應滿足δjk=-δjkk'=δjkk'k''=就得到DINO模型；再如，在log鏈接下，若G-DINA屬性間只存在主效應而不存在任何交互效應時，就是NIDA模型。G-DINA模型與常用診斷模型的關系詳見de la Torre、高旭亮和涂冬波[5,11]。

目前，大部分模型都是適用于0-1計分項目的基礎模型，例如G-DINA、DINA、DINO、A-CDM和RRUM模型。多級評分項目廣泛存在于各類測驗，在G-DINA模型基礎上圍繞多級評分項目邁出了擴展CDM最重要的一步。

三、多級評分CDM

等級反應模型（graded response model,GRM）、稱名反應模型（nominal response model,NRM）和分部評分模型（partial credit model,PCM）是三類最常用的多級評分項目反應理論模型。CDM中，一方面借鑒GRM、PCM和NRM推廣了多步驟評分項目和稱名反應選擇題的CDM，另一方面還發展了適用于干擾項選擇題的多級評分CDM。

（一）多步驟評分CDM

1.基于GRM推廣的多級評分CDM

令項目j的最高得分為mj，GRM通過相鄰累積得分概率之差計算被試i在項目j上恰好得t（t∈{0 ,1,...,mj}）分的概率，即：P(xij=t|αi)=P*(xij≥t|αi)-P*(xij≥t+1|αi)。類似地，認知診斷

中令δjt=(δjt0,δjt1,...,δjt1,2,...,Kj*)表示得分大于等于t分對應于G-DINA模型的項目參數。那么鏈接函數F(·)下一般多級評分認知診斷模型(the general polytomous diagnosis model,GPDM)的累積概率可表示為：

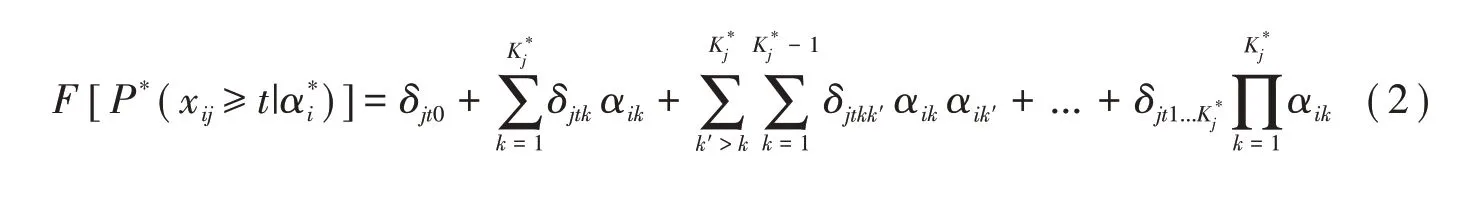
于是，GPDM的項目反應函數成為：

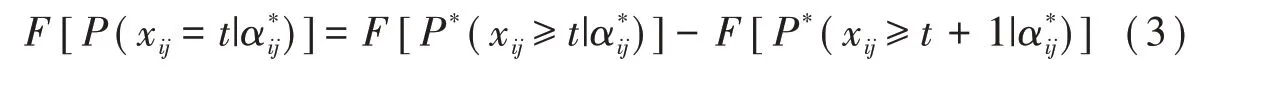
一致性鏈接中，累積概率模型（2）換成DINO或DINA模型，就得到多級評分DINO（polytomous-DINO,P-DINO）模型[12]和多級評分DINA（polytomous-DINA,P-DINA）模型[13]。

GPDM還可通過得分類別參數來定義，即：

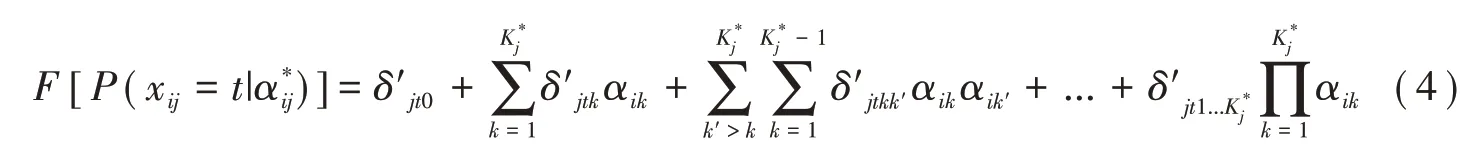
每個得分類別的項目參數是相鄰累計得分類別項目參數之差，即：

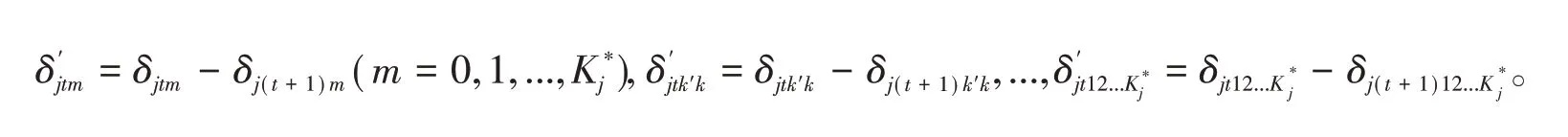
于是，多級評分項目中各個得分類別和累積得分類別q向量將變得非常重要。但GPDM、P-DINA和P-DINO均沿用傳統Q矩陣的定義，沒有細化不同得分類別所考查的屬性。

此外，蔡艷、苗瑩和涂冬波[14]指出，P-DINA和PDINO中被試往往得到極端分數，不足以反映被試間的差異。于是，他們修訂了P-DINA中的理想得分指標ηij，得到GP-DINA模型。GP-DINA在參數估計、屬性診斷率和實踐應用方面都比P-DINA模型更具優勢[15]。

2.基于PCM推廣的多級評分CDM

GRM假設項目各步驟難度單調遞增，PCM則強調正確作答項目需要完成若干步驟。PCM中第t步視作正確作答前t-1步條件下的0-1評分項目，僅與第t-1步相關，各步驟難度參數是獨立的。基于PCM推廣得到了一般化分步評分診斷模型（General Partial Credit Diagnostic Model,GPCDM）和局部或相鄰類別鏈接函數的多級評分DINA（polytomous DINA based on local or adjacent categories link Function,LC-DINA）。

前者采用logit鏈接函數的定義，將G-DINA模型作為加工函數，化簡得到如下表達式[16]：

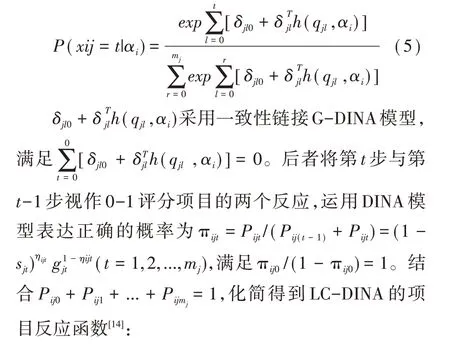
此外，與GPCDM和LC-DINA模型不同，Ma[4]和de la Torre[5]強調項目作答步驟有序，即當被試正確完成前t步，同時錯誤完成第t+1步時得t分。他們基于序列化思想運用加工函數建立序列過程CDM：

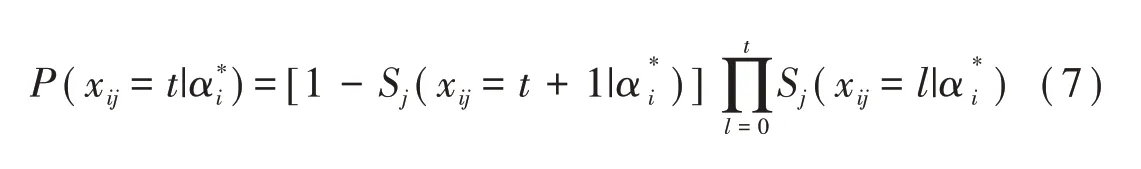
過程函數Sj(xij=t|α)表示被試正確作答第t步的概率，顯然Sj(xij=0|α)=1且Sj(xij=mj+1|α)=0。當使用G-DINA模型計算過程函數S時便得到序 列G-DINA（sequential G-DINA model，Seq-GDINA）模型。

GPCDM、LC-DINA和Seq-GDINA都將項目作答視為多個步驟，基于項目作答步驟建立起項目反應模型，也都指出得分類別q向量的重要意義，并基于得分類別定義項目參數。鑒于此，Ma[17]和de la Torre[18]提出限制性和非限制性Q矩陣；苗瑩[14]等和高旭亮[11]等沿用了限制性Q矩陣方法；苗瑩等還建議基于GRM推廣的多級評分CDM使用累加q向量[14]。此外，研究者還通過分析干擾選項的q向量提出適用于選擇題的多級評分CDM。

（二）具有干擾選項的多級評分CDM

1.多選項DINA模型（multiple-choice DINA，MC-DINA）

NRM適用于稱名類選擇題，項目得分代表對應的選項類別。Templin,Henson,Rupp,Jang和Ahmed[19]借鑒NRM思想將LCDM模型推廣到多級評分稱名反應診斷模型（Nominal Response Diagnostic Model,NRDM）。

事實上，大部分選擇題都設置了干擾選項。de la Torre[18]首次提出對干擾項（記其個數為）的q向量進行編碼，并記非干擾選項的q向量為0，稱為非編碼選項。于是，選項總數記為然后依據（T表 示 轉置）可將被試αi分到期望選項h'，不能被分到某個選項的被試組統一記gij=0。令第g(g∈{0,1,2,...,H*j})組被試選擇每個選項的概率為P（h|g），在條件下估計參數，這就是MC-DINA模型[18]。

MC-DINA模型充分挖掘了干擾項信息，對選擇題實現多級評分，具有重要意義。但其參數較多、編碼選項通常不包含所有可能的屬性模式，從而被試可能被分到多個干擾選項組，難以準確歸類分析。鑒于此，Ozaki[20]改進MC-DINA模型提出三類結構化DINA模 型（the structured DINA models）：MC-SDINA1、MC-S-DINA2和MC-S-DINA3。

2.結構化多選項DINA模型

（三）多級評分CDM簡評

多級評分項目CDM主要沿著兩條思路展開研究。一方面借鑒GRM和PCM將常用CDM推廣到多步驟計分項目，另一方面基于NRM推廣了稱名類項目多級評分CDM并提出具有干擾選項的多級評分選擇題模型。首先，GPDM、P-DINO、P-DINA和GP-DINA都基于GRM相鄰累積得分概率之差獲得了得分概率模型。基于GRM推廣的方法簡單易行，也適用于其它約束化CDM，如A-CDM、LLM和R-RUM等。其次，GPCDM和LC-DINA是在PCM基礎上推廣的多級評分CDM，將第t步視為前t-1步條件下的0-1評分項目，適用于步驟間具有依賴關系的項目。而序列G-DINA則將項目作答步驟視為獨立且有序的事件，適用于具有嚴格解題步驟的項目。再次，NRDM是基于NRM模型推廣的適用于稱名反應選項的一般化多級評分CDM。對NRDM取logit鏈接就成為參數定義在得分類別上的GPDM。最后，MC-DINA和三類MC-S-DINA模型通過分析干擾選項的特點建立了選擇題的多級評分項目，開創性地挖掘了選擇題中隱藏的被試內在反應過程，打破了“選擇題不能提供詳細作答信息”的傳統觀念。

項目計分方式是最基礎的測驗條件，也得到較為深入的研究。教育測驗、心理測量和社會調查的測驗情景紛繁復雜，如多解題策略、屬性多級記分等都是典型的項目特征。于是，建立處理復雜測驗條件的診斷模型便具有了重要意義。目前，圍繞G-DINA模型，結合多解題策略和屬性多級等項目特征擴展了多類CDM。

四、復雜測驗條件的CDM

（一）多策略CDM

令項目j有V種解題策略，被試i運用策略v的概率為P(νij-ν|αi),P(xij+1|νij=ν,αi)為被試αi運用策略v時正確作答項目的概率。它們是建構多策略CDM的核心。

1.二級評分項目多策略DINA和RRUM模型

被試可能嘗試多種策略解題，建立如下多策略CDM的一般表達式：

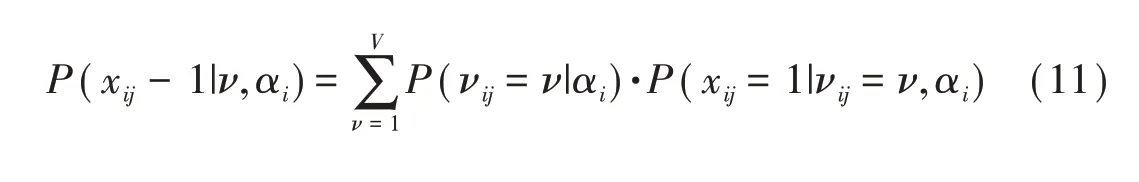
de la Torre與Douglas[21]和劉鐵川，趙玉和戴海琦[22]均用DINA模型計算P(xij=1|νij=ν,αi)，分別提出了多策略DINA（multiple-strategy DINA,MS-DINA）和混合DINA模型(mixture DINA model，Mix-DINA)。不同之處在于，前者假設不同策略的失誤和猜測參數相同，后者則假設它們隨解題策略的不同而異。另外，P(νij=ν|αi)可以通過被試總體的表現確定解題策略的分布[22-23]，也可以結合被試掌握了哪些解題策略所運用的屬性來判斷被試的解題策略[21]。除DINA模型外，其它CDM也可用于計算P(xij=1|νij=ν,αi)，例如，運用R-RUM的多策略R-RUM模型[23]。

2.多級評分項目多策略診斷樹模型

Ma[17]結合多策略模型和多級評分項目有序獨立多步驟思想，提出兩位數計分方案的診斷樹模型(diagnostic tree model,DTM)。圖1為兩種解題策略滿分為3的項目的診斷樹結構示例圖。

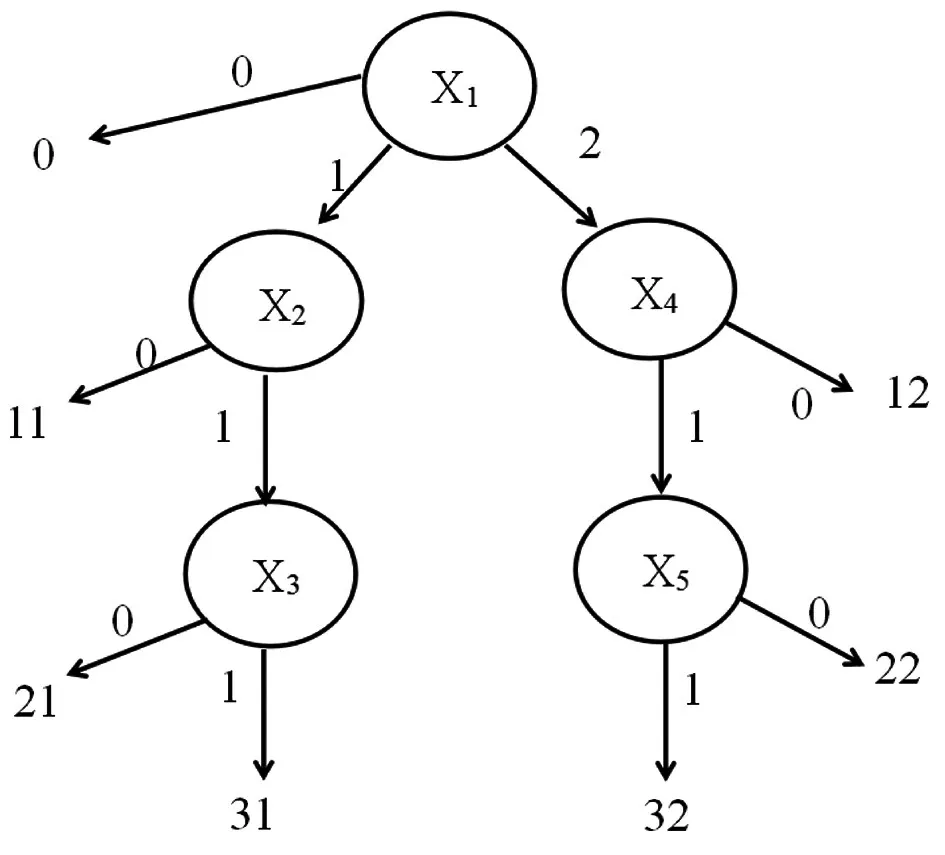
圖1診斷樹結構示例圖

診斷樹由根節點、中間節點、葉節點和路徑分支組成。其中，x1為根節點，代表作答起點，包含所有作答策略分支。每一策略可形成多條路徑。每條路徑包含中間節點（如x2,x3;x4,x5）和由兩位數構成的葉節點。其中，葉節點的個位是解題策略碼，十位是觀察得分碼。

于是，項目j得t分可能用了不同策略，同時又需要依次完成對應路徑上的所有解題步驟。令Iνjnl表示項目j在分支v的節點n上得l分的指示函數，于是DTM表示為：

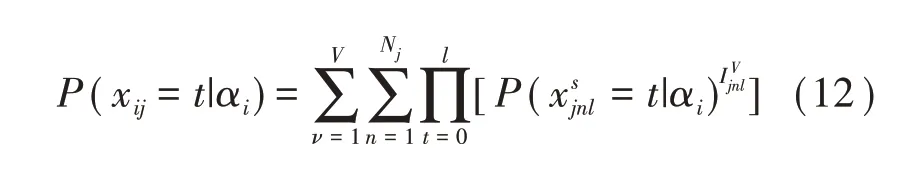
總體上講，DTM是更一般的CDM，單策略二級和多級評分模型都是其特殊形式。由于Ma（2018）應用NRDM計算故單策略多級評分項目DTM等價于NRDM。顯然，DTM中可應用其它CDM進行計算。除多解題策略外，認知診斷分析還常將屬性分為多級掌握水平。特別是當認知屬性粒度較大、包含內容較多時，二級掌握水平過于粗糙。因此，探索屬性多級CDM也具有重要意義。

（二）屬性多級CDM

屬性多級情況下，q向量和α的元素都取值為多個水平。于是，最直接的方法是首先將多級向量q和α合理轉化為二級向量q'和α'。事實上，只要qjk≥1就 有q'

jk=1。同時，只有當αik≥qjk時，才有代入G-DINA、DINA和RRUM模型就能得到屬性多級CDM，分別記為PG-DINA、PA-DINA和PA-RRUM模型[24-25]。詹沛達，邊玉芳和王立君還對PG-DINA、PA-DINA和PA-RRUM進行重參化改寫，得到更簡單更易于理解的等價模型[26]。CDM不僅從單測驗情境向復雜測驗條件發展，還結合IRT與結構方程模型思想，從低階離散知識狀態模型發展到連續潛特質與離散知識結構結合的高階模型。

五、高階認知診斷模型

de la Torre和Douglas[27]首次根據兩參數logistic模型建構了高階潛在特質與知識狀態的關系，即：

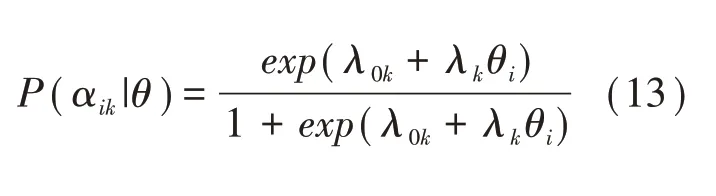
高階DINA（high order-DINA,HO-DINA）模型通過路徑難度λ0k和區分度λk建立了高階潛在特質θ與屬性αik的關系，可用于模擬研究和實證數據分析。特別地，HO-DINA中θ指各個屬性共同相關的那部分潛在特質，與IRT中的θ意義不同，但二者通常存在中高等相關。HO-DINA模型對于推測被試離散的α和θ開拓了新的視角和方法，具有重要應用價值。例如，趙頂位和戴海琦運用HO-DINA模型對4～8年級學生幾何類比推理中所涉及的七個認知屬性進行診斷評估[28]；涂冬波，蔡艷和戴海琦研究了HO-DINA模型下計算機化自適應測驗的選題策略[29]。

HO-DINA模型可以從高階和低階模型兩個方面進行擴展。例如，涂冬波等，易芹，田偉，楊濤，辛濤和劉彥樓分別用P-DINA和G-DINA計算HO-DINA中低階的DINA模型得到了多級評分HO-DINA模型和高階G-DINA模型[29-30]。又如，王丹[31]將HO-DINA中高階的單維IRT模型推廣到多維IRT模型，提出了多維HO-DINA模型，并將其應用于分析幾何類比推理測驗。結果發現，多維HO-DINA與HO-DINA的結果一致，且多維HO-DINA的應用范圍更廣。特別地，HO-DINA是HO-GDINA、HO-PDINA和MHO-DINA的特殊形式。高階模型以CDM為低階模型，以IRT模型為橋梁，連接了潛在特質與知識狀態，符合實際情況，可視作更具一般化的CDM。

六、總結與展望

CDM是認知診斷理論研究的核心，朝著多角度向縱深方向交錯發展。G-DINA模型作為二級評分項目的基礎模型，是多種常用CDM的一般形式。于是，圍繞G-DINA模型容易建構以多級評分、復雜測驗條件和高階三條主要發展分支的診斷模型樹狀圖（圖2）。從圖2可知，在各個分支上幾乎都有常用CDM的擴展模型。其中，DINA模型作為最簡單的約束化G-DINA模型，是擴展得最全面的基礎模型之一。以G-DINA模型為核心的樹狀脈絡圖涵蓋了多類重要的參數化認知診斷模型，對于厘清模型發展方向具有重要意義。總結CDM的發展不難發現以下問題還值得關注和深入研究。

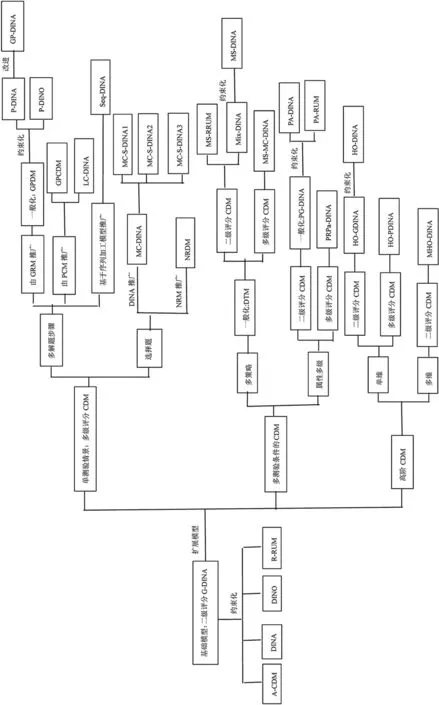
圖2

首先，模型發展不均衡。限于篇幅，本文僅概述了幾類依據項目特征發展的模型。不難發現，多級評分項目CDM是主體，多策略、屬性多級和高階模型的研究有待完善并進行比較。雖然CDM還朝著復雜測驗條件發展，例如多級評分多策略模型、多級評分高階模型、多級評分屬性多級模型[32]、多策略多選題模型（MS-MC-DINA）[33]、多階認知診斷模型[34]，但是相關研究顯然不夠。此外，除項目特征外，研究者還將某些被試變量，如反應時間、判定正確答案為正確的程度或者認可某一說法的程度等，視為因變量，建立了連續DINA模型和連續G-DINA模型[35]。因此，基于被試特征的診斷模型也具有重要研究意義。

其次，CDM的一般化發展趨勢明顯。G-DINA、GPDM、Seq-GDINA、DTM和HO-DINA都可視作特定測驗條件下的一般化CDM。例如，過程函數是Seq-GDINA的核心，除G-DINA外，可用任何CDM來計算過程函數，甚至每個得分類別都可運用不同的CDM，從而Seq-GDINA具有一般模型框架。于是，未來研究既可以比較特定條件下約束化CDM的表現，還可以探索一般化模型之間的關系、結合多測驗條件發展一般化綜合模型。

再次，一般化CDM的參數估計、模型擬合方法可以在一定程度上統一CDM的參數估計與模型擬合算法。目前，無論是相同模型不同估計方法間的比較，還是相同方法不同模型的對比研究都甚少。于是，研究和比較一般模型的參數估計和模型擬合方法具有重要意義。

最后，當前研究集中于CDM的理論開發與模擬，實證研究以語言測試、數學測試、學科素養測試居多。未來研究還應加強CDM在心理、教育甚至社會測量和計算機自適應測驗等領域的實踐應用。