基于最小二乘法的電容式電池均衡系統研究*

管 宇 ， 李 乾 ， 陳文興

（柳州工學院汽車工程學院，廣西 柳州 545616）

0 引言

溫室效應、能源緊缺等一系列問題威脅著傳統汽車產業的可持續發展，新能源汽車是解決這些問題的重要手段。電池汽車作為新能源汽車的典型代表，采用動力電池作為整車動力來源，是整車的核心[1]。電動汽車的安全性、動力性取決于動力電池的性能，而鋰離子電池具有輸出功率大、不存在記憶效應、重量輕等優點，廣泛應用于目前的電動汽車中[2]。但鋰離子電池在制造過程中還存在著一些尚未解決的問題，其中電池的不一致性問題對整車的續航里程、安全性能等指標影響最大，在電池組長期使用過程中，其不一致性會逐漸惡化，電池的容量、電壓等參數會變得愈加不理想，并且這種現象是不可逆的。因此，對電池進行均衡管理是必要的，而電容式主動均衡由于能量利用率高、均衡速度快，已成為國內外電動汽車均衡技術的研究熱點。

1 均衡系統電路結構與工作過程

1.1 均衡電路結構

均衡方案主要分為主動均衡與被動均衡兩類。被動均衡指將單體電池中的能量轉化為熱能消耗掉；主動均衡指通過能量轉移載體進行能量的轉移，根據能量轉移的中間載體不同，主動均衡主要分為電容式、電感式、變換器式三類[3]。以電容式均衡系統為例進行研究，設計出以電容為中間儲能單元的電路模型。該電路模型以兩個單體電池B1、B2構成一個模塊，MOSFET晶體管M1、M2、M3、M4是均衡控制元件，通過MOSFET管控制相鄰兩個單體電池之間的能量均衡。

1.2 能量均衡工作過程

電容“充電”過程：電壓傳感器實時檢測單體電池B1、B2的電壓U1、U2，并將電壓信號傳至均衡控制中心，控制中心根據此信號判斷是否開啟或斷開均衡電路。假設B1的內阻R1大于B2的內阻R2，則B1的電壓率先達到極限值，若U1、U2的差值達到均衡開啟的閾值，則晶體管的M1、M3的柵極G收到觸發信號后導通，此時電池B1、電容C1、晶體管M1、M3構成回路，電容C1將電池B1的電能轉換為電場能儲存起來，充電過程結束后M1、M3截止，電容C1的充電過程完成。如圖1所示。

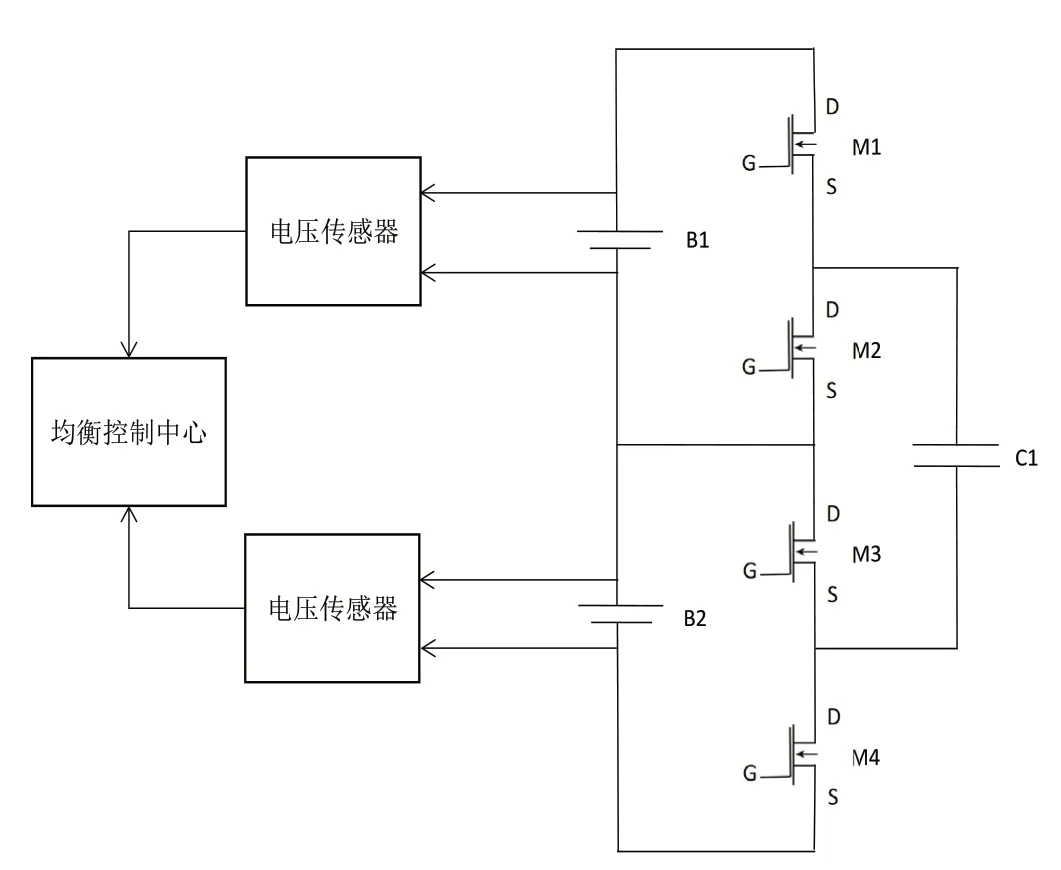
圖1 電容式均衡電路模型

電容“放電”過程：若U1、U2的差值達到均衡開啟的閾值，均衡電路開啟，能量轉移原理與電容“充電”過程相同，即M2、M4導通，電池B2、電容C1、晶體管M2、M4構成回路，此時儲存在電容中的電場能轉換為電能對B2進行充電，充電完成后，M2、M4截止。完成這個過程后，實現電池B1和B2之間的能量傳遞。

2 均衡系統能量轉移數學模型分析

2.1 高能量單體電池給中間儲能載體轉移能量

選擇以電容作為能量轉移的中間載體，均衡過程分為電容充電、放電兩個過程。

設U1表示電池單元B1的初始端電壓，uC1表示電容C1的端電壓，R1為電路模型總內阻，根據KVL，充電到t時刻電壓平衡方程為：

高能量單體電池給電容轉移能量過程的微分方程為：

2.2 中間儲載單元給低能量單體電池轉移能量

在電容放電過程，電容C1向單體電池B2充電。設U2表示電池單元B2的初始端電壓，R2表示電路模型的總內阻，uC1表示電容C1的端電壓，根據KVL，充電到t時刻的回路電壓平衡方程為：

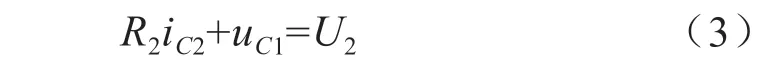
電容給低能量單體電池轉移能量過程的微分方程為：

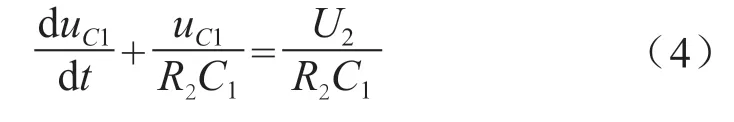
2.3 均衡系統傳遞函數

設式（2）中uC1、U1對應的象函數分別為C(s)、F(s)，微分算子用復變量s表示，在零初始條件下對式（2）進行拉普拉斯變換得到電容C1在充電過程的傳遞函數為：

設式（4）中uC1、U2對應的象函數分別為C(s)、F(s)，微分算子用復變量s表示，在零初始條件下對式（4）進行拉普拉斯變換得到電容C1在放電過程的傳遞函數為：

3 系統時域分析

通過對系統進行時域分析，可根據系統輸出量直觀、準確地分析系統的暫態和穩態性能[4]。

3.1 一階系統時域分析

一階系統傳遞函數的標準形式為：

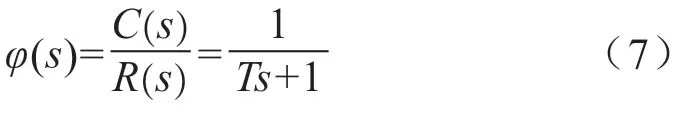
式中，T為時間常數，當系統輸入信號為單位階躍信號，即r(t)=1(t)，并進行拉普拉斯逆變換，得一階系統的單位階躍響應為：

時間常數T越小，系統階躍響應越快[5]。因此，取時間常數T=1對均衡系統進行時域分析。

3.2 均衡系統時域分析

為提高均衡系統輸入信號的可靠性，以相鄰兩電池電壓差作為均衡目標，使用最小二乘法對均衡系統進行時域擬配，求取系統階躍響應曲線，研究系統輸出量隨時間的變化關系[6]。

3.2.1 電容充電過程的時域分析

由式（5）可知，電容在充電過程系統的傳遞函數為：

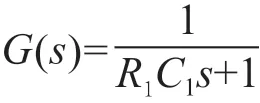
在仿真軟件系統中，使用tf函數搭建均衡系統并繪制單位階躍響應曲線。使用仿真軟件系統提供的交互工具數據游標獲取系統性能指標。在暫態過程，描述控制系統時域響應的性能指標通常有最大超調量、峰值時間、上升時間[7]。最大超調量指系統輸出超過輸入終值的最大偏移量，上升時間指系統響應從終值的0.1至0.9需要的時間[8]。從單位階躍響應圖中可知，系統的最大超調量為0，上升時間為2.1 s，峰值時間為7.64 s。在穩態過程，穩態誤差的終值為0。

采用最小二乘法獲取均衡系統輸入信號。使用c2d函數對均衡系統傳遞函數進行離散化，得到系統離散模型。當系統傳遞函數最高只有一階信號時，通常選擇單位斜坡函數作為系統輸入信號，根據輸入輸出數據構建系數矩陣，根據最小二乘法原理對系數矩陣進行辨識，得出系統輸入的擬合值，將其代入離散系統，并使用d2c函數將辨識后的離散系統轉化為傳遞函數為：

作最小二乘法辨識后系統的單位階躍響應圖可知，經最小二乘法辨識后的系統的最大超調量為0，上升時間為2.1 s，峰值時間為6.87 s。穩態誤差的終值為0。有效提高了均衡系統輸入信號的可靠性，縮短了均衡時間，降低了不一致性問題帶來的影響，具有更好的均衡效果。

3.2.2 電容放電過程的時域分析

由式（6）可知，電容在放電過程系統的傳遞函數為：

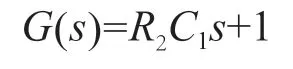
在仿真軟件系統中，使用tf函數搭建均衡系統并繪制單位階躍響應曲線。從單位階躍響應曲線可知，系統的最大超調量為0，系統響應從終值的0.1至0.9需要的時間約為2.1 s，峰值時間為6.34 s。

采用最小二乘法獲取均衡系統輸入信號。使用c2d函數對均衡系統進行離散化。選擇斜坡函數作為系統輸入信號。根據系統輸入輸出數據構建系數矩陣，并根據最小二乘法原理對系數矩陣進行辨識，得出系統輸入的擬合值，將其代入離散系統，并使用d2c函數將離散系統轉化為傳遞函數為：

作最小二乘法辨識后系統單位階躍響應曲線可知，經最小二乘法辨識后的系統的最大超調量為0，系統響應從終值的0.1至0.9需要的時間約為2.1 s，峰值時間為5.86 s。與算法辨識前的系統相比，提高了系統輸入信號的可靠性和均衡時間，有效降低了電池組中各單體電池存在的不一致性問題，提高了電池組整體性能，延長了電池組使用壽命，符合最小二乘法的實際辨識效果。

4 設計

4.1 均衡系統模型搭建

課題組采用仿真軟件系統根據設計的電路結構搭建均衡系統模型并進行仿真驗證，均衡系統模型由系統啟停控制模塊、控制模塊、電池組模塊、均衡電路模塊四部分組成。

4.2 均衡系統仿真分析

系統仿真模型搭建完成后，進行仿真參數的設置及仿真結果的運行、分析。通過Powergui模塊，可以對系統進行定步長離散系統仿真[9]。根據系統性質將仿真類型選擇為Discrete（離散型），仿真算法選擇ode45算法[10]，其余參數保持系統默認值。

單擊模型窗口中的“RUN”選項，系統開始仿真。仿真結束后，通過示波器模塊觀察系統仿真結果。通過仿真結果可知，電池組B1、B2電壓值逐漸趨于一致，實現電池組間能量轉移。

5 小結

綜上所述，鋰離子電池作為車用電池時常將多個單體電池串聯或并聯成電池組使用，由于其生產制造和使用中的差異，在經過多次充放電后，電池組內各個單體電池的容量、功率、壽命等參數會發生變化，出現不一致性問題。該現象對動力電池的安全性能、續航里程、使用壽命都會產生嚴重影響，并且是不可逆的。針對電池組不一致性問題，對電池均衡技術展開研究，使用最小二乘法對電路模型的數學模型進行參數辨識，提高均衡系統輸入信號可靠性，并在仿真軟件系統中設計出一套均衡系統仿真模型，通過均衡系統降低電池在生產和使用過程中產生的不一致性問題帶來的影響，從而提高動力電池組的使用容量與壽命。