有限長序列循環卷積的求解
任蕾
(上海海事大學信息工程學院,上海 201306)
1 引言
線性卷積和循環卷積是信號處理類課程教學的重要知識點。二者的定義、常用性質、計算方法和異同點也是教學的難點之一。離散線性時不變系統的零狀態響應可通過激勵序列與系統的單位脈沖響應卷積求得。
陳輝金在文獻1中提出了圓周卷積的豎式求解方法,該方法的本質是在線性卷積的對位相乘法基礎上拓展而來的,利用了圓周卷積是線性卷積的周期延拓這一結論,該方法簡單易學,便于學生理解圓周卷積的本質[1]。文獻2 在分析循環卷積與線性卷積關系的基礎上提出了一種基于序號和匹配的簡單循環卷積求解方法[2],該方法與文獻1的方法本質是一致的,充分利用了參與卷積的序列之間的關系。文獻3 則從線性卷積和循環卷積的基本概念入手,探討了其運算規則和等價條件,并提出了一種利用線性卷積快速計算循環卷積的方法[3]。此外,與科研相結合的循環卷積的教學探討也有相關報道。戚晨皓等結合通信中的正交頻分復用技術,介紹了循環卷積的應用[4]。文獻5 結合水聲通信領域的應用,介紹了基于線性卷積的循環卷積計算方法及其在該領域的應用[5]。
目前常用的循環卷積計算方法主要包括定義法、圖解法、列表法、對位相乘法、變換域方法、矩陣矢量相乘法、Matlab 求解等。特別的有限長序列的卷積是實際數字系統中常見的運算,其卷積結果仍是有限長序列。本文首先介紹線性卷積和循環卷積的基本定義,進而針對有限長序列的循環卷積的計算進行方法總結和梳理,并結合實際例子說明各類方法的應用過程。
2 線性卷積與循環卷積
2.1 有限長序列的線性卷積與循環卷積
有限長序列x1(n)(0≤n≤N1-1) 和x2(n)(0≤n≤N2-1)的線性卷積[6]yl(n)為:
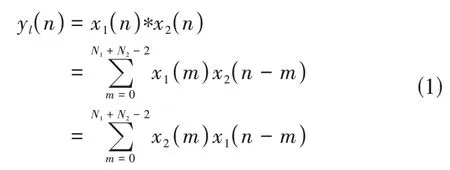
即兩個有限長序列的線性卷積,其序列長度不會超過N1+N2-1。
上述兩有限長序列的L點循環卷積[6]yc(n)定義為:
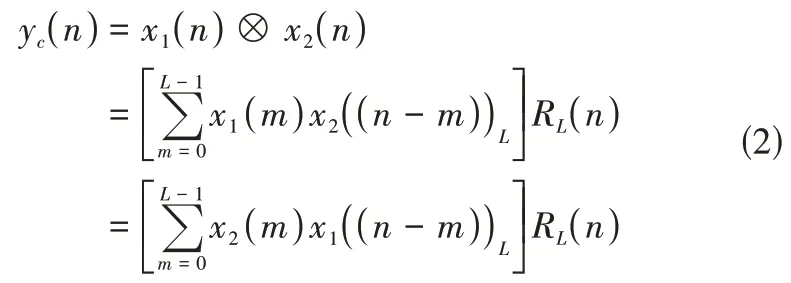
則兩有限長序列的循環卷積與線性卷積的關系[6]為:
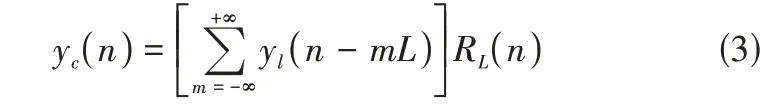
即循環卷積是線性卷積以L為周期進行延拓后構成序列的主值序列。當滿足L≥N1+N2-1時,循環卷積和線性卷積一致,否則,部分時刻的卷積和序列會混疊。
2.2 循環卷積各類計算方法總結及對比
考慮到循環卷積與線性卷積的聯系,有限長序列的循環卷積可借鑒線性卷積的方法實現,包括定義法、圖解法、對位相乘法、矩陣矢量相乘法、變換域方法和利用Matlab的求解方法等。表1 總結了目前有限長序列循環卷積的主要求解方法[1-3,6],并對其進行簡要介紹。

表1 有限長序列循環卷積求解方法總結表
上述方法中基于定義式的計算方法直接從定義出發,是最基本的一類方法,過程較為煩瑣。對位相乘法、豎式計算法、序號和匹配法以及圖解法等這類方法均是基于循環卷積的基本定義,對參與卷積的序列進行適當的排序、移位、相乘和疊加來進行的,其本質是一致的,只是在序列的排列和計算順序上有所區別。其中,基于線性卷積和循環卷積關系的對位相乘法最直觀簡便,可以直接從線性卷積的結果進行適當的循環移位及疊加后得到循環卷積結果。
矩陣與矢量相乘法,其關鍵是構建循環卷積矩陣[6],由式(2)定義循環卷積矩陣:
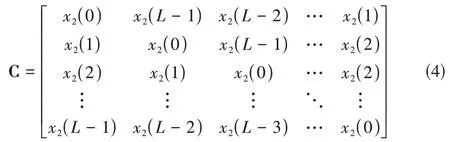
則循環卷積得到的序列yc(n)可由矩陣C與x1(n)構成的列矢量相乘求得:

同理,由交換律,也可由序列x1(n) 構造相應的循環卷積矩陣來實現計算。
變換域方法,則首先計算補零后的x1(n)和x2(n)的L點DFT,分別為X1(k)和X2(k),其結果逐點相乘并進行逆變換求解循環卷積序列,該方法可借助快速傅里葉變換實現。
最后,應用Matlab 軟件也是求解循環卷積的常用方法,根據是否直接調用內部函數可以細分為直接調用方法、矩陣矢量相乘法、變換域實現方法等。Matlab 中的循環卷積內部函數為:cconv(a,b,n),其中a和b是參與循環卷積運算的序列矢量,n是循環卷積的點數。其他兩類情況則需要編寫相關的程序實現,詳見文獻6的相關章節[6]。
3 有限長序列的循環卷積求解舉例
本節給出典型例題,并詳細介紹幾類循環卷積的求解方法。
例題1:已知序列x1(n)=和x2(n)=,計算4點循環卷積y(n)=x1(n)?x2(n)。
解:由于文獻1-3涉及的方法有類似之處,僅給出文獻1的方法以及其他部分方法的求解過程。
1)定義法
4點循環卷積的每一點由下式給出:

2)對位相乘法
這里的對位相乘法是在有限長序列的對位相乘法基礎上增加了序列的周期化得到的,即文獻1 中所述的豎式計算法,本題的演示過程如圖1所示。首先將兩序列右側對齊,第二個序列的每個序列值逐個與第一個序列相乘、移位并求和得到線性卷積的結果,進而根據題意求4 點的循環卷積,則需要將線性卷積結果以4 為周期進行周期化,疊加后的序列選取其0~3時間區間內的結果就是循環卷積結果。從下列過程也可以看出,該方法直觀、簡便,同時清晰地顯示出線性卷積和循環卷積的關系。
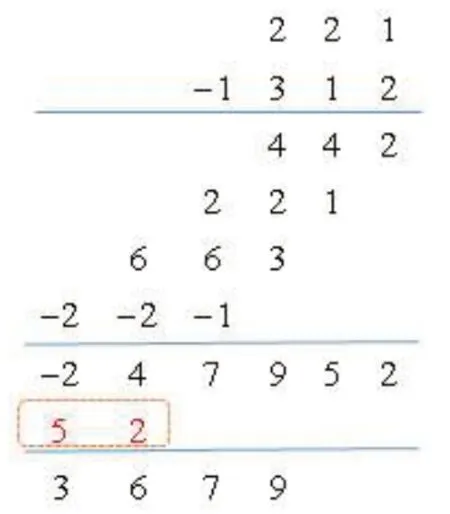
圖1 例題1的對位相乘法計算過程
3)矩陣矢量相乘法
矩陣與矢量相乘的方法核心問題是構造循環卷積矩陣,由式(4)可得本題中的循環卷積矩陣為:
4)變換域方法
變換域方法求解循環卷積時,首先需要求解兩序列的4點DFT,分別為:
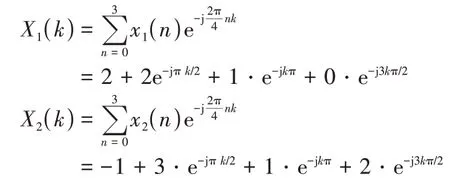
將k=0,1,2,3代入,可得:
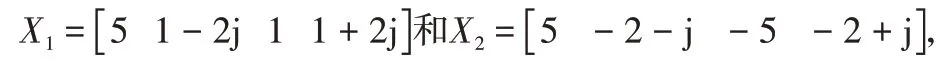
對上述序列進行逐點相乘有:
Y(k)=,因此對其進行逆變換得序列:
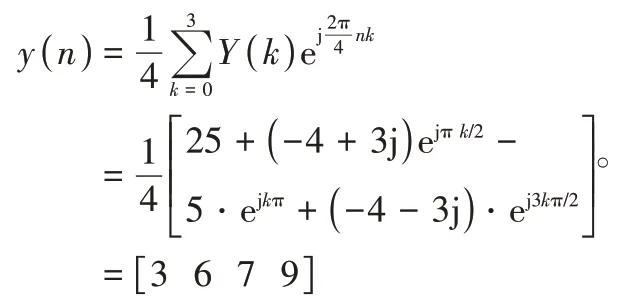
5)Matlab求解方法
Matlab 中的循環卷積的計算函數為cconv(a,b,n),設置輸入參數可以直接求解,本例中兩序列、線性卷積和循環卷積的波形如圖2所示。
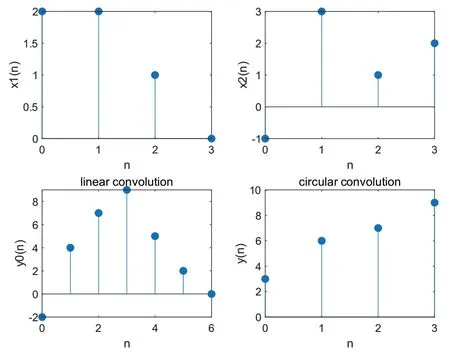
圖2 循環卷積的Matlab求解波形圖
其次,該例題也可通過變換域方法實現,即分別計算兩序列的DFT,在變換域中頻譜相乘,再進行逆變換,兩信號及循環卷積的序列時域和幅度譜如圖3所示。
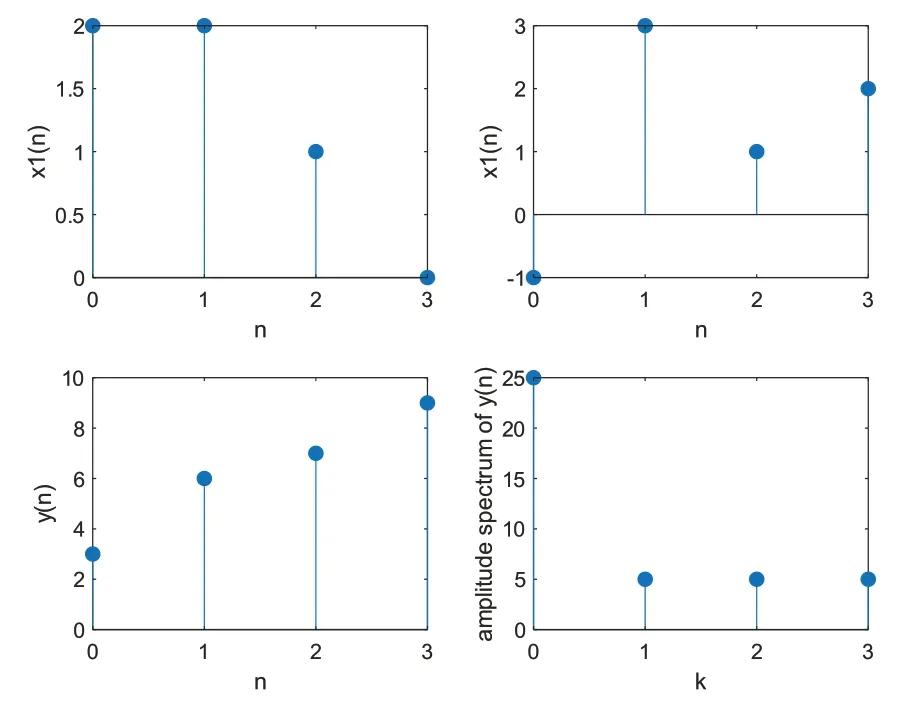
圖3 利用DFT求解循環卷積的波形圖
再次,在Matlab中也可利用矩陣矢量相乘的方法實現循環卷積的求解,可利用toeplitz函數構造循環卷積矩陣實現。循環卷積實現的程序如下[6]:

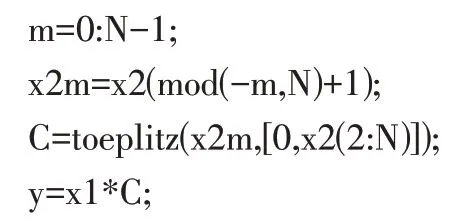
輸入已知序列后,應用上述程序也可得到同樣的卷積結果。
例題 2:已知序列x1(n)=和x2(n)=,計算8點循環卷積y(n)=x1(n)?x2(n)。
解:由于本例中的序列x1(n)和x2(n)的線性卷積序列長度不超過8,因此本例中的循環卷積和線性卷積的結果一致,可借鑒線性卷積的各類方法來求解。
1)列表法
由于列表法是線性卷積的常用方法[6],按照翻轉、移位、相乘、疊加的步驟進行卷積運算,下面給出列表法的計算過程:
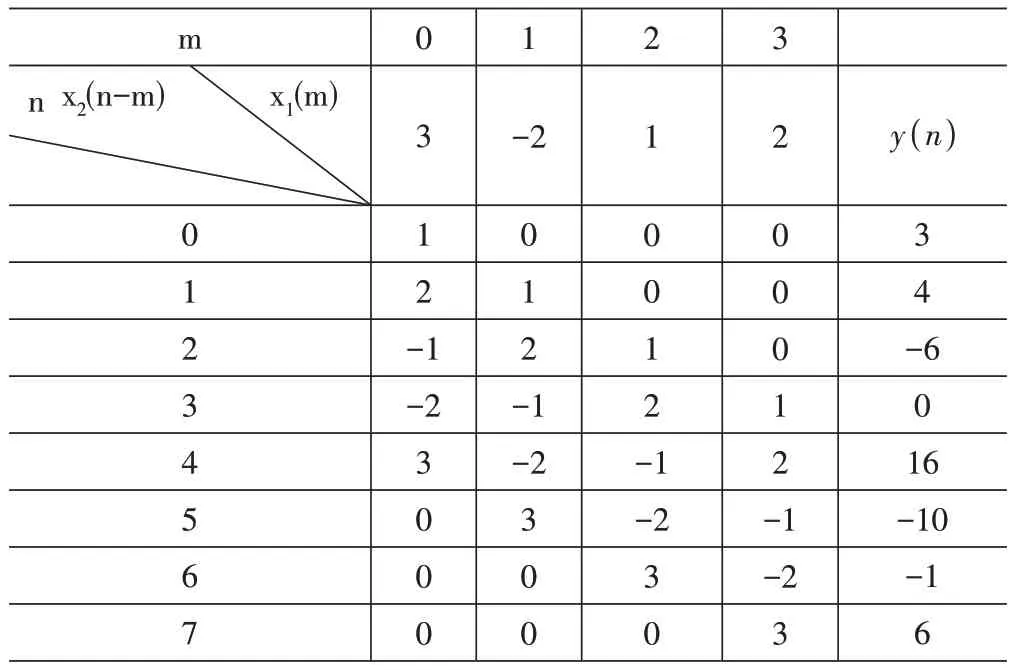
表2 例題2的列表法求解
2)對位相乘法
將兩序列右邊對齊,依次相乘、移位、疊加,此例題中線性卷積和循環卷積的結果一致。

圖4 例題2的對位相乘法計算過程
3)Matlab求解方法
由于本題的特殊性,除直接調用conv(a,b,n)函數實現該例題的卷積運算外,也可通過變換域方法實現,其程序如下所示:

輸入序列x1(n)和x2(n)后,應用上述程序可得:y(n)=。該題目中各序列的波形如圖5所示:
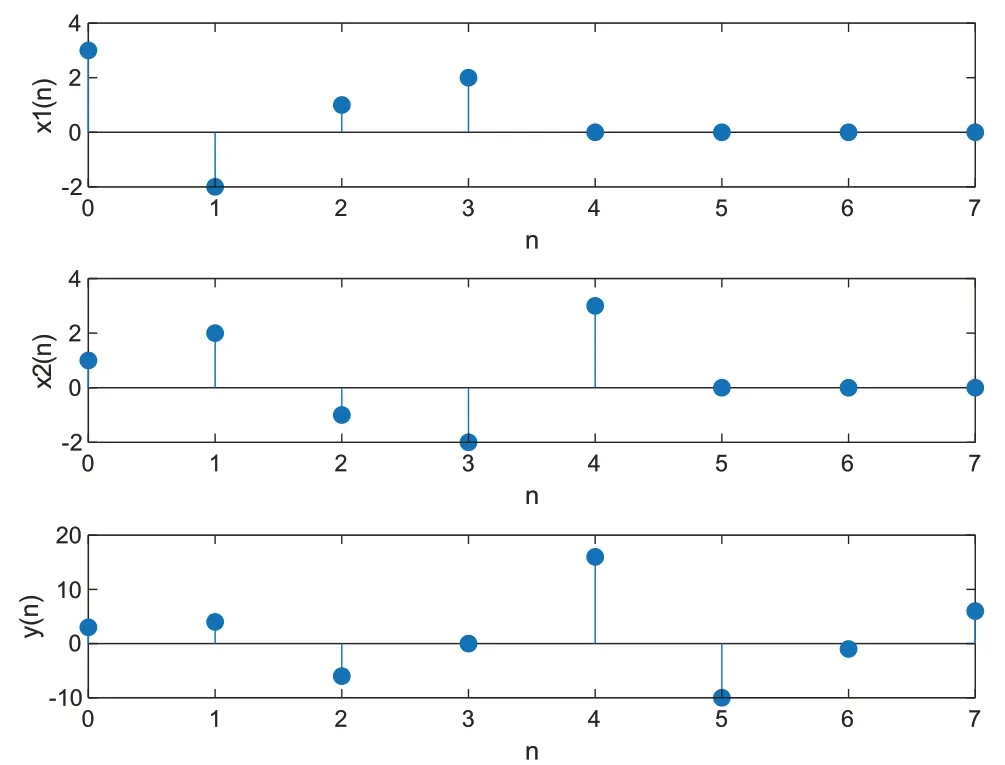
圖5 例題2中序列和卷積結果的波形圖
上述例題的求解過程再次驗證了線性卷積和循環卷積的關系,以及此類運算的本質。對應不同的求解思路,在Matlab中也有相應的實現方法,即可直接調用內部函數,也可通過變換域方法、矩陣矢量相乘的方法來求解。若循環卷積的點數大于等于線性卷積的長度時,則可應用線性卷積的方法直接計算獲得。
4 結束語
循環卷積是數字信號處理課程中的重要知識點,也是本課程學習的難點之一,循環卷積與線性卷積有密切聯系,當循環卷積的點數大于等于線性卷積長度時,二者結果一致,否則會發生混疊,因此利用循環卷積求解線性卷積時,需注意點數的選擇。利用循環卷積的定義及其與線性卷積的關系,本文梳理并總結了已有的有限長序列循環卷積的各類求解方法,并給出了相關例題,以幫助學生掌握并理解循環卷積的基本特點和求解思路。涉及到的方法也是信號處理課程中各類信號和系統分析的常用思路,包括時域和變換域等,此類方法總結也有利于學生融會貫通,從整體上更好地掌握所學知識。

