魯南地區黏性土的鄧肯張模型參數試驗分析
謝 營
(山東省水利勘測設計院有限公司,山東 濟南 250014)
本項目所選用土料取自臨沂地區,項目所在地分布地層主要為元古代晉寧期、中生代燕山晚期、元古代膠南期侵入巖體,巖性為二長花崗巖、石英閃長巖;白堊系青山群八畝地組安山質凝灰巖、白堊系大盛群沉積巖,巖性為泥質砂巖、砂巖;第四系松散堆積層,巖性主要為壤土、黏土、礫質粗砂及含砂壤土。選用項目所在地的黏土和壤土作為試驗土樣。
1 試驗準備過程
1.1 物理指標
項目采用擾動土樣,取土深度為1.0~1.5 m。根據顆粒分析試驗結果,所取土樣定名為黏土和壤土。土樣物理指標見表1。
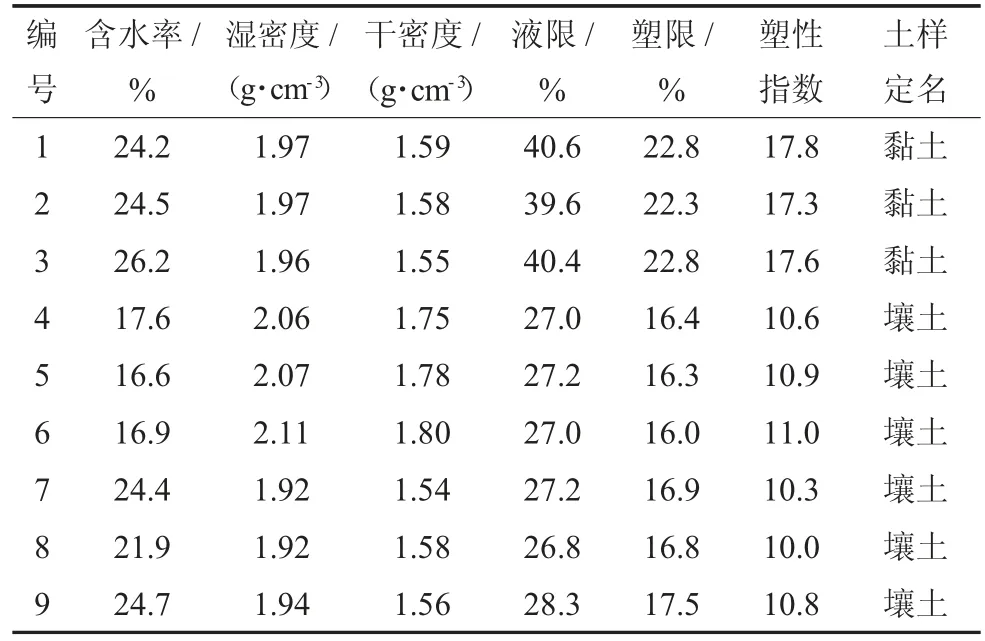
表1 土樣物理指標
1.2 擊實試驗
對所選取土樣進行風干、碾碎、過篩,篩的孔徑符合《土工試驗方法標準》(GB/T50123-2019)要求。測定風干含水率,按照要求加水并置于密封塑料袋中24 h,使含水率均勻。采用輕型擊實試驗,擊錘的質量為2.5 kg,擊實筒容積為947.4 cm3。分5層填筑擊實,擊實試驗計算結果見表2。
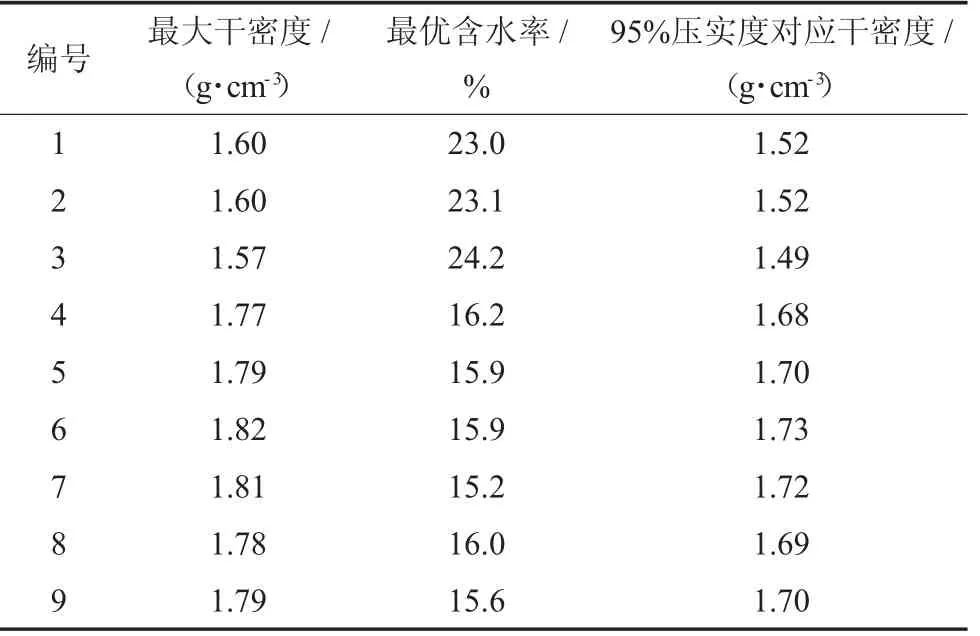
表2 擊實試驗結果
根據擊實試驗結果,采用壓實度0.95,計算對應的土樣重量和含水率,配制相應土樣,按照規范要求制備成三軸試驗所需尺寸進行試驗。
2 鄧肯張模型參數的推導
康納根據大量的三軸試驗的σ-ε關系曲線,提出可以用雙曲線擬合出常規土的三軸試驗應力應變曲線:
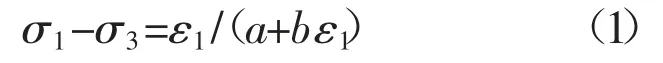
式中:a、b均為試驗參數,鄧肯等人根據這一雙曲線關系提出了到目前為止被廣泛應用的增量彈性模型,即鄧肯張模型,其中包括8個參數。
將公式(1)中ε1/(σ1-σ3)和ε1的關系近似成線性關系,其中a為截距,b為斜率,由此可以得到切線模量,見公式(2):

在試驗的起始點,ε1=0,Et=Ei,則a為起始變形模量Ei的倒數,即a=1/Ei,假設ε1趨向于正無窮,可以得到

由公式(3)可知,b為雙曲線的漸近線的極限偏差應力的倒數。
為了進一步推導模量參數,此處引入破壞比的概念,破壞比Rf:
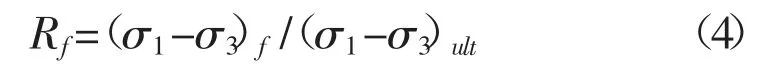
在實際試驗中,往往根據設定的應變值來確定土的強度(σ1-σ3)f,本試驗中設定應變為20%來確定土的強度。將公式(3)(4)均帶入公式(2)即可得到切線變形模量的推導公式:
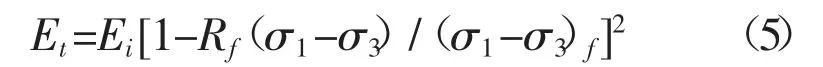
根據摩爾庫倫定律
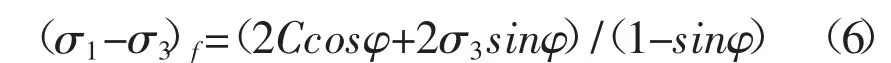
將公式(6)代入公式(5)可以最終得到公式
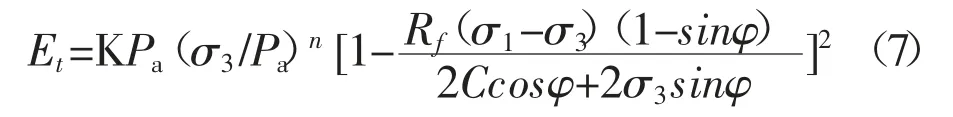
式中:n、K為試驗常數,Pa為大氣壓。由切線變形模量公式可以得到模型的5個參數K、n、φ、c、Rf。
鄧肯等人又假設軸向應變和側向應變之間也存在雙曲線關系,經過一系列演算,得到泊松比的公式:
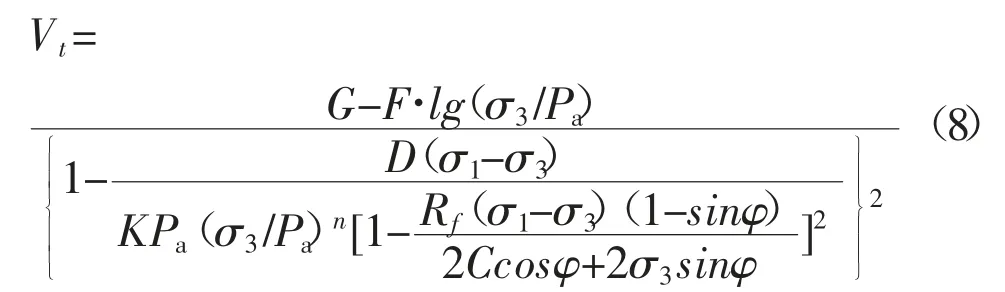
公式中引入了G、F、D3個參數,加上前面的5個參數K、n、φ、c、Rf,即為常說的8大參數。
3 三軸試驗
根據《土工試驗方法標準》(GB/T50123-2019)要求,試驗采用應變控制式全自動三軸儀采集數據,試樣尺寸為39.1 mm×8 mm,施加圍壓σ3分別為100 kPa、200 kPa、300 kPa。采用固結排水剪切,剪切速率設定為0.012%/min,剪停應變設置為20%。由三軸試驗結果進行數據分析,得到各土樣的鄧肯張模型參數見表1:
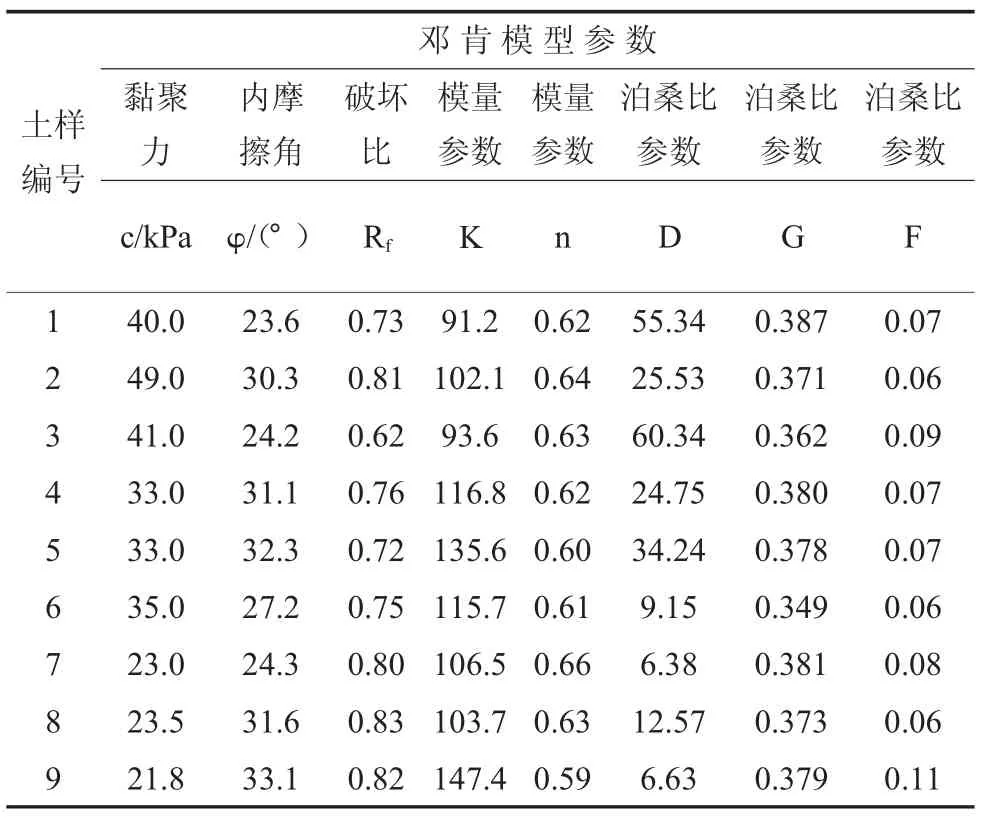
表1 土樣鄧肯張模型參數結果
由表1可知,黏土的c值高于壤土,φ值低于壤土;兩種土破壞比Rf的取值均在0.62~0.85之間;黏土的K值 在91.2~102.1之間,壤土的K在103.7~147.4之間,K值與土的強度存在有一定的正比關系,強度較高的土,K值較大;兩種土的n值大多在0.59~0.66之間,n值與土的強度存在一定的反比關系,強度較高的土,n值較低。
4 結語
鄧肯張模型廣為工程界接受并大量應用,該模型所用的參數及常數并不多,物理意義明確,應用簡便,只需要常規的三軸試驗即可確定,因而得到了極大的推廣使用。但是鄧肯張模型是建立在廣義胡克定律基礎上的變模量的彈性模型,受其理論基礎的限制,本模型也有一些缺陷,部分參數的確定受主觀因素影響較大。在工程實際應用中要了解模型的特點,因土而異,正確地使用本模型取舍數據。

