小學數學教學材料設計的四重邏輯
——基于數學是一種創造性活動

■錢中華

“數學是人類的一種創造性活動，即是一種包含有猜測、錯誤和嘗試、證明與反駁、檢驗與改進的復雜過程，特別是，我們應明確肯定數學活動的易繆性與發展性質。”[1]11數學是動態的、經驗與擬經驗的，不僅包含具體的數學知識，而且蘊含先賢發現或創造數學知識，祛除遮蔽、排除悖論所經歷的艱難探索，以及把握本質屬性的歷程。

正是在這個意義上，要求學生的數學學習在簡略經歷數學知識產生、形成、發展的歷史過程中，“去理解知識最初發現時人們面臨的問題、解決問題的思路，采用的思維方式、思考過程，理解知識發現者可能有的情感，判斷評價知識的價值”[2]，掌握數學知識本質及關系結構，改善發展數學思維，形成積極情感態度。

數學教學材料是學生學習數學的對象，是由教師對教學內容精心加工、設計而成的，體現了對“學什么”“怎么學”的核心關切。聚焦數學這種創造性活動，小學數學教學材料設計需要把握教學內容的歷史邏輯、理論邏輯、價值邏輯和實踐邏輯。

一、歷史邏輯：數學知識產生、形成、發展的歷史演變

遵循歷史邏輯要求教師從數學史的視角，考察并精準把握數學知識的起源、演進、深化與推廣，設計體現數學知識產生、形成、發展歷史演變過程的教學材料。

教師深入分析數學知識產生的歷史背景，明確從何處產生、為什么會產生的必要性；把握在歷史長河中以什么為知識原型，按照自身內部邏輯，經過逐步演進發展而形成如今的數學知識；深刻理解數學的發展“不是用破壞和取消原有理論的方式進行的，而是用深化和推廣原有理論的方式，用以前的發展作準備而提出新的概括理論的方式進行的”[3]33，明確以原有數學知識為基礎的橫向深化和縱向推廣。這樣，教師以此為依據，設計出再現數學知識演進與變化的教學材料，為學生數學學習創造親歷知識生長過程和提供再發現的機會。

例如，“分物游戲”。本課是除法運算的首課，內容是離散量“平均除”。“平均除”起源于“分”，即古代人們按只數分野兔、按個數分土豆或果子等離散量物體，發現“分”的結果可能每份同樣多，也可能每份不是同樣多，怎樣才能使得每份同樣多成為當時人們思考的問題。離散量“平均除”的演進過程：早起“分”諸如野兔、土豆、果子等離散量物體→發現有多種分法→比較不同分法的結果，發現其中一種分法分得的每份數量同樣多，這種分數概括為平均分→為了快速、準確、簡潔地平均分離散量物體，發明“平均除”。離散量“平均除”橫向深化：一位數除以一位數→兩位數及以上除以一位數→除數是兩位數或以上；縱向推廣：離散量“平均除”→離散量“包含除”→連續量“平均除”→連續量“包含除”。

教學材料設計如下：

（1）把6個蘋果分給淘氣和笑笑，可以怎樣分？

（2）按照分的結果，可以分成幾類？

（3）像這樣每份都是3個蘋果就是平均分，用除法計算，介紹除號的來歷與寫法。

（4）有12根蘿卜。每只小兔分到的蘿卜一樣多，每只小兔分到多少根蘿卜？

這組材料緊扣“平均除”起源于“平均分”，以開放性問題“把6個蘋果分給淘氣和笑笑，可以怎樣分”切入，調動學生已有經驗，將6個蘋果分成“0、6”“1、5”“2、4”“3、3”四種情況。通過解決問題（2），理解以分的結果是否相等為標準，可以把四種情況分成2類，前三種結果不相等為一類，第四種結果相等為一類。自然而然地進入材料（3），引出平均分，用除法運算。問題（4）是橫向深化，進一步理解“平均除”。縱觀整個過程，教學材料設計遵循了“平均除”形成的歷史邏輯，學生數學學習經歷了“分→平均分→平均除”過程，以深刻理解平均分為基礎創造“平均除”，并銜接了后續學習的“包含除”。

二、理論邏輯：教學內容是數學理論體系不可分割的有機組成部分

扎根理論邏輯要求教師把握教學內容是數學理論體系不可分割的有機組成部分，深入分析教學內容包含的概念、命題及其之間的邏輯關系，挖掘概念、命題形成過程中蘊含的數學思想方法；設計置于數學知識本質、關系結構及其數學基本思想的教學材料。

具體而言，教師將教學內容置于數學理論體系，把握數學知識的最終表現不是各個孤立的知識點（概念、命題），分析數學知識（概念、命題）的關系結構，包括數學知識先后順序的邏輯結構以及由數學知識構成的網狀的知識結構；把握數學知識本質不是概念、命題，也不是數學符號和數學知識的多樣化表征，分析數學知識的本源意義及內在的、不變的本質屬性。分析教學內容所滲透的數學基本思想——數學抽象、邏輯推理、數學建模，把握數學思想“蘊涵在概念的形成、規律的揭示、結論的推導以及知識發展、應用過程中，是數學知識和方法在更高層次上的抽象與概括”[4]。這樣，根植教學內容的理論邏輯進行教學材料設計，不僅可以教學正確的數學，更為重要的是學生通過學習，可以理解把握數學知識本質，建立關系結構，感悟數學基本思想。

例如，“什么是面積”。在數學理論體系視域下，其邏輯結構為：前概念（生活中的物體表面大小）→面積概念→面積單位→規則封閉平面圖形的面積（物體表面積）→不規則封閉平面圖形或物體表面的面積（知識結構見圖1）。具體到本課內容其邏輯結構為：前概念（生活中的物體表面大小）→物體表面的面積→封閉平面圖形的面積→比較平面圖形面積的大小→銜接面積單位（知識結構見圖2）。面積的本源意義是“比較”，本質屬性是“度量”；可見，教材中定義“面積是物體表面或封閉平面圖形的大小”，這是外在的邏輯形式，沒有觸及面積的本源意義及本質。面積概念形成過程中蘊含了數學抽象（比較、分類、概括、數形結合、變中不變、符號化等）、數學推理（歸納、演繹、化歸、特殊與一般等）和數學建模（簡化、量化、優化）等基本思想。由此，設計出如下三組教學材料：

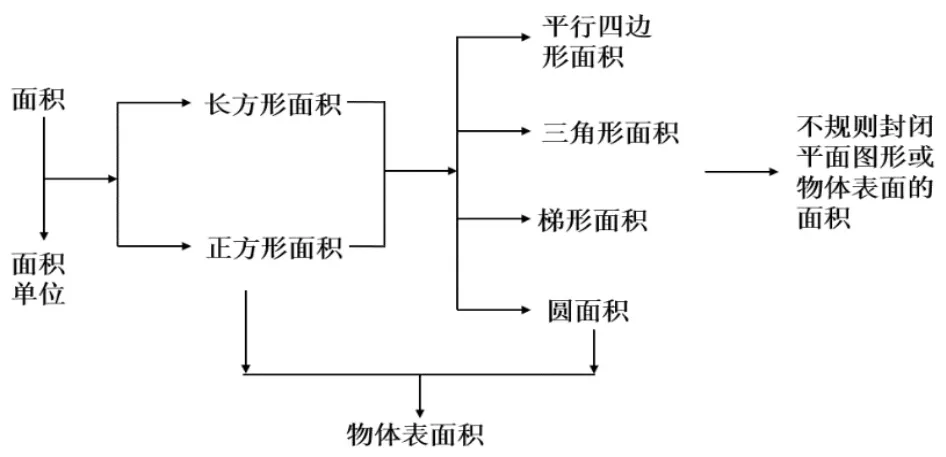
圖1 面積知識結構

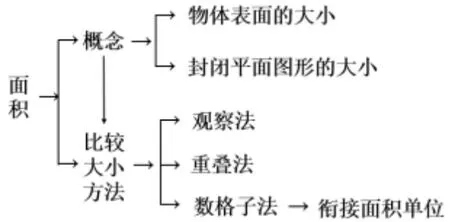
圖2 “什么是面積”知識結構

第一組問題：

（1）數學教科書封面和A4紙誰大？這個大小你們知道比的是什么？

（2）既然比的面積，那么，面積與什么相關？

（3）教科書封面和A4紙表面是規則的有面積，樹葉的表面是不規則的，有面積嗎？理由是什么？

第二組問題：

（1）物體表面有面積，平面圖形有面積嗎？

（2）下面這些平面圖形有面積嗎？為什么？

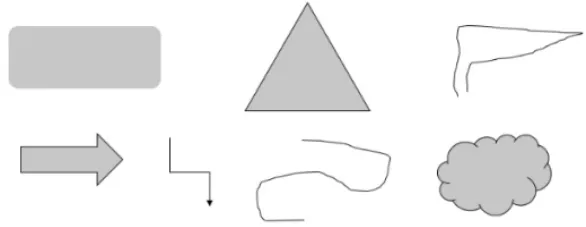
圖3

第三組問題：

（1）A和B誰的面積大？用什么方法比較的？

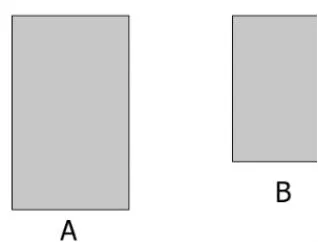
圖4

（2）C和D誰的面積小？用什么方法比較的？

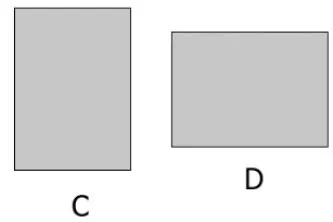
圖5

（3）E和F誰的面積大？可以怎樣比較？

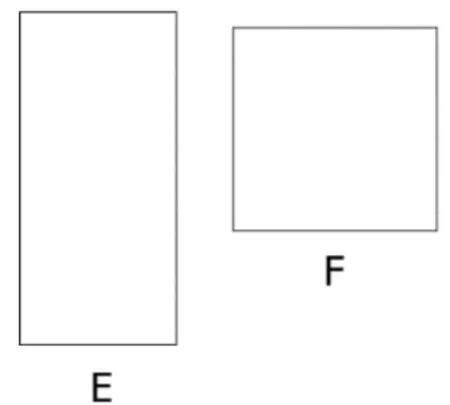
圖6

（4）用“數格子法”可以比較E、F面積的大小。其實質就是用“格子”去測量E、F，這里對“格子”有何要求？

（5）淘氣和笑笑兩家在裝修新房時，都用了70塊地磚鋪滿客廳，他們兩家客廳的面積一樣大嗎？

這三組教學材料，扎根“度量”，凸顯了“比較”的本真意涵；將面積的邏輯結構、知識結構轉化為學生學習易于接受、可以觸摸的結構化的材料，并將數學抽象、邏輯推理、數學建模蘊含其中，幫助學生深刻理解面積的本質意義，建構面積概念的邏輯結構、知識結構，領會數學基本思想，銜接面積單位學習。

三、價值邏輯：通過數學學習發展數學思維

站位價值邏輯要求教師“忠誠學科教育的本質追求，切實體現學科的教育價值取向和育人本質，完整達成學科教學目標而體現出來的高階發展性品質”[5]，把握數學教學的根本價值是培育學生的數學思維。教師深入教學內容，剖析數學思維形式方法，精準把握數學思維形式方法類別，進而進行教學材料設計。如此，學生在數學學習活動中，開啟思維操作，在探索和理解數學知識最深刻的和最完美的內涵過程中經歷數學思考，理解不同數學思維形式方法的發生機制、應用范圍及遵守的規則，改善發展數學思維，提升數學思維品質。

例如，“數對確定位置”。從數對產生的必要性、數對表示位置的唯一性、數學符號表征的簡明性三個方面展開理解數對，蘊含了分析、比較、分類、抽象、概括、判斷、推理等數學思維形式方法。基于此，教師以問題取向、過程取向、社會取向，設計出如下教學材料[6]：一是ppt展示老師讀初中時的舊照片，請同學們找出老師站在哪個位置并表示出來；二是用自己的記錄方式介紹老師，看能不能在照片中準確、快速地找到老師，如果不能該如何改進；三是老師所站位置除用數對（3,5）表示外，看還能不能用其他數對表示。

統觀教學材料，以問題開啟學生思維操作，意義建構數對。首先以開放性問題調動學生已有經驗，經歷觀察、分析、分類、判斷、概括的思維活動，從不同視角運用不同分法記錄老師所站位置，培養思維的靈活性；第二個問題引發學生思辨多種記錄方法的內在關聯并捕捉矛盾，經歷嘗試、猜想、驗證、推理、反思與評估的思維過程，理解記錄老師位置必須有確定的行數和列數，以及規定行前列后的合理性，培養思維的深刻性；第三個問題引起學生猜想、嘗試、驗證、判斷、推理、論證，理解數對表示位置的唯一性及數學符號表征的簡明性，發展洞察力、辨別力、判斷力，培養思維的批判性。整個過程不僅體現了學生數學學習運用數學思維形式方法解決問題，而且體現了在解決問題中獲得數學思維的改善發展，也培養了包括靈活性、深刻性、批判性在內的數學思維品質。

四、實踐邏輯促進經驗重組與意義建構

筑牢實踐邏輯要求教師深度分析學生已有（生活、認知）經驗，明確最近發展區，設計歷史邏輯、理論邏輯、價值邏輯融為一體的教學材料。

教師立足教學內容，從教材邏輯、自我經驗、教師團隊經驗、前測調查等路徑分析學生已經知道了什么，把握好學生已有（生活、認知）經驗與所學內容之間的距離，找準學生數學學習的生長點和著力點，重構“符合史實，而不是胡編亂造，不能有科學性錯誤；建立在學生已有的生活經驗和認知基礎之上，凸顯其必要性”[7]424-426的“現實性”與“問題性”整體融合的教學材料，驅動引領學生數學思考辨析，改造重組經驗，意義建構知識。

例如，“生活中的比”。教師設計了“①看見“比”，您想到了什么？②在日常生活中，您聽說過哪些比？③寫一個比，并舉例說明”三個問題，前測調查學生對“比”的生活、認知儲備，了解到學生：①會寫比和用除法運算求比值；②對同類量的比有所了解；③對同類量的比是比倍有所了解；④在生活中了解到比是球類比賽的比分或沙、水泥、水的配比。存在的問題：①對不同類量的比缺乏了解；②認為比就是除法運算，對比的本質缺乏了解；③不清楚比不僅可以表示兩個量的關系，也可以表示三個及以上數量的關系；④絕大部分學生不能借助生活實例解釋比的意義。在此基礎上，把握比最初是幾何中兩個同類量的度量，也就是確定一個單位標準去測量另一個同類的量，就得到一個比，兩個同類量是倍數關系；度量實際是比較。后經眾多數學家對其擴展，比從幾何領域逐步進入算術，進而進化到不同類量的比和兩個數的比，用除法運算求比值。這一演變過程表明：比產生的根本原因是比較；演進路徑是從幾何到算術，從同類量到不同類量。把握比的數學本質是兩個數量之間倍數關系的表達或度量，不是除法運算；明確內隱的數學基本思想、數學思維。

再進一步分析學生對比認識的已有（生活、認知）經驗與比的歷史演變的符合程度，設計教學材料順序；分析學生對比認識的已有（生活、認知）經驗與比概念原型之間的差異，選擇設計現實性教學材料；分析學生對比認識的已有（生活、認知）經驗與比的數學本質之間的“距離”，設計激發認知沖突的問題性教學材料；三者統整，重構出“生活中的比”的教學材料。

第一組：

（1）觀察屏幕上的圖形（圖7），你有哪些發現？這些發現可以分成幾類？有什么相同點和不同點？

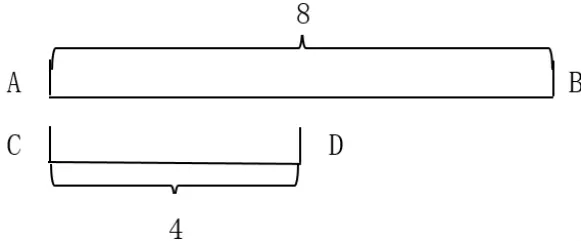
圖7

（2）AB是CD的2倍，即8是4的2倍，稱為8比4，記作8:4，8是前項，4是后項，“：”叫比號；通過8÷4得到8:4的結果是2，叫比值。8:4表達了AB與CD的份數關系，以CD為標準去度量AB,可以量2次，也就是2倍，標準作后項，被度量對象作前項。按照“AB是CD的2倍”說法，說一說對CD是AB的的理解。

第二組：根據題目提供的條件能寫出比嗎？

①我們班男生有25人，女生有24人。

②新冠疫情期間，學校常用84消毒液對校園消毒，按要求：1000ml水加84消毒液10ml。

③行15km，需要3時。

④在一杯糖水中，有蔗糖10g,水100g。

⑤某商場規定：每買5支牙膏送2把牙刷。

⑥買3kg蘋果，需要人民幣42元。

第三組：下面哪些說法是正確的？哪些是錯誤的？簡要說明理由。

②游艇上有12人，平均身高157cm,身高與人數的比為157:12。

③蝸牛2h全速爬行的路程是17m，路程與時間之比是17：2。

④混凝土由水、沙、碎石組成，在某一時刻的比是4:2:3。

⑤紅、藍兩隊進行籃球比賽，比分16:8。

⑥笑笑身高1.4m,媽媽身高165cm，笑笑與媽媽身高的比1.4:165。

上述教學材料以學生已有（生活、認知）經驗為切入點和突破口，體現了比產生的歷史邏輯，突出了比的理論邏輯，反映了對改善發展學生數學思維的價值。學生在數學學習活動中，通過對第一組教學材料的探索、猜想、論證與辨析，理解比產生的根本原因是兩個同類量的比較，體會比產生的必要性；比是兩個同類量的倍數關系，是用單位標準去度量另一個同類量的表達；把握比各部分名稱及求比值，單位標準作后項，另一個同類量作前項，理解比、除法、分數之間的關系。通過對第二組教學材料的分析、判斷、比較、分類，在矛盾與反轉、思考與辨析中溝通與兩個同類量比的聯系，將兩個同類量比的意義遷移到不同類量，理解單位標準度量另一個不同類量，產生新“量”，重構出不同類量的比是倍數關系的表達或度量，打通比、除法、分數之間的內在聯系。通過對第三組材料具體實例的分析、比較，辨析除法、比，深度理解比的數學本質是兩個數量之間倍數關系的表達或度量，不是除法運算；幫助學生建立起如圖8的關系結構。

概而言之，基于數學是一種創造性活動的小學數學教學材料設計，需要精準把握教學內容的歷史邏輯、理論邏輯、價值邏輯和實踐路徑。這樣，學生學習數學時才能思維、情感、理智、價值態度等全身心投入，在簡略經歷數學知識的歷史演變過程中，理解數學知識的本質，建立數學關系結構，感悟數學基本思想，改善發展數學思維，提升數學思維品質。