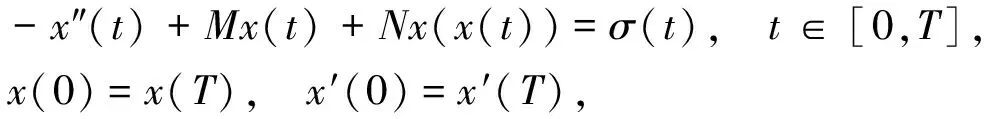一類二階迭代微分方程周期問題解的存在性

康 慧 君

(西北師范大學 數學與統計學院, 蘭州 730070)

0 引 言

迭代微分方程是一類泛函微分方程, 有很強的實際應用背景, 目前已得到廣泛關注[1-16]. 例如: 古典的Euler幾何問題可導出方程

x(t)x′(t)=x(c+x(t));

Poisson幾何問題可導出方程

x(x(t))+x(x(t))x′(x′(t))-x(x(t+x(t)x′(t)))=1.

Cooke[1]提出了生物學中的重要方程

x′(t)+ax(t-h(t,x(t)))=F(t),

該方程與遺傳現象有關. 此外, 迭代微分方程在人口模型[2]、 日用品的價格波動模型[3]和血細胞的生產模型[4]中均有重要應用. 特別地, Eder[5]用壓縮映射原理討論了一階迭代微分方程

x′(t)=x(x(t)),x(t0)=t0,t0∈[-1,1]

x′(t)=f(x(x(t))),x(0)=0

局部解的存在性. Kaufmann[7]用Schauder不動點定理研究了二階迭代微分方程

x″(t)=f(t,x(t),x(x(t)),t∈[a,b]

(1)

在滿足如下邊界條件之一下解的存在唯一性:

x(a)=a,x(b)=b;

(2)

x(a)=b,x(b)=a.

(3)

其中f: [a,b]××→是連續函數.

設f滿足如下條件:

(H1) 存在常數K,L>0, 使得

(H2) 存在M,N>0, 使得

|f(t,u1,v1)-f(t,u2,v2)|≤M|u1-u2|+N|v1-v2|,t∈[a,b],u1,u2,v1,v2∈.

文獻[7]得到如下結果:

定理1[7]若f滿足條件(H1), 則問題(1)-(2)或問題(1)-(3)存在解, 若f滿足條件(H2), 則問題(1)-(2)或問題(1)-(3)存在唯一解.

上述結論是在f有界情形下考慮解的存在唯一性, 本文考慮當f無界時, 二階迭代微分方程周期邊值問題是否也可建立解的存在唯一性結果, 即考慮一類二階迭代微分方程周期邊值問題

(4)

解的存在性.

本文總假設:

(H3)f: [0,T]×2→是連續函數.

1 引 理

下面用極大值原理說明單調迭代方法的正確性.

引理1設x∈E=C([0,T],)∩C2([0,T],), 若存在M>0,N>0, 使得下列條件成立：

1) -x″(t)+Mx(t)+Nx(x(t))≥0,t∈[0,T];

2)x(0)=x(T),x′(0)≤x′(T);

則?t∈[0,T],x(t)≥0.

證明: 反設x(t)<0,t∈[0,T].考慮如下兩種情形.

情形1) 設x(t)≤0,x(t)不恒為0,t∈[0,T].在該情形下, 可得x(0)=x(T),x′(0)≤x′(T),x″(t)≤0,t∈[0,T], 因此在區間[0,T]上x(t)=K<0, 其中K是常數.從而

0≤-x″(t)+Mx(t)+Nx(x(t))=(M+N)K,

與K<0矛盾.

情形2) 存在t1,t2∈[0,T], 使得x(t1)>0,x(t2)<0.此時, 又有如下兩種情形.

①x(0)=x(T)>0.此時, 存在t3∈(0,T), 使得

x″(t)≤(M+N)x(ξ),t∈[0,t3).

(5)

對式(5)兩邊從s(ξ

-x′(s)≤(t3-s)(M+N)x(ξ),

(6)

x″(t)≤(M+N)x(ξ),t∈[0,T].

(7)

當ξ>t3時, 對式(7)兩邊從t3(t3

x′(s)≤(s-t3)(M+N)x(ξ),

(8)

引理2設x∈E=C([0,T],)∩C2([0,T],), 若存在M>0,N>0, 使得下列條件成立：

1) -x″(t)+Mx(t)+Nx(x(t))≥0,t∈[0,T];

2)x(0)=x(T),x′(0)≤x′(T)；

則?t∈[0,T],x(t)≥0.

證明: 反設x(t)<0,t∈[0,T].考慮如下兩種情形.

情形1) 設x(t)≤0,x(t)不恒為0,t∈[0,T].證明如引理1中情形1)的證明, 故略.

情形2) 存在t1,t2∈[0,T], 使得x(t1)>0,x(t2)<0.此時, 又有如下兩種情形.

①x(0)=x(T)>0.此時, 存在t3∈(0,T), 使得

-x″(t)+Mx(t)≥-Nx(ξ),t∈[0,t3).

x′(t)=emt(v′(t)+mv(t)),x″(t)=emt(v″(t)+2mv′(t)+m2v(t)).

因此-v″(t)-2mv′(t)≥-Ne-mtx(ξ),t∈[0,t3), 即

(e2mtv′(t))′≤Nemtx(ξ),t∈[0,t3).

(9)

對式(9)兩邊從s(ξ

v′(t3)=e-mt3x′(t3)-mv(t3)=-mv(t3)>0,

可得

即

(10)

對式(10)兩邊從ξ到t3積分, 得

即

而

從而

與條件3)矛盾.

②x(0)=x(T)≤0.此時, 存在t3∈[0,T], 使得

-x″(t)+Mx(t)≥Nx(ξ),t∈[0,T].

當ξ

(e2mtv′(t))′≤Nemtx(ξ),t∈[0,T].

(11)

對式(11)兩邊從t3(t3

即

(12)

對式(12)兩邊從t3到ξ積分, 得

即

而

從而

與條件3)矛盾.證畢.

2 主要結果

為在問題(4)中利用單調迭代方法, 考慮如下線性周期邊值問題：

(13)

其中σ∈C([0,T],).

若存在α∈E滿足

則α稱為問題(13)的一個下解； 反之, 若存在β∈E滿足

則β稱為問題(13)的一個上解.

對于α,β∈E, 如果α(t)≤β(t),t∈[0,T], 則有如下表示:

[α,β]={x∈E:α≤x≤β}.

定理2假設問題(13)存在一個下解α和一個上解β, 滿足α≤β, 且引理1中條件3)成立, 則問題(13)有唯一解x∈[α,β].

證明: 考慮周期邊值問題

(14)

其中

易驗證p: [0,T]×→是連續的.

定義算子Φ:E→E為

(15)

其中

m=M1/2.則算子Φ:E→E是全連續算子.

由于-Np(t,x(x(t)))+σ(t)在[0,T]上有界, 則Φ在E上也有界.根據Schauder不動點定理知, 存在算子Φ的一個不動點x, 使得x∈E是問題(14)的一個解.

下面證明x∈[α,β].首先證明x≥α.設u(t)=x(t)-α(t).由于p(t,x(x(t)))-α(x(t))≤max{u(x(t)),0},t∈[0,T], 則由下解的定義可得:

(i) -u″(t)+Mu(t)+Nmax{u(x(t)),0}≥0,t∈[0,T];

(ii)x(0)=x(T),x′(0)≤x′(T);

反設x(t)<α(t),t∈[0,T].考慮如下兩種情形.

情形1) 設u(t)≤0,u(t)不恒為0,t∈[0,T].此時可得u(0)=u(T),u(0)′≤u′(T),u″(t)≤0,t∈[0,T], 因此在區間[0,T]上u(t)=K<0, 其中K是常數.從而

0≤-u″(t)+Mu(t)+Nmax{u(x(t)),0}=MK,

與K<0矛盾.

情形2) 存在t1,t2∈[0,T], 使得u(t1)>0,u(t2)<0.此時, 又有如下兩種情形.

u″(t)≤(M+N)u(ξ),t∈[0,t3).

u″(t)≤(M+N)u(ξ),t∈[0,T].

若存在α∈E滿足

則α稱為問題(4)的一個下解； 反之, 若存在β∈E滿足

則β稱為問題(4)的一個上解.

定理3假設存在問題(4)的一個上解α和一個下解β, 使得在[0,T]上α≤β.并存在常數M>0,N>0, 滿足下列條件：

1)f(t,u2,v2)-f(t,u1,v1)≥-M(u2-u1)-N(v2-v1),t∈[0,T],α(t)≤u1≤u2≤β(t),α(x(t))≤v1≤v2≤β(x(t));

則存在序列{αn}非減、 {βn}非增, 使得其在[α,β]上單調一致收斂于問題(4)的極值解, 其中α0=α,β0=β.

證明: 對于η∈[α,β], 考慮如下問題：

σ(t)=ση(t)=f(t,η(t),η(x(t)))+Mη(t)+Nη(x(t)).

(16)

由于η∈[α,β], 由條件1)和上下解的定義知

-β″(t)+Mβ(t)+Nβ(x(t))≥ση(t).

因此,α和β分別是問題(16)的一個上解和下解.根據定理2, 定義算子A: [α,β]→[α,β],Aη是問題(16)的唯一解.由引理1可知A是[α,β]上的單調增算子, 即η1,η2∈[α,β],η1≤η2,Aη1≤Aη2.

定義序列{αn},{βn}, 其中αn+1=Aαn,βn+1=Aβn,α0=α,β0=β.則有

α0=α≤α1≤…≤αn≤βn≤…≤β0=β.

在[0,T]上單調一致有界, 從而α*(t),β*(t)是問題(4)的解.

進一步, 若x∈[α,β]是問題式(4)的解, 則由歸納法可知,αn(t)≤x(t)≤βn(t),t∈[0,T],n=0,1,2,…, 因此x∈[α*,β*].于是α*(t),β*(t)分別是問題(4)在[α,β]上的極小值解和極大值解.證畢.