對稱思想在初中數(shù)學(xué)教學(xué)中的應(yīng)用
——以“代數(shù)中的對稱思想”為例

?山東省青島市嶗山區(qū)育才學(xué)校 張 珺

1 數(shù)與代數(shù)中的對稱

進(jìn)入初中之后，學(xué)生所遇到的第一個(gè)門檻就是負(fù)數(shù)，負(fù)數(shù)不僅是后續(xù)知識的重要基礎(chǔ)，也是生活中的一個(gè)重要工具.對于“正負(fù)術(shù)”，世界上最早的記載在《九章算術(shù)》中，我國古代著名數(shù)學(xué)家劉徽說：“今兩算得失相反，要令正負(fù)以名之，正算赤，負(fù)算黑，否則以邪正為異.”可見對稱的思想在古代數(shù)學(xué)研究中就占據(jù)重要位置，這一對量，單看并沒有實(shí)際意義，正是有了“-”才有“+”一說.關(guān)于相反數(shù)和絕對值，《義務(wù)教育教學(xué)課程標(biāo)準(zhǔn)(2011年版)》中要求能夠借助數(shù)軸明確它們的概念及意義，結(jié)合對稱思想，讓學(xué)生更能直觀地感受到相反數(shù)是成對存在的.

從形式上看，平方差公式(a+b)(a-b)=a2-b2，完全平方公式(a+b)2=a2+2ab+b2，都具有簡潔美、和諧美，無論是等式的左邊還是右邊，形式也是對稱的.教材“讀一讀”中，引入了數(shù)學(xué)史——楊輝三角(如圖1)，鼓勵(lì)學(xué)生經(jīng)歷探索公式的過程，激發(fā)學(xué)習(xí)數(shù)學(xué)的興趣.

圖1

楊輝三角就像金字塔一樣，可以看作一個(gè)等腰三角形，我們發(fā)現(xiàn)以等腰三角形底邊上的高為對稱軸，左、右側(cè)的數(shù)是對稱分布的.其實(shí)只要學(xué)生懂得原理和涵義，就可以直接根據(jù)楊輝三角得到(a+b)n(n是正整數(shù))的二項(xiàng)展開式中的各項(xiàng).

2 對稱思想的應(yīng)用

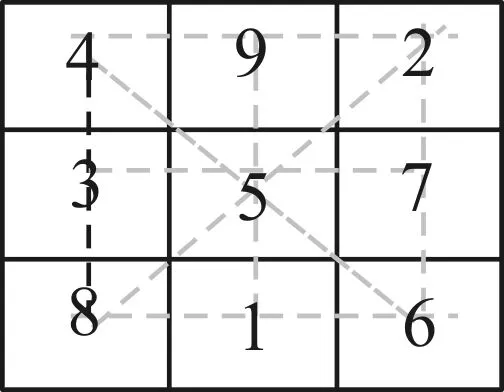
圖2

例1課例“探尋神奇的幻方”，在圖2所示的三階幻方中，請思考：

(1)你發(fā)現(xiàn)了哪些相等的關(guān)系？各行、各列、各對角線上的數(shù)之和是多少？

(2)若是將和相等的每一組數(shù)連線，你有什么發(fā)現(xiàn)？

(3)你能變換數(shù)的位置，使新得到的九宮格仍然滿足上述你的發(fā)現(xiàn)嗎？

(4)幻方中，最核心位置是什么？有沒有“成對”的數(shù)？

2.1 觀察研究

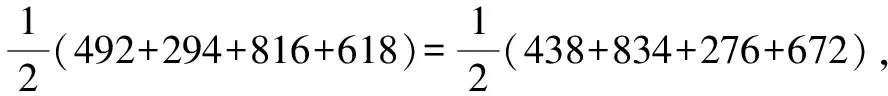
如圖2所示，各行、各列、各對角線上的三個(gè)數(shù)之和都為15，5在中間，可以看作“對稱中心”，偶數(shù)在四個(gè)角中，并且每對數(shù)之和都為10，其余是奇數(shù)，也是成對存在且和為10.

2.2 創(chuàng)新構(gòu)造

引導(dǎo)學(xué)生自己構(gòu)造出三階幻方，并提問：

(1)幻方中，最核心位置是什么？有沒有“成對”的數(shù)？

(2)5為什么必須放到正中間？

(3)4個(gè)角上可以放奇數(shù)嗎？

(4)若設(shè)中間數(shù)為x，你能得到關(guān)于x的哪些式子？

(5)還有什么新發(fā)現(xiàn)嗎？

分析：要構(gòu)造一個(gè)新的幻方，方法不是唯一的.經(jīng)過上面一系列問題的鋪墊，我們已經(jīng)發(fā)現(xiàn)5的位置是固定在最中間的，對于“為何必須5放中間”這一問題，要使每條線上三個(gè)數(shù)之和都為15，在1～9這九個(gè)數(shù)中，只有5沒有“對”，剩下的八個(gè)數(shù)都可以兩兩為一對，和為10，因此，核心位置只能填5.而剩下位置的填寫，只要讓八個(gè)數(shù)成對存在即可，1和9，2和8，3和7，4和6，只要確定其一，那么對稱的位置就是另一個(gè)數(shù).此外，我們發(fā)現(xiàn)要構(gòu)成新的幻方，四角處必須放偶數(shù)，這可以用奇偶性來解釋.奇數(shù)+奇數(shù)=偶數(shù)，奇數(shù)+偶數(shù)=奇數(shù)，偶數(shù)+偶數(shù)=偶數(shù)，而5又在中間，如果此時(shí)四個(gè)角上是奇數(shù)，剩余四格放偶數(shù)，那么第一、三行，第一、三列的和都是偶數(shù)，這與題意不符，如圖3-1所示.如果四個(gè)角上是一奇一偶，第一、三行的和一定是偶數(shù)，也不符合題意，如圖3-2所示.如果四個(gè)角上都填偶數(shù)呢？此時(shí)，九宮格中的每一橫行、每一豎行，還有兩條對角線上的數(shù)之和一定是奇數(shù)，保持了結(jié)果奇偶性的一致性，符合題意，如圖3-3所示.經(jīng)過分析，不難發(fā)現(xiàn)，當(dāng)數(shù)為1到9這九個(gè)數(shù)時(shí)，只有當(dāng)九宮格的四個(gè)角處的數(shù)是偶數(shù)，5放在中間，其余各個(gè)奇數(shù)放到剩余位置時(shí)，才能滿足幻方的要求.

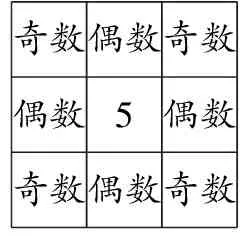
奇數(shù)偶數(shù)奇數(shù)偶數(shù)5偶數(shù)奇數(shù)偶數(shù)奇數(shù)

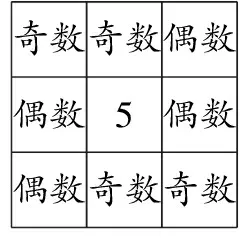
奇數(shù)奇數(shù)偶數(shù)偶數(shù)5偶數(shù)偶數(shù)奇數(shù)奇數(shù)

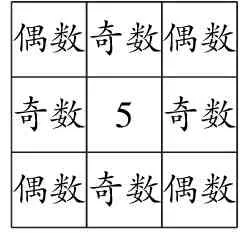
偶數(shù)奇數(shù)偶數(shù)奇數(shù)5奇數(shù)偶數(shù)奇數(shù)偶數(shù)

對于“成對”出現(xiàn)的數(shù)，可以引導(dǎo)學(xué)生利用對稱來構(gòu)造幻方，先確定中間的數(shù)，其余各數(shù)根據(jù)對稱成對地分布，并根據(jù)橫行、豎列的奇偶性確定數(shù)的位置.通過美妙地變換，幫助學(xué)生在動(dòng)手實(shí)踐的過程中，形成對幻方的感性認(rèn)識，感受數(shù)學(xué)的對稱美.

無論是哪種幻方，它們都有共同的性質(zhì)：各行、各列、各對角線的數(shù)之和都為同一常數(shù)；在同行、同列或同對角線上關(guān)于中心數(shù)對稱的兩個(gè)數(shù)之和，是中心數(shù)的兩倍；幻方中的每一個(gè)數(shù)同時(shí)加上或者同時(shí)乘一個(gè)常數(shù)，可以得到一個(gè)新的幻方；把以中心所在直線為對稱軸分布的兩行或兩列數(shù)交換，仍可得到一個(gè)幻方.

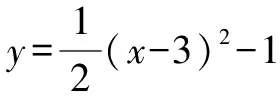
(1)求點(diǎn)A，B，D的坐標(biāo)；

(2)連接CD，過點(diǎn)O作OE⊥CD，垂足為H，OE與拋物線的對稱軸交于點(diǎn)E，連接AE，AD，求證：∠AEO=∠ADC；

(3)在(2)的條件下，以點(diǎn)E為圓心，1為半徑畫圓，在對稱軸右側(cè)拋物線上有一動(dòng)點(diǎn)P，過點(diǎn)P作⊙E的切線，切點(diǎn)為Q，當(dāng)PQ的長為最小時(shí)，求點(diǎn)P的坐標(biāo)，并寫出點(diǎn)Q的坐標(biāo).

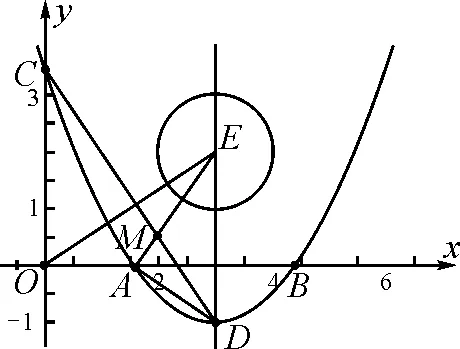
圖4

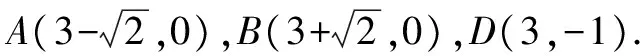
(2)點(diǎn)E的坐標(biāo)為(3，2).則AE2=6，AD2=3，DE2=9，則AE2+AD2=DE2，所以∠EAD=90°.設(shè)AE交CD于點(diǎn)M，又因?yàn)镺E⊥CD，且∠CME=∠AMD，所以可得，∠AEO=∠ADC.

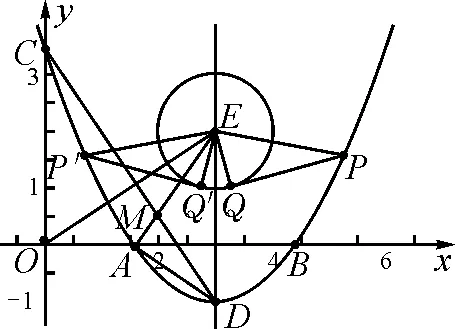
圖5

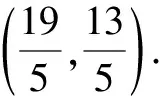
3 思考與建議

關(guān)于如何在課堂教學(xué)中滲透對稱思想，本研究認(rèn)為教學(xué)過程中可以從以下角度改進(jìn).

3.1 了解對稱思想的背景知識

準(zhǔn)確應(yīng)用對稱思想的前提是了解對稱思想，只有清楚對稱思想的背景，才能正確把握對稱思想的涵義，這又為我們提供了發(fā)現(xiàn)數(shù)學(xué)規(guī)律的一把鑰匙，同時(shí)要求教師要有精準(zhǔn)的專業(yè)學(xué)科知識，不斷擴(kuò)充認(rèn)知，常言道“要給學(xué)生一杯水，老師要有常流水”，這是其一；其二，要引導(dǎo)學(xué)生重視思想方法的背景，如洛書河圖就是一個(gè)很好的起點(diǎn)，通過歷史文化的力量增強(qiáng)學(xué)生學(xué)習(xí)的內(nèi)在思想動(dòng)機(jī)，從深層次理解對稱思想，而不是簡簡單單地將其劃分為軸對稱和中心對稱.這種關(guān)于數(shù)學(xué)思想的學(xué)習(xí)是有意義的學(xué)習(xí)，數(shù)學(xué)的發(fā)展并不是題目的完成是否正確，而是在數(shù)學(xué)思想的指導(dǎo)下創(chuàng)造、生長出新知識.

3.2 挖掘教材中的對稱思想

“對稱”既然被稱為“思想”，那它的本質(zhì)是隱性的知識，這也決定了對稱思想的抽象性.例如，在幾何中，我們常會(huì)借助對稱思想研究矩形的性質(zhì)，教師應(yīng)當(dāng)向?qū)W生強(qiáng)調(diào)這種思想的優(yōu)越性，引起學(xué)生對對稱思想的重視，引導(dǎo)學(xué)生有意識地利用對稱思想進(jìn)行幾何圖形的探究.對正方形、菱形等圖形的探究，可以不斷強(qiáng)化學(xué)生運(yùn)用對稱思想研究圖形性質(zhì)，幫助學(xué)生將抽象的數(shù)學(xué)思想內(nèi)化成有力的探究工具，對對稱思想不斷形成更深刻的理解.

3.3 層層推進(jìn)對稱思想

數(shù)學(xué)的學(xué)習(xí)是一個(gè)漫長的發(fā)展過程，在這個(gè)過程中，教師應(yīng)當(dāng)有計(jì)劃、有層次地推進(jìn)思想教學(xué).教師要遵循學(xué)生的身心發(fā)展規(guī)律，不能陵節(jié)而施，要做到循序漸進(jìn).當(dāng)學(xué)生處于知識的形成階段時(shí)，教師可以從簡單的層次說明對稱思想，當(dāng)學(xué)生處于知識的運(yùn)用階段時(shí)，就可以像爬梯子一樣以更高的層次再次詮釋、補(bǔ)充對稱思想了.

總之，由于學(xué)生的認(rèn)知特點(diǎn)，教師在教學(xué)過程中，應(yīng)當(dāng)遵循學(xué)生的認(rèn)知規(guī)律，以螺旋式結(jié)構(gòu)不斷提升學(xué)生對于對稱思想的認(rèn)識、掌握及應(yīng)用，為學(xué)生提供探索數(shù)學(xué)的機(jī)會(huì)，引導(dǎo)學(xué)生跨越最近發(fā)展區(qū)，最終實(shí)現(xiàn)學(xué)生數(shù)學(xué)素養(yǎng)的整體提升.F