一類泛函極小值點的幾何刻畫

薛 榮

(中國人民銀行蘭州中心支行 國際收支處，甘肅 蘭州 730000)

0 引言

變分理論旨在研究泛函的極大值和極小值問題，它的解法非常類似于數(shù)學(xué)分析中函數(shù)的極大值和極小值的方法.變分在泛函的研究中所起的作用，如同微分在函數(shù)的研究中所起的作用.這里先對變分的概念作以扼要陳述.

Δf=
f[y(x)+αδy]-f[y(x)]=
L[y，αδy]+β(y，αδy)|α|max|δy|.

f[y+αδy]對α的導(dǎo)函數(shù)于α=0時的值等于

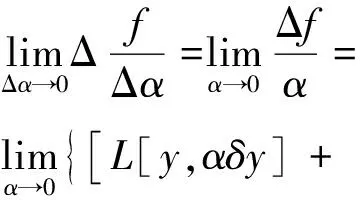
因此

如果Δf=f[y(x)]-f[y0(x)]≤0(≥0)，則說泛函f[y(x)]在y=y0(x)上達到極大值(極小值).如果Δf≤0(≥0)，而只在y=y0(x)時才有Δf=0，則說泛函f[y(x)]在y=y0(x)上達到嚴格的極大值(極小值)[1-3].

本文就復(fù)Hilbert空間中共軛雙線性Hermite泛函的極小值和相應(yīng)的變分不等式作一些討論.

1 預(yù)備知識

(1)φ(αx+βy，z)=αφ(x，z)+βφ(y，z);

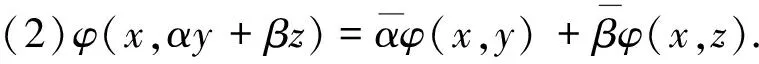
定義2[5]設(shè)φ(·，·)是線性空間X上的一個共軛雙線性泛函，如果存在M>0，使得

|φ(x，y)|≤M‖x‖‖y‖(?x，y∈X)，

則稱φ(·，·)是X上的有界共軛雙線性泛函.當φ(·，·)是X上的有界共軛雙線性泛函時，記

稱‖φ‖是泛函φ(·，·)的范數(shù).

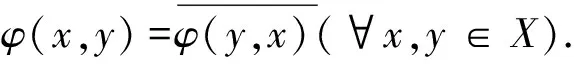
引理1設(shè)φ(·，·)是內(nèi)積空間X上的共軛雙線性泛函，則φ(·，·)是有界的?φ(·，·)是二元連續(xù)的.

證明設(shè)φ(·，·)在X上有界，并設(shè)xn，x，yn，y∈X(n=1，2，…)，xn→x，yn→y.由于

|φ(xn，yn)-φ(x，y)|≤
|φ(xn，yn)-φ(xn，y)|+
|φ(xn，y)-φ(x，y)|≤
‖φ‖(‖xn‖‖yn-y‖+
‖xn-x‖‖y‖)→0(n→+∞)，

所以，φ(·，·)是二元連續(xù)函數(shù).

反之，設(shè)φ(·，·)是二元連續(xù)函數(shù)，如果φ(·，·)不是有界的，即存在{xn}，{yn}?X，‖xn‖=1，‖yn‖=1，使得

|φ(xn，yn)|≥n3(n=1，2，…).

顯然

又因為φ(·，·)是雙線性泛函，易知φ(0，y)=φ(x，0)=φ(0，0)=0 (?x，y∈X)，從而由上式得到

這與φ(·，·)是二元連續(xù)函數(shù)的假設(shè)矛盾.所以φ(·，·)是有界的.證畢.

引理2[4-5](變分引理) 設(shè)X是Hilbert空間，M是X的一個非空閉凸子集，則?x∈X，?|y0∈M，使得

2 主要結(jié)果

定理1[6]設(shè)X是復(fù)Hilbert空間，φ(x，y)是X上的共軛雙線性Hermite泛函，并且?M>0，δ>0，使得

δ‖x‖2≤φ(x，x)≤

M‖x‖2(?x∈X).

又設(shè)u0∈X，E是X中的一個閉凸子集，則函數(shù)

x|→φ(x，x)-Re(u0，x) (x∈X)

在E上達到最小值，并且達到最小值的點x0滿足變分不等式

Re[2φ(x0，x-x0)-(u0，x-x0)]≥
0 (?x∈E).

證明(1)先證φ(·，·)是X上的有界共軛雙線性泛函，并且‖φ‖≤M.

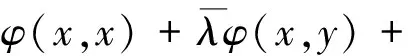
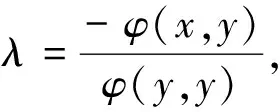
從而

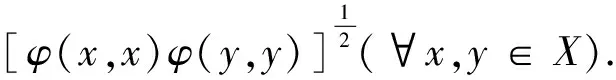
再由題設(shè)給出的不等式得，

|φ(x，y)|≤M‖x‖‖y‖(?x，y∈X).

因此，φ(·，·)是X上的有界共軛雙線性泛函，并且‖φ‖≤M.

(2)證明定理1.記f(x)=φ(x，x)-Re(u0，x)(x∈X).根據(jù)引理1，φ(·，·)是X上的二元連續(xù)線性泛函.又容易驗證Re(u0，x)是X上的實值連續(xù)線性泛函，所以f(x)是X上的實值連續(xù)線性泛函.注意到線性連續(xù)和線性有界等價，因此，f(x)在X上有界，從而有下確界.由于E是Hilbert空間X中的閉凸子集，據(jù)引理2(變分引理)，?x∈X，?|x0∈E，使得

于是

|f(x)-f(x0)|=|f(x-x0)|≤
‖f‖‖x-x0‖=‖f‖ρ(x，E) (?x∈X).

下證變分不等式.記Δx=x-x0(x，x0∈E).設(shè)t∈(0，1)，則x0+tΔx=tx+(1-t)x0∈E，從而

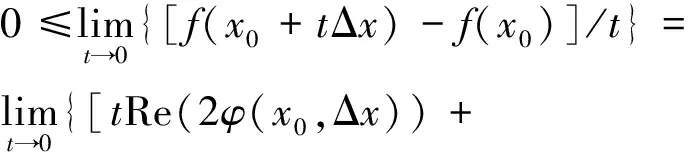
證畢.

定理2設(shè)X是復(fù)Hilbert空間，ψ是X上的線性連續(xù)泛函，M是X中的一個閉凸子集，則?u0∈X，使得函數(shù)

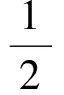
在M上有最小值，并且達到最小值的點x0滿足變分不等式

Re[(x0，x-x0)-(u0，x-x0)]≥
0 (?x∈M).

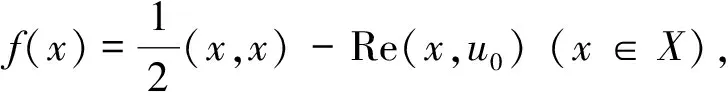
從而

|f(x)-f(x0)|=|f(x-x0)|≤
‖f‖‖x-x0‖=
‖f‖ρ(x，M) (?x∈X).

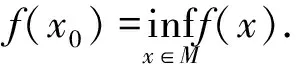
下證變分不等式.記Δx=x-x0(x，x0∈M)，并設(shè)t∈(0，1)，則x0+tΔx=tx+(1-t)x0∈M，從而

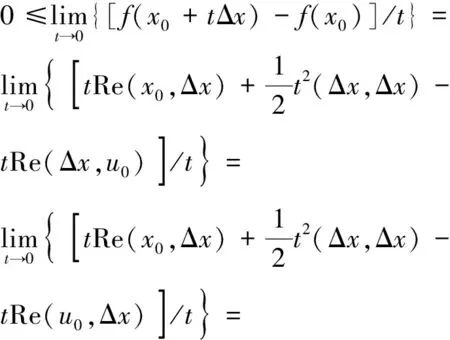
證畢.

定義4設(shè)φ(·，·)是線性空間X上的一個共軛雙線性泛函，稱由

q(x)?φ(x，x) (?x∈X)

定義的函數(shù)q(x)為X上由φ誘導(dǎo)的二次型.

引理3設(shè)φ(·，· )是線性空間X上的共軛雙線性泛函，q是由φ誘導(dǎo)的二次型,則

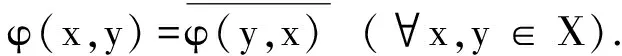
證明“?”是顯然的.下證“?”.由于

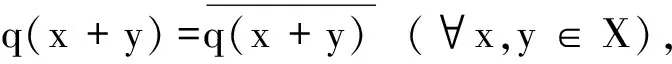
從而

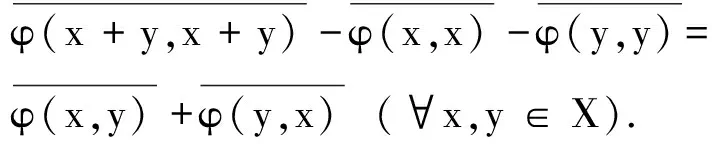
即得

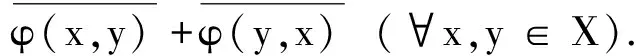
(1)

把式(1)中的y換成iy，

左右兩端同除以i,得

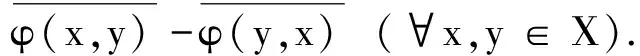
(2)

式(1)與式(2)相減,即得

證畢.

定理3設(shè)X是復(fù)Hilbert空間，A為X的非空閉凸子集，f∈X*，φ(·，·)為X上的有界共軛雙線性Hermite泛函,則?|x0∈A，使得函數(shù)

x|→φ(x，x)-Ref(x) (?x∈X)

在A上達到最小值，并且達到最小值的點x0滿足變分不等式

Re[2φ(x0，x-x0)-f(x-x0)]≥
0 (?x∈A).

證明記ψ(x)=φ(x，x)-Ref(x) (?x∈X).由題設(shè)，φ(·，·)是X上的共軛雙線性Hermite泛函，據(jù)引理3，φ(x，x)∈R(?x∈X).又由題設(shè)，φ(·，·)在X上是有界的，據(jù)引理1，φ(·，·)是X上的二元連續(xù)泛函.又據(jù)題設(shè)，f∈X*，因此，ψ(x)是X上的實值連續(xù)線性泛函.由于線性泛函的連續(xù)性和有界性等價，所以，ψ(x)在X上有界，從而有下確界.據(jù)題設(shè)，A是Hilbert空間X中的非空閉凸子集，據(jù)引理2 (變分引理)，?x∈X，?|x0∈A，使得

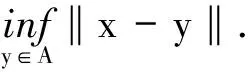
于是

|ψ(x)-ψ(x0)|=
|ψ(x-x0)|≤‖ψ‖‖x-x0‖=
‖ψ‖ρ(x，A) (?x∈X).

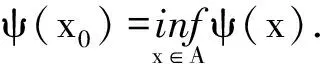
下證變分不等式.記Δx=x-x0(x，x0∈A)，設(shè)t∈(0，1)，則x0+tΔx=tx+(1-t)x0∈A，從而

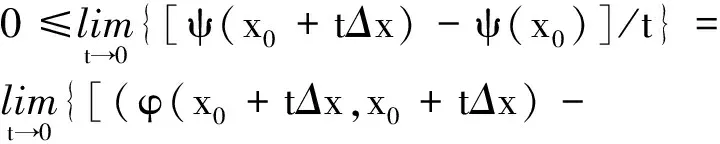
證畢.

3 結(jié)語

本文使用初等方法討論了與復(fù)Hilbert空間中范數(shù)相關(guān)的泛函的極小值的存在性，并對極小子給出了幾何刻畫.定理1討論的是一個經(jīng)典的泛函極小值和與之相關(guān)的變分不等式，但筆者沒有看見過它的證明，故在此給出了一個較為初等的證明.