考慮時延速度差和限速信息的智能網聯車跟馳模型

張凱望，惠飛，張國祥，石琦，劉志忠

（1.長安大學信息工程學院，西安 710064；2.河北省高速公路集團有限公司延崇籌建處，河北張家口 075400）

0 引言

伴隨著車聯網（Internet of Vehicles，IoV）技術的不斷發展，駕駛員可以通過車載終端有效地獲取越來越多的車輛信息和道路信息，從而優化駕駛動作，從微觀交通流層面改善交通的運行質量［1］。微觀交通流的主要研究方向智能網聯車跟馳模型可以為未來大規模實施自動駕駛的實地測試提供模型參照，已經成為當前車聯網技術和智慧交通領域的研究熱點［2］。

早在20 世紀，Bando 等［3］通過對車輛跟馳行為的研究，提出OV（Optimal Velocity）跟馳模型，可以用來描述多種現實生活中的交通行為（如：走走停停、交通阻塞、交通順暢等），但是該模型具有不切合實際的加速度和減速度，這部分內容和實際相差過大。Jiang 等［4］根據OV 模型存在的問題，提出了FVD（Full Velocity Difference）模型，該模型考慮了在跟馳車流中，速度差信息對穩定性的影響，更加全面地描述了車輛的跟馳行為。近幾年，人們對跟馳模型進行了更加深入的研究，不斷改進FVD 模型使之盡可能貼近現實［5-13］。早在1958 年，時延就被認為是交通研究中一個重要的影響參數，它主要來源于駕駛員感知周圍環境變化而采取相應行動所需要以及車輛根據駕駛員做出行為而完成動作的時間，其主要受駕駛員自身狀況、周圍環境以及車輛特征的影響［14-16］。由于時延對交通流有著重大影響，因此，有必要對交通流中的時延問題進行更深入的研究。Orosz 等［17-18］討論了以車輛驅動時延為特征的OV 模型的局部和全局穩定性；Yu 等［19］研究了OV 模型的密度波；Zhou 等［20］提出了最優速度差模型（Optimal Velocity Difference Model，OVDM），該模型考慮了車輛驅動的反應時間延遲；Jia 等［21］研究了考慮了車輛之間的時延以及駕駛員感知時延信息對交通流的影響；Zhang 等［22］研究了由于駕駛員反應性時間延遲效應造成的時滯速度差對車輛加速度的影響；Ma 等［23］提出了考慮時延速度差的跟馳模型。但是這些模型都沒有考慮到在當前的車聯網環境下，不僅可以通過分析獲得時延速度差，也可以輕松獲得道路的限速信息，駕駛員可以通過對這些信息，及時對車輛駕駛進行調整，從而有利于提高跟馳車流的穩定性。

本文提出了一種基于智能網聯車的跟馳模型——考慮時延速度差和限速信息的跟馳模型TD-VDVL（Time-Delayed Velocity Difference and Velocity Limit）。為了驗證TD-VDVL模型的穩定性，首先，通過線性譜波微擾法對模型進行線性穩定性分析；然后，分析模型中各個參數對跟馳系統穩定性的影響；最后，使用Matlab 數值仿真平臺，對模型進行數值模擬和仿真實驗。實驗結果表明改進模型對于穩定道路交通流具有一定的優越性。

1 TD-VDVL模型建立

駕駛員在跟馳駕駛過程中，可以根據道路環境和車輛情況作出相應的駕駛決策，從而影響整個跟馳車隊的穩定性。Jiang 等［4］為了更好地描述這種跟馳行為，提出了FVD 模型。

FVD 模型的車輛運動方程展開式為：

其中：a表示最優速度敏感系數，V(Δyi)表示最優速度函數，λ表示速度差反應系數。

該模型沒有考慮到在現有的駕駛環境下，駕駛員可以通過智能網聯汽車獲取當前道路的限速信息［24］以及時延造成的速度差信息，這些都將對駕駛員的駕駛決策產生影響，從而影響整個交通系統的穩定性。因此引入時延速度差信息和限速信息對FVD 模型進行改進。

改進后的模型為：

對其進行展開描述為：

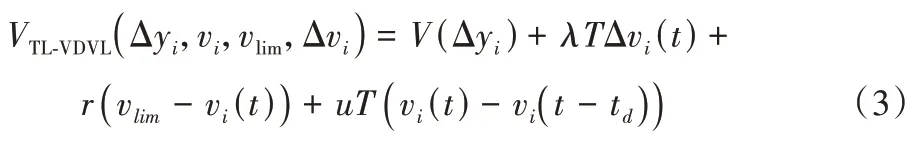
其中：t表示當前時刻；v表示t時刻車速；λ表示速度差的反應系數；Δyi(t) 表示前后車車頭之間的間距，Δyi(t)=yi+1(t) -yi(t)；Δvi(t) 表示前后 車的速度 差，Δvi(t)=vi+1(t) -vi(t)；V(·)表示跟馳車的最優速度函數；T表示駕駛員感知周圍環境的時間；γ表示限速信息的敏感系數；td表示時延；vi(t) -vi(t-td)表示時延造成的速度差；u表示對vi(t) -vi(t-td)的敏感系數。

本文使用的最優速度函數V(Δyi)［25］如下：

為了更加清楚地反映跟馳車流的穩定性，參照文獻［26］，對T進行簡化，過程如下：

將式（5）代入式（3）中得：

2 穩定性分析

根據參考文獻［27］，使用線性譜波微擾法對TD-VDVL模型進行線性穩定性分析，即對處于同質均衡狀態的跟馳車流（即道路上行駛的車輛全部使用同一種跟馳模型，并且沒有發生換道行為以及行人等其他交通單元的干擾），改變其中某一個車輛的位置，使之稍微偏離其處于穩定狀態時的位置。若在該干擾下，跟馳車隊的車頭間距或者車隊速度沒有較大變化，則認為交通流是穩定的［28］。

故有：

泰勒展開式為：

對V(Δyi(t))和vi(t)分別進行泰勒展開并忽略非線性項的影響得到：

聯立式（12）、（13），可得：

為了便于穩定性分析和計算，這里取vlim=V(h)，將式（12）～（14）代入式（6）中得到關于xi(t)的微分方程：

將式（16）代入式（15）并化簡可得：對ejk和e-ztd進行泰勒展開，并將參數z展開為z=z1(jk) +z2(jk)2，并根據(jk)，(jk)2的系數對應可得：

根據交通流理論，若z2＞0，則交通系統保持穩定狀態，車流平穩行駛；若z2＜0，則交通系統處于不穩定狀態，車流行駛無法保證平穩［30］。

因此通過式（18）可得臨界穩定性曲線方程為：

圖1 為OV 模型、FVD 模型和TD-VDVL 模型的穩定性曲線對比，其優化速度函數都采用式（3）所示的函數，曲線上方為交通系統穩定區域，曲線下方為不穩定區域。通過對圖1的三條曲線進行對比，可以明顯觀測到TD-VDVL 模型比其他兩個模型具有更大的穩定性區域和更小的不穩定性區域。從交通流穩定性的角度上來看，TD-VDVL 模型（λ=0.3，u=0.3，r=0.3）＞FVD 模型（λ=0.3）＞OV 模型。

圖1 臨界穩定性曲線對比Fig.1 Comparison of critical stability curves

圖2（a）是在其他參數確定的情況下（r=0.3，λ=0.3），TD-VDVL 模型中對u的穩定性相位分析圖。由圖2 所示，隨著u的增大，TD-VDVL模型的穩定性區域也在逐步增大，說明在模型中引入時延速度差信息可以有效提高模型的穩定性。

圖2（b）是在u=0.3，λ=0.3 的情況下，對TD-VDVL 模型中的r限速敏感系數進行的穩定性分析。由圖2（b）可以看出，隨著對道路限速信息的敏感度系數的提高，交通系統的穩定性也在提高。

圖2 不同r和u的相位圖Fig.2 Phase diagrams of different r and u

綜上所述，在跟馳模型中引入時延速度差信息和道路限速信息有利于提高交通系統的穩定性。

3 數值仿真實驗與分析

利用Matlab 對TD-VDVL 模型進行數值模擬和仿真分析，研究引入時延速度差和限速信息的跟馳模型對跟馳車流穩定性所起到的綜合作用。

3.1 仿真環境一

在一條長度為L=1 500 m 的仿真直道上［31］，均勻排列著N=100 輛車，設置它們的初始車距為其安全車距即hc=4 m，車道限速為vlim=2 m/s；根據參考文獻［23］設置時延速度差敏感度系數為u=0.3，時延td=1 s；限速敏感系數設置為r=0.3；其他參數都使用經典跟馳模型仿真參數設置，駕駛員敏感系數取值a=0.85，速度差敏感系數λ=0.3，采樣步長為0.1 s；最優速度敏感系數β=1，仿真總步長設置為15 000。

對初始狀態為穩定車流中的第100 輛車施加一個輕微擾動，則此時車流的初始狀態為：

圖3 是t=200 s 和t=600 s 時，OV模型、FVD模型、TD-VDVL 模型中100 輛車的速度分布曲線。從圖3 可以看出，不管是200 s 還是600 s 時，TD-VDVL 模型的車流的速度波動要比OV 模型、FVD 模型中的車流速度波動都要小。隨著時間的推移，可以明顯看到從200～600 s，OV 模型和FVD模型的速度波動越來越大，而TD-VDVL 模型的速度波動越來越小。施加擾動后，擾動在OV 模型和FVD 模型中，沒有隨著時間而消散，反而隨著時間的推移傳播的越來越大，說明FVD 模型和OV 模型不具備消散系統中干擾的能力，容易造成跟馳系統的不穩定，甚至于導致交通堵塞的出現；在TD-VDVL 模型中擾動隨著時間的推移得到控制，說明TD-VDVL 模型具備著較強的消散系統干擾的能力。因此TD-VDVL 模型相較于OV 模型和FVD 模型在消散系統擾動方面具有一定的優越性。

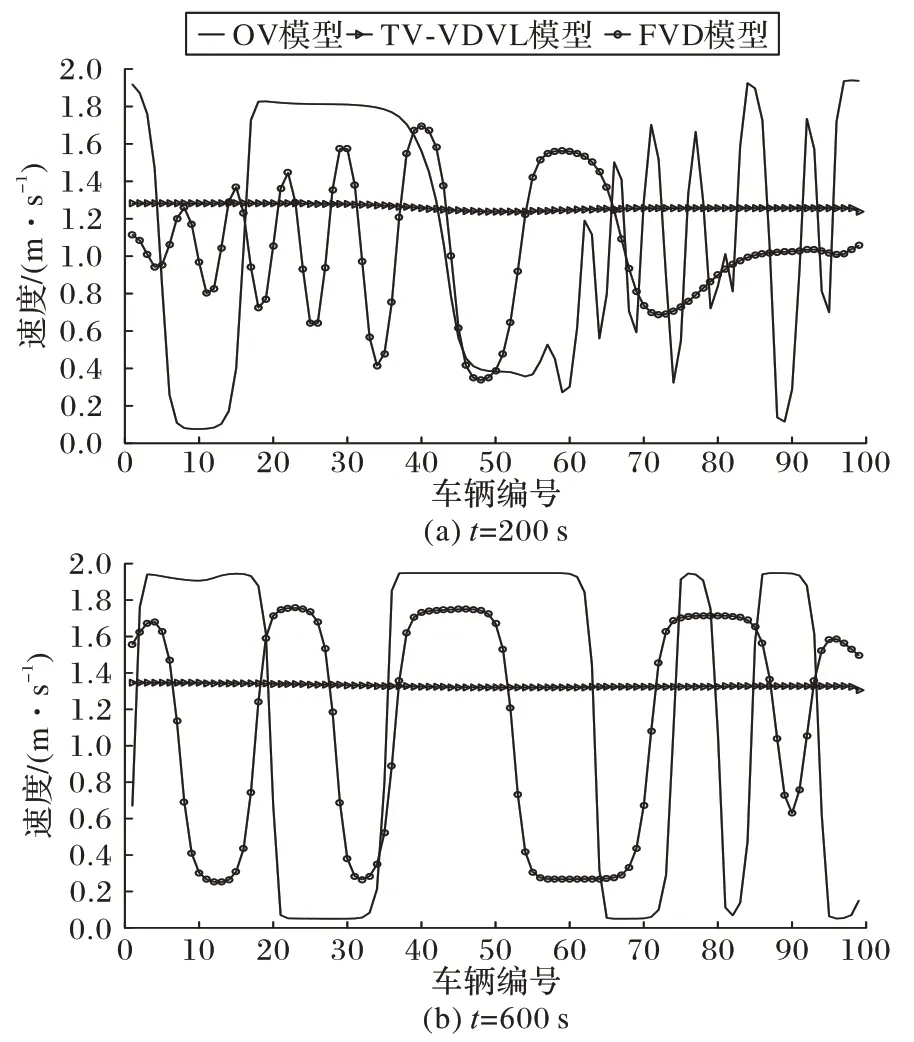
圖3 不同時刻的速度分布Fig.3 Velocity distribution at different time

為了更加直觀地對比3 個模型的穩定性，對t=300 s 和t=500 s 處分別進行了采樣，獲得3 個模型的最小速度、最大速度、平均速度、速度向上波動率、速度向下波動率，以及速度平均波動率，如表1、2 所示。可以清楚發現：OV 模型、FVD模型中跟馳車流的速度波動起伏很大，最大速度和最小速度差特別大，特別是OV 模型的最大速度一直位于在1.9 m/s 左右，而最小速度僅有0.05 m/s。它們的速度波動率也一直處于一個較大的值。其中：OV 模型在500 s 時的速度平均波動率達到78.84%；FVD 模型的速度平均波動率達到67.59%；TD-VDVL 模型的速度波動率一直不大，并且隨著時間的推移，其速度平均波動率還在降低，最大速度和最小速度數值穩定一直保持在1.3 m/s 左右，說明跟馳系統一直處于一個比較穩定的狀態，特別是在500 s 時，速度平均波動率僅有2.35%。實驗結果表明，在相同條件下，TD-VDVL 跟馳模型具備比OV 模型、FVD 模型更優的致穩性，有利于穩定跟馳車流中的車輛速度，降低跟馳車流的速度波動率，從而提高跟馳系統的穩定性；同時也表明，在跟馳模型中引入時延速度差和道路限速信息可以對交通流起到致穩作用。

表1 t=300 s時的速度波動對比表Tab.1 Velocity fluctuation comparison table at 300 s

表2 t=500 s時的速度波動對比表Tab.2 Velocity fluctuation comparison table at 500 s

3.2 仿真環境二

為了更好地研究時延速度差和限速信息對跟馳車流穩定性的影響。參照參考文獻［13］，在一個長度為400 m 的環形道路進行仿真，a設置為0.8，仿真步長為0.01 s，其他參數保持不變。

圖4 是在300 s 和500 s 時TD-VDVL模型在r=0 的情況下，u=0，0.1，0.3 時與r=0.3、u=0.3 情況下100 輛車的車頭間距對比。圖4（c）和（d）是在300 s 和500 s 時TD-VDVL 模型在u=0 的情況下，r=0，0.1，0.3 時與r=0.3、u=0.3 情況下100 輛車的車頭間距對比。通過圖4（a）和（b）的對比以及圖4（c）和（d）對比可以發現，當其他條件保持一致時，改變r或者u的取值，跟馳車流的車頭間距都會發生改變，尤其是當r=0 和u=0 時（即模型退化為FVD 模型時），車頭間距的振動幅度最大，特別是在500 s 時車頭間距波峰波谷差可以達到0.419 6 m，而當r=0.3、u=0.3 時，500 s 的車頭間距的波峰波谷差僅為0.019 4 m。實驗結果表明，FVD 模型在遭受到干擾之后，車頭間距波動很大，并且一直維持在一個較大的數值；改進的TD-VDVL 模型的車頭間距波動不大，因為此時駕駛員考慮了道路的限速信息以及車輛的時延速度差信息，使其可以作出更準確的駕駛決策，從而適應跟馳系統的變化，使跟馳車流中的擾動消散，避免出現交通堵塞的情況。

圖4 不同u和r取值時的車頭間距對比Fig.4 Headway comparison with different r and u

圖5 分別是r和u取不同值時擾動在跟馳車流中傳播時的速度時空變化圖。

圖5 不同r和u取值時的速度時空變化Fig.5 Space-time evolution of velocity with different r and u

從圖5（a）中可以明顯發現：當r=0、u=0 時，此時模型為FVD 模型，在擾動作用下，車流的速度時空圖中出現很多褶皺帶，時空平面出現很多山峰和低谷，說明車流內的速度在不斷變化；并且隨著時間的推移，速度波動越來越大，因為擾動在跟馳車流中不斷傳播并且逐漸被放大，最終影響到交通系統的穩定性，使得整個系統處在不穩定狀態（比如造成交通堵塞），說明FVD 模型對交通系統中干擾的致散性比較差，容易受到外界干擾的影響。在圖5（b）、（c）、（d）中，逐步開始增大r和u的取值，跟馳車流的速度時空圖起伏開始逐漸變小，褶皺帶開始收縮，時空平面的山峰和山谷逐漸變少，在r=0.3、u=0.3 時，褶皺帶已經基本消失，整個速度時空平面基本趨于平緩，說明擾動在跟馳車流中得到控制，甚至消散，交通系統恢復穩定狀態。以上數值仿真實驗以及分析結果表明，在FVD 模型中，引入時延速度差和限速信息，能夠較好地吸收車隊中的擾動，從而進一步提高跟馳車隊的穩定性。

4 結語

在車聯網的環境下，本文提出基于FVD 模型的考慮時延速度差和限速信息的跟馳模型TD-VDVL，通過穩定性分析圖可以看出，TD-VDVL 模型的穩定性區域明顯大于OV 模型和FVD 模型的穩定性區域。數值模擬和仿真實驗結果表明：在實際交通流中，不可以忽視時延速度差和限速信息對跟馳系統的影響，驗證了所提TD-VDVL 模型可以進一步提高跟馳車流的穩定性。這對于開發和完善交通仿真軟件和算法，以及設計相應的駕駛輔助軟件和平臺，輔助駕駛員做出正確的駕駛決策，緩解交通壓力和未來自動駕駛的大規模實施具有一定的指導意義。此外，所提模型并沒有考慮不同車型車輛的時延是否不同，不同道路的限速信息是否不同，這些因素也將影響著跟馳車流的穩定性，在跟馳模型中應該反映這種差異，以便建立更加符合實際情況的跟馳模型，這將是以后的研究和改進方向。