基于自抗擾控制的隨機擾動庫存系統優化模型

趙 川，李璐瑤，楊浩雄，左敏

（北京工商大學電商與物流學院，北京 100048）

0 引言

庫存系統是企業生產運營管理的重要組成部分，也是供應鏈管理領域研究的重要議題［1-4］。近年來自然災害、重大公共衛生等大規模突發事件的頻繁發生，使企業意識到傳統的庫存管理已不足以應對現代突變的市場環境給企業庫存系統帶來的巨大威脅。2020 年6 月，北京新發地批發市場爆發新一輪的新冠病毒聚集性疫情，由于三文魚分割案板呈新冠陽性反應，導致市場對于三文魚的需求銳減，數以噸計的貨物成為燙手山芋；2021 年5 月，受日本福島核污水排放入海決定的影響，韓國大批民眾搶購、囤積海鹽，導致海鹽市場需求激增，多數企業出現庫存不足的現象。在外部需求不確定的環境下，特別是在面對突發事件導致的臨時性撤銷訂單、追加訂單等情況時，如何實現對庫存系統的有效控制，使其保持動態穩定，是眾多企業和學者共同面臨的難題。庫存系統的穩定，在企業運營和供應鏈管理中都具有至關重要的作用。本文旨在對隨機擾動下具有不確定需求的企業庫存系統進行優化，指導企業合理制定訂貨策略，降低庫存波動，弱化市場隨機擾動對企業庫存的影響，從動態系統的角度提高庫存系統的穩定性，為企業的實際生產運營提供科學的理論借鑒和應對方法。

庫存系統控制是通過將企業進銷存中主要動態變量轉換成控制信號、將基本微分方程轉換為狀態控制，合理設計自主反饋控制算法，從而使需求預測量、訂貨量、庫存量等參數達到理想狀態的庫存管理方法［5-8］。現有與本文密切相關的研究主要集中于三方面，即：經典控制理論對庫存的優化、現代控制理論對庫存的優化和自抗擾控制（Active Disturbance Rejection Control，ADRC）算法的應用研究。

Simon［9］首次將控制系統思想應用于庫存控制，將庫存優化問題看作一個控制系統，并用拉普拉斯變換將微分方程轉換成控制系統的傳遞函數。自此，很多學者嘗試從不同角度，使用不同的控制方法研究庫存控制問題，取得了一定成果。Towill 等［10］將生產-庫存分解成3 個子系統：生產延遲時間、庫存調整時間和需求調整時間。文獻［10］在模型中建立了庫存水平與消耗率的關系，證明了反饋控制和前饋控制在庫存管理中的重要性。Jing 等［11］針對閉環供應鏈中的庫存優化和牛鞭效應等問題，通過對單級庫存系統的傳遞函數進行Z 變換后，利用遺傳算法經過參數整定對閉環庫存比例-積分-微分（Proportion-Integral-Derivative，PID）控制后發現，PID 控制器能有效降低庫存和系統的牛鞭效應。此類文獻是本文研究領域的奠基石，也引導了將控制理論與庫存管理相結合的學科交叉；但此類文獻以反饋控制為主，只考慮了系統輸出對輸入的影響，沒有深入分析庫存系統內部的狀態變量。

隨著控制理論的發展，出現了能夠提供系統內部狀態變量的現代控制方法和理論。一些學者將現代控制理論推廣到庫存管理領域，對庫存系統整體進行動態控制。John 等［12］在現代控制理論的基礎上提出了一種基于自動渠道、庫存和定購的生產控制系統模型（Automatic Pipeline，Inventory and Order Based Production Control System，APIOBPCS），企業訂貨量可以根據需求預測量、實際庫存量和理想庫存量等參數來控制。Zhou 等［13］將其擴展到包含生產商、供應商和零售商的三級閉環庫存控制系統，并研究了供應鏈系統的整體動態性、庫存系統的波動性以及牛鞭效應等問題。Zaher 等［14］給出了一個針對庫存問題的隨機微分方程，并將其轉換為最優控制問題，在對問題的描述中，將生產率作為控制變量，庫存量作為狀態變量，構建了庫存系統的狀態方程。Subramanian 等［15］運用分部 式的模型 預測控制（Model Predictive Control，MPC）研究了一個由制造商和零售商組成的二級閉環供應鏈庫存系統。徐君群［16］則從魯棒H∞控制角度研究了具有需求不確定性的動態閉環供應鏈網絡的總成本問題。Zhao 等［17］通過建立庫存系統的狀態空間方程，利用極點配置狀態反饋的方式構建了庫存控制系統，并通過實證研究證明了該系統的可行性與有效性。以上文獻主要從經典的輸出反饋控制、PID 控制以及現代控制理論的角度，分別研究了確定型需求和隨機型需求的庫存系統優化問題。此類文獻以現代控制理論和狀態空間算法為指導，清晰地討論了系統內部狀態變量對庫存的影響；但沒有深入分析系統外部隨機擾動對庫存的影響，也沒有對企業庫存系統如何應對擾動的具體算法進行研究。

自抗擾控制（ADRC）采用直接觀測未知擾動、補償隨機擾動的方式來抑制其對系統產生的影響。一方面，該算法繼承了經典PID 中“利用誤差反饋消除誤差”的優點，使控制系統不依賴于具體模型，僅僅利用誤差進行反饋控制；另一方面，該算法又借助現代控制理論，通過建立擴張狀態觀測器（Extended State Observer，ESO）將系統外部擾動及系統內部動態不確定性合并為總擾動，在其對系統造成嚴重影響之前被估計出來，并通過控制規律和補償機制將其抵消，以此彌補經典PID 的缺陷［18-19］。自抗擾控制以其較好的抗擾動性能和高精度的控制效果，在眾多工程領域都有應用：Gao［20］在自抗擾控制技術推出后，對其進行線性化和參數化整定，簡化了參數調節，便于分析研究，為自抗擾控制技術的工程化和實用化打下基礎；Zhao 等［21］研究了加入具有時變增益的動態函數的非線性自抗擾控制系統，并驗證了其收斂性；Li等［22］設計了一種衛星自抗擾控制算法，用于分析天線系統的動態穩定性，并通過仿真驗證了該模型在實現高指向精度和轉速等方面具有很好的效果；段慧達等［23］針對類似板球系統的一類高階、強耦合、不確定非線性系統，提出以多個低階自抗擾控制器級聯實現控制的方法；Sira-Ramírez 等［24］則將自抗擾控制運用到永磁同步電機的控制上，介紹了一種基于擾動不確定和永久磁鐵同步電動機的角速度軌跡跟蹤任務的自抗擾控制方案，驗證了該方案的魯棒性和有效性。從目前研究現狀來看，自抗擾控制技術非常適用于系統的抗擾研究，尤其是在無法對突發隨機擾動進行數學描述的情況下，可以強有力地補償擾動對系統造成的影響，維持系統的動態穩定；但自抗擾控制主要應用于工程控制領域，在企業庫存管理及庫存控制方面還未見涉及。

本文在上述研究的基礎上，針對企業庫存運營管理的內在邏輯和隨機市場需求特點，將臨時性追加和撤銷訂單視為隨機擾動。結合自抗擾算法的控制機理和適用條件，削弱短時隨機擾動對庫存系統的影響，進一步對企業庫存系統的控制優化問題展開研究。

本文的主要工作如下：

1）建立了庫存系統的二階狀態空間模型，在隨機需求基礎上增加了代表臨時追加和撤銷訂單的隨機擾動。

2）設計了一種基于具有跟蹤微分器安排需求信號過渡、擴張狀態觀測器對隨機擾動擴張觀測和非線性狀態反饋律進行控制補償作用的自抗擾控制隨機擾動庫存系統優化模型。

3）通過對基于自抗擾控制的隨機擾動庫存系統優化模型進行參數整定和優化，進一步提高了系統的控制效果和控制精度。

1 隨機擾動下庫存系統狀態空間建模

在一個常見的生產或分銷企業中，與進銷存過程密切相關的基本變量有：企業向上游發送訂單的訂貨量、企業內部形成的庫存量和企業收到下游的訂單，即實際需求量。以上3 個變量相互影響，最終決定企業的庫存水平和庫存成本。本文采用“定至點”訂貨策略，具體而言，在一個訂貨周期內，企業首先向供應鏈上級供應商進行訂貨，到貨后形成本周期庫存，并根據市場需求銷售貨物；其次，到本周期期末，企業一方面對現有庫存量即銷售后的剩余庫存量進行盤點，另一方面，根據本周期的實際銷售情況，對下一周期市場需求進行預測；最后，企業根據本周期現有庫存量與下一周期預測需求量的偏差，制定具體的訂貨策略。為方便本文建立企業庫存系統的動態數學模型，本文參數設置如表1 所示。

表1 參數設置Tab.1 Setting of parameters

本文假設：I(t)和Df(t)為系統的狀態變量；D(t)為系統的輸入；O(t)為系統的輸出，即：訂貨量通過現有庫存量和預測需求量對訂貨量產生影響。其次假設研究期間內企業訂貨周期不變，配送期間不存在貨損和延遲送貨等情況。

根據企業庫存管理基本邏輯，t+1 時的期初庫存量等于t時的期初庫存量加上t時段內企業向上游的訂貨量，減去t時段內實際需求量，即：

根據泰勒展開式，對于庫存函數有：

其中：n！表示階乘，Rn(t)表示泰勒展開式和實際值之間的余數，由此可以得到庫存函數的一階導數的近似值：

假設R1(t)足夠小，求解得到t時的邊際庫存量為：

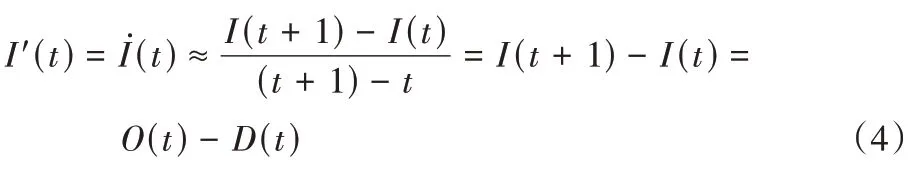
t時段內的訂貨量為t時段的需求預測量減去t時段的現有庫存量：

代入式（4）得：

根據指數平滑法預測模型，得到t時期內平滑指數為α的需求預測模型：

同樣由泰勒展開得到邊際需求預測量：

變換式（4）得：

根據狀態空間描述式：

結合企業庫存系統的數學模型（6）～（9），得到無隨機擾動時的企業庫存系統狀態空間基本描述式：

為建立含有隨機擾動的庫存系統狀態空間，需將庫存狀態空間轉化成復頻域傳遞函數后再加入動態隨機擾動。首先，由將企業庫存系統的狀態空間轉換為傳遞函數后得：

其中：E為單位矩陣，S為復頻域算子，進一步可得該狀態方程的等效傳遞函數為：

最終得到考慮隨機擾動的庫存狀態空間標準式：

將此標準式轉化為適用于抗擾控制算法的多級串聯標準型［25-26］：

為得到f1、f2及b，需令y=x1，將輸出y(t)的輸入輸出關系轉化為狀態變量的控制關系。由式（17）可知=x2，得到f1=0。

對輸出y(t)求導，可得：

由式（17）可知存在如下關系：

將式（21）代入式（20）可得：

綜上所述，式（17）庫存狀態空間標準式可轉化為一類標準的二階狀態空間系統：

2 基于自抗擾控制的隨機擾動庫存系統優化模型設計

自抗擾控制算法能對系統外部干擾起到較好的抑制和弱化作用，尤其適用于不確定性因素影響下的動態系統。本文針對企業在訂單激增，臨時撤單等情況下，庫存系統受外部隨機干擾較嚴重時無法快速、穩定地恢復原有狀態的問題，設計了一種基于自抗擾控制的隨機擾動庫存系統優化模型。該基于自抗擾控制的隨機擾動庫存系統優化模型主要由跟蹤微分器（Tracking Differentiator，TD）、擴張狀態觀測器和非線性狀態誤差反饋控制律（Nonlinear State Error Feedback Control Law，NLSEF）三部分相互作用形成［27］，其內部結構如圖2 所示。

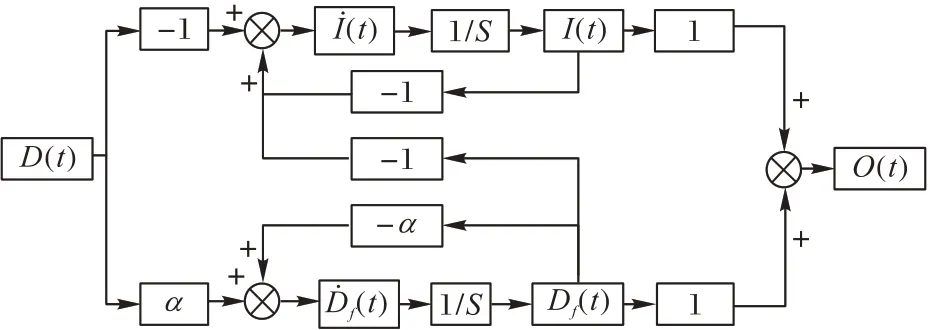
圖1 企業庫存系統狀態空間框圖Fig.1 Block diagram of enterprise inventory system

圖2 基于自抗擾控制的隨機擾動庫存系統優化模型框圖Fig.2 Block diagram of optimization model of inventory system under stochastic disturbance based on ADRC

自抗擾控制通過對企業庫存系統受到的隨機擾動進行估計，主動補償擾動對庫存系統的影響，從而實現隨機擾動下企業庫存系統的控制和優化。具體來說，跟蹤微分器能夠提取系統輸入市場需求中的擾動信號，對信號進行跟蹤和輸入，進而控制隨機擾動下庫存系統的最大響應幅度和響應時間；擴張狀態觀測器通過對隨機擾動信號進行狀態估計，形成合理的控制信號，削弱隨機擾動對庫存系統的影響；非線性狀態誤差反饋控制律根據庫存系統受到擾動時和正常情況下的庫存狀態差值，確定相應的控制量，配合擴張狀態觀測器對庫存系統進行及時調整。

首先設計跟蹤微分器。為使庫存系統的外部市場需求信號更易跟蹤，降低外部隨機擾動的干擾，弱化反饋誤差，本文對目標需求信號，即實際市場需求，采用一種過渡過程進行處理。定義如下跟蹤微分方程組，其二階形式為：

其中控制量u采用如下形式：

采用v(k)為輸入的目標需求信號，v1(k)為目標需求信號v(k)的跟蹤信號，v2(k)為v1(k)的微分信號，r為速度因子，h為非線性函數fhan(·)的采樣時間，其跟蹤微分表達式參照文獻［27］設計為組合式（28）的形式：

通過跟蹤微分算法可將較為柔和的跟蹤信號v1(k)代替被擾動的目標需求信號v(k)，并得到較為光滑的微分信號v2(k)，進而更好地實現后面的控制優化模型。

其次，設計擴張狀態觀測器。對于庫存系統外部的市場隨機擾動，本文通過構造擴張狀態觀測方程組對其進行觀測，并進行補償。在式（24）中，將系統內部擾動和外部擾動納入f(x1，x2，t)中，對于式（25）所示的二階系統，本文定義如下形式的擴張狀態觀測方程組：

其中：y(t)為系統輸出，zi(t)(i=1，2，3)為觀測值，e(t)為ESO觀測誤差，β0i為觀測器增益系數，fal(e，λ，δ)為非線性函數，其算法［27］為：

其中，δ是為了防止誤差接近于零時增益過大而產生庫存系統較大波動而設置的線性區間長度，區間為(-δ，δ)。

最后，設計非線性狀態誤差反饋控制律。在線性反饋下，系統的穩態誤差與反饋增益成反比，而在非線性反饋下系統的穩態誤差與使用的非線性函數有關，故自抗擾控制通過選用適合的非線性函數來生成控制量。本文中采用如下形式的非線性反饋函數：

其中：z3為擴張狀態觀測器中針對擾動部分被擴張出來的觀測狀態，b為補償因子，u為補償庫存系統和擾動作用的分量。非線性反饋控制律可以使庫存系統通過補償隨機擾動從而生成預測需求量來指導企業庫存系統進行合理訂貨（即系統輸出）。

至此，基于自抗擾控制的隨機擾動庫存系統優化模型已設計完畢，其Simulink 框圖如圖3 所示。

圖3 基于自抗擾控制的隨機擾動庫存系統優化模型仿真框圖Fig.3 Simulation block diagram of optimization model of inventory system under stochastic disturbance based on ADRC

3 仿真與對比研究

為驗證基于自抗擾控制的隨機擾動庫存系統優化模型的有效性，本文應用Matlab/Simulink 平臺對自抗擾控制器進行設計，并對企業隨機擾動庫存系統進行仿真優化研究。具體實驗步驟為：首先，搭建基于自抗擾控制的隨機擾動庫存系統優化模型，包括跟蹤微分器、擴張狀態觀測器、非線性狀態誤差反饋控制律和企業動態庫存系統；其次，對基于自抗擾控制的隨機擾動庫存系統優化模型進行參數整定與優化，選取與動態庫存系統相匹配的參數組合，以提高系統的控制效果和控制精度；最后，以庫存系統的缺貨次數、剩余庫存均值、剩余庫存標準差、進貨量均值和進貨量標準差為控制指標，對仿真結果進行綜合分析，驗證基于自抗擾控制的隨機擾動庫存系統優化模型的優化效果。

3.1 參數整定與優化

本文在Simulink 平臺中對優化模型進行仿真，采用階躍信號和波動相對平穩的正弦信號進行參數整定測試，由于平滑指數取值取決于數據源的波動程度，即波動較大時，α相對較大，波動平穩時，α取值較小，0 ＜α＜1［28］。針對采用階躍信號的參數實驗階段，取平滑指數α=0.8。

對于基于自抗擾控制的隨機擾動庫存系統優化模型而言，參數整定是首要問題。在本文設計的基于自抗擾控制的隨機擾動庫存系統優化模型中，跟蹤微分環節的參數r、h的調整能夠有效解決系統超調問題，即當市場需求受擾動干擾發生巨大變化時，期望庫存的超調量不會過大。擴張狀態觀測環節中，參數β01、β02及β03的具體選擇由系統的采樣步長決定，它們主要解決系統滯后性和振蕩問題，在具體的調節過程中可先調節β03觀測效果，直到系統跟蹤效果較好時，再對β01、β02進行調節以提升控制系統性能，使需求預測能快速低滯后、穩定無振蕩地跟隨市場實際需求的變化而變化。非線性反饋控制律中，k1、k2為非線性函數fal(·)前的系數，b為補償因子，主要用于補償外部擾動，以使期望庫存的設定能在抗干擾環境下跟隨市場需求波動［29-30］。

首先對基于自抗擾控制的隨機擾動庫存系統優化模型進行參數整定，自抗擾控制各環節初始狀態下各參數為：

跟蹤微分環節r=120，h=0.8。

狀態觀測環節β01=80，β02=55，β03=70。

非線性反饋率k1=25，k2=30。

初始狀態下，優化模型跟蹤曲線如圖4 所示，由圖4 可見，系統響應振蕩較多、幅度較大且響應速度較慢。

圖4 基于自抗擾控制的隨機擾動庫存系統優化模型初始狀態下跟蹤曲線Fig.4 Tracking curve of optimization model of inventory system under stochastic disturbance based on ADRC in initial state

初始狀態下，基于自抗擾控制的隨機擾動庫存系統優化模型的階躍響應如圖5 所示。

圖5 基于自抗擾控制的隨機擾動庫存系統優化模型初始狀態下階躍響應Fig.5 Step response of optimization model of inventory system under stochastic disturbance based on ADRC in initial state

通過實驗可以看出，在階躍響應中，初始狀態的基于自抗擾控制的隨機擾動庫存系統優化模型的超調量達到60%，調節時間為70 s。

為使庫存系統對隨機擾動下需求的響應達到準確、快速、穩定、超調小的目的，對系統各環節不同參數進行整定，經過大量實驗后最后確定最優參數組合，結果如下：

跟蹤微分環節r=150，h=1。

狀態觀測環節β01=10，β02=100，β03=10。

非線性反饋率k1=95，k2=20。

參數整定后，對應的跟蹤曲線如圖6 所示。與圖4 相比，在系統的上升與下降沿部分，響應速度均有相對提高，響應振蕩幅度明顯減小，自抗擾控制器跟蹤精度有較大的提高。

圖6 基于自抗擾控制的隨機擾動庫存系統優化模型參數整定后跟蹤曲線Fig.6 Tracking curve of optimization model of inventory system under stochastic disturbance based on ADRC after parameter tuning

參數整定后，基于自抗擾控制的隨機擾動庫存系統優化模型的階躍響應結果如圖7 所示。

圖7 基于自抗擾控制的隨機擾動庫存系統優化模型參數整定后階躍響應Fig.7 Step response of optimization model of inventory system under stochastic disturbance based on ADRC after parameter tuning

通過實驗結果可以看出，參數整定后的階躍實驗中，優化模型的超調量由60%下降到50%，達到穩定狀態的調節時間也下降為40 s，系統的控制效果較好。因此，通過對優化模型的跟蹤精度、超調量和調節時間進行觀測，可知該組參數組合適用于本文所提出的基于自抗擾控制的隨機擾動庫存系統優化模型。

3.2 仿真對比

在基于自抗擾控制的隨機擾動庫存系統優化模型中，企業每一周期對需求的預測要根據歷史實際需求信息制定，而實際需求除正常波動外還會受諸多不確定擾動影響，如臨時加單、撤單，這增強了其不確定性，加大了庫存系統的控制難度。當需求波動伴隨隨機擾動信號輸入基于自抗擾控制的隨機擾動庫存系統優化模型時，自抗擾控制器會對其進行觀測并模擬，通過狀態反饋控制輸出，指導企業訂貨決策，保證庫存系統在隨機擾動下仍能穩定運行，降低庫存成本。本文收集了某大型批發市場自2018 年1 月至2019 年12 月中50個周期米醋的實際銷售量進行實證研究，如表2 所示，其平均值為347，標準差為202；除此之外，在第15、30、35 周期增加持續時間為1 s 的3 個振幅分別為500、500 和-400 的不定時正負脈沖信號作為隨機擾動量，即在實際市場需求的基礎上增加瞬時擾動，采用上述參數整定優化后的基于自抗擾控制的隨機擾動庫存系統優化模型進行仿真對比。

表2 某批發市場米醋實際銷售量數據Tab.2 Actual sales volume data of rice vinegar in wholesale market

為驗證基于自抗擾控制的隨機擾動庫存系統優化模型的有效性，本文對庫存系統進行三個仿真實驗，分別為：無隨機擾動庫存系統仿真、隨機擾動庫存系統仿真和基于自抗擾控制的隨機擾動庫存系統優化模型仿真。

三種庫存系統的訂貨量仿真結果如表3 所示。

表3 庫存系統訂貨量仿真結果Tab.3 Simulation results of order quantity in inventory system

三種庫存系統的訂貨量仿真對比如圖8 所示。結果表明，在隨機擾動的影響下，企業訂貨量波動明顯增大；而基于自抗擾控制的隨機擾動庫存系統優化模型能夠弱化隨機擾動對企業庫存系統的影響，保證其穩定運行，指導企業進行合理訂貨。

圖8 庫存系統訂貨量對比Fig.8 Comparison of order quantity in inventory system

圖9 為庫存系統訂貨量移動標準差對比情況。基于自抗擾控制的隨機擾動庫存系統優化模型訂貨量移動標準差略小于無隨機擾動庫存系統，明顯小于隨機擾動庫存系統。結果表明，自抗擾控制系統不僅能夠削弱隨機擾動對企業訂貨決策的影響，還能夠進一步修正市場實際需求，使庫存系統對需求響應能夠達到抗擾、準確、快速、穩定的效果，降低企業訂貨波動。

圖9 庫存系統訂貨量移動標準差對比Fig.9 Comparison of order quantity moving standard deviation in inventory system

圖10 為庫存系統訂貨量移動均值對比情況，無隨機擾動企業訂貨量均值為349；隨機擾動企業訂貨量均值為364；而基于自抗擾控制的隨機擾動庫存系統優化模型的企業訂貨量均值為358。實驗結果證明，基于自抗擾控制的隨機擾動庫存系統優化模型能夠有效減小企業訂貨量，合理利用資源，降低庫存成本。

圖10 庫存系統訂貨量移動均值對比Fig.10 Comparison of order quantity moving mean in inventory system

三種庫存系統的剩余庫存量仿真結果如表4 所示。

表4 庫存系統剩余庫存量仿真結果Tab.4 Simulation results of residual inventory in inventory system

三種庫存系統的剩余庫存量仿真對比如圖11 所示，隨機擾動擾亂企業庫存系統，分別在第16 和第32 周期出現2次缺貨現象；而自抗擾控制能夠優化庫存系統，穩定企業庫存，完全改善缺貨現象。

圖11 庫存系統剩余庫存量對比Fig.11 Comparison of residual inventory in inventory system

圖12 為庫存系統剩余庫存量移動標準差的對比情況。由圖可知，自抗擾控制能夠弱化隨機擾動對企業庫存系統的影響，減小庫存波動，使其處于相對穩定運行的狀態。

圖12 庫存系統剩余庫存量移動標準差對比Fig.12 Comparison of residual inventory moving standard deviation in inventory system

圖13 為庫存系統剩余庫存量移動均值的對比情況，無隨機擾動企業平均剩余庫存量為145，隨機擾動企業平均剩余庫存量為320，而基于自抗擾控制的隨機擾動庫存系統優化模型的企業平均剩余庫存為237。結果表明，基于自抗擾控制的隨機擾動庫存系統優化模型能夠有效改善由外部隨機擾動引起的庫存大量積壓現象，減少資源浪費。

圖13 庫存系統剩余庫存量移動均值對比Fig.13 Comparison of residual inventory moving mean in inventory system

為了更加直觀地體現基于自抗擾控制的隨機擾動庫存系統優化模型的優化效果，現將無隨機擾動、隨機擾動和基于自抗擾控制的隨機擾動庫存系統優化模型仿真結果量化形成對比表，如表5 所示。

表5 三種模型仿真結果對比Tab.5 Comparison of simulation results of three models

4 結語

本文針對隨機擾動企業庫存控制問題進行深入研究，從工程控制的角度，建立了基于動態微分方程的庫存系統狀態空間模型，并通過拉普拉斯變換對庫存系統的傳遞函數進行推導，進而得到自抗擾控制受控對象的標準形式，建立基于自抗擾控制的隨機擾動庫存系統優化模型。為提高基于自抗擾控制的隨機擾動庫存系統優化模型的精準程度并驗證其控制效果，本文通過大量實驗對基于自抗擾控制的隨機擾動庫存系統優化模型進行復雜參數整定與優化，確定一組最優控制參數組合；收集某大型批發市場實際銷售量數據作為系統輸入，并使用Simulink 軟件對系統進行仿真實驗。仿真實驗表明，隨機擾動使企業無法快速、準確地識別真實市場需求并及時調整訂貨策略，進而導致缺貨、庫存積壓和庫存成本過高的現象。基于自抗擾控制的隨機擾動庫存系統優化模型能夠修正庫存系統輸入，指導企業科學、合理地制定訂貨策略，進而保證庫存系統穩定運行。在消除缺貨現象的基礎上，降低庫存持有量，減小庫存積壓，有效弱化市場隨機擾動對企業庫存系統的影響。

本文應用自抗擾控制實現隨機擾動下的庫存系統動態優化，從而為企業庫存系統抗擾和穩定運營提供優化策略，降低不穩定性輸入導致的運營成本，為企業的實際生產運營提供理論借鑒和應對方法。依托本文隨機擾動下庫存自抗擾優化模型，可以進一步進行相關拓展研究。本文為方便計算，使用指數平滑預測法進行需求預測，未來可采用神經網絡等算法進行更精準的需求預測；除此之外，本文只考慮了單級庫存系統，未來可針對供應鏈多級庫存系統進行研究。