MATLAB在“大學(xué)物理”課程學(xué)習(xí)中的應(yīng)用

黃旭初，李艷青

（昌吉學(xué)院 物理系，新疆 昌吉 831100）

“大學(xué)物理”是理科、工科、農(nóng)學(xué)和醫(yī)學(xué)專業(yè)的基礎(chǔ)課程，其內(nèi)容覆蓋范圍廣、知識較為抽象，并且在學(xué)習(xí)過程中需要一定的數(shù)學(xué)知識，這給廣大學(xué)生的學(xué)習(xí)帶來了一定的困難。對于一般的本科院校來說，“大學(xué)物理”這門課通常是開設(shè)在大學(xué)的第一學(xué)年，基本上與高等數(shù)學(xué)同步開設(shè)，然而在這個階段，大多數(shù)學(xué)生利用積分、求導(dǎo)、極限等數(shù)學(xué)工具解決物理問題的能力略顯不足。由于數(shù)學(xué)知識的薄弱，導(dǎo)致學(xué)生無法很好地理解物理問題，這極大地削弱了學(xué)生對物理的學(xué)習(xí)興趣。針對這個問題，通過課程改革取得了一定的成效，例如，用混合教學(xué)將線上和線下相互結(jié)合，調(diào)整教學(xué)內(nèi)容和教學(xué)方法等。然而，大學(xué)物理知識具有較強的邏輯關(guān)聯(lián)性，知識結(jié)構(gòu)環(huán)環(huán)相扣，同時這門課是訓(xùn)練學(xué)生思維方式的一個過程，因此，從形式上或者結(jié)構(gòu)順序上的調(diào)整仍無法從根本上解決這個問題。為此，我們提出利用一些科學(xué)軟件來輔助學(xué)習(xí)，這不僅能夠克服數(shù)學(xué)上的障礙，同時還能將抽象的物理問題形象化，進而抓住物理的本質(zhì)，加深對物理問題的理解，從而能夠有效地提高學(xué)習(xí)效率，激發(fā)學(xué)生的學(xué)習(xí)興趣。

目前，常見科學(xué)軟件有Mathematic、MATLAB、Excel等，其中MATLAB以簡單易學(xué)、函數(shù)豐富、數(shù)形結(jié)合便捷等優(yōu)勢被廣大師生所青睞。由于MATLAB包含較為完善的數(shù)學(xué)函數(shù)，編程語言通俗易懂，學(xué)生容易掌握，因此利用MATLAB輔助學(xué)習(xí)大學(xué)物理成為可行。如何利用MATLAB處理大學(xué)物理中的物理問題，將物理問題圖形化是提高學(xué)習(xí)興趣的關(guān)鍵，本文就圍繞這個問題選取力學(xué)、電磁學(xué)和機械波的相關(guān)知識點展開論述。

一、“大學(xué)物理”中的數(shù)學(xué)問題

在大學(xué)物理的知識結(jié)構(gòu)中，質(zhì)點的運動及其運動規(guī)律是最為簡單、最基礎(chǔ)的章節(jié)，在這個章節(jié)中部分學(xué)生對位移、速度和加速度這三者之間相互關(guān)系的理解停留在高中的階段，也就是會用一些現(xiàn)有的公式來處理質(zhì)點的運動問題。用以前學(xué)過的知識處理質(zhì)點運動問題，這說明學(xué)生對相關(guān)數(shù)學(xué)知識的理解和應(yīng)用欠缺，導(dǎo)致的結(jié)果就是思維方式?jīng)]有發(fā)生轉(zhuǎn)變，在后續(xù)的學(xué)習(xí)過程中就變得非常吃力，從而覺得大學(xué)物理很難，逐漸失去對大學(xué)物理的學(xué)習(xí)興趣。在質(zhì)點的運動章節(jié)中應(yīng)用的數(shù)學(xué)知識主要是求導(dǎo)、積分和極限，如果能夠把這些知識點的物理和數(shù)學(xué)之間的關(guān)系理解清楚，就能在后續(xù)的學(xué)習(xí)過程中得心應(yīng)手。

對于極限在質(zhì)點運動中的應(yīng)用主要是體現(xiàn)在平均和瞬時之間的關(guān)系上，如瞬時速度是將平均速度的時間取極限，從物理角度來理解就是時間點和時間段的變化。用MATLAB來取一個函數(shù)的極限可以用limit（r,t,0）的形式直接調(diào)用，其中r表示位置矢量函數(shù)，t是時間參量，0表示讓時間變量t無限趨近于零。例如已知運動一質(zhì)點沿著x軸運動的位置和時間的關(guān)系由方程x=50t+5t確定，求質(zhì)點在最初3秒內(nèi)的平均速度和質(zhì)點在t=3s時的瞬時速度？對于這樣的問題，平均速度可以按照定義在MATLAB中輸入v=（50*3+5*3^2-0）/（3-0）直接計算，瞬時速度就可以用v=limit（（50*t+5*t^2-50*3-5*3^2）/（t-3）,t,3）計算。如果按照數(shù)學(xué)中導(dǎo)數(shù)的定義，將平均速度中時間的變化量取極限就是位移對時間的導(dǎo)數(shù)，即=/就是瞬時速度，那么這個問題在MATLAB中就可以更為簡便的直接調(diào)用導(dǎo)數(shù)函數(shù)v=diff（50*t+5*t^2,1），在獲得任意時刻的瞬時速度v=50+10*t基礎(chǔ)上，代入t=3s求得答案。

在“大學(xué)物理”課程中對于導(dǎo)數(shù)的應(yīng)用，主要體現(xiàn)在考察兩個變量之間的對應(yīng)關(guān)系上，例如位移隨時間的變化、動量隨時間的變化和熱量隨溫度的變化等。對于這個知識點的學(xué)習(xí)，學(xué)生遇到的問題主要有兩點：第一，對于導(dǎo)數(shù)的基本公式?jīng)]有很好的掌握，在應(yīng)用的時候拿不準(zhǔn)，需要查閱記分表，特別是在復(fù)合求導(dǎo)和偏導(dǎo)數(shù)計算中容易出錯；第二，由于在高等數(shù)學(xué)中導(dǎo)數(shù)的定義是建立在標(biāo)量基礎(chǔ)上，對于矢量的求導(dǎo)學(xué)生不太容易理解。在“大學(xué)物理”教學(xué)過程中，為了能夠讓學(xué)生更好地理解矢量的求導(dǎo)，通常是將導(dǎo)數(shù)用極限的形式表示出來，考慮變化矢量的大小和方向在取極限條件下隨另一個物理量之間的變換關(guān)系。如在質(zhì)點的圓周運動中，切向單位矢量對時間的導(dǎo)數(shù)d/dt，可以寫成lim（|Δ|）n/Δt=（/R）n，學(xué)生很難理解為什么切線方向的單位矢量求導(dǎo)會轉(zhuǎn)到法線方向。MATLAB軟件的基礎(chǔ)是函數(shù)的矩陣表示，矢量用矩陣形式計算是非常便捷的，從而我們可以用MATLAB對這個問題做一個簡單的說明。假設(shè)切線方向初始單位矢量A=［cosθ,sinθ］，末態(tài)單位矢量為B=［cos（θ+Δθ）,sin（θ+Δθ）］，則單位矢量的變化量C=B-A=［cos（θ+Δθ）-cosθ,sin（θ+Δθ）-sinθ］。要確定兩個矢量相互垂直，只需要證明它們的點乘為零，用MATLAB可以調(diào)用limit（dot（C,B）,Δθ,0）或 者limit（dot（C,A）,Δθ,0）來得到這個結(jié)果。這樣處理一方面加深了對極限和導(dǎo)數(shù)的理解，另一方面簡化了矢量的運算，從而讓學(xué)生不再為數(shù)學(xué)問題所困擾，而更加關(guān)注對物理問題的理解。

積分在大學(xué)物理中的應(yīng)用非常廣泛，但是學(xué)生在學(xué)習(xí)過程中卻比較吃力，主要是因為學(xué)生記不住積分公式，或者對于積分的上下限模糊不清。由于積分是相對于導(dǎo)數(shù)的逆變換，所以在大學(xué)物理中只要有求導(dǎo)通常都會出現(xiàn)積分，并且積分變換后擁有相應(yīng)的物理含義，例如牛頓第二定律F=dP/dt，這個式子原本表示的是動量隨時間的變換關(guān)系，經(jīng)過積分變換后ΔP= Fdt就表示質(zhì)點的動量定理。在大學(xué)物理中積分可以理解為取極限情況下對某一個物理量的求和，而積分上下限對應(yīng)的是邊界條件，結(jié)合MATLAB就很容易克服積分帶來的困擾。在質(zhì)點運動章節(jié)中，例如已知質(zhì)點沿x軸直線運動，加速度為=4-（/），初始條件=3時，=2/，求質(zhì)點的速度。由加速度的定義可以得到=（4-），對這個式子兩邊同時積分就能得到速度的表達式=+4-/3，參量是通過帶入初始條件求得。應(yīng)用MATLAB可以調(diào)用int（1,v,v0,v）和int（4-t,t,0,t）對兩邊進行積分，獲得任意時刻速度的表達式。當(dāng)然，這樣簡單的函數(shù)應(yīng)用MATLAB似乎沒有太多的簡化，然而面對一些復(fù)雜的函數(shù)時，MATLAB的優(yōu)勢就會顯現(xiàn)出來。學(xué)生在學(xué)習(xí)過程中，從質(zhì)點的運動開始能夠逐漸用MATLAB輔助學(xué)習(xí)，能夠很好地起到過渡作用，隨著數(shù)學(xué)和物理知識的逐步深化，處理復(fù)雜問題的能力也會逐步增強。例如在熱學(xué)部分和電磁學(xué)部分不僅會用到極限、導(dǎo)數(shù)和積分這樣一些知識，還會用到級數(shù)展開，特殊函數(shù)及微分方程的求解等知識，同樣這些問題也能結(jié)合MATLAB進行處理。

二、物理問題的圖形處理

在學(xué)習(xí)過程中，通常圖形與復(fù)雜的數(shù)學(xué)公式相比更為直觀、具體，對于物理問題的理解也更容易一些。MATLAB不僅能夠?qū)σ恍┖瘮?shù)直接調(diào)用，同時還能夠?qū)⑦@些函數(shù)用圖的形式展示出來，綜合了計算和畫圖功能，這使得能夠更為直觀的分析物理問題。下面我們通過兩個較為抽象的物理問題為例，探討如何應(yīng)用MATLAB將抽象的概念圖形化，分析相應(yīng)的物理本質(zhì)。電磁學(xué)章節(jié)中電場和電勢的分布，僅通過點電荷的電場強度和電勢公式很難看出它們的分布情況，對于電場強度和電勢之間的關(guān)系也不容易掌握。然而，將點電荷電勢的公式直接輸入到MATLAB中，并且調(diào)用梯度函數(shù)gradient，等值線函數(shù)contour和矢量函數(shù)quiver就能將電勢和電場強度之間的關(guān)系很好的展示出來，如圖1所示。

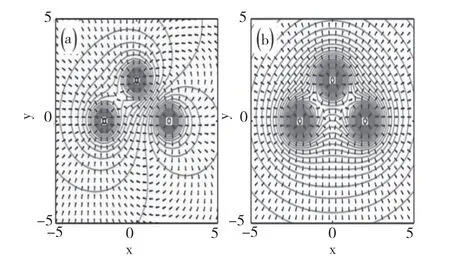
圖1 等電量的三個點電荷周圍電場線和電勢分布圖，（a）和（b）分別表示三個異號電荷和同號電荷的電場線和電勢分布情況

在做“大學(xué)物理”實驗中，描繪多個點電荷的電場線讓多數(shù)同學(xué)都感到很困難，通過這樣一個輔助計算就可以將理論和實驗緊密結(jié)合起來，從而更加主動地思考更深層次的一些物理問題。從圖1中我們可以看到在x-y平面中，空間各點的電場強度我們都可以用一個具有一定長度的箭頭來表示。從箭頭的方向可以反映出電場強度在空間各點方向的變化。基于電場強度和電勢的關(guān)系，可以從等勢線的疏密程度看出電場強度的大小。由于模擬過程中是按照相等的電勢差為單位間隔，從而我們可以看到靠近電極位置等勢線密集反映出較大的電場強度，較遠的地方稀疏反映出較小的電場強度。

在機械波的學(xué)習(xí)中，波的疊加和干涉都是通過數(shù)學(xué)計算，然后對相應(yīng)的物理量進行分析，從而研究波的性質(zhì)。對于波的性質(zhì)研究，用MATLAB畫圖是比較方便的，例如用mesh對相干波進行畫圖，能夠很直觀地看到空間各質(zhì)點的振動情況，振動加強和振動減弱點的位置及它們與波源、頻率、波長等參量的關(guān)系都能清晰地展現(xiàn)，如圖2所示。

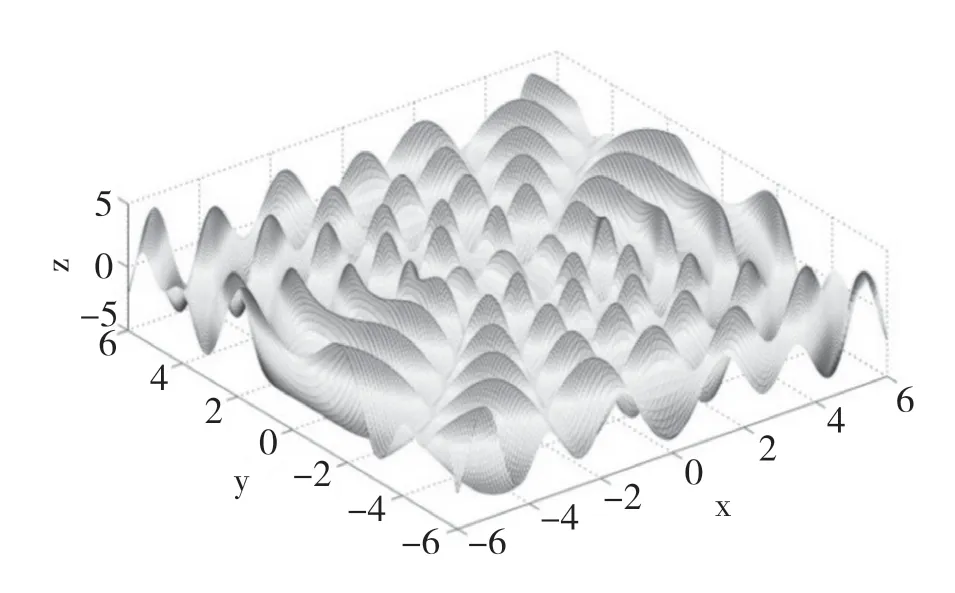
圖2 波源分別位于x-y平面（2，0）和（-2，0）兩點的兩相干波的干涉圖樣

在用MATLAB對相干波進行表示的過程中，不需要復(fù)雜的計算，學(xué)生可以通過修改波長、頻率或者傳播方向等參量來研究不同情況下波的圖樣。這里我們是選取了波源位于x-y平面（2，0）和（-2，0）的兩點。從圖上我們可以看到，在z方向振幅出現(xiàn)了明顯的加強和減弱現(xiàn)象，而且這種振幅的變化呈現(xiàn)一種對稱分布。通過調(diào)整參數(shù)如改變波源的位置，或者用球面波或者柱面波就會使得干涉圖樣呈現(xiàn)出其他的變化形態(tài)。在“大學(xué)物理”中用MATLAB把物理問題圖形處理的優(yōu)勢就省去了復(fù)雜的計算，可以直觀的研究物理問題，并且把物理問題進一步的深化。例如機械波的問題可以適當(dāng)?shù)財U展到電磁場的傳播，或者是光學(xué)的關(guān)涉等問題。這種用MATLAB圖形研究物理問題，隨著大學(xué)物理知識由淺入深的學(xué)習(xí)，對于培養(yǎng)相關(guān)專業(yè)學(xué)生的思維能力和創(chuàng)新能力有很大的提升，同時，克服了物理問題抽象化給學(xué)生帶來的困擾。

三、應(yīng)注意的一些問題

應(yīng)用MATLAB輔助大學(xué)物理的學(xué)習(xí)具有很多優(yōu)勢，然而，在分析具體的物理問題時要考慮到軟件的局限性，分清編程語言和物理問題之間的聯(lián)系和區(qū)別。在應(yīng)用MATLAB處理物理問題過程中，要注意三方面的問題：第一，要明確物理問題和MATLAB語言之間的對應(yīng)關(guān)系。很多學(xué)生在應(yīng)用MATLAB語言表達物理問題的時候不夠準(zhǔn)確，往往會導(dǎo)致結(jié)果不準(zhǔn)，甚至是錯誤的結(jié)論。因此，將一個抽象的物理問題具體用MATLAB語言描述的時候就必須抓住問題的本質(zhì)，前后推敲仔細驗證。第二，處理物理問題過程中要考慮到MATLAB的局限性。通常在物理學(xué)中能夠測量的物理量都是實數(shù)，然而應(yīng)用MATLAB進行數(shù)學(xué)計算的時候會出現(xiàn)復(fù)數(shù)的情況，這就需要在物理問題的描述過程中加一些限制條件。另一方面用MATLAB表示物理問題的時候是用點（或數(shù)），我們不可能取盡所有的點，那么這就存在一個精確性的問題。如果有一些特殊的點我們沒有取到，就會遺漏一些重要的物理性質(zhì)，因此在處理問題的時候要充分考慮MATLAB的局限性。第三，不能完全依賴MTLAB來解決物理問題。應(yīng)用MATLAB的目的是輔助大學(xué)物理的學(xué)習(xí)，加深對物理問題的理解，如果過分依賴MATLAB處理問題，反而會局限學(xué)生的思維，限制學(xué)生分析問題的能力。

用MATLAB輔助學(xué)習(xí)，將煩瑣的計算工作交由計算機來完成，并把抽象的問題具體化，可以很好地幫助學(xué)生解決在學(xué)習(xí)中遇到的困難，從而克服學(xué)生的恐懼心理，提高學(xué)習(xí)興趣。本文用質(zhì)點運動、電磁學(xué)和機械波等知識點為例，討論了用MATLAB輔助學(xué)習(xí)大學(xué)物理的方法，主要探討如何用MATLAB克服大學(xué)物理學(xué)習(xí)中的數(shù)學(xué)知識欠缺所產(chǎn)生的困難，以及用圖形的方法將物理問題具體化的過程。同時，考慮到軟件的局限性，我們也針對性地提出了應(yīng)用過程中應(yīng)注意的問題，這對學(xué)生的學(xué)習(xí)是非常有幫助的。為工科學(xué)生的大學(xué)物理學(xué)習(xí)提供了新的思路，豐富了大學(xué)物理的教學(xué)方法，對大學(xué)物理的混合教學(xué)具有一定的指導(dǎo)意義。