某邊坡巖體結構特征及變形破壞影響因素研究
0 引言
巖質邊坡的穩定性問題一直是巖土工程的一個重要研究內容,巖質邊坡的穩定性及變形破壞主要受到巖體結構面及自身強度控制,故結構面強度參數及巖體強度參數取值是巖土穩定性研究的基礎[1-2],在野外現場調查時,如何快速獲得結構面強度參數及巖體強度參數顯得尤為重要。
1 邊坡現狀
根據現場調查,某邊坡坡表植被發育,基巖裸露,坡腳落石堆積。地層巖性為板巖,節理裂隙發育,見圖1。

圖1 邊坡現狀
2 巖體結構特征
2.1 結構面強度參數取值
20世紀60年代以來,Barton與其合作者們(1973,1976)在大量天然結構面的剪切試驗的基礎上,結合結構面的幾何特征和巖體力學特性,研究了結構面抗剪強度估算方法,提出了以下的巴頓(Barton)模型[3]:

式中:JRC為結構面粗糙度系數(Joint Roughness Coefficient);JCS為結構面壁面抗壓強度(Joint Compression Strength),MPa;φb為基本摩擦角;σn為結構面上的有效正應力,MPa。
其中結構面壁面抗壓強度JCS根據回彈儀測定的Re,使用巴頓推薦的米勒經驗關系公式計算:

在計算結構面強度參數時,根據現場試驗結果,片理面基本內摩擦角取36°,節理面取32°,最大正應力取5MPa,計算結果如表1所示。

表1 基于巴頓(Barton)模型等效抗剪強度參數計算結果
通過上述計算可以得到邊坡巖體的抗剪強度為5MPa,等效粘聚力為C=0.29MPa,內摩擦角為φ=34°。

圖2 巴頓(Barton)模型的等效處理方法
2.2 點荷載試驗
點載荷試驗是利用一對端部為直徑極小的加荷錐,將巖石試樣夾在兩個錐形壓頭之間施加集中荷載,使巖石拉裂,通過計算求得試樣點荷載強度,再依據經驗關系,間接估算巖石單軸抗壓強度和抗拉強度,或者直接用于巖石分類、劃分風化帶以及評價巖石各向異性程度等[4]。
設用卡尺或儀器立柱上的標尺量得兩壓頭間距離為D,破壞荷載為P,那么點荷載強度指數為:

式中:Is為未經尺寸修正的點荷載強度指數;P為試樣破壞時的點荷載;Dc為等效巖心直徑,對巖心徑向試驗,對巖心軸向、巖塊或不規則塊試驗WD,A為過兩壓頭接觸點平面的最小截面積,W為試樣的平均寬度。
為了得到統一可比的點荷載強度值,定義巖樣經尺寸修正的點荷載強度指數Is(50)為在D=50mm巖心上進行徑向試驗所測得的值。對于在其他情況下進行的試驗,使用尺寸修正系數Kp將試驗結果歸一化為Is(50):
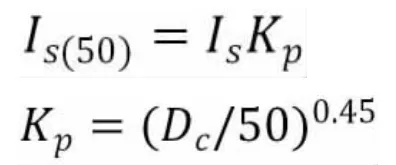
Is(50)與單軸抗壓強度σc的經驗關系:

選取邊坡坡腳處的巖石進行點荷載試驗,試驗結果見表2。
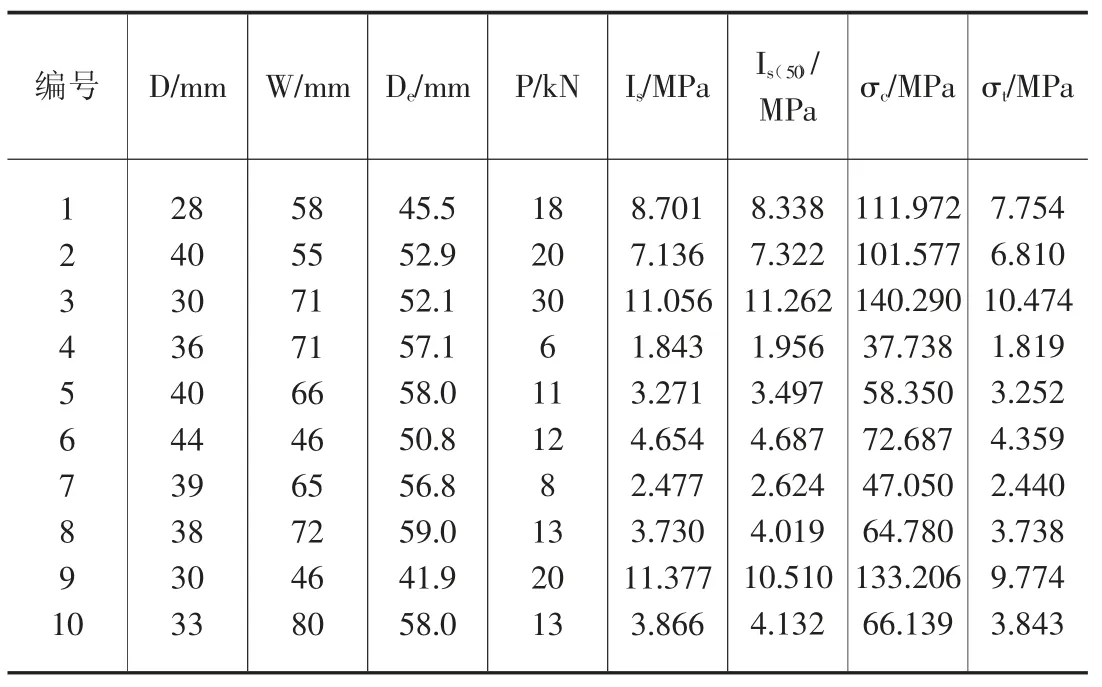
表2 點荷載試驗計算結果表
計算結果表明,巖石的平均抗壓強度約為83.379MPa,抗拉強度約為5.426MPa。
3 邊坡穩定性分析
邊坡下部出露基巖巖性為板巖,受區域地質構造和淺表生改造,以及公路施工人工開挖邊坡的影響,巖體出露部分節理裂隙發育,現場調查統計得到兩組節理,節理面J1產狀:104°∠80°,節理面J2產狀:313°∠41°,節理間距10-50cm,片理面L產狀:208°∠72°,層厚15-20cm,坡面產狀:73°∠53°。
根據巖體結構特征,赤平投影分析如圖3所示。

圖3 邊坡巖體穩定性分析圖
由邊坡穩定性分析知,圖中坡面投影區穿越單滑面1、2、3,雙滑面12、13,墜落體G,故不在邊坡面上形成滑塌體,而只有雙滑面23的滑塌形式是在邊坡臨空面出露的滑塌體。從穩定性系數分析得知,雙滑面23的穩定性系數為0.46,處于失穩滑動狀態,會產生掉塊、落石,這與現場調查結果一致。
4 邊坡變形破壞影響因素分析
本文采用離散元數值模擬軟件UDEC來模擬邊坡基巖在不同粘聚力C、內摩擦角φ下的變形破壞模式[5],其中以基巖裸露點作為邊坡位移大小d、變形速度v、最大壓應力σ的采集點。其中C取2MPa、3MPa、4MPa、5MPa、8MPa、12MPa、15MPa、18MPa、22MPa共9個不同的值,φ取0°、8°、15°、22°、30°、38°、45°共7個不同的值,兩兩結合共63種不同的模擬情況。
4.1 不同C、φ值對位移d的影響
位移大小可以直觀地反應邊坡變形的程度,位移大則邊坡變形就大,通過統計分析得到如圖4所示的點線圖。從圖中可以看出,當粘聚力C值小于8MPa時,邊坡位移波動明顯,C值越小變形差別越大;當粘聚力C值大于8MPa時,外邊坡變形趨于穩定。當內摩擦角φ值小于15°時,邊坡位移波動較大,且φ值越小變形差異越大;當內摩擦角φ值大于15°時,邊坡變形趨于穩定。綜合不同C、φ值可以看出,當C值大于8MPa且φ值大于15°時,邊坡變形趨于穩定,在0.5m-0.8m范圍內。

圖4 位移影響
4.2 不同C、φ值對變形速度v的影響
邊坡變形速度大小作為邊坡變形監測的重點,對保證工程施工和運行的安全起重要作用,將數值模擬結果統計分析得到如圖5所示的點線圖。從圖中可以看出,當粘聚力C值小于8MPa時,邊坡變形速度變化明顯,C值越小變形速度差別越大;當粘聚力C值大于8MPa時,邊坡變形速度趨于穩定。當內摩擦角φ值小于30°時,邊坡變形速度波動明顯,且φ值越小變形速度差異越大;當內摩擦角φ值大于30°時,邊坡變形趨于穩定。綜合不同C、φ值可以看出,當C值大于8MPa且φ值大于30°時,邊坡變形速度趨于穩定,在0.1m/s-0.3m/s范圍內。

圖5 速度影響
4.3 不同C、φ值對最大壓應力σ的影響
數值模擬結果表明,最大拉應力都在2MPa附近波動,這與邊坡的抗拉強度t取值為2MPa有關,故只討論在抗拉強度t為2MPa時最大壓應力的變化,通過統計分析得到如圖6所示的點線圖。從圖可以看出,最大壓應力σ隨著粘聚力C值和內摩擦角φ的增加出現線性上升的趨勢。

圖6 拉應力影響
5 結論
基于現場調查、現場試驗、數據整理、數值模擬等方法,本文得出以下結論:
①巴頓(Barton)模型是一種快速確定較硬巖體結構面強度參數的方法,在野外可以方便快速確定巖體的強度參數。
②野外應用點荷載試驗初步測試巖石的抗壓強度、抗拉強度是可行的,尤其是對于沒有條件進行現場、室內試驗的初步地質調查來說,較為實用。
③赤平投影分析結果表明,邊坡最不利滑面穩定性系數為0.46,處于失穩滑動狀態,會產生掉塊、落石,與現場調查結果一致。
④邊坡變形破壞受巖體粘聚力和內摩擦角的影響較大,當抗剪強度參數取值與現場試驗接近時,邊坡變形趨于穩定,且此時邊坡最大拉應力也與點荷載試驗結果接近。

