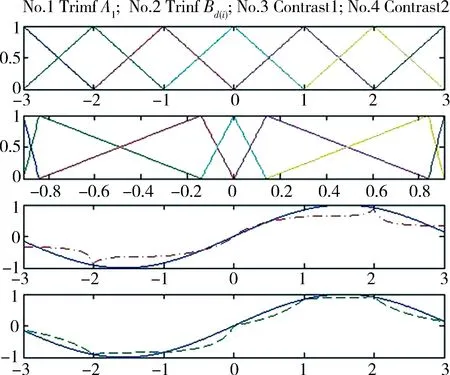
Fuzzy系統的函數逼近功能及誤差估計
李洪興
(1. 北京師范大學珠海校區 應用數學學院, 廣東 珠海 519085;2. 大連理工大學 控制科學與工程學院, 遼寧 大連 116024)
1 預備知識
熟知,Fuzzy集合是由L.A.Zadeh于1965年首次提出的,隨后,基于Fuzzy集所形成的Fuzzy推理以及使用Fuzzy推理所構造的Fuzzy系統的研究工作逐漸展開,Fuzzy系統的應用范圍逐漸擴展.其中,Fuzzy系統的函數逼近功能是一個十分有意義的研究方向.從數學的觀點看,一個Fuzzy系統實際上是從輸入論域到輸出論域的一個映射; 特別,當輸入論域和輸出論域都是實空間時,該Fuzzy系統就是一個實函數,它當然可以近似逼近某個實函數.文獻[1]已經顯示了Fuzzy系統函數逼近的雛形,文獻[2]證明了Fuzzy系統的插值機理,而文獻[3]揭示了Fuzzy系統的概率論意義.本文將從Fuzzy系統的具體構造出發討論Fuzzy系統的函數逼近功能,同時還要研究這種函數逼近的誤差估計.
值得指出的是,許多文獻也在討論Fuzzy系統的泛逼近性,但是它們都是基于所謂簡略推理法得到的非含參積分形式的推理結果,這樣的推理結果是不合理的,也是不準確的.而本文的推理結構是源于條件數學期望得到的推理結果,是一種最小二乘最優的推理結果.
2 Fuzzy系統的結構
首先,考慮單輸入單輸出的開環靜態系統,即SISO,如圖1所示.

圖1 SISO靜態開環系統
s:X→Y,
xy?s(x),
(1)
對于一個不確定性系統,常常可以通過實驗或檢測得到一組輸入輸出數據,記為
IOD?{(xi,yi)∈X×Y|i=0,1,…,n},
成為該系統的基礎數據集.根據IOD可以得到一個離散的映射
s1:X0→Y0,
xis1(xi)=yi,
i=0,1,…,n,
這里
X0={x0,x1,…,xn},Y0={y0,y1,…,yn}.
s:X→Y,
xy=s(x).
x
(2)
‖s‖?‖s‖∞?max{|s(x)||x∈X}.
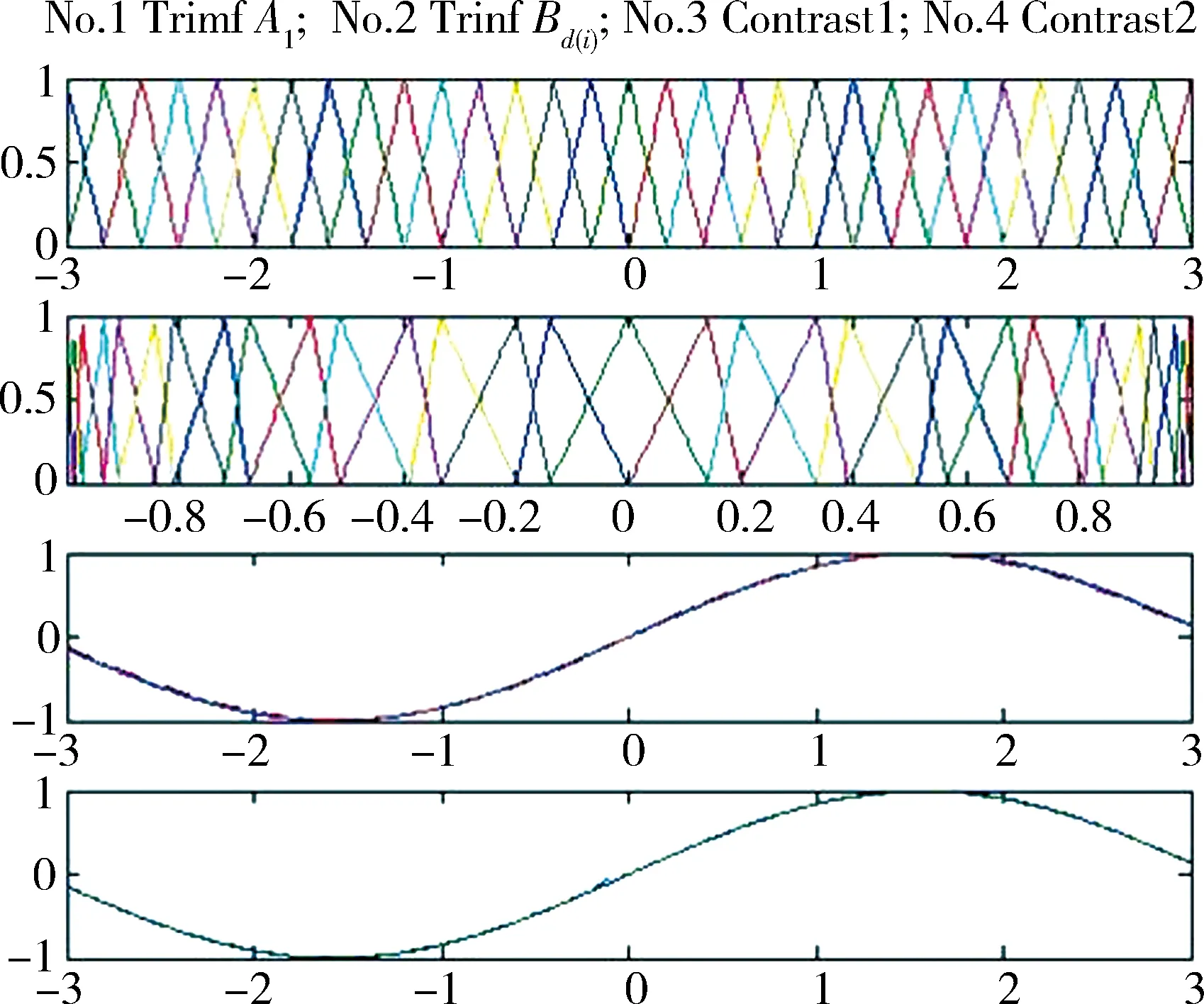
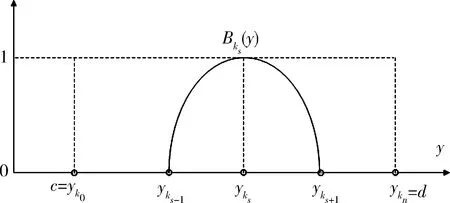
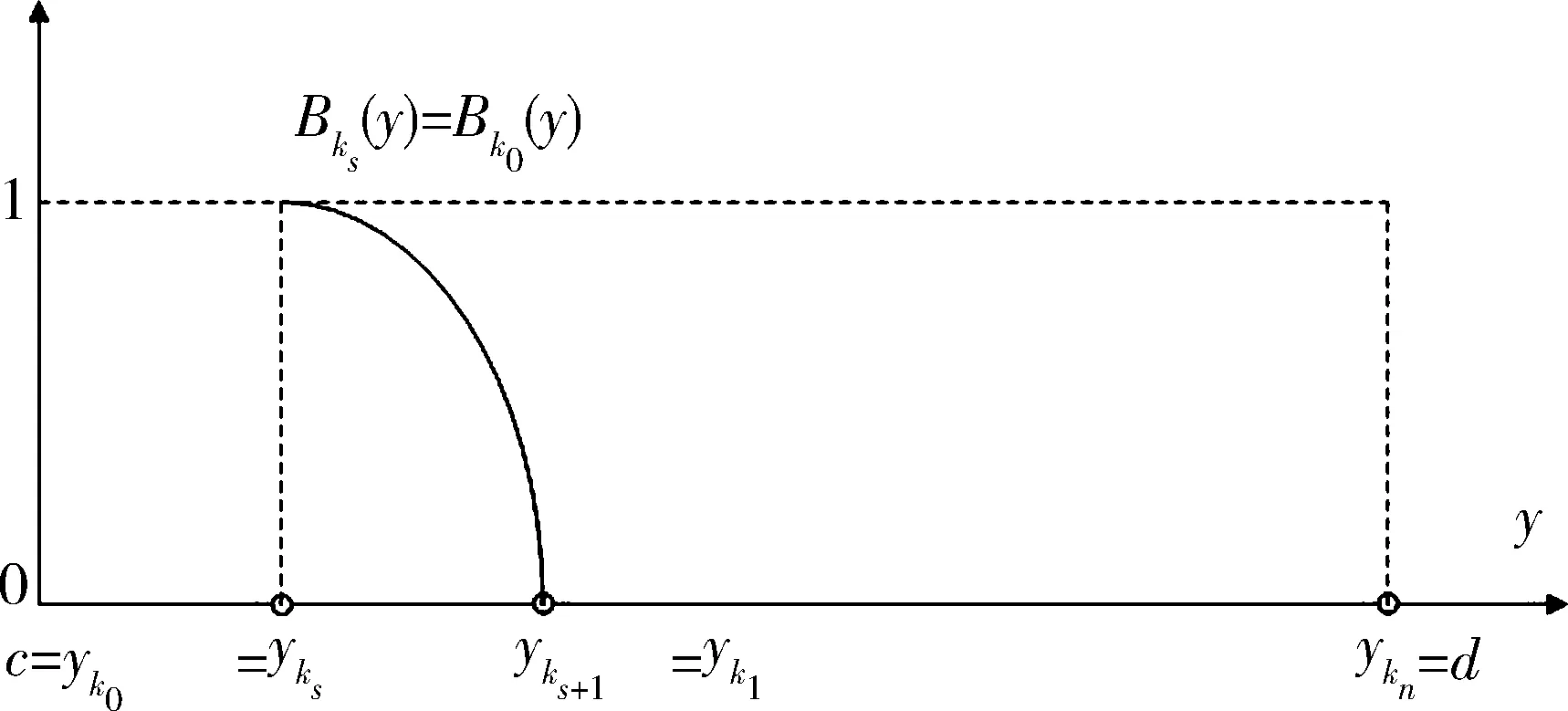
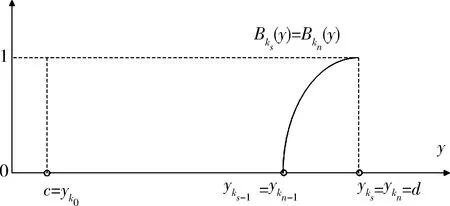
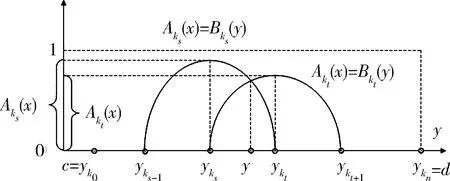
a=x0 c=yk0≤yk1≤…≤ykn=d, σ:{0,1,…,n}→{0,1,…,n}, iσ(i)=ki, (3) 或者記為 如果沒有如此的置換,如下的輸出數據集 Y0={yi|i=0,1,…,n}, 一般不滿足如下的全序關系 c=y1 Bi∈F(Y),i=0,1,…,n 時是必不可少的條件. A?{Ai|i=0,1,…,n}. 類似地,采用輸出數據集Y0也好獲取另一組Fuzzy集 B?{Bki|i=0,1,…,n}. kσ-1(i)=i, 從而Bi=Bkσ-1(i),這樣一來,便得到 B={Bi|i=0,1,…,n}. IfxisAithenyisBi,i=0,1,…,n, (4) 這里Ai和Bi分別是定義在X和Y上的Fuzzy集,即 Ai∈F(X),Bi∈F(Y), i=0,1,…,n. Ri∈F(X×Y), ?(x,y)∈X×Y, μRi(x,y)?θ(μA(x),μB(y)), 這里 θ:[0,1]×[0,1]→[0,1] ∧:[0,1]×[0,1]→[0,1], (a,b)∧(a,b)=a∧b. ·:[0,1]×[0,1]→[0,1], (a,b)·(a,b)=a·b. Fuzzy推理規則組(4)被視為如下的一個映射 s*:A→B, Ais*(Ai)?Bi, i=0,1,…,n. ?(x,y)=X×Y, μ s**:F(X)→F(Y), AB=s**(A)?A·R, μ 接下來,為了獲得如下的函數 x s**:F(X)→F(Y), s1:X→F(Y), xs1(x)?s**({x}), (5) ?(x,y)∈X×Y, μs1(x)(y)=μs**({x})(y)= μ (6) B(ξ=x)?s1(x), ?(x,y)∈X×Y, μB(ξ=x)(y)=μs1(x)(y)= (7) y=(y(ξ))ξ=x=y(x), 文獻[3]已經證明了常用的清晰化方法,即重心法是合理的,并且是在最小二乘意義下是最優的方法.現在假定 使用重心法便有需要的這個點的表達式 y=(y(ξ))ξ=x= (8) 這意味著已經得到 x (9) 然后,把(7)式帶入到(9)式中,便有 (10) 注 2.1注意到?(x,y)∈X×Y,有 μB(ξ=x)(y)=μR(x,y), (11) IOD={(xi,yi)∈X×Y|i=0,1,…,n}, Δyki=yki+1-yki,i=0,1,…,n-1, Δy 由于 Δyi=Δykσ-1(i), (12) 這里已置 μ i=0,1,…,n. (13) μ i,j∈{0,1,…,n}. 構造如下的函數 f (14) 顯然 f 特別地,當Δyi=h(i=0,1,…,n),即 Y0={yi|i=0,1,…,n} 是等距分割的數據集時,其中通用的間隔h>0,并且不難驗證滿足條件 那么有 μ i=0,1,…,n. (15) 進一步,(12)和(14)式可以簡化為 (16) f FIOD? {(Ai,Bi)∈F(X)×F(Y)|i=0,1,…,n}, 如果它滿足條件 μAi(x)∈C(X),μBi(y)∈C(Y), i=0,1,…,n, ?i∈{0,1,…,n-1},μAi(x)+μAi+1(x)=1; ?j∈{0,1,…,n-1},μBj(x)+μBj+1(x)=1. Ai(x Bi(y 注 2.2不難驗證,當FIOD具有二相性時,前面得到的結論仍然有效. 回過頭來,再考察數據集 IOD={(xi,yi)∈X×Y|i=0,1,…,n}. 引入記號 Δxi?xi+1-xi,i=0,1,…,n-1, 顯然 反之不然,即 yi=s(xi), FIOD= {(Ai,Bi)∈F(X)×F(Y)|i=0,1,…,n}. (17) 這里假定滿足條件 yi=s(xi), (18) 引理 3.1設f(x,y)是X×Y上的一個二元連續函數,其中 X=[a,b],Y=[c,d], 對于下面的含參積分 c=y0 只要 (19) 證明倘若不然,那么?ε>0,取 δk=1/k,k=1,2,…, c=y(k)0 同時存在 ξ(k)i∈[y(k)i,y(k)i+1],i=0,1,…,n-1, 盡管 λ 但是 |I(xi|≥ε. x 因為 δ 所以必有 0<ε≤ 這顯然是個矛盾,故引理為真. 引理 3.2設f(x,y)∈C(X×Y),這里 X=[a,b],Y=[c,d]. 如果?x∈X,I(x)>0,則?δ>0,使得關于Y的任何一個分割 c=y0 以及任意選取的ξi∈[yi,yi+1],如下的I(x)的Riemann和式一定滿足下面的蘊涵式 (20) 證明首先,不難理解下式 I(x)≥I(x0) 為真.今取 ε=I(x0), c=y0 以及任意選取的ξi∈[yi,yi+1],如下的I(x)的Riemann和式必滿足結果:只要 I(x0)-ε=0. 因此引理的結論為真. 再從引理 3.1和引理3.2,可以獲得如下的引理3.3. 引理 3.3設f(x,y)、g(x,y)是兩個定義在論域X×Y上的連續函數,這里 X=[a,b],Y=[c,d], c=y0 如果 (21) 證明根據引理3.2,下面的表達式對于較大的n∈N+是有意義的: 根據極限運算規則,即商的極限等于極限的商,再利用引理3.1,便知引理3.3正確. 定理 3.1關于數據集IOD,假定如下的Fuzzy數據集滿足二相性 FIOD= {(Ai,Bi)∈F(X)×F(Y)|i=0,1,…,n}. 這里滿足條件 證明對于任意給定的s∈C[a,b],假定數據集IOD滿足插值條件:?i∈{0,1,…,n}, yi=s(xi). n>N1?‖f ‖s-fn‖ fn(x)=μ 由二相性可知 μ 因此得到 |s(x)-fn(x)|= 由此便有 |s(x)-fn(x)|≤ 即 ‖s-f 取 N=max{N1,N2}∈N+, 定理 4.1在定理3.1的條件下,對于任意的函數s∈C2[a,b],假定滿足條件:?i∈{0,1,…,n-1}, μAi,μAi+1∈C2[xi,xi+1]. yi=s(xi), 則必有下面的結論: rn(x)=s(x)-fn(x)= (22) 其中 x∈[xi,xi+1],ξi∈(xi,xi+1), i=0,1,…,n-1, 2s′(ξ s(ξ qi(x)=μAi(x)Δyi+μAi+1(x)Δyi+1. ‖rn‖∞=‖s(x)-fn(x)‖ (23) 其中 Δ Ci?min{qi(x)|x∈[xi,xi+1]}, M M M L1i?max L2i?max 證明1)?x∈[a,b],當 x=xi,i=0,1,…,n, 結論顯然為真;故只考慮 x≠xi,i=0,1,…,n x∈(xi,xi+1), f μ (24) 其中 pi(x)?μAi(x)s(xi)Δyi+ μAi+1(x)s(xi+1)Δyi+1, (25) qi(x)?μAi(x)Δyi+μAi+1(x)Δyi+1. (26) f qi(x)>0. 接下來考慮逼近余項的表達式 rn(x)=s(x)-f 將它改寫為 rn(x)qi(x)=s(x)qi(x)-fn(x)qi(x)= s(x)qi(x)-pi(x), (27) 根據插值條件可知 rn(xj)=0,j=i,i+1, 或者寫為 s(xj)qi(xj)-pi(xj)=0, j=i,i+1. rn(x)qi(x)=k(x)(x-xi)(x-xi+1), (28) 進而寫為 rn(x)qi(x)=k(x)(x-xi)(x-xi+1)= s(x)qi(x)-pi(x), 事實上,設x是個固定點,構造一個輔助函數 φi(t)=s(t)qi(t)-pi(t)- k(x)(t-xi)(t-xi+1), (29) φi(xj)=0,j=i,i+1, xi 為了方便起見,引入符號: φi(t)=φi1(t)-φi2(t)-φi3(t), φi1(t)?s(t)qi(t), φi2(t)?pi(t), φi3(t)?k(x)(t-xi)(t-xi+1). 于是便有: rn(x)=s(x)-f i=0,1,…,n-1. |(x-xi)(x-xi+1)|≤ Ci=min{qi(x)|x∈[xi,xi+1]}. 最后,根據余項表達式便有如下的不等式 r Δyi=s′(ξi)Δxi, 即 Δyi?c·Δxi, ‖rn‖ 推論 4.1在定理4.1中,如果諸Fuzzy集Ai(i=0,1,…,n)具有三角波形隸屬函數,則: 1) fn(x)關于s(x)逼近的余項表達式呈現為 rn(x)=s(x)-fn(x)= i=0,1,…,n-1, (30) qi(x)=Ai(x)Δyi+Ai+1(x)Δyi+1, (ξi(x)-x 2) fn(x)關于s(x)逼近的誤差估計表達式呈現為 ‖rn‖ (31) 證明首先,容易了解一個事實:?i∈{0,1,…,n-1}, 又有 r 最后可得 M 定理 5.1在定理3.1的條件下,任取連續函數s∈C[a,b],記 μBi(y),μBi+1(y)∈C1[yi,yi+1], yi=s(xi), 則有 (32) 其中 證明對于任意選取x∈X=[a,b],有下面的表達式 |f 接下來,分別考慮下面兩個表達式的估計: μAks(x)+μAkt(x)=1, ?i?{s,t},μAki(x)≡0. 由此便有 (μAkt(x)·μBkt(y)))dy- μAks(x)yksΔyks-μAkt(x)yktΔykt|. 圖2 s=t,0 Bks(y)?μBks(y). 圖3 s=t,s=0 Bk0(y)?μBk0(y). 圖4 s=t,s=n Bkn(y)?μBkn(y). 類似地有 圖5 0 因為所有的Bki都是Fuzzy數,所以在 μAks(x)μBks(y),μAkt(x)μBkt(y) ηs-1∈(yks-1,y 使得 圖6 0=s μAks(x)yksΔyks-μAkt(x)yktΔykt|≤ 圖7 0 μAks(x)yksΔyks-μAkt(x)yktΔykt|≤ 圖8 |s-t|>1,0 圖9 |s-t|>1,0=s 圖10 |s-t|>1,0 μAks(x)yksΔyks-μAkt(x)yktΔykt|≤ μAks(x)yksΔyks-μAkt(x)yktΔykt|≤ 綜合上述的3種情形,有 μAks(x)+μAkt(x)=1. 于是有 μAks(x)Δyks-μAkt(x)Δykt|. 綜合上述3種情形,有 最后,根據1)和2)的結果,有 于是便有 這就完成了定理的證明. 推論 5.1在定理5.1中,當所有的Bi具有三角波形式的隸屬函數式,則(32)式中的Γ轉化為 (33) 這里 根據定理4.1和定理5.1,可以得出下面的結論. 定理 5.2在定理4.1和定理5.1的結論中,如果記則有 ‖s-fn‖∞+‖f∞= ‖rn‖ (34) 考慮函數 s(x)=sinx∈C[-3,3], 不難知道 ‖s′‖∞=‖s″‖∞=1. λ=Δx 再取 μ i=0,1,…,n, 圖11 和fn(x)逼近s(x) 圖12 和fn(x)逼近s(x) 可以看出:當n=6(即使用了7條推理規則),逼近的精度較低,但是曲線的光滑性不差;當n=30(即使用了31條推理規則),逼近的精度較高并且光滑性也較好.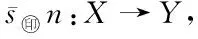
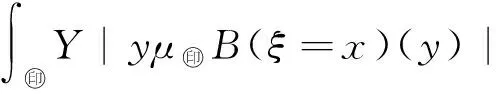
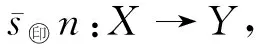
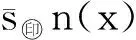
3 Fuzzy系統的函數逼近性質

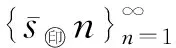
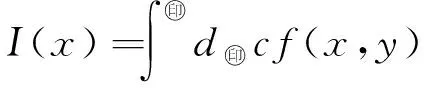
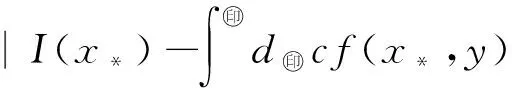
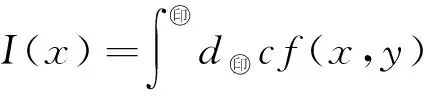

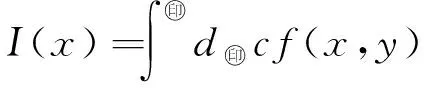
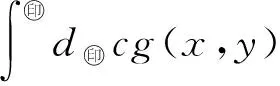
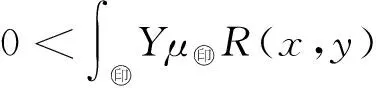
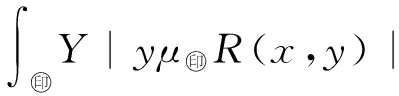
|s(x)-(μ
|s(x)(μ
(μ
μ
μ
|s(x)-s(xi)|+|s(x)-s(xi+1)|≤4 誤差分析與余項估計
5 Fuzzy系統和fn(x)之間的誤差估計
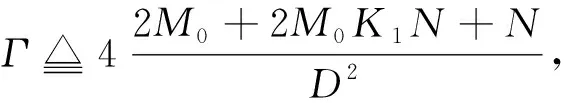
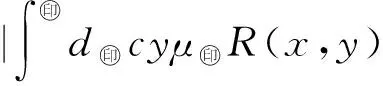
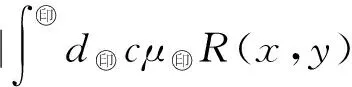
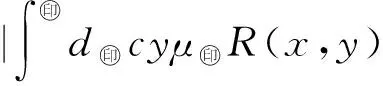
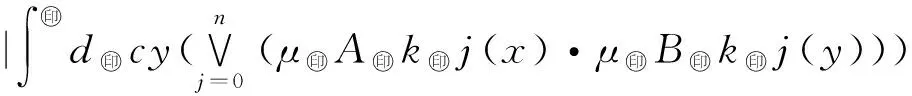
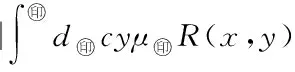
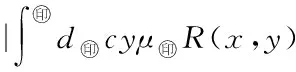
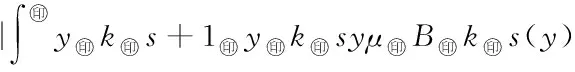
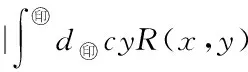
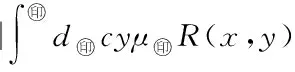
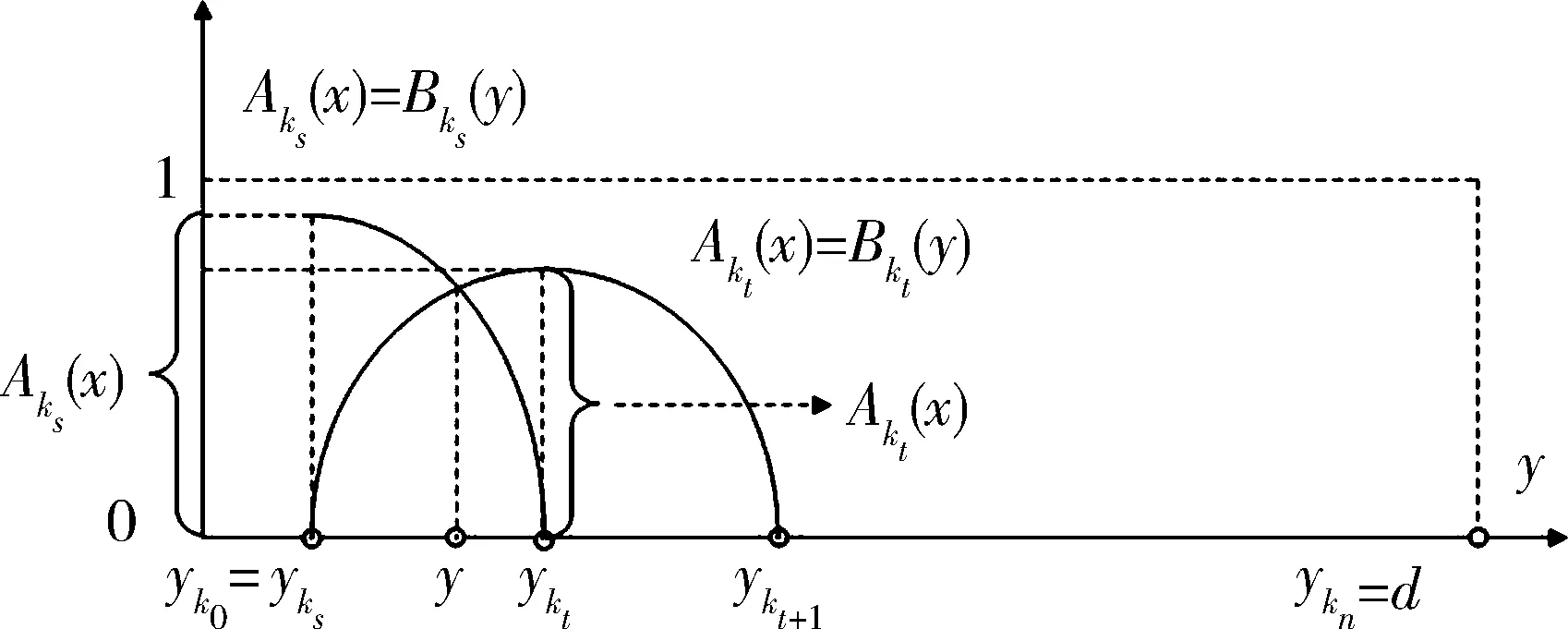
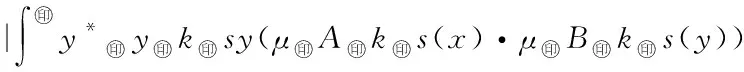
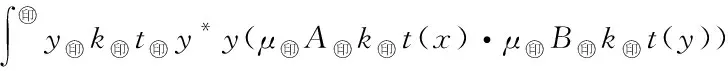
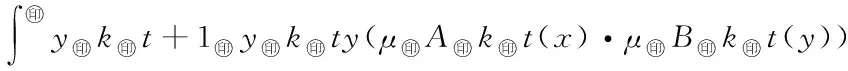
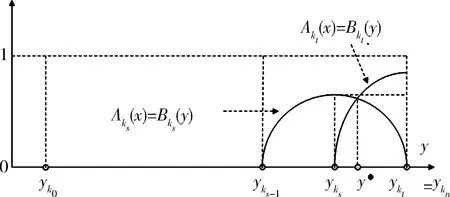

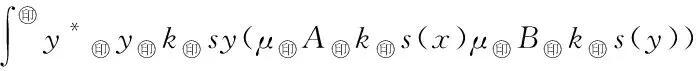
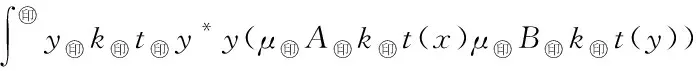
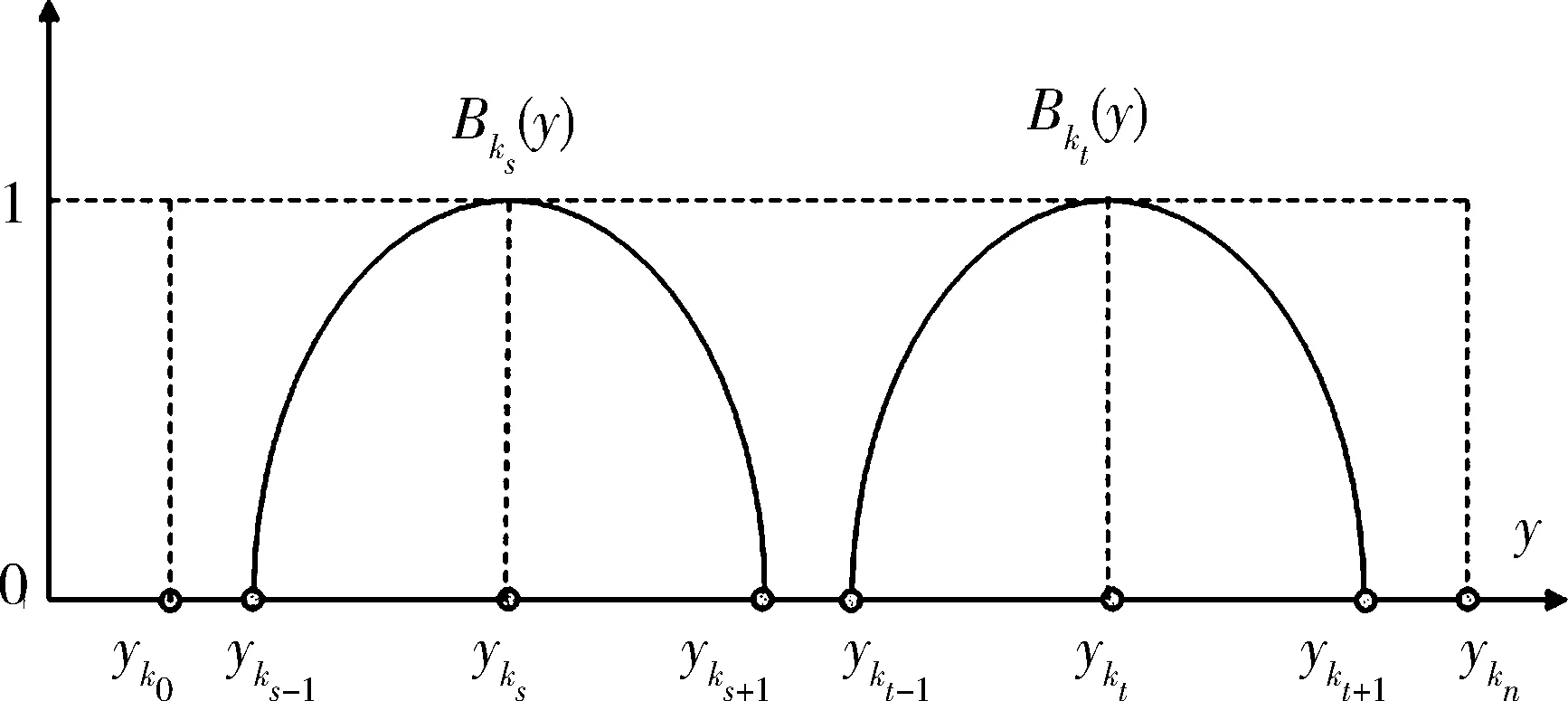
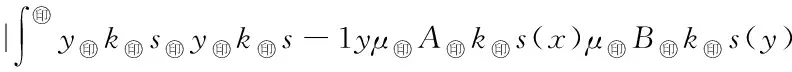
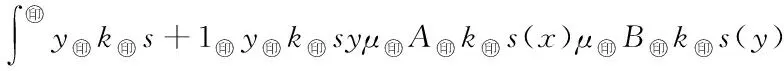
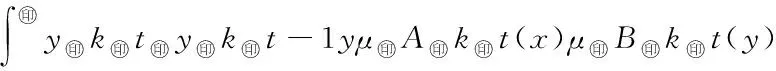
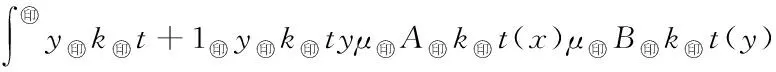
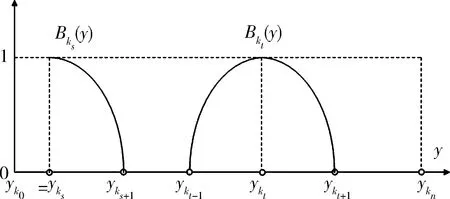
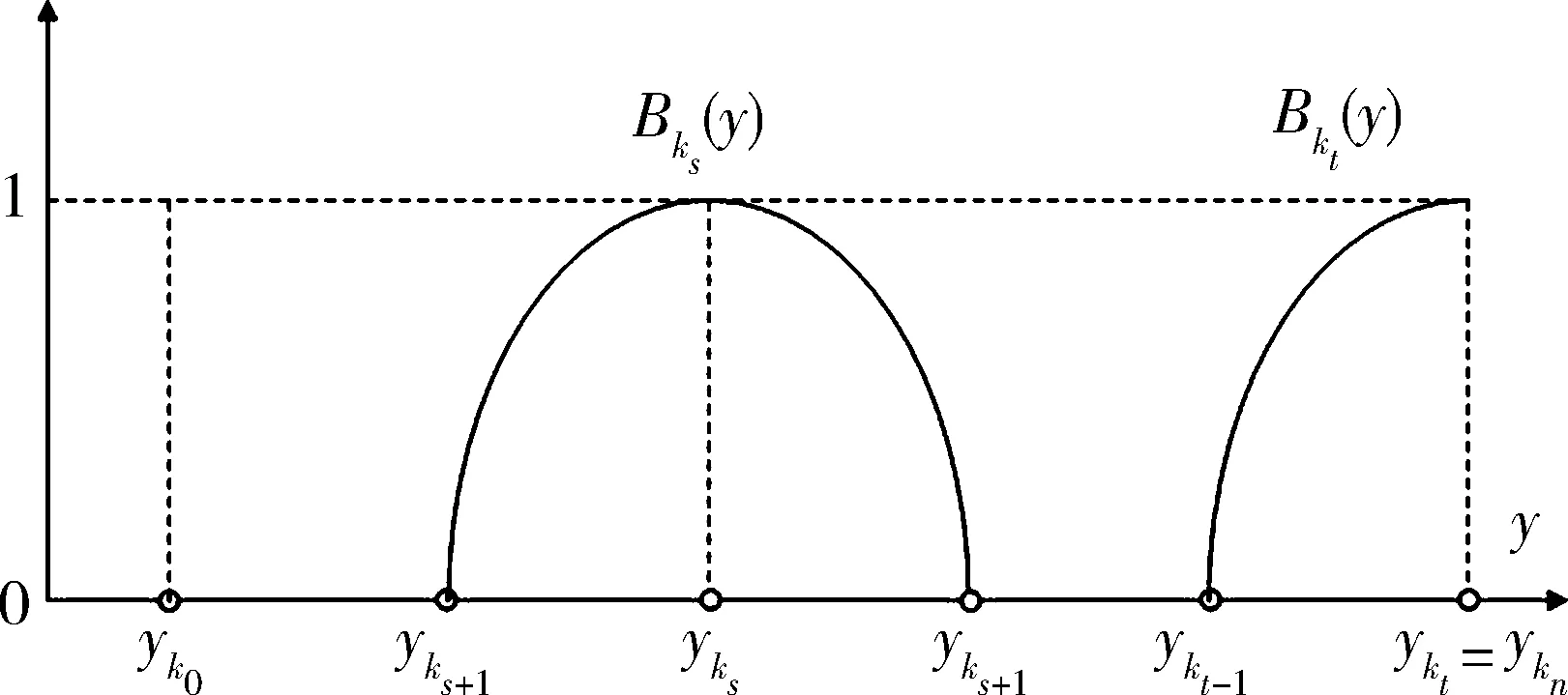
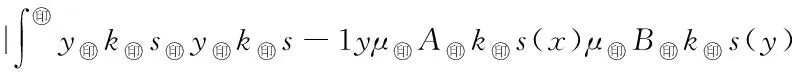
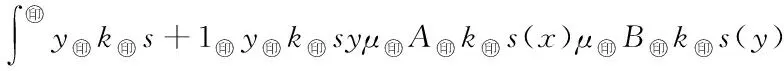
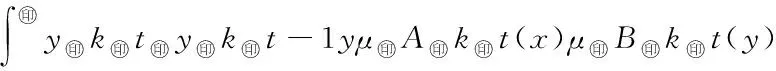
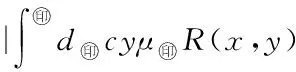
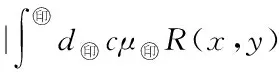
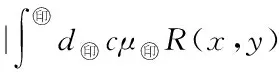
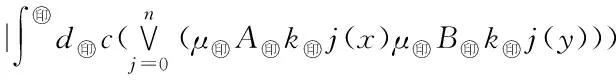
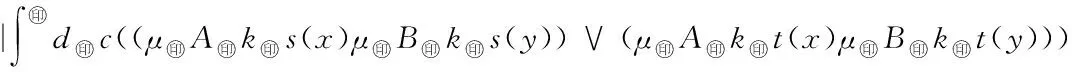
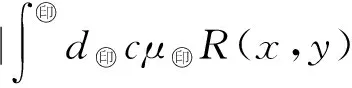
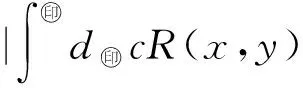
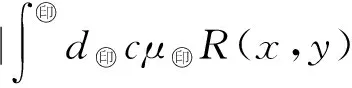
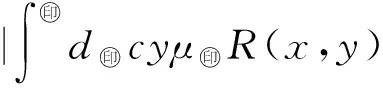
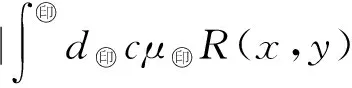
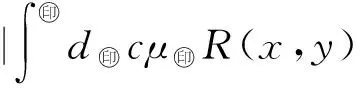
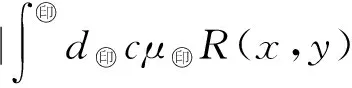
6 仿真實例