基于高斯周期的幾乎最優跳頻序列構造
周 峽, 李 燕
(南京工程學院 經濟與管理學院, 江蘇 南京 211167)
隨著現代通信的飛速發展,安全有效的通信技術已成為各行業關注的重點問題.跳頻通信由于具有抗干擾性強、頻譜利用率高、易于實現碼分多址等優點,在軍事無線電通信、衛星通信、光纖通信、水下通信、微波、雷達等多個領域中發揮著重要作用.所謂跳頻通信,是指在通信中載波頻率受偽隨機碼序列的控制而不斷跳變,從而實現頻譜擴展的一種通信系統.其中的偽隨機碼序列即跳頻序列,它對跳頻通信系統的性能起著決定性作用.隨著信息技術的發展,以及對跳頻通信的破譯技術不斷提高,需要尋找新的理想或者比較理想的跳頻序列來提高跳頻通信系統的性能.具有理想性能的跳頻序列應滿足良好的漢明自相關和互相關性、隨機性、均勻性、長周期性等特性.此外,跳頻序列的參數并不是相互獨立的,它們會受到一些理論界的限制,如Lempel-Greenberger界[1]、Peng-Fan界[2]等,因此設計達到(或逼近)這些理論界的最優(或幾乎最優)跳頻序列(族)是跳頻系統研究的重要課題之一.在本文中,討論的所有(幾乎)最優跳頻序列均是指關于Lempel-Greenberger界(幾乎)最優的.
近年來,一些學者借助組合和代數工具陸續給出了許多最優跳頻序列,詳見文獻[1,3-24].但是,對于給定的序列周期和頻率集大小,最優跳頻序列并不總是存在的.比如,參數為(5,2,2)與(6,2,3)的最優跳頻序列一定不存在[7](參數說明詳見1.1節).因此,在最優參數不存在的情形下,幾乎最優跳頻序列“等同是”最優的.然而,通信學者們也只能給出一些零散的最優參數,如何確定一般最優參數的存在性始終是未解難題.在此研究背景下,構造出更多具有新參數的幾乎最優跳頻序列也是有意義的.截止目前,關于幾乎最優跳頻序列的構造,可參考文獻[5-8,10,13,16,21,25].具體而言,2008年,Han等[25]首次提出了幾乎最優跳頻序列的概念,并通過修改已有的m-進制互素序列得到了一類幾乎最優跳頻序列.隨后,他們又借助有限域上的分圓及離散對數函數給出了另一類幾乎最優跳頻序列[5].2009年,Chung等[6]利用周期為p的M-進制序列與交織技術給出了一類具有新參數的幾乎最優跳頻序列,這里p是一個奇素數.然后,Chung等[7]分別通過拼接有限域上的分圓陪集與剩余類環上的k-重分圓[8]生成了兩類幾乎最優跳頻序列.2012年,Zeng等[10]提出了一種新的序列交織方法,并得到了五類具有新參數的幾乎最優跳頻序列.2014年,Ren等[13]借助中國剩余定理、有限域上的分圓及離散對數函數給出了幾乎最優跳頻序列的一類構造.2017年,黃波等[16]基于有限域上的分圓也給出了一類具有新參數的幾乎最優跳頻序列.最近,Xu等[21]借助中國剩余定理與Zeng-Cai-Tang-Yang廣義分圓生成了一些幾乎最優跳頻序列.綜上所得的幾乎最優跳頻序列,其參數比較詳見表1.借助有限域上的分圓和跡函數,本文構造了一類具有新參數的幾乎最優跳頻序列,此外,以這類跳頻序列為基序列,更多幾乎最優跳頻序列可通過文獻[14]中的交織技術遞歸得到.
1 基本概念
1.1 (幾乎)最優跳頻序列對于正整數l,令F={f0,f1,…,fl-1}為一個大小為l的頻率集,X={x0,x1,…,xn-1}(xi∈F,0≤i 對于跳頻序列X={x0,x1,…,xn-1},其周期漢明自相關函數定義為: H (1) 其中,如果x=y時,h[x,y]=1,否則為0.(1)式中,下標的加法運算t+τ均為模n加法. 對于跳頻序列X,定義最大周期漢明自相關值H(X)為: 本文使用記號(n,l,λ)表示大小為l的頻率集上的周期為n的跳頻序列X,且滿足H(X)=λ. 早在1974年,Lempel和Greenberger給出了H(X)的一個理論下界. 引理 1(Lempel-Greenberger界[1]) 設X是大小為l的頻率集上的周期為n的跳頻序列,則 (2) 其中,「a?表示大于或等于a的最小整數,〈n〉l為n模l的剩余類中的最小非負整數. Lempel-Greenberger界的簡化形式如下. 引理 2[19]設X是大小為l的頻率集上的周期為n的任意跳頻序列,則 (3) 其中,?a」表示小于或等于a的最大整數. 如果H(X)使得(2)或(3)式等號成立,那么稱跳頻序列X關于Lempel-Greenberger界最優;如果H(X)比(2)或(3)式右邊恰好大1,那么稱跳頻序列X關于Lempel-Greenberger界幾乎最優. Trrq(x)=x+xq+xq2+…+xqm-1,x∈GF(r). C(N,r)i={αNt+i:0≤t 加法特征具有如下正交性: (4) η(N,r) 一般情況下,高斯周期的準確值是很難決定的.本文主要用到自共軛情形下的高斯周期. η(N,r) (5) 2) 在其余情況時,有 η(N,r) 下面將利用有限域上的分圓和跡函數,構造一類具有新參數的幾乎最優跳頻序列. xt=(Trq2q(αk(q-1)t)) (7) 其中gcd(d,q-1)=1. 要證明定理1,需準備以下的3個引理: xt1=x 證明由(7)式可知 xt=(αk(q-1)t+(αk(q-1)t)q)d= (αk(q-1)t+αkq(q-1)t)d= (αk(q-1)t+α-k(q-1)t)d, 再由gcd(d,q-1)=1可知φ(x)=xd(x∈GF(q)) 是GF(q)上的一個置換.因此, xt1=xt2?(αk(q-1)t1+α-k(q-1)t1)d= (αk(q-1)t2+α-k(q-1)t2)d? αk(q-1)t1+α-k(q-1)t1=αk(q-1)t2+α-k(q-1)t2? αk(q-1)t1-αk(q-1)t2=α-k(q-1)t2-α-k(q-1)t1? αk(q-1)(t1+t2)=1? α 證明 (αk(q-1)τ-1) 因此,結論得證. η η 借助引理4~6,下面給出定理1的具體證明. 定理1的證明首先,由引理4可知序列X的頻率集大小為 HX(τ)= (8) (9) (11) (10)式是由引理5推出;(11)式是由引理6得到.因此,H(X)=2.另外, 借助定理1與文獻[14]中定理3,利用交織技術,可得到更多具有新參數的幾乎最優跳頻序列: 注以下將給出本節構造與已知相關構造的跳頻序列參數比較,如表1所示,其中這些序列關于Lempel-Greenberger界都是幾乎最優的. 表1 幾類幾乎最優跳頻序列的比較 下面給出實例分別來驗證定理1與定理2中結論. X={32,14,10,46,23,43,6,21,63,67,25,9,69, 53,45,103,0,24,82,74,58,118,102,60,64,106, 121,84,104,81,117,113,95,113,117,81,104,84, 121,106,64,60,102,118,58,74,82,24,0,103,45, 53,69,9,25,67,63,21,6,43,23,46,10,14}, 利用Magma軟件計算可得,序列X的周期漢明自相關函數 H 因此,序列X具有參數(64,33,2),且關于Lempel-Greenberger界幾乎最優,這與定理1中結論是一致的. X={2,5,4,15,14,17,14,15,4,5}, yt=(〈t0g(t1)〉n,xt1), (12) 則由(12)式定義的跳頻序列 Y= {(0,2),(2,5),(1,4),(0,15),(2,14),(2,17), (0,14),(1,15),(2,4),(0,5),(1,2),(1,5), (0,4),(2,15),(1,14),(0,17),(1,14),(2,15), (0,4),(1,5),(2,2),(0,5),(2,4),(1,15), (0,14),(1,17),(2,14),(0,15),(1,4),(2,5)}, 利用Magma軟件計算可得,序列Y的周期漢明自相關函數 {H 0,2,0,2,0,2,0,0,0,2,0,2,0,2,0,2,0}. 因此,序列Y具有參數(30,18,2),且關于Lempel-Greenberger界幾乎最優,這與定理2中結論是一致的. 本文利用有限域上的分圓和跡函數構造了一類具有新參數的跳頻序列,并通過理論和實例證明該跳頻序列關于Lempel-Greenberger界幾乎最優.同時,通過采用合適的映射和交織技術,一批具有新參數的幾乎最優跳頻序列可被遞歸得到,這些跳頻序列在碼分多址通信系統中具有廣闊的應用前景. 致謝南京工程學院校級科研基金項目(QKJ201804)對本文給予了資助,謹致謝意.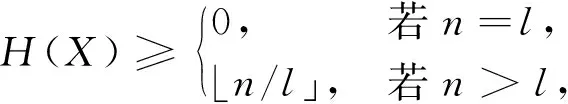

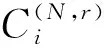


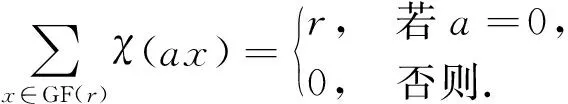




2 主要結果

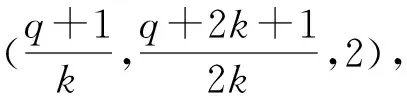









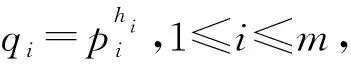

3 實例分析

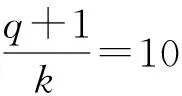
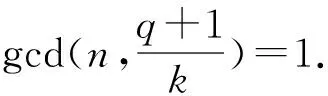
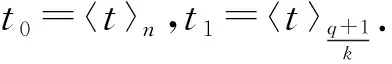
4 結束語

