HPM視角下極限概念的高效教學*

金 晶 齊 淵

（隴東學院 數學與統計學院 甘肅慶陽 745000）

以極限理論為基礎的微積分是高等院校理工科專業的公共必修課程，具有廣泛的實際應用價值和深厚的歷史文化底蘊。其中，極限概念的教學也是人們關注的焦點之一。國內外學者從心理學、方法論、辯證思想等不同的角度對極限概念教學進行了研究，但是HPM視角討論極限概念的教學，不僅提高了學生的學習興趣、幫助學生更好地理解數學本質，還可以充分發揮數學史的育人作用和價值導向，很有必要進一步研究。

一、HPM理論闡釋

1972年，第二屆國際數學教育大會上成立數學史與數學教育關系國際研究小組（International Study Group on the Relatiions between History and Pedagogy of Mathematics，簡稱HPM），該組織專門研究數學史與數學教育之間的關系，包括數學與其他學科的關系、多元文化的數學、數學史與學生的認知發展、數學史與發生教學法、數學史與學生的困難、數學原始文獻在教學中的應用等具體內容，研究的最終目的是通過數學史的運用提高數學教育教學水平。數學史中不僅包括具體的數學理論知識，還涉及數學哲學、科學哲學、社會史、文化史等內容，其中蘊含的思想、觀點、方法、意識等對于學生掌握數學知識、數學思想，培養學生的理性思維等都有不可替代的作用HPM研究的理論基礎與數學認知理論、建構主義理論、弗賴登塔爾的“再創造”等理論具有一定程度的一致性。

二、HPM視角下極限概念的高效教學

1.極限概念分析

（1）概念演變過程的分析

古希臘的“窮竭法”和我國魏晉時期劉徽的“割圓術”，都體現了直觀基礎上樸素的極限思想。16世紀開始，數學家開始改進窮竭法，大膽提出要運用極限思想思考問題。17世紀，微積分創立之后，遇到邏輯困難，牛頓試圖以 “如果當n無限增大時，an無限地接近于常數A，那么就說an以A為極限”的極限概念作為微積分的基礎，但是其中對“無限過程”的直觀描述不能作為科學論證的邏輯基礎。到19世紀，法國數學家柯西在前人工作的基礎上闡述了較嚴格的極限概念：“當一個變量逐次所取的值無限趨于一個定值，最終使變量的值和該定值之差要多小就多小，這個定值就叫做所有其他值的極限值，特別地，當一個變量的數值（絕對值）無限地減小使之收斂到極限0，就說這個變量成為無窮小。”但是該敘述中仍有“無限趨于”“要多小就多小”等直觀的描述性詞語，后來經過數學家們的努力，德國數學家魏爾斯特拉斯給出嚴格的“ε-δ”和“ε-N”定義。

（2）概念中文化素材分析

極限概念的發展歷史中，豐富的文化素材可以作為育人資源，首先是其思想萌芽，展示了我國古代輝煌的數學成就，是堅定文化自信的重要源泉；其次是其歷史背景，微積分理論基礎不牢靠讓數學家們從研究實際問題解決轉向研究數學基礎理論，極大的推動了數學自身的發展；第三是從樸素到精準、動態到靜態、特殊到一般、直觀到抽象的演進過程，深刻地詮釋了馬克思主義的立場和方法的科學性；第四是數學家的事跡，堅定的數學信念支撐他們堅忍不拔、孜孜不倦追求真理，可以培養學生嚴謹、求實的科學精神和永攀科學高峰的責任感和使命感。

2.教學方式分析

數學教學中，運用數學史的方法有附加式、復制式、順應式和重構式。本研究主要采用重構式，根據學生學習的過程與數學發展的歷史存在相似性，將數學知識逐步演化的歷史過程與數學演繹的邏輯推理過程有機地結合起來，運用數學史的觀點和材料來重構教學的體系與內容，使學生深入理解課本上形式化推理體系的真正內涵，并有效傳遞育人信息。采用這種方式，教師需要做到以下幾個方面：了解所講授主題的歷史發展過程；確定歷史發展過程中的關鍵環節，從一個環節發展到下一個環節的動因以及數學家所遇到的困難和障礙；重構這些環節，使其適合于課堂教學；設計出一系列由易至難、環環相扣的問題。

3.重構教學過程

極限概念的發生演變經歷了古代極限思想及方法——依賴直觀的描述——柯西較為完整的極限定義——嚴格的ε-δ、ε-N定義等重要環節。教材是由數列極限到函數極限，其中數列極限概念的呈現是割圓術介紹——實例引入——數列極限的描述性定義——數列極限的ε-N定義，這樣從特殊到一般的處理方法更容易歸納概括定義，但是對極限概念產生的必要性及其中蘊涵的文化要素展示不夠極限概念的教學進行重構，如圖1所示。

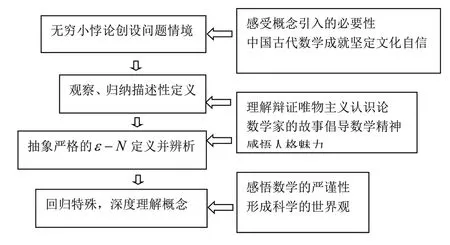
圖1 極限概念重構路徑

上圖可以看出，教學中從無窮小悖論出發結合傳統文化典例創設問題情境，引發認知沖突讓學生感受概念引入的必要性，融合數學史自然而然地展開觀察、歸納、抽象概念的活動，以能夠理性、客觀地認知相關問題，設疑、探究、釋疑過渡自然，而且融入文化元素以潛移默化地對學生進行價值塑造。

4.教學設計

（1）無窮小量引起的悖論

莊子在《天下篇》中的“一尺之棰，日取其半，萬世不竭”及劉徽的“割之彌細，所失彌少，割之又割以至于不可割，則與圓合體而無所失矣”都體現出了極限思想，尤其運用“割圓術”計算圓周率，奠定了之后千余年來中國圓周率計算在世界上的領先地位。但是“萬世不竭”和“與圓合體而無所失”總讓人感覺不可思議，為什么會這樣呢？

為了搞清楚上面的疑惑，先返回看高中數學中的函數y=f（x）在點x0的導數是先列出等式：

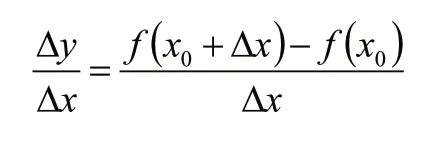
再讓 Δx趨于0這個推導過程中先承認 Δx不等于零，后又需要 Δx為零，豈不矛盾？

Δx就像是前面提到的“萬世不竭”的木棒雖然能趨于0，就是要多小有多小，卻不是0！這個可以小的比什么都小卻不一定是0的量。后來，牛頓在微積分理論中稱之為無窮小量，但這并沒有消除邏輯上的爭議。數學家們也從來不怕困難，他們堅信迷霧深處有光明。

（2）觀察、歸納描述性定義

理解極限理論的困難在于無窮，但從大家已經承認的自然數上突破就容易得多，先說明數列的概念。

如果按照某一法則，對每個n∈N+，對應著一個確定的實數xn，這些實數xn按照下標n從小到大排列得到一個序列x1,x2,x3...xn...就叫作數列，記為 {x n}。數列中的每一個數叫作數列的項，第n項xn叫作數列的一般項（或通項）。

觀察下面數列：

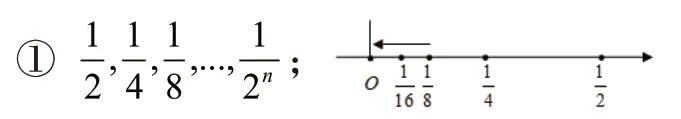
結合數軸容易觀察出，當n無限增大時，該數列在數軸上的對應點從原點的右側無限接近于0。

② A1，A2，A3，...，An；（其中，An是圓內接正3×2n邊形的面積，圓的面積記s）借助幾何直觀易知，隨著多邊形邊數的不斷增加，即當n無限增大時，An無限接近于s。

在數軸上的對應點從1的兩側無限接近于1。

一般地，可以給出下面的定義：

這個定義接近柯西的極限定義，柯西還以此為基礎定義了無窮小量：如果一個變量像這樣無限地減小，使其收斂到零，那么，我們就說這個變量是無窮小。但是，該定義中出現的“無限接近”“趨向于”等文字語言仍然難以用于嚴謹的數學推理。

（3）抽象嚴格的極限定義

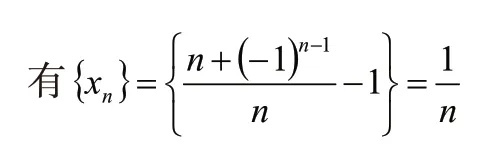
由此可見，當n增大時，1/n減少，數列的一般項接近于1。只要n足夠大，就能使1/n小于任意給定的正數，即當n無限增大時，1/n無限減少，數列的一般項無限接近于1。

在n→∞時候無限接近于1這個事的數學本質。

就這樣，基于柯西給出的定義，魏爾斯特拉斯進一步抽象地給出嚴謹的極限概念表述。

定義2 設有數列{x n}，如果存在常數A，對于任意給定的正數ε（無論它有多小），總存在正整數N，使得對于n＞N的一切xn，都有不等式成立，則稱常數A為數列{x n}。當n→∞時的極限，記為或者xn→A(n→∞)。

此時，也稱數列{x n}收斂于A，稱{x n}為收斂數列，反之稱為發散數列。

注意：正數ε具有雙重性，其任意性讓不等式表達出是個無窮小量，也就是xn與A無限接近的意思；其確定性關系到正整數N的選定。顯然，ε的任意性是通過無限多個相對確定的ε表現出來的，體現常量與變量的辯證統一。

“數列{x n}的極限是A”的幾何意義略。

為了方便表達，引入兩個記號“?、?”分別表示“任意”和“存在”，這樣數列極限的定義可以表述為：

這個簡潔、抽象的嚴格定義，讓我們看到數學家們的偉大智慧，他們突破重重困難，將極限思想轉化為數學的語言，用數學的方法描述，讓數學重新回歸理性的局面.青年學生要如這些數學家們一樣努力學習、奮發圖強，勇于探索、敢于攻關，不畏艱險永攀科學高峰，為建設科技強國貢獻自己的力量。

（4）深度理解極限概念

上面兩個極限的表述是完全脫離直觀的數學語言的表述，正是這高度的抽象性才使之應用范圍極為廣泛。

三、評價與反思

教學設計中，運用重構式教學讓學生感知數學概念產生、發展的基本過程及其中的出現矛盾沖突，激發學生的學習興趣與積極性。比如，“無窮小量”是什么，“無限接近”怎么用數學語言表述等。概念抽象時，選擇具有豐富文化內涵的經典案例，從直觀圖像和抽象符號兩方面呈現，讓學生產生內在共鳴、思維深度參，透過現象抽象出概念的本質屬性，完成概念的建構，體會辯證唯物主義認識論的正確性。同時，適當地展示歷史過程及數學家們的工作，讓學生領悟用數學的眼光看待和認識問題的思想真諦，發展智力，培養創新精神，提高提出問題、研究問題和解決問題的能力。

結語

HPM視角下的概念教學不只是簡單地講故事，更不是生硬地加入，而是站在學生認知水平和學習動機的基礎上，利用數學史這寶貴的教學資源借鑒、重演、重構數學教學中知識的呈現.真正做到傳授數學知識的同時，潛移默化地讓學生形成正確的人生觀、價值觀，實現高等數學課程的育人功能.因此，很有必要深入研究HPM視角下的高等數學教學的更多案例。