體積約束的非局部擴(kuò)散問(wèn)題基于新的技巧的有限元方法

葛志昊, 吳慧麗

(河南大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，開(kāi)封 475004)

0 引言

連續(xù)介質(zhì)力學(xué)中的非局部理論是由文獻(xiàn)[1–3]提出的。近場(chǎng)動(dòng)力學(xué)模型和非局部擴(kuò)散模型都屬于非局部理論的范疇，自Silling 在文獻(xiàn)[3]中首次介紹近場(chǎng)動(dòng)力學(xué)模型之后，其有效性已經(jīng)在許多領(lǐng)域得到證明，如復(fù)合材料的斷裂、多晶體的斷裂、納米纖維網(wǎng)絡(luò)、裂縫的不穩(wěn)定、圖像處理等[4–6]。非局部模型是一個(gè)不涉及位移場(chǎng)空間導(dǎo)數(shù)的積分型方程，因此，非局部模型允許有跳躍間斷點(diǎn)的解存在，并且可以用同一個(gè)非局部方程來(lái)描述間斷點(diǎn)及非間斷點(diǎn)處的物理過(guò)程，而不需要知道間斷點(diǎn)的位置。此外，可以將非局部模型看作分子動(dòng)力學(xué)的變形，它可以從微觀上反映物理材料中粒子之間的相互作用，將連續(xù)力學(xué)與分子動(dòng)力學(xué)聯(lián)系起來(lái)[7]，克服了經(jīng)典的連續(xù)模型只能從宏觀的角度研究材料的結(jié)構(gòu)性質(zhì)和影響規(guī)律的缺點(diǎn)。對(duì)于近場(chǎng)動(dòng)力學(xué)模型Cauchy 問(wèn)題的適定性研究，可以參考文獻(xiàn)[8–11]。特別是，文獻(xiàn)[10,12]提出了一種非局部向量微積分計(jì)算和抽象的非局部平衡法則。此外，也有一些數(shù)值方法求解該問(wèn)題，包括分片常數(shù)有限元方法、有限差分法、求積法和質(zhì)點(diǎn)法等[13–16]。最近，文獻(xiàn)[17]提出了分片常數(shù)有限元方法來(lái)解決非局部擴(kuò)散問(wèn)題。為了得到一種高階數(shù)值方法，我們提出了一種高階有限元方法來(lái)求解二維體積約束的非局部擴(kuò)散問(wèn)題，并采用一種新技巧計(jì)算線性元的剛度矩陣。值得一提的是，求解二維體積約束的非局部擴(kuò)散問(wèn)題并不是平凡的。

本文第1 部分，我們提出了體積約束的非局部擴(kuò)散問(wèn)題的有限元方法，給出了元素的編碼原理和數(shù)值計(jì)算節(jié)點(diǎn)的編碼表達(dá)式。此外，我們還采用了一種新的方法來(lái)計(jì)算剛度矩陣。最后，通過(guò)數(shù)值算例驗(yàn)證了理論計(jì)算結(jié)果。

1 基于新技巧的有限元方法

令? ?Rd(d= 2,3)表示一個(gè)有界連通開(kāi)區(qū)域，且?=?s ∪?I，其中?s是解區(qū)域，?I是?s周?chē)鷮挾葹棣牡南拗茀^(qū)域。現(xiàn)在，我們列出了一些如下的符號(hào)，關(guān)于定義的細(xì)節(jié)和一些例子，可以參考文獻(xiàn)[12]。

β=β(x,x′):?×? →R 為一個(gè)兩點(diǎn)標(biāo)量函數(shù)，并且滿足：

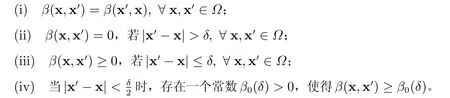
注意，δ/2 可以用其他小于δ的適當(dāng)?shù)某?shù)來(lái)代替，以保證β(x,x′)的非退化性。

令α=α(x,x′) :?×? →? ≤Rd是一個(gè)反對(duì)稱兩點(diǎn)向量函數(shù)滿足α(x,x′)+α(x′,x) = 0。給定一個(gè)兩點(diǎn)函數(shù)v :?×? →? ?Rd和一個(gè)點(diǎn)函數(shù)u:? →R，非局部散度算子D(v):? →R 和其共軛算子D?(u):?×? →? ?Rd，定義如下

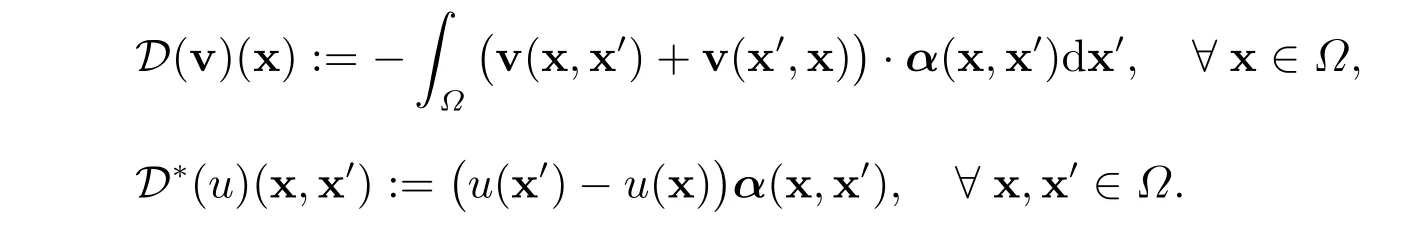
本文研究帶有體積約束的非局部擴(kuò)散問(wèn)題

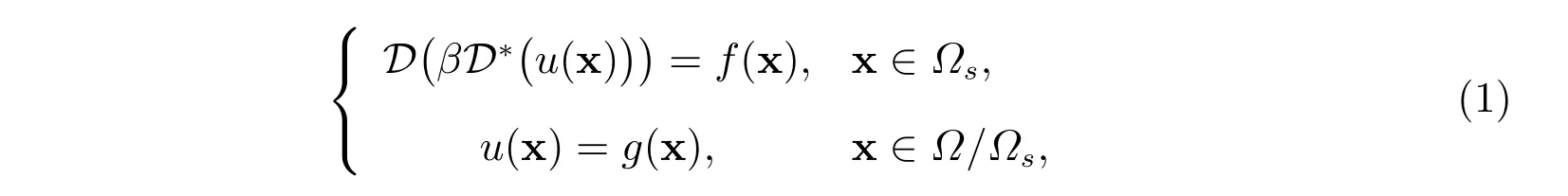
其中?=(?δ,1+δ)×(?δ,1+δ),?s=(0,1)×(0,1)。

問(wèn)題(1)中的核函數(shù)用γ(x,y)來(lái)表示，即γ(x,y)=βα·α。若取

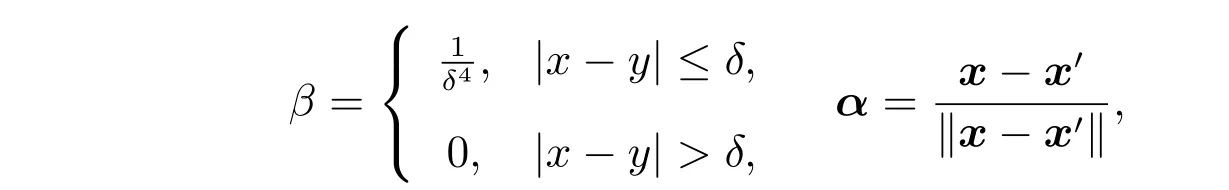
則有

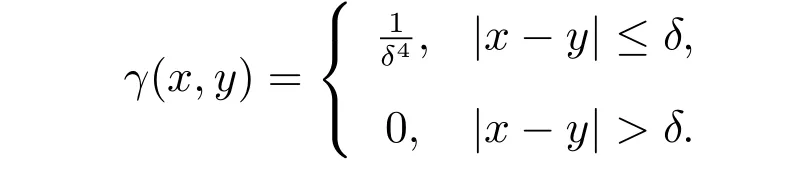
將區(qū)域?s剖分成2N1N2(N1=N2=N)個(gè)三角形單元，從而得到步長(zhǎng)

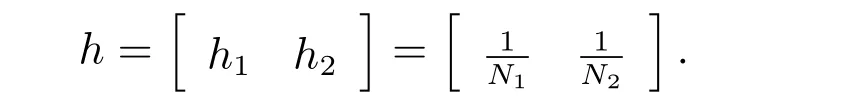
同時(shí)，以相同的步長(zhǎng)對(duì)帶狀邊界區(qū)域?/?s進(jìn)行剖分，將區(qū)域?上的三角形剖分單元的集合記為P=∪{K}=P1∪P2，其中K為三角形剖分單元，P1是求解區(qū)域?s上三角形剖分單元的集合，P2是帶狀邊界區(qū)域上?/?s三角形剖分單元的集合。

記?上有限元節(jié)點(diǎn)的指標(biāo)集為N，?s上的有限元節(jié)點(diǎn)指標(biāo)集為NI，?/?s上有限元節(jié)點(diǎn)的指標(biāo)集為Nb，求解區(qū)域?s上的有限元節(jié)點(diǎn)總數(shù)為n= (N1+1)(N2+1)，區(qū)域?上有限元節(jié)點(diǎn)總數(shù)為n1。

設(shè)P和T分別是2×n和3×(2N1N2)的矩陣，矩陣P的第k列表示三角形剖分中整體編碼是k的節(jié)點(diǎn)的坐標(biāo)，矩陣T的第k列表示三角形剖分中編碼是k的三角形剖分單元的三個(gè)頂點(diǎn)對(duì)應(yīng)的整體編碼。剖分節(jié)點(diǎn)的整體編碼按照由左至右、由下至上的原則，三角形剖分單元上三個(gè)節(jié)點(diǎn)的局部編碼按照逆時(shí)針的原則。例如，N1=N2= 2 時(shí)，每個(gè)三角形剖分單元上剖分節(jié)點(diǎn)的局部編碼如圖1，剖分節(jié)點(diǎn)以及三角形剖分單元的整體編碼如圖2。

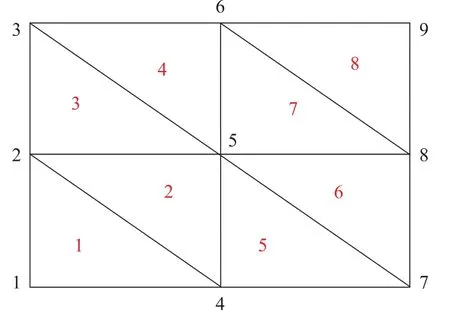
圖2 剖分單元及節(jié)點(diǎn)的整體編碼

下面采用線性有限元方法來(lái)求解非局部擴(kuò)散問(wèn)題(1)，V和V h ?V分別是非局部擴(kuò)散問(wèn)題(1)的解空間及有限元子空間。在參考三角形單元上三個(gè)頂點(diǎn)對(duì)應(yīng)的節(jié)點(diǎn)局部基函數(shù)分別為

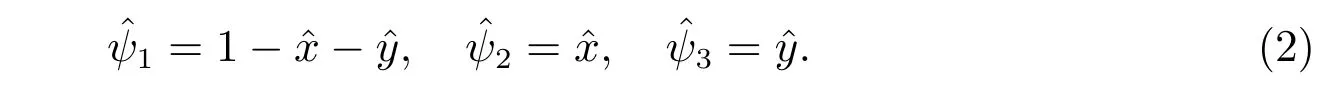
令A(yù)m1=(xm1,ym1)′,Am2=(xm2,ym2)′,Am3=(xm3,ym3)′。然后，根據(jù)參考單元與實(shí)際單元Km=△Am1Am2Am3之間的仿射變換關(guān)系式(2)，我們可以定義實(shí)際三角形剖分單元Km上三個(gè)節(jié)點(diǎn)對(duì)應(yīng)的局部基函數(shù)ψmi(x,y)=,i=1,2,3，其中

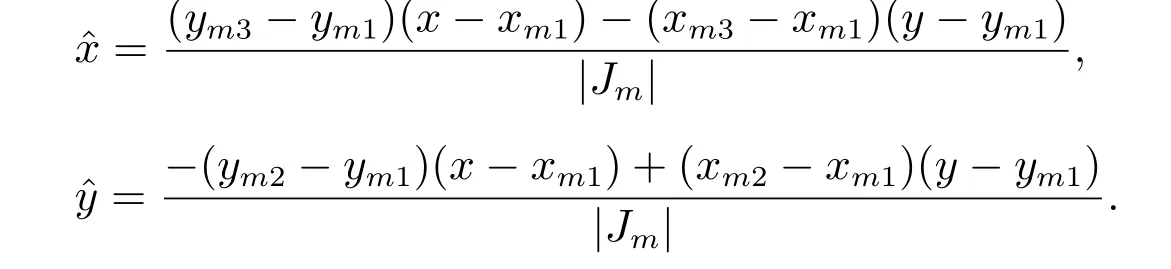
|Jm|=(xm2?xm1)(ym3?ym1)?(xm3?xm1)(ym2?ym1)為Jacobi 矩陣的行列式。因此，整體線性基函數(shù)?i滿足

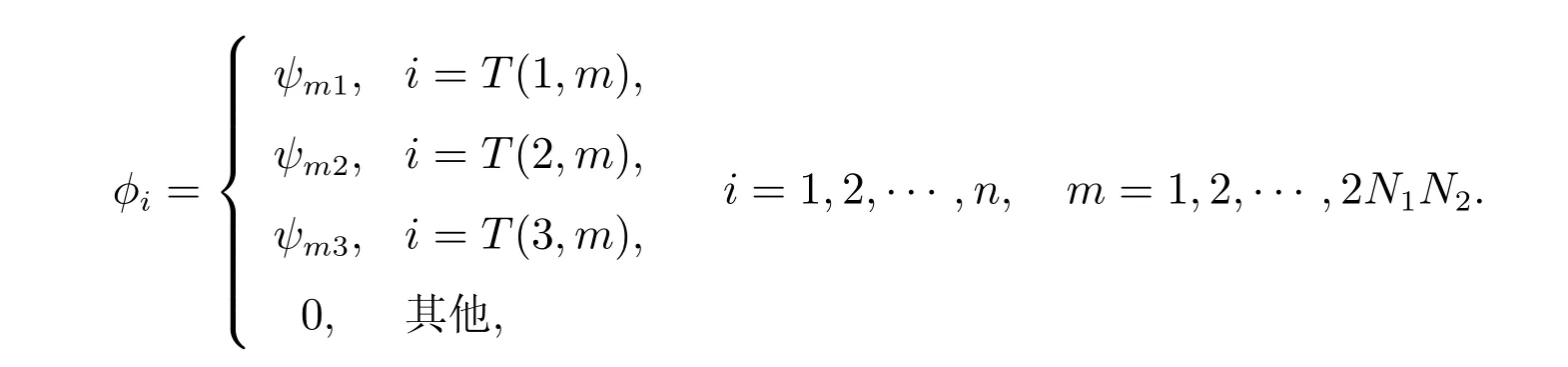
記?i??i(x)，則非局部擴(kuò)散問(wèn)題(1)的變分形式及有限元逼近的一般形式分別是：求u(x)∈V和uh(x)∈V h，使得

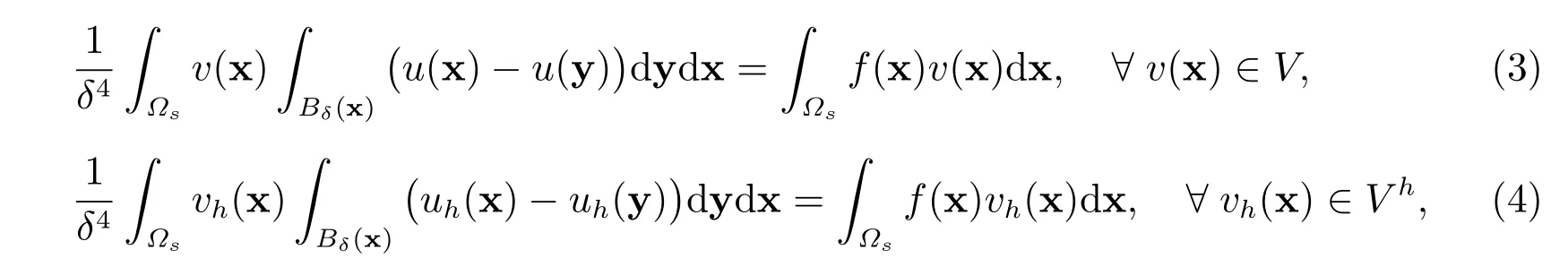
其中

uj表示在節(jié)點(diǎn)xj處的數(shù)值解的值。

令v(x)=?i(x),i ∈NI，并且利用式(4)，則有

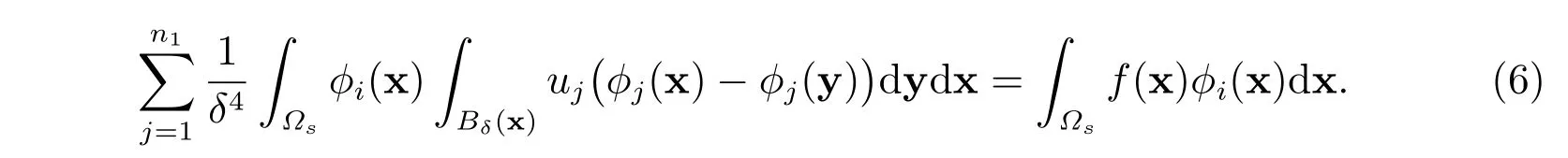
因此，有

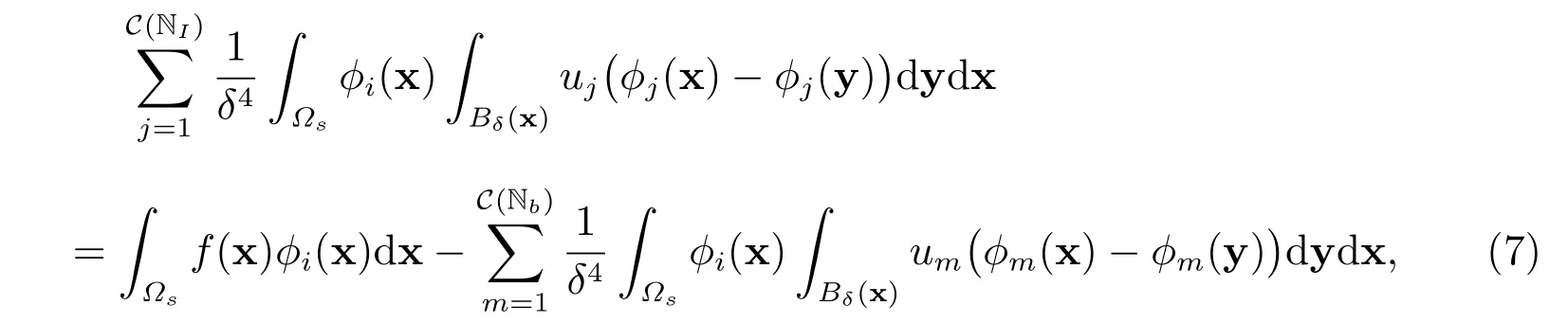
其中C(NI)和C(Nb)分別是NI和Nb索引集的元素的個(gè)數(shù)，i,j ∈NI,m ∈Nb。然后，得到線性代數(shù)系統(tǒng)

其中剛度矩陣A 為

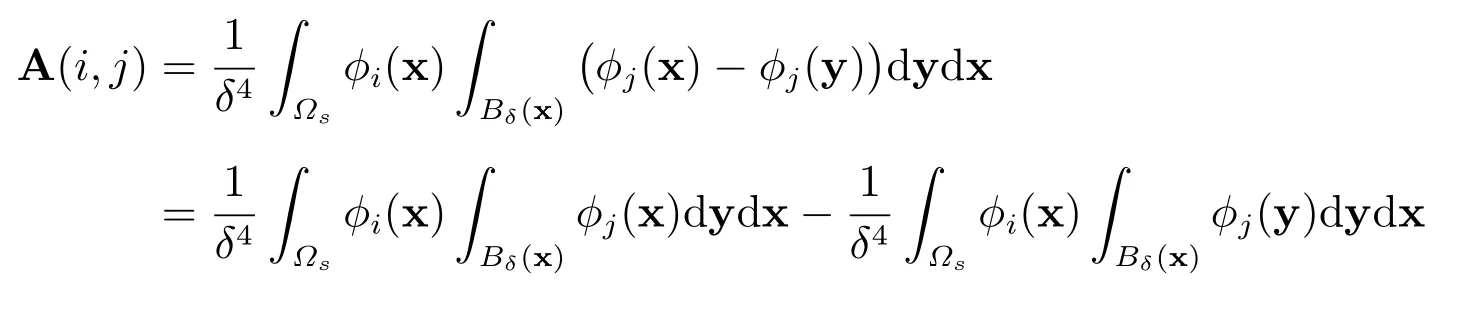
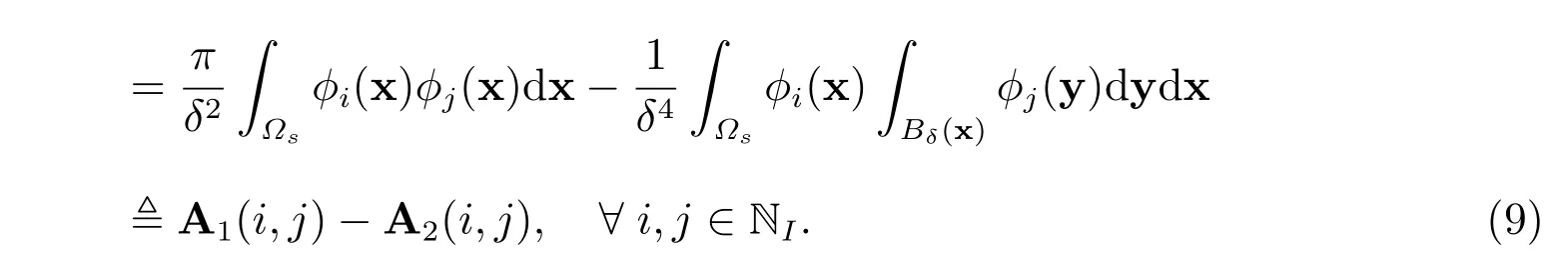
在式(9)中，矩陣A1很容易用通常的方法進(jìn)行計(jì)算，矩陣A2可以計(jì)算如下

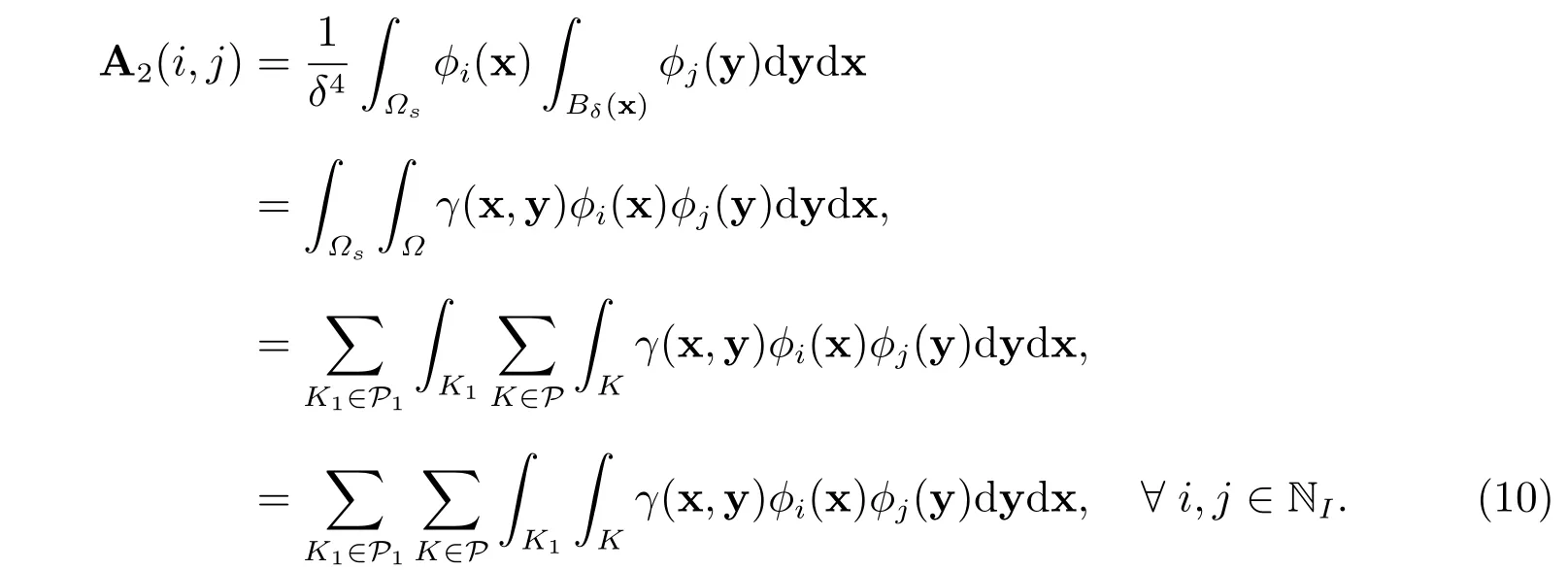
首先，從式(10)取j ∈N 和i ∈NI。然后，可以得到一個(gè)n×n1矩陣

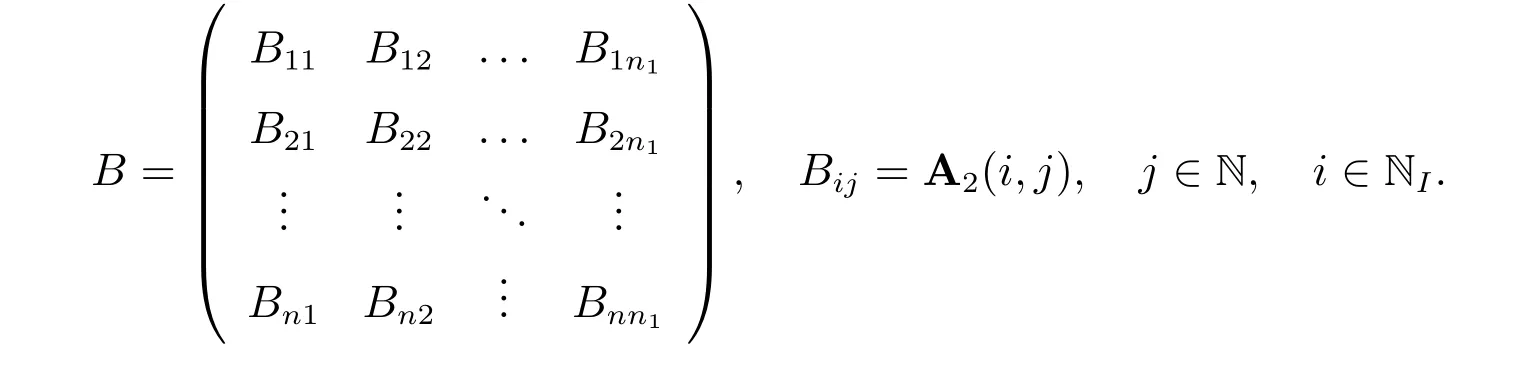
其次，從矩陣B中選取包含?j(y)(j ∈Nb)的元素，矩陣B的其余元素保留并表示為B1，而新矩陣B1恰好就是A2(i,j ∈NI)。據(jù)我們所知，這是第一次用B來(lái)計(jì)算A2。

采用與文獻(xiàn)[18]相似的論證方法，得到如下結(jié)論，此處不再詳細(xì)證明。

定理1如果存在常數(shù)s ∈(0,1)，以及γ?和γ?，使得

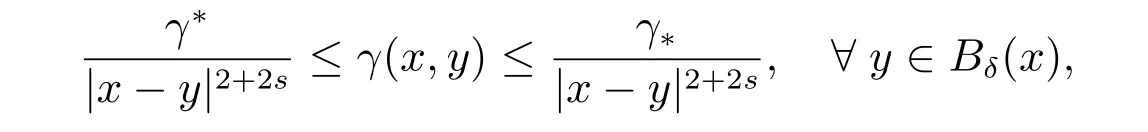
且u ∈V ∩Ht+1(?)，則對(duì)于足夠小的h，存在一個(gè)常數(shù)C，使得

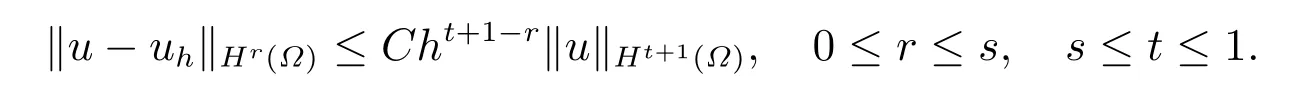
2 數(shù)值算例

我們考慮以下二維非局部擴(kuò)散問(wèn)題

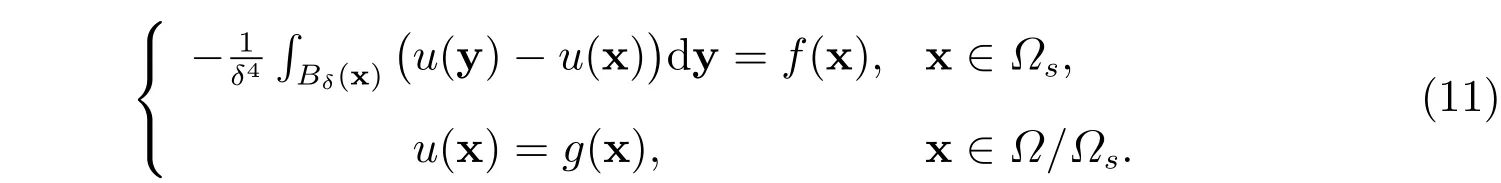
取?s=(0,1)×(0,1),?=(?δ,1+δ)×(?δ,1+δ)，選擇真解為u(x)=x2+y2，則f(x) =和g(x)可以相應(yīng)的計(jì)算得出。表1給出了L2范數(shù)誤差和H1半范數(shù)誤差，其中N為x(或y)方向等分的份數(shù)。

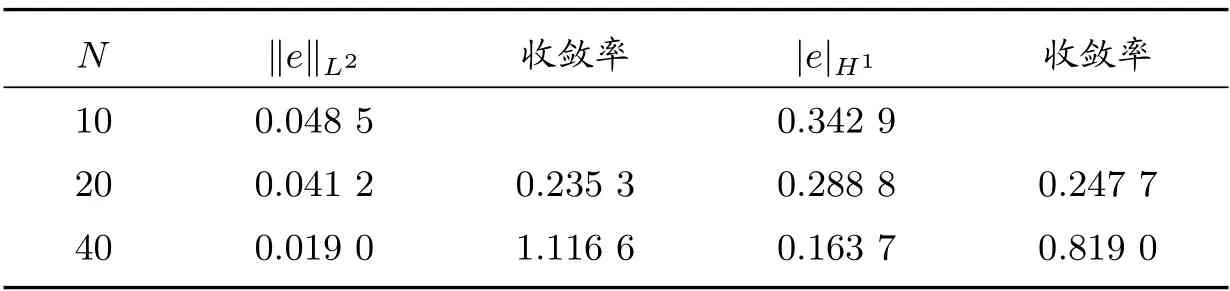
表1 δ =0.2

從表1 中可以看出，當(dāng)網(wǎng)格尺寸H變小時(shí)，對(duì)于分片線性元，L2范數(shù)的誤差收斂階為2，H1范數(shù)的誤差收斂階為1，而文獻(xiàn)[17]中P0元的L2范數(shù)和H1范數(shù)的誤差收斂階都是0.5。因此，可以說(shuō)本文所設(shè)計(jì)的方法的收斂階幾乎是最優(yōu)的。從圖3 中我們看到，當(dāng)網(wǎng)格尺寸h變小時(shí)，數(shù)值解更接近真實(shí)解。

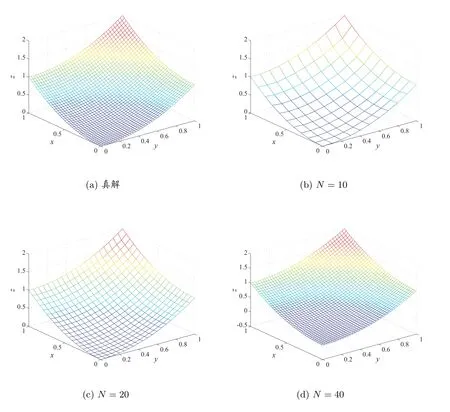
圖3 δ =0.2 時(shí)的精確解和數(shù)值解

3 結(jié)論

本文針對(duì)二維體積約束的非局部擴(kuò)散問(wèn)題提出了一種基于新技巧的高階有限元方法，該數(shù)值方法的剛度矩陣由一個(gè)新的矩陣B提取，該矩陣易于計(jì)算。據(jù)我們所知，用矩陣B來(lái)計(jì)算A2這是第一次，本文給出了元素的編碼原理和數(shù)值計(jì)算節(jié)點(diǎn)的編碼表達(dá)式。同時(shí)，通過(guò)數(shù)值算例，驗(yàn)證了對(duì)于體積約束的非局部擴(kuò)散問(wèn)題中線性有限元方法的誤差L2范數(shù)的收斂速階達(dá)到2，H1半范數(shù)的收斂速階幾乎為1。在今后的工作中，將用本文的數(shù)值方法來(lái)處理Pk(k ≥2)元素。