一類廣義NLS-MKdV 方程族及其雙哈密頓結構

董鳳嬌, 胡貝貝

(1. 滁州學院計算機與信息工程學院，滁州 239000; 2. 滁州學院數(shù)學與金融學院，滁州 239000)

0 引言

在孤子理論中尋找新的可積方程是一個非常重要的研究課題，傳統(tǒng)的方法是使用零曲率方程，李代數(shù)和利用跡恒等式(變分恒等式)，將相應的孤子方程轉化為哈密頓形式[1]。最近，很多新的可積系統(tǒng)利用跡恒等式的經典可積方程的推廣以及其哈密頓形式被構造出來。例如，廣義Ablowitz-Kaup-Newell-Segur(AKNS)孤子族[2]、廣義Kaup-Newell(KN)孤子族[3]、廣義Wadati-Konno-Ichikawa(WKI)孤子族[4]、廣義Dirac 孤子族[5]等。這些廣義孤子系統(tǒng)通常都具有雙哈密頓結構，這保證了遺傳遞歸算子的存在性與Liouville 可積性[6–8]。

帶自相容源的孤子方程在物理學中有著廣泛的應用，它涉及流體力學、固體物理和等離子體物理。一般來說，孤子方程的源會導致孤立波變速運動，使孤子的運動特性發(fā)生了很大的變化。可積系統(tǒng)自相容源描述了不同孤立波之間的相互作用[9–10]。例如，帶自相容源的Kadomtsev-Petviashvili(KP)方程族可以用來描述短波和長波在x–y平面上的相互作用[11]，帶自相容源的Korteweg-de Vries(KdV)方程族可以用來描述等離子體高頻波包與低頻波包權重的相互作用[12]。

經典NLS-MKdV 方程的等譜問題是由Guo 在1997 年提出的[13]。2008 年，Zhang 和Dong 在文獻[14]中給出了經典NLS-MKdV 方程的哈密頓結構。隨后，Chang 和Zhang 在文獻[15]中給出了NLS-MKdV 方程的多分量可積耦合結構。此外，關于二元非線性和分數(shù)階超NLS-MKdV 結構也都被學者研究過[16–19]。本文目的是提出一個廣義的NLSMKdV 孤子族，構造其雙哈密頓結構，并分析其自相容源和守恒律。

本文結構如下：在第1 部分，我們將構造一個基于李代數(shù)sl(2,R)的廣義NLSMKdV 孤子族；在第2 部分，我們利用變分導數(shù)所產生的跡恒等式分析廣義NLSMKdV 孤子族，給出其具有Liouville 可積性的雙哈密頓結構；在第3 部分，我們構造帶自相容源的廣義NLS-MKdV 方程族；在第4 部分，我們借助Riccati 方程研究廣義NLS-MKdV 方程族的無窮守恒律；最后，我們將給出本文的討論和總結。

1 廣義NLS-MKdV 方程族

我們考慮Lie 代數(shù)sl(2,R)的基為

它們滿足如下關系

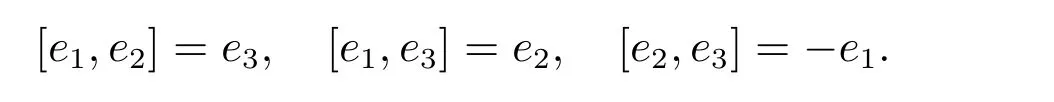
假設Loop Lie 代數(shù)G1的基是{e1(n),e2(n),e3(n)|n ∈Z}，其中x(n)=x?λn。與Lie 代

數(shù)sl(2,R)有關的經典NLS-MKdV 譜問題為

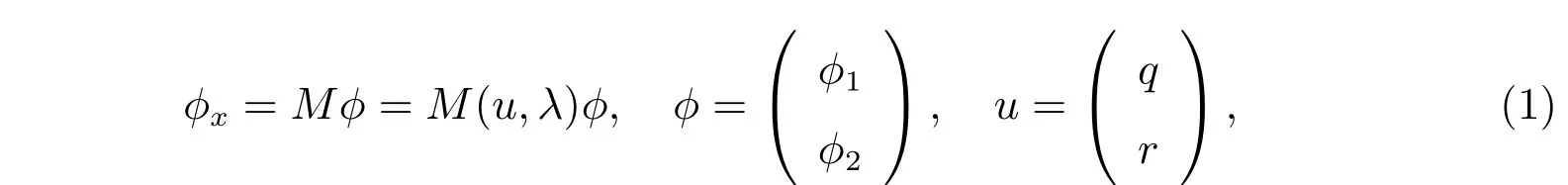
其中

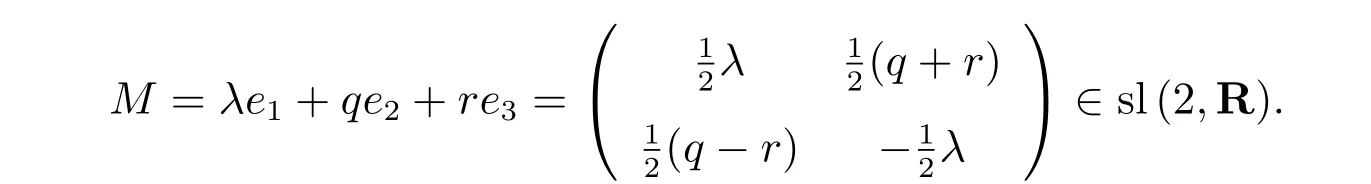
現(xiàn)在，我們引入廣義NLS-MKdV 矩陣譜問題

其中h=μ(q2?r2)，μ是任意的常數(shù)。顯然，當μ= 0 時，矩陣譜(1)就約化為標準的NLS-MKdV 矩陣譜[16]。為了得到與矩陣譜(1)對應的孤子方程族，我們首先解靜態(tài)零曲率方程

其中

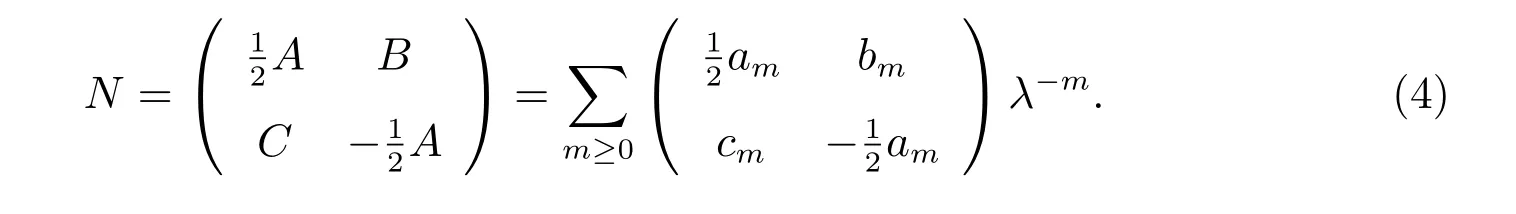
把(2)式定義的M和上述N代入方程(3)，并比較λ同次冪的系數(shù)得到

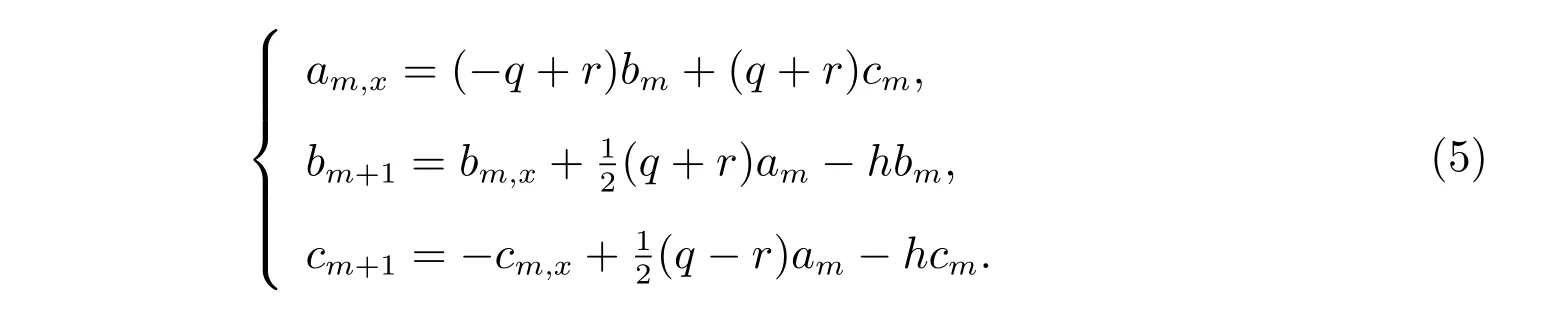
由方程(5)得到遞推公式為

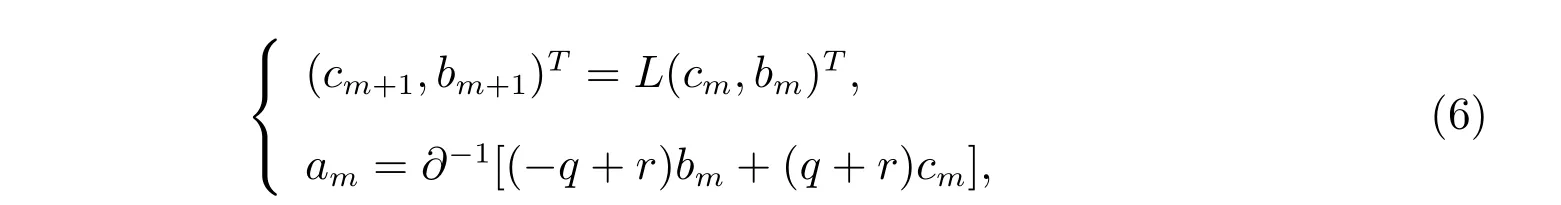
其中??1?=1 且遞推算子L定義為

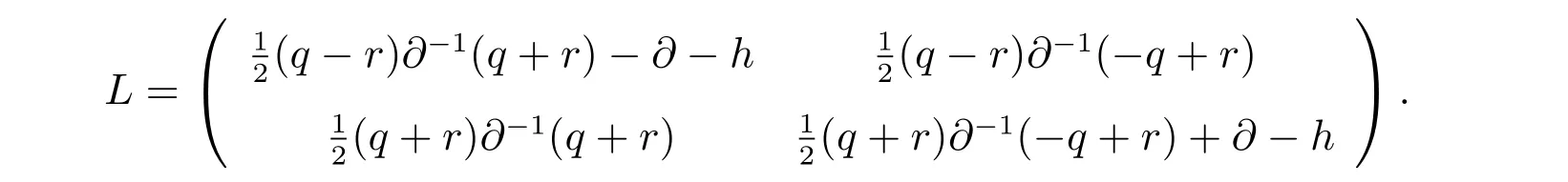
我們選取初始值a0= 1,b0=c0= 0，則aj、bj、cj(j ≥1)可以根據(jù)方程(6)，并借助符號計算軟件Maple 唯一算出，我們列出前三項如下

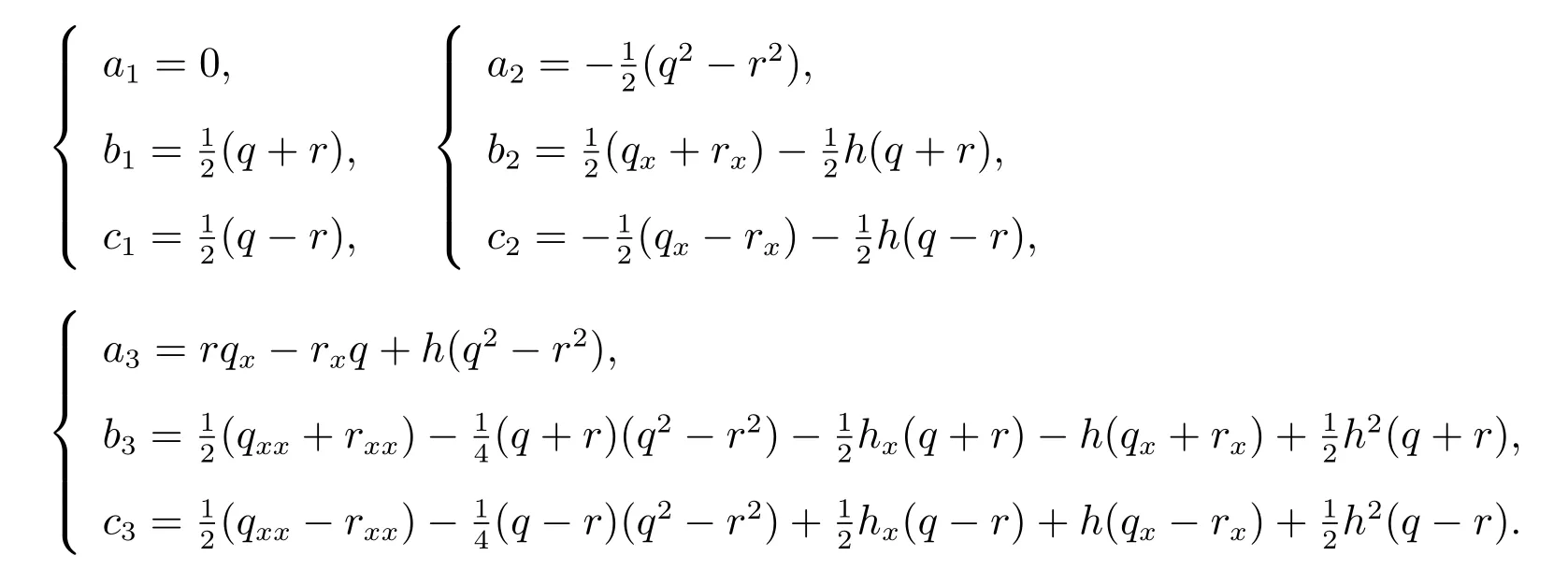
與此同時，我們引入輔助譜?tn=N(n)?，其中

這里?n為修正項，為了不出現(xiàn)標準的NLS-MKdV 情形，我們假設

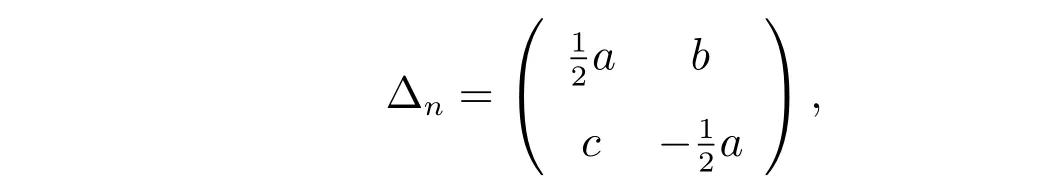
并且把方程(1)和方程(7)代入如下的零曲率方程

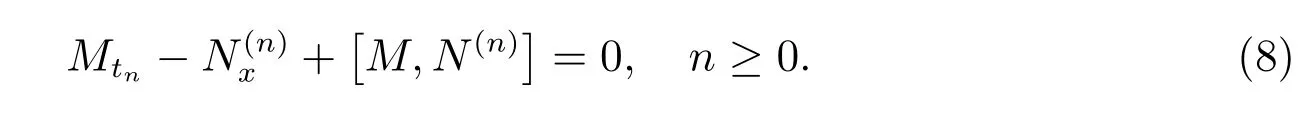
利用方程(5)得到

因此，我們有

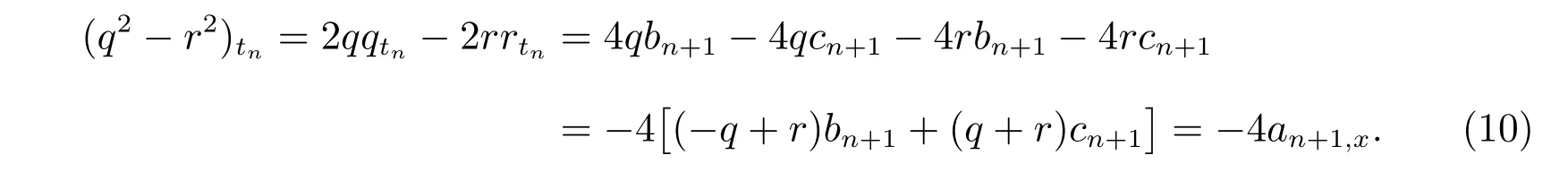
選取a=?4μan+1，我們得到如下的方程族

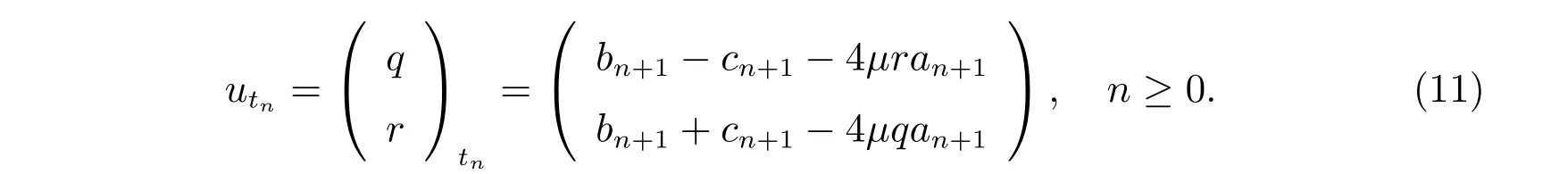
當μ= 0 時，方程(10)就是經典的NLS-MKdV 方程族。因此，方程(11)被稱為廣義NLS-MKdV 方程族。當n=2 時，所對應的方程為

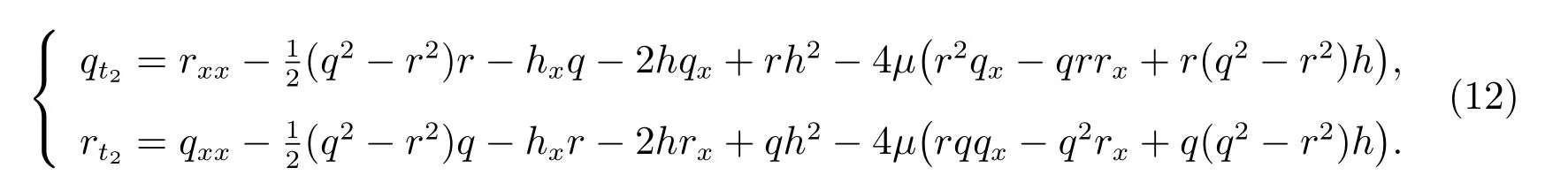
其Lax 對為方程(2)中定義的M和N(2)，而N(2)定義如下

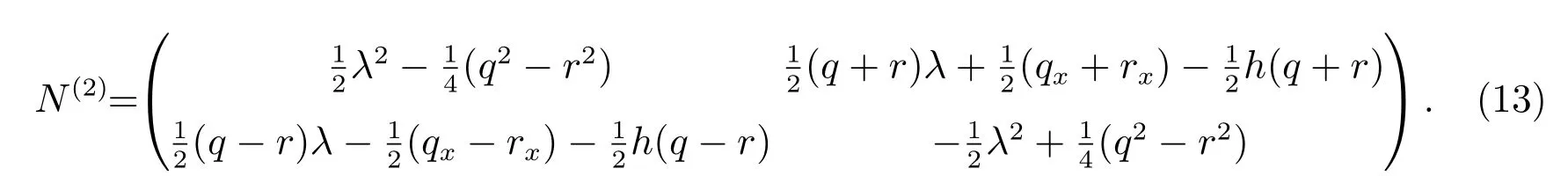
當μ=0 且t2=t時，方程(10)可以約化為經典的NLS-MKdV 方程族[16]

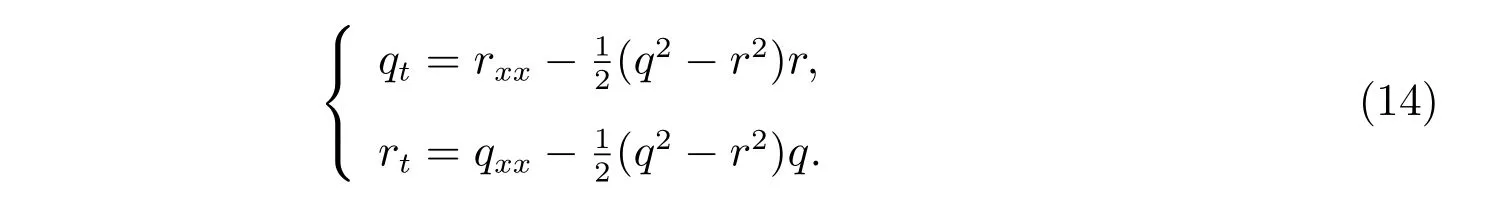
2 雙哈密頓結構

在本節(jié)中，我們通過如下的跡恒等式來考慮廣義NLS-MKdV 方程族的哈密頓結構

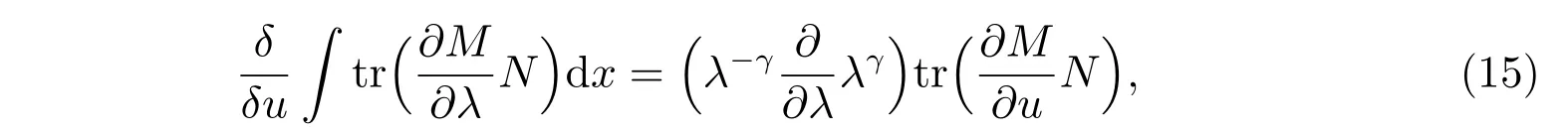
其中

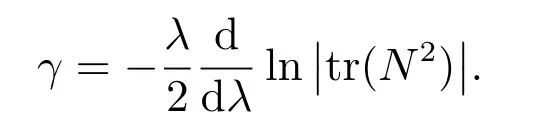
基于上述的跡恒等式，我們有

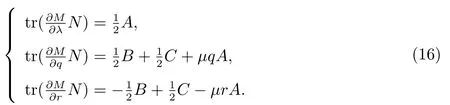
把方程(16)代入方程(15)，比較λ?n?2的系數(shù)，得到

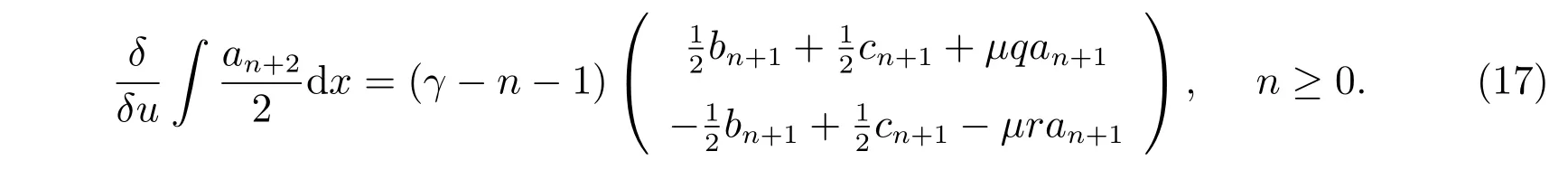
為了確定γ的值，我們令(17)式中的n=0，得到γ=0。因此，我們有

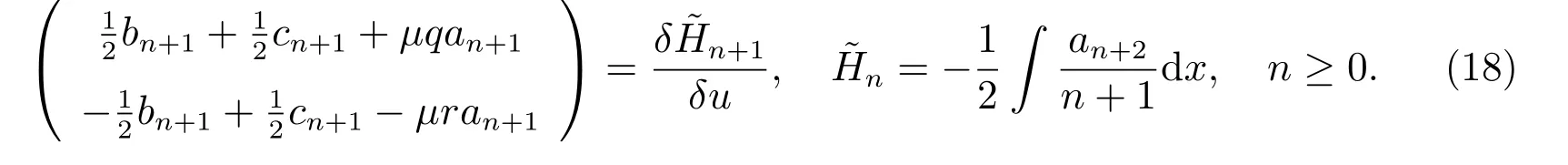
此外，通過直接計算，我們還可以得到

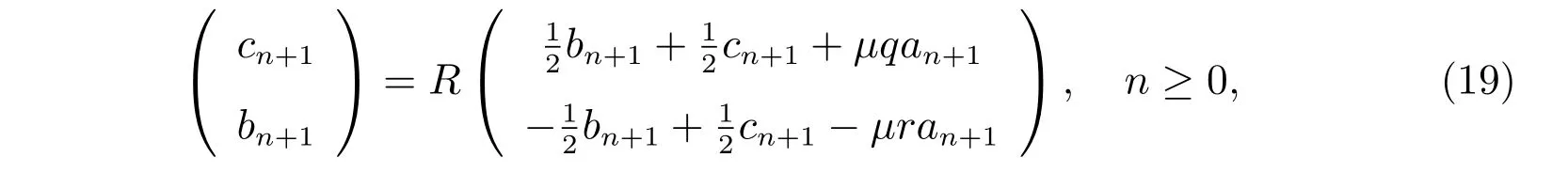
其中R定義如下

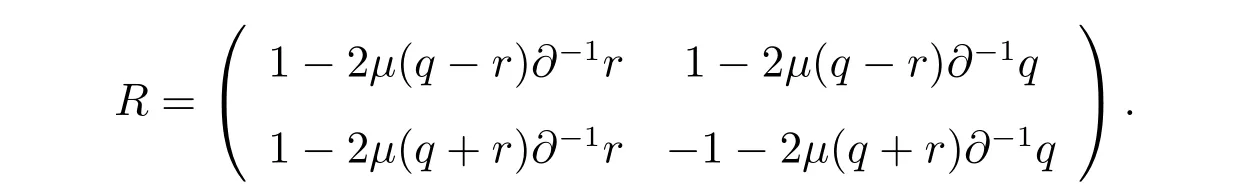
一方面，廣義NLS-MKdV 方程族(10)有如下的哈密頓結構

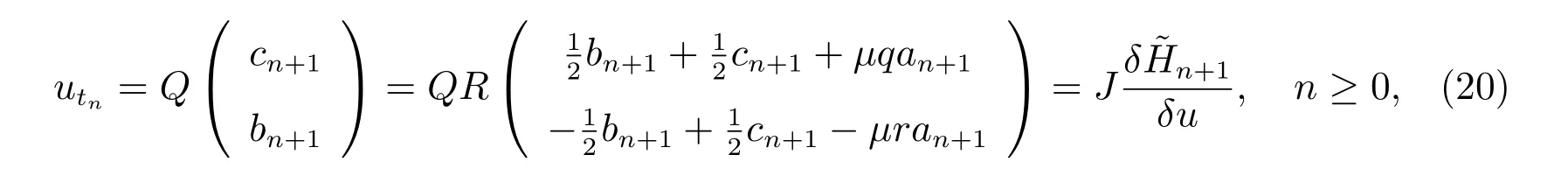
其中

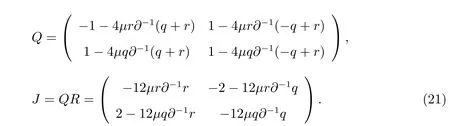
我們可以證明J為哈密頓算子。

另一方面，我們由遞推關系(6)得到廣義NLS-MKdV 方程族有如下的雙哈密頓結構

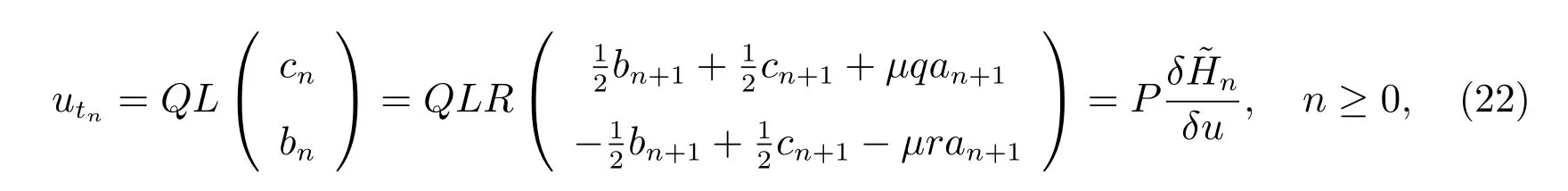
其中P=QLR=(Pij)2×2表示為

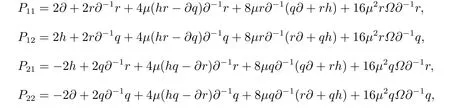
這里?=??1r?r ???1q?q，并且我們可以證明P為第二個相容哈密頓算子。

3 自相容源

這一節(jié)，我們將構造帶自相容源的廣義NLS-MKdV 方程族，在譜問題

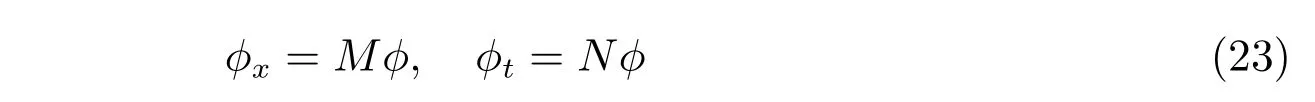
中，令λ=λj，相應的譜向量?記為?j，則得到N個相應的線性問題如下

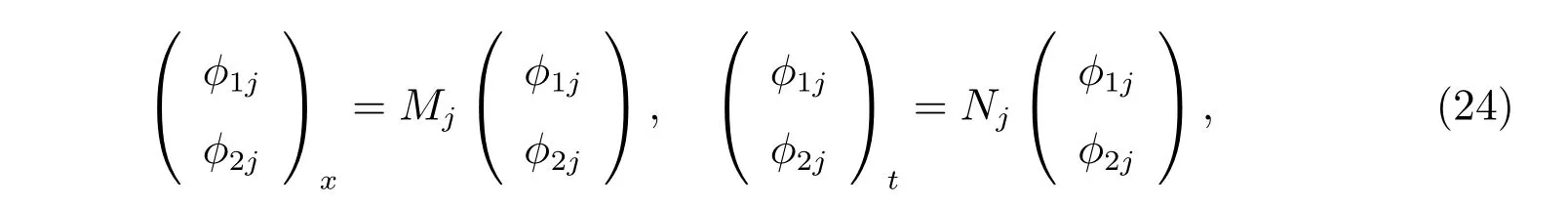
其中Mj=M|λ=λj,Nj=N|λ=λj,j=1,2,···,N。我們還得到

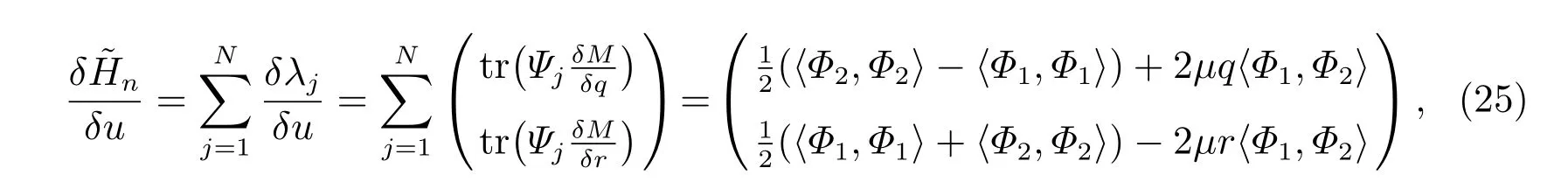
其中Φj=(?j1,?j2,···,?jN)T,j=1,2,3，故帶自相容源的廣義NLS-MKdV 方程族為

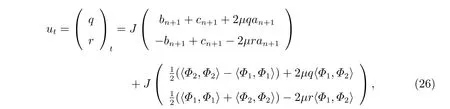
其中J為方程(21)定義的哈密頓算子。

4 守恒律

在這一節(jié)中，我們將要構建廣義NLS-MKdV 方程族的守恒定律。引入變量如下

于是

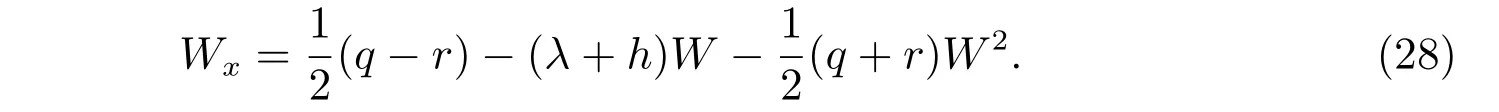
假設

把方程(29)代入方程(28)，并且比較λ同次冪系數(shù)，得到{wn+1}的遞歸公式為

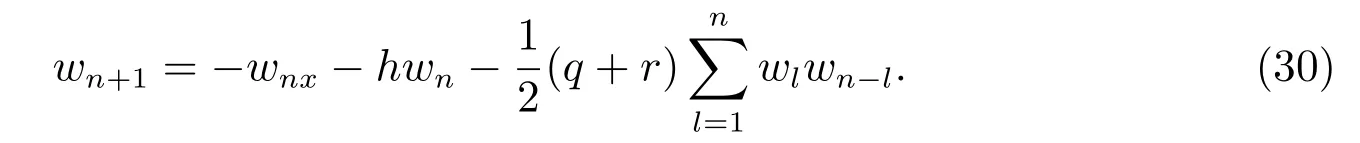
由方程(23)可以得出

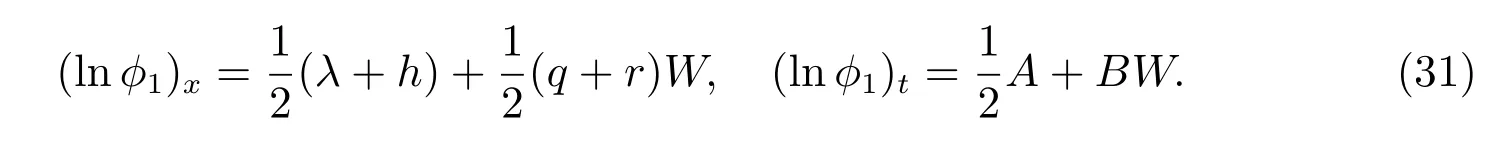
因此，我們有

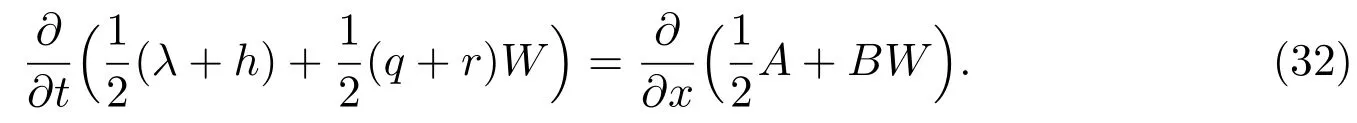
令

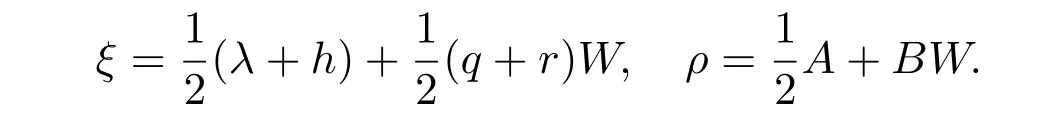
于是，方程(32)等價于ξt=ρx，這正好是n=2 時的守恒定律的標準定義

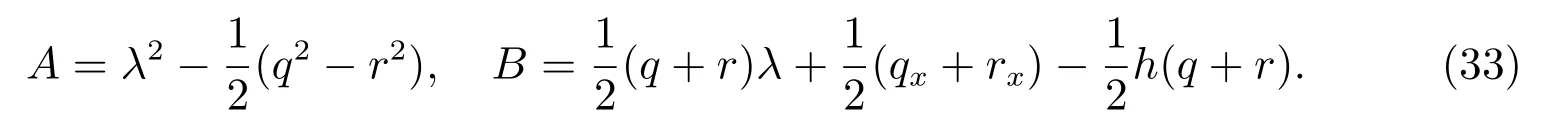
假設

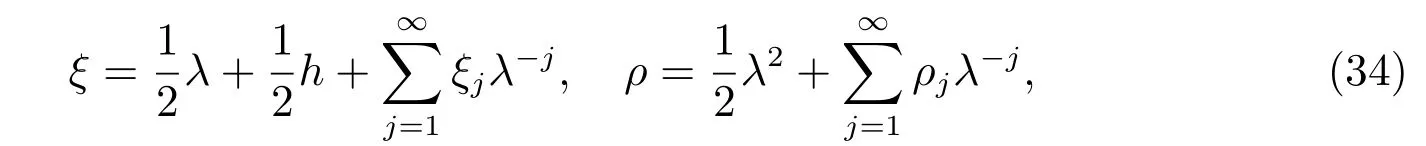
則第一個密度流和守恒量為

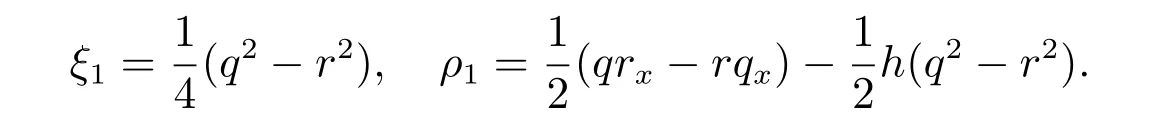
由方程(32)～(34)，得出ξn和ρn的遞歸關系如下

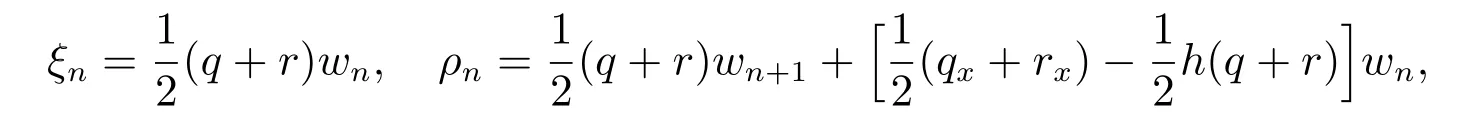
其中wn由方程(30)定義。

5 結束語

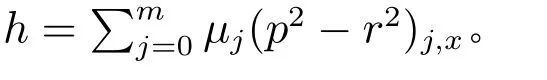
事實上，我們還可以在Lie 代數(shù)so(3,R)上，考慮利用下面的空間矩陣譜問題來構造更一般的廣義NLS-MKdV 孤子族[6–8]

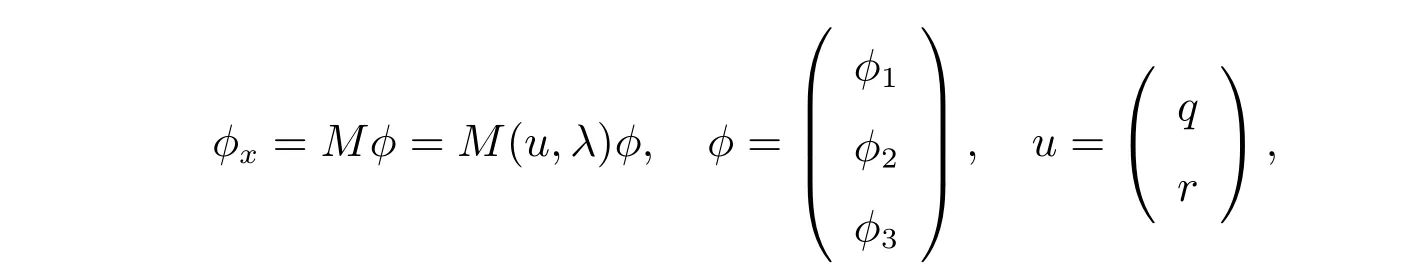
其中

我們還可以將費米子奇變量α和β引入廣義NLS-MKdV 孤子方程族，并將廣義NLS-MKdV 族擴展到超廣義NLS-MKdV 孤子族。其中，費米子奇變量α和β滿足關系為αβ=?βα和α2=β2=0，這些問題將在我們以后的工作中進行討論。