通風高寒隧道凍結鋒面理論計算與工程應用研究

楊 宏

(中鐵二十局集團市政工程有限公司 甘肅蘭州 730030)

1 引言

隨著青藏高原與西北大區域交通基礎設施建設需求持續增加，高海拔寒區隧道工程的建造規模也在逐年擴大[1－2]。其中，降低隧道凍害成為當前亟待解決的關鍵科學問題，也是高寒隧道工程界學者們研究的難點與重點。尤其當洞外處于極端環境溫度，寒冷氣流進入隧道洞內后與襯砌、路面及其下臥的仰拱發生反復熱交換，致使隧道襯砌、仰拱以及排水結構等出現嚴重凍害，這些問題對高寒隧道的運營管理與安全行車造成嚴重困擾[3]。

凍結鋒面作為高寒隧道保溫板設計計算的重要參考，對高寒隧道工程保溫建設具有重要指導價值。然而當前對高寒隧道凍結鋒面的研究成果尚不深入，現有研究主要集中于單管凍結與少部分凍土凍結方面[4－6]，而公路隧道一般半徑較大，且洞內縱向溫度存在差異，斷面溫度差異不可忽略，所以獲取凍結鋒面的解析解較為困難。賴遠明利用攝動技術，得到凍結鋒面半徑與時間控制方程，但未考慮風流場因素及縱向凍結鋒面變化。馮強[7]建立了保溫板條件下寒區隧道凍結鋒面演化控制方程。趙玉報[8]利用FLAC3D技術，研究了凍土隧道圍巖凍結鋒面發展規律。劉鶴[9]依托太錫鐵路太崇段崇禮隧道工程，通過數值計算對季凍性寒區隧道波紋鋼排水溝的適應性進行研究。但目前針對風流場條件下高寒隧道凍結鋒面數學模型計算參數的選取上，未能統一標準。本文依托大阪山隧道，推導出高寒隧道三區域凍結鋒面計算模型近似理論解，與實測數據進行對比分析并修正鋒面參數，理論值與實測值吻合效果良好，可為同類工程提供指導。

2 凍結鋒面控制方程推導與工程應用

2.1 高寒隧道溫度場計算控制方程

本問題涉及相變傳熱，其能量控制方程為:

式中:f、u分別代表凍、融狀態；T、C、λ分別為圍巖溫度、體積比熱與導熱系數。

在移動邊界s(t)上，需滿足連續條件與守恒條件:

式中:Tm為相變溫度；L為含水巖土的相變潛熱；n為移動邊界的方向矢量。

在固定邊界上的邊界條件為:

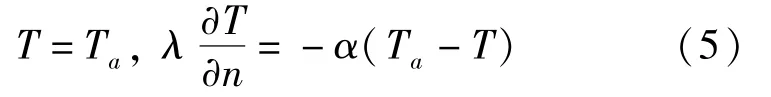
式中:α為巖土熱擴散系數；Ta為環境溫度；n固定邊界的方向向量。

初始條件為:

賴遠明考慮ΔT的影響構造了等價熱容:

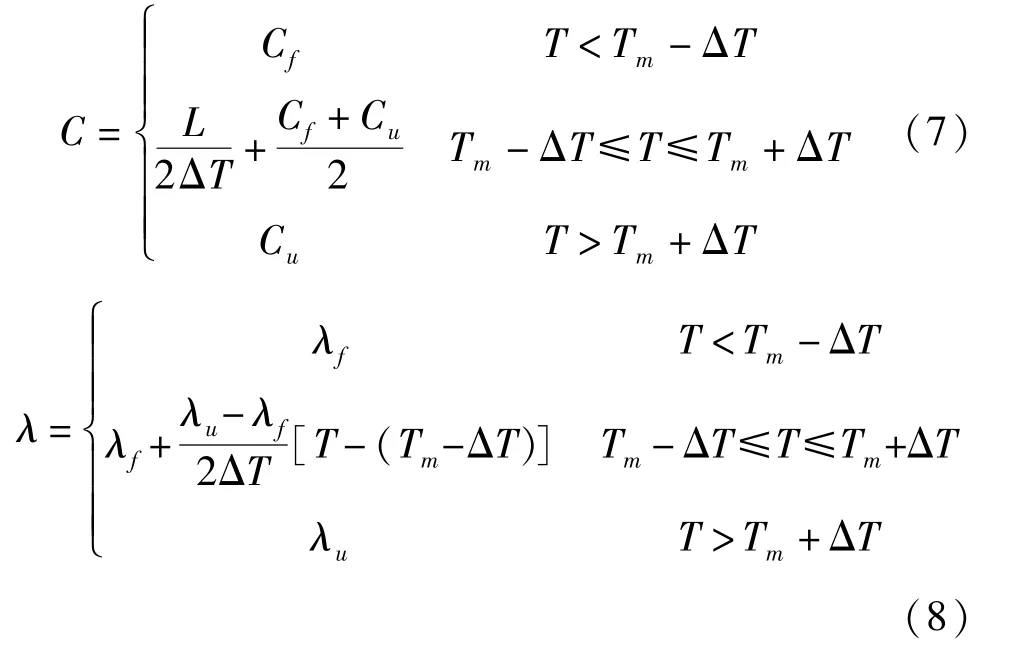
結合式(3)～式(8)，將式(1)～式(2)簡化為:

2.2 高寒隧道溫度場計算相關參數

2.2.1 容積熱容

巖土體容積熱容按下式計算:

式中:C為巖土體容積熱容；Cs為巖土體比熱；ρ為巖土體天然密度。

巖土體比熱按下式計算:

式中:Cus、Cfs、Cdf、Cdu、Cω、Ci分別為未凍土比熱、凍土比熱、凍土骨架比熱、融土骨架比熱、水比熱、冰比熱；us與fs分別代表未凍結與凍結土體；ω與ωu分別為土體含水率與未凍結土體含水率。

2.2.2 導熱系數

各組成物質的導熱系數及相應體積比計算:

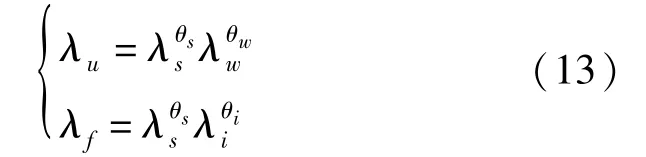
式中:λu、λf、λs、λw、λi分別為未凍土、凍結土、土骨架、水和冰的導熱系數；θs、θw、θi分別為土骨架、水和冰的體積含量。

2.3 潛熱與熵焓理論

常用的潛熱處理方法包括溫度回升法、等價比熱容法和熱焓法，焓定義為:

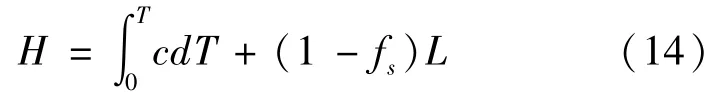
對溫度求導可得:

代入熱傳導方程

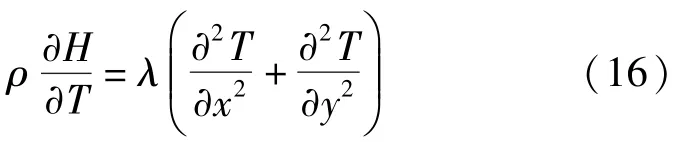
焓值的變化為密度與比熱的乘積對溫度的積分，表示為:

2.4 通風條件下隧道洞內氣溫縱向分布特征計算模型

據統計數據分析可知，隧道洞內縱向氣溫分布規律[10－11]為:

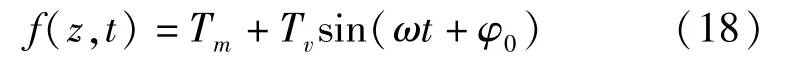
式中:Tm為洞內年平均氣溫；Tv為洞內溫度“振幅”；φ0為相位；ω＝2π/φ，φ為氣溫變化周期。

由于φ0沿隧道縱向變化程度較小，計算時認為φ0為定值，所以只要確定Tm與Tv即可。

圖1為隧道縱向溫度傳熱模型。

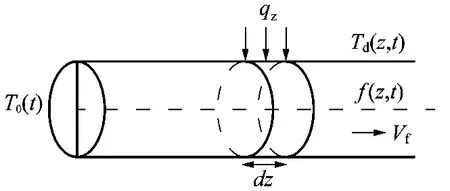
圖1 隧道縱向溫度傳熱模型

圖中:T0(t)為洞口溫度；Td(z，t)為洞壁溫度；f(z，t)為洞內溫度；qz為圍巖與氣體傳遞的熱量；Vf為洞內氣體流速；dz為距離微分單元。

隧道洞內氣體能量守恒方程為:

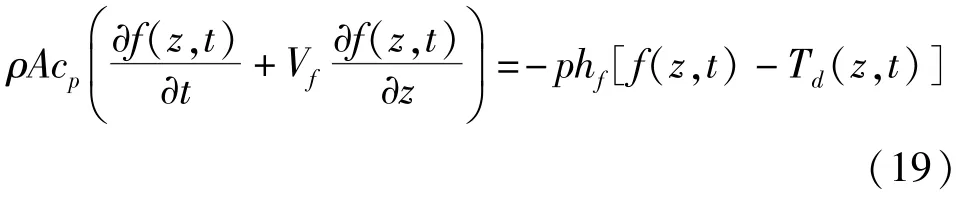
式中:cp為洞內氣體比熱容；ρ洞內氣體密度；A隧道斷面截面積；p隧道環向弧長；hf為圍巖與氣體對流換熱系數。

隧道洞內風速呈冪函數形式衰減，記為Vf＝V(l)，l為隧道進深。

整理可得:

將式(2)和式(4)代入式(5)得:

結合邊界條件Tm＝Tm0，z＝0得:

將式(2)和式(4)代入式(5)還可得到:

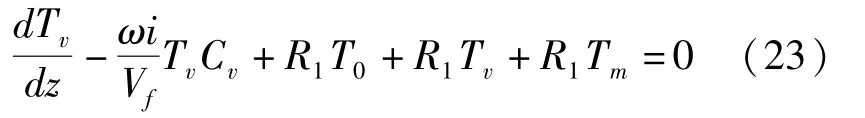
式中:R1為隧址區凍結埋深[9]。

結合邊界條件Tv＝Tv0，z＝0得到:

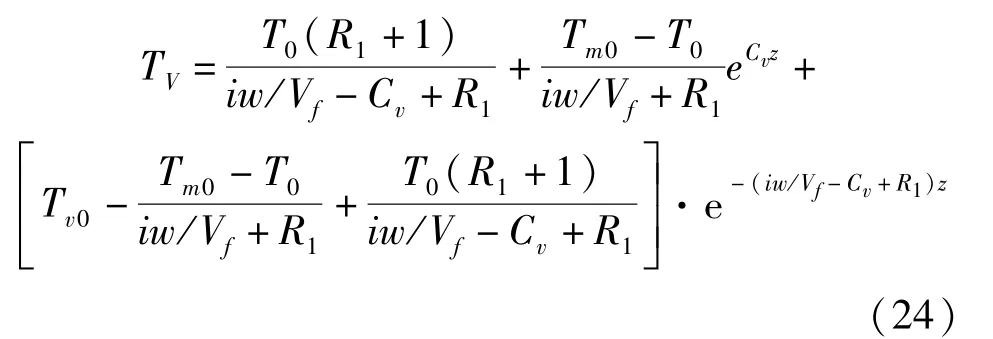
式中:T0為洞口溫度；d為隧道等效半徑；dl為隧道圍巖溫度場影響半徑；p為隧道環向弧長；ks為圍巖導熱系數；α為巖石熱擴散系數。

進而得到高寒隧道縱向溫度場分布規律:

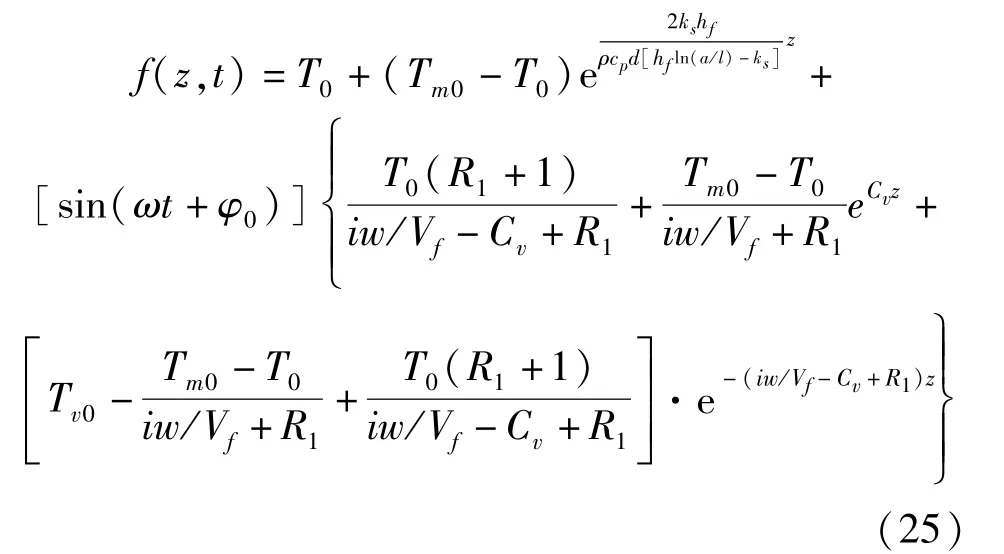
2.5 通風條件下高寒隧道凍結鋒面計算模型

凍結區域溫度為Tf，未凍結區域溫度為Tu，凍結鋒面半徑為R(t)，凍結鋒面處的溫度Tj＝0℃，隧道半徑為Rt，隧道洞內熱流密度為q。圖2為凍結鋒面示意圖。

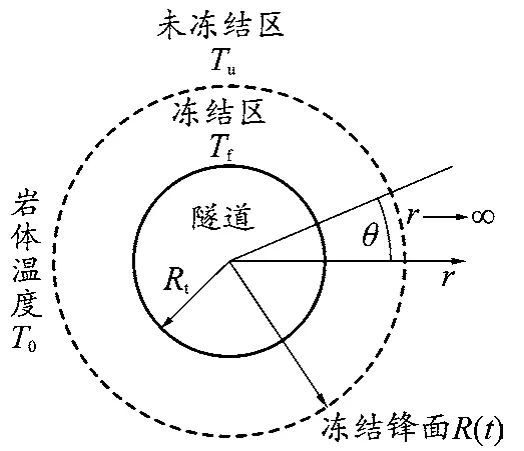
圖2 凍結鋒面示意

其熱傳導微分方程為:

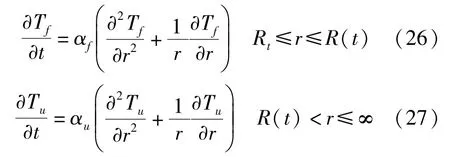
式中:αf、αu為熱擴散系數，且有:

式中:λ、c與ρ分別為導熱系數、比熱與飽和密度。

熱傳導微分方程的初始條件為:當t＝0時，Tf＝Tu＝T0。

熱傳導微分方程邊界條件為:

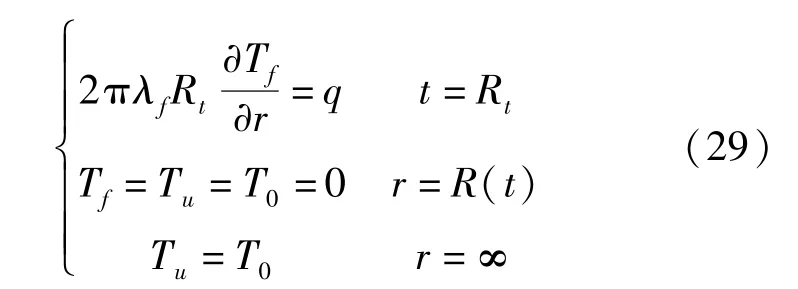
按照集中參數法[12]，其熱流量表達式為:

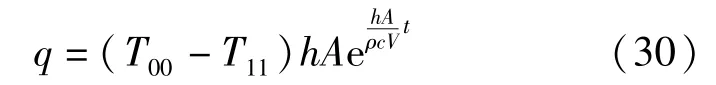
式中:h為固體與流體的表面傳熱系數；A為物體表面積；V為物體體積；c為比熱；ρ為密度；T00為初始溫度，置于隧道洞內氣溫為T11的流體中，即:

在相變界面R(t)處的熱方程為:

式中:L為單位容積巖體相變潛熱，即:

式中:Lw為單位質量水的相變潛熱；ρd為巖體的干密度；w0為巖體的初始含水率；wu為巖體中未凍結水含量。

對導熱微分方程進行求解，得到溫度場分布規律:

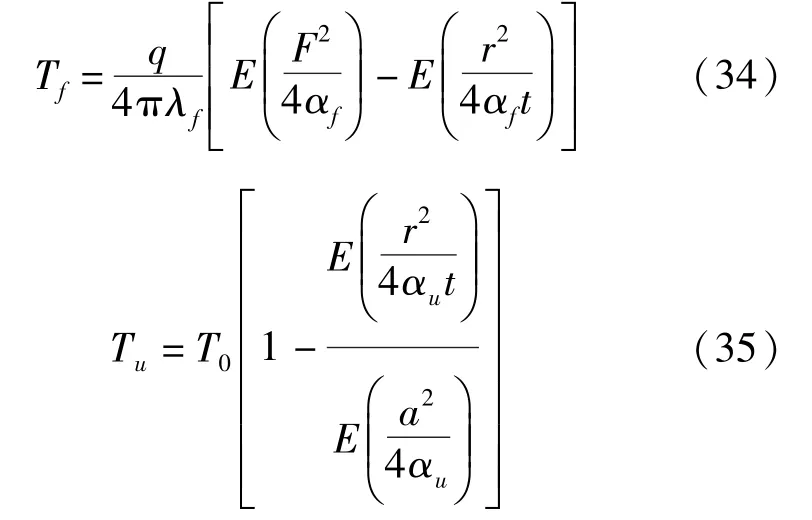
將式(2)與式(17)代入式(20)得:

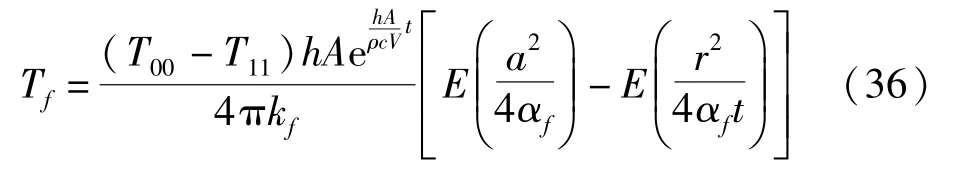
將式(9)與式(7)相應的Tm與Tv代入式(22)可得到凍結區域溫度場分布規律。

式中:E為指數積分函數，滿足:

當r＝R(t)時，Tf＝Tu＝0，基于單管凍結理論及平板凍結理論，結合有關研究成果，鑒于隧道斷面溫度不同，將理論凍結鋒面劃分為三個區域，每個區域的斷面初始溫度不同，結合彭立敏[13]研究成果及蔣斌松[14]研究成果，得到凍結鋒面半徑與時間的平方根關系方程:

式中:t為時間，d；a、b、c為待定系數。

風流場條件下高寒隧道溫度場可由單管凍結理論近似求解，當確定巖土體的熱物理參數后，凍結鋒面半徑可采用式(38)進行計算。

2.6 凍結鋒面理論解工程實例對比分析

以某高寒隧道實測溫度數據為依據，對凍結鋒面理論解與實測值進行對比分析，驗證理論解的合理性。

取空氣與圍巖對流換熱系數hf＝h＝12.0W/(m2˙K)，巖體的熱擴散系數為αf＝0.114 m2/d、αu＝0.225 m2/d，凍結區圍巖比熱與導熱系數分別為cf＝1.617×103J(kg˙K)、λf＝1.824 W/(m˙K)，未凍結區圍巖比熱與導熱系數分別為cf＝1.929×103J(kg˙K)、λf＝1.434 W/(m˙K)，體積相變潛熱為ρL＝46.44 ×106J˙m－3，圍巖初始溫度為1.5℃，密度為ρ＝2.5×103kg/m3。

根據物理模型試驗結果[15]，圖3為凍結鋒面區域劃分。由于實測數據只有區域二、三現場實測凍結深度，結合模型試驗結果來獲得區域一凍結深度現場數據。基于現場區域二、三凍結深度，通過建立模型試驗三個區域凍結深度的關系可以得到區域一凍結深度數據，具體方法為:

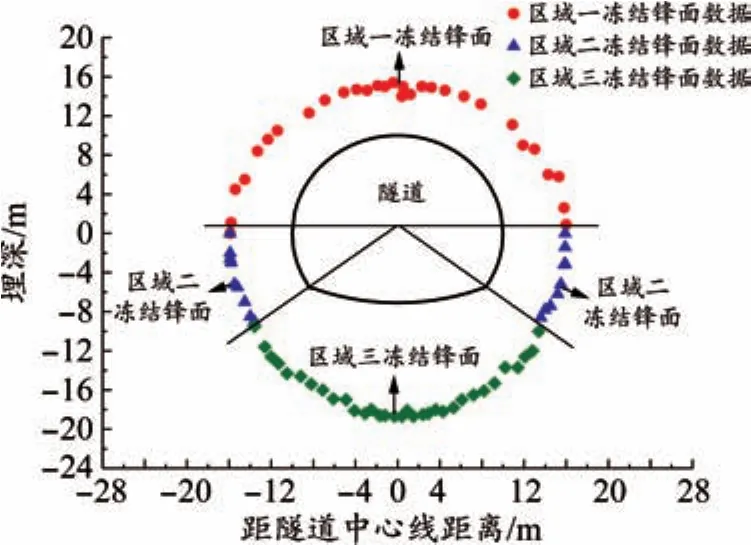
圖3 凍結鋒面區域劃分

將模型隧道凍結鋒面區域一、二、三分別簡化為平均凍深，三個區域平均凍結深度存在關系:

區域一平均凍深∶區域二平均凍深∶區域三平均凍深 ＝1∶1.17∶2.36。

通過對現場區域二與區域三凍結深度關系對比(區域三平均凍深/區域二平均凍深)，可以看出每個時期的凍結深度關系波動范圍在1.85～2之間，與模型試驗區域二與區域三平均凍深2.07較為接近，說明模型隧道三個區域凍結深度關系與現場三個區域實測凍結深度關系類似。

取隧道進深z＝20 m，由于現場測試數據有限，只有10～12月及次年1～3月數據，通過6個月的實測數據進行理論計算，結果與現場實測結果進行對比分析。將所有參數代入式(38)，三個區域待定系數b分別為0.15、0.18、033，表1～表3為理論解與實測值。

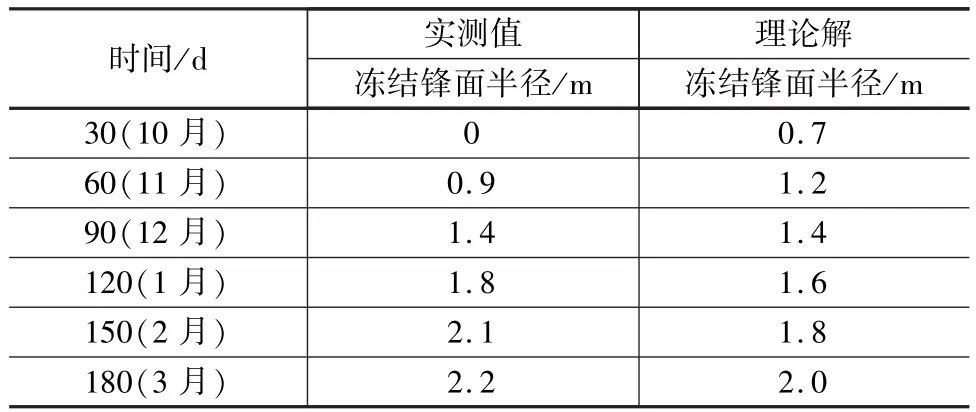
表1 凍結鋒面計算值與實測值比較(區域一)

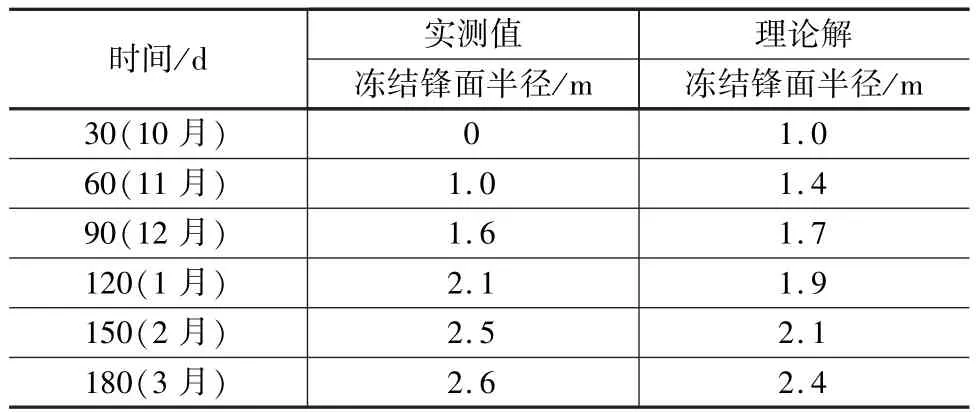
表2 凍結鋒面計算值與實測值比較(區域二)

表3 凍結鋒面計算值與實測值比較(區域三)

得到凍結鋒面方程為:

將實測值與理論值進行相關性分析，見圖4～圖6。以區域二為例，當t<100 d，理論解與實測值相關性較低；當t>100 d，理論解與實測值接近程度增加，但計算值與實測值的相關系數屬于低度相關，建議采用修正系數對理論解進行修正分析。

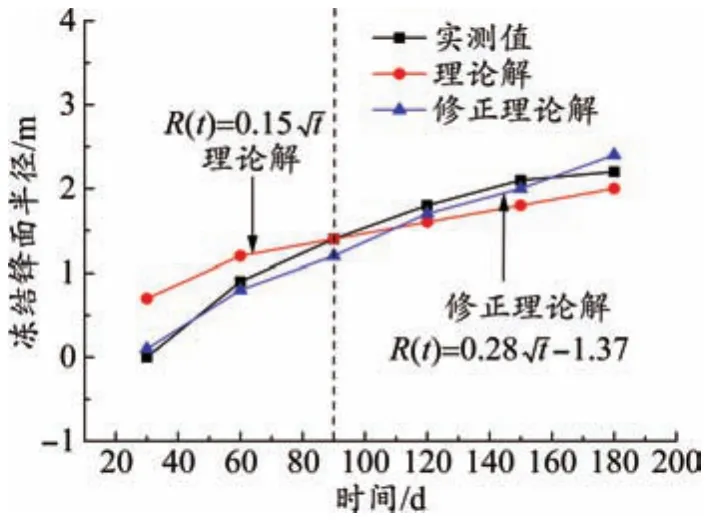
圖4 凍結鋒面區域一理論解與實測值對比

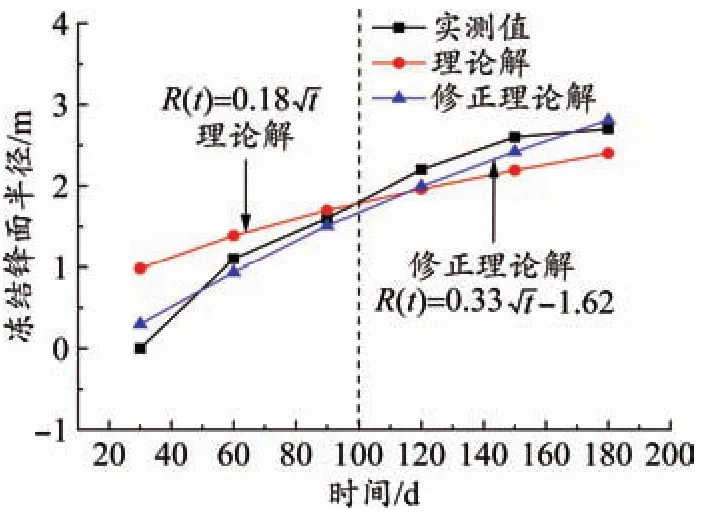
圖5 凍結鋒面區域二理論解與實測值對比

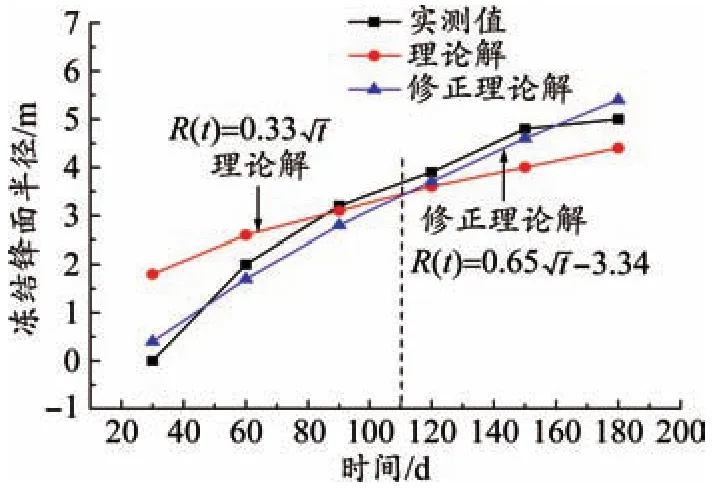
圖6 凍結鋒面區域三理論解與實測值對比

修正原理采用相關系數最大化法，采用不同函數形式擬合現場數據，函數類型應與推導的理論方程相同，通過SPSS軟件進行不同擬合函數與現場數據的相關系數分析，得到相關系數最大擬合控制方程，然后再比較相關系數最大擬合控制方程與理論方程差異性，得到修正系數。

修正凍結鋒面方程為:

式中:m、n為修正系數。

經計算，區域一修正系數m、n分別為1.87、－1.37，區域二修正系數m、n分別為1.83、－1.62，區域三修正系數m、n分別為1.97、－3.34，基于Perason相關系數計算法，修正理論計算值與實測值的相關性達到最大，結果較為可靠，見表4～表6。

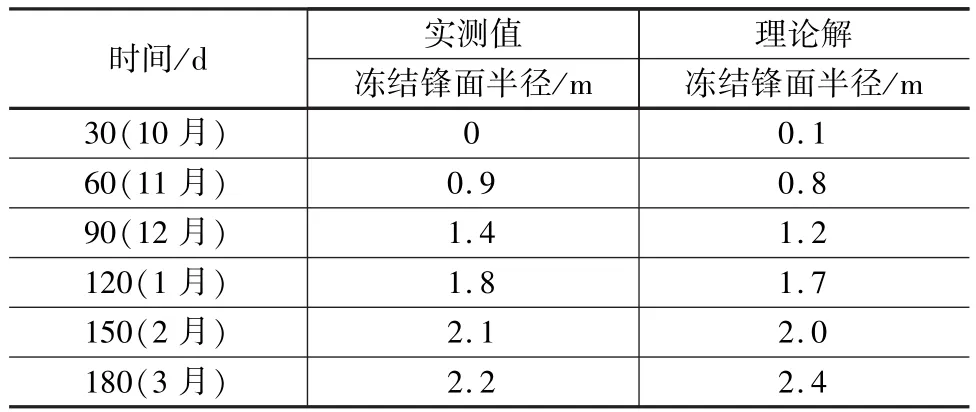
表4 修正凍結鋒面計算值與實測值比較(區域一)

表5 修正凍結鋒面計算值與實測值比較(區域二)

表6 修正凍結鋒面計算值與實測值比較(區域三)

可見，凍結鋒面修正理論解能夠反映實測鋒面分布特征，通過確定隧道進深，可以得到整個風流場條件下高寒隧道不同進深處的凍結區域具體分布特征。

3 結束語

(1)基于風流場條件下的高寒隧道縱向氣溫計算模型，考慮單管凍結理論與瞬態熱傳導物體熱流量，給出了通風條件下高寒隧道凍結鋒面理論計算模型。

(2)對比分析了高寒隧道凍結鋒面理論計算值與實測值，并對凍結鋒面理論解進行修正，修正后的三個區域凍結鋒面可以用于現場高寒隧道的近似估算以及溫度場數值模擬的準確性檢驗。