小學數學教材研讀之面積教學的思考與研究

徐錦萍

(銅陵市田家炳小學 安徽銅陵 244000)

“認識面積”作為一節被專家們研究透了的課，以新想法去建構，會有新的突破嗎？實踐能給出最好的證明。

一、深度解讀教材，理清知識體系

數學課程標準中提出數學概念和數學思想應該是層層遞進、逐級深入的。數學教材也體現了這個理念。但是在實際教學中，很多教師卻對教材知識體系的掌握不太重視。在學習“面積”知識點之前，學生已經初步認識了各種平面圖形，了解了長方形和正方形的邊、角的特征，以及長方形和正方形的周長計算方法，而充分理解“面積”的概念可以為后面學習面積單位和探索平面圖形面積的計算方法打下重要的基礎。因此，學習好這節基礎課有著非常重要的作用。

二、豐富面積概念，善用動手操作

筆者認為在學生對“面積”有了一定的認識的前提下，從圖形入手，更有利于教學。波利亞指出：“學習最有效的方法就是自己去探索發現。”學生學習的過程中如果能夠發揮他們的自主性，自己去探索，發現問題，那在這樣的學習過程中收獲的經驗和知識是最能夠內化成他們自己的東西的。

“面積”概念對于學生來說是比較抽象的，所以學生在學習中要動手體驗，這就需要教師給予學生充分動手的機會。怎樣實現更有效的課堂操作活動呢？筆者認為應該注意以下三點：以學生為中心，喚醒他們自身的活動經驗；充分做好教學準備，在學生充分理解的前提下實現教學目標；提高學生數學學習的能力，為后面的學習做好鋪墊，積累豐富的活動操作經驗。

我們可以嘗試這樣設計：

【片段】平面圖形的大小就是它的面積

師：這是一個長方形，請你用彩色的粉筆表示出它的面積。

一位學生用筆畫出這個長方形一周的邊。

生1：他描的是長方形一周的長度，這是周長，不是面積。

生2：把長方形的面涂出來(同學們基本都同意這樣來表示這個長方形的面積)。

師：你們為什么不同意前面那位同學的表示方式呢？

生3：他描的是長方形的總長，是周長，不是面的大小。

師：畫的是邊框，表示的周長而不是面積。

師：像黑板面和數學書的封面就可以用觀察法比較面積大小。現在有一個正方形和一個長方形，它們的面積相差不大，現在還能直接觀察出誰面積大，誰面積小嗎？(如圖1)

圖1

生4：長方形面積大、正方形面積小。

生5：用尺子量一量。

生4：用尺子不能直接量出圖形的面積，只能知道周長。

生5：可以用尺子測量出這個長方形的長要比這個正方形的邊長要長，長方形的寬和正方形的邊長相等，所以長方形的面積大。

師：老師明白了，你仍然是通過測量邊的長來推算圖形面積，這也是一個很好的計算方法，但這不是這節課學習的內容，后面的課程中我們會重點研究的。

生4：把這兩個圖形重疊起來。正方形的邊長等于長方形的寬，通過測量邊的大小可以比較出它們的面積大小。

師：用一個小長方形(出示)就可以比較黑板上兩個圖形的面積大小。(正方形剛好是三個小長方形那么大，長方形比三個小長方形還大些。)

師：除了老師的小圖形，你們可以自己選擇小圖形嗎？除了小長方形，還可以用小正方形嗎？(可以)如果選擇小正方形作為測量標準，測量兩個大圖形的面積，就相當于把這兩個大圖形分別擺方格紙上，比較它們分別占的小正方形的個數。(出示透明方格紙，學生數方格。)

三、數形結合，深化理解

(一)數形結合，區分周長和面積

經過以上的學習，學生對面積已經有了一定的認識。學生空間觀念薄弱，他們對更為抽象的“面積與形狀”和“面積與周長”不是很容易就能區分開。所以在教學過程中教師需要采用更為直接的方法來幫助他們理解，如數形結合。

1．數一數。(如圖2)

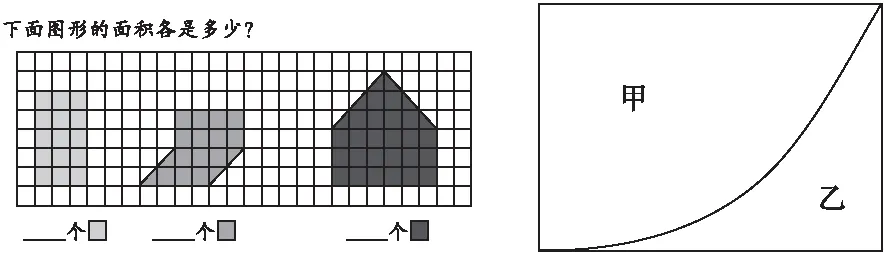
圖2 圖3

2．判一判。(如圖3)

(1)甲部分的面積比乙部分的面積大。

( )

(2)有兩個圖形，如果它們的面積相等，它們的形狀也一定相同。

( )

3．畫一畫：請在格子圖中畫出一個與左邊圖形面積相等而形狀不同的圖形。(如圖4)

圖4 圖5

4．辨一辨：周長與面積的區別。(如圖5)

比較這些面積都是4的圖形，它們的周長相等嗎？

小結：當兩個圖形面積相等時，它們的周長不一定相等，形狀也不一定相同。

以上練習關系緊密。特別是最后兩題，學生最容易做錯。這樣的練習有利于學生將面積與“形狀”“周長”有效聯系，靈活轉化，滲透了數形結合的思想，也讓學生的空間觀念得到進一步發展。

(二)數形結合，理解面積的概念

數形結合就是把抽象的事物具體形象化，把復雜的數量關系用幾何圖形表示，既直觀又簡潔。用圖形來幫助理解數量關系，這樣更有利于理解題意，優化解題方法。

對于空間圖形的概念的理解，筆者認為數形結合是最適合學生的方法。就像本節課中提到的“圖形的面積相等，周長未必相等”，如果只是給學生講道理、說事實，沒有與圖形相結合，學生很難真正理解和掌握。

例如：面積是12平方厘米的平行四邊形，想象一下它的底和高分別是多少？請在格子紙上畫出來。(如圖6)學生通過動手操作發現，等底等高的平行四邊形，其面積相等，理解了“面積相等的平行四邊形不一定就是等底等高平行四邊形”的道理。

圖6

數學結合的思想方法把復雜的問題變得簡單化，讓抽象的問題有了形作為依托。學生能一目了然，不需要老師過多地講解也能理解，而且理解得比較透徹，達到了此處無聲勝有聲的效果。

四、深度解讀教材，有效建構概念

(一)研讀教材，明確目標

數學課程標準中明確闡述了小學數學教學的本質。數學的教學其實是一個個數學活動，是教師和學生們相互交流、共同發展的過程。而教材是課堂教學中非常重要的一個因素。教師應在正確理解教材、使用教材的基礎上，指導學生采用有效的學習方式，培養學生的數學素養。本節課應在具體的事物和圖形中建立面積的表象，并以此理解面積的其他屬性。

但是如果對教材產生錯誤理解，就會使教學偏離方向。比如在執教三年級上冊《倍的認識》時，某教師誤認為本課的教學目標是“認識倍的含義”和“求一個數的幾倍”。新課結束后，他發現很多學生不能準確理解“倍”的含義。而本課的教學目標本來應該是讓學生在模仿、操作、感悟中理解“倍”的含義。我們在教學中只要把倍的概念講透，其他的就會水到渠成。

(二)有效操作，拓寬思維

蘇霍姆林斯基說過：“人的手和大腦之間有著不可分割的聯系,動手操作能夠使大腦得到發展,能讓它更聰明；大腦能夠使手更靈活,能讓它成為思維的工具和鏡子。”這告訴我們，數學教學過程中動手操作的重要性。教師在教學過程中必須要重視學生的內在能動性，促使學生積極探索。在這個過程中，我們需要提供充足的時間和空間給學生動手實踐，不能流于形式，否則就達不到真正的教學目的。比如“面積”教學中，比較兩個圖形的大小時，教師運用了豐富的材料，其中有53個三角形、30個正方形、15個圓等。如此多的材料對學生思維的沖擊是巨大的，實踐證明效果明顯。

這樣的空間圖形教學案例還有很多。比如“四邊形的認識”教學中，在判斷“凹四邊形”是不是四邊形時，學生之間出現了爭議。教師在教學時引導學生“變一變”。

2．師：有的說是，有的說不是。請大家仔細看，現在老師拉動其中的一個頂點，它還是四邊形嗎？為什么？(有學生回答只要這個圖形有4條直直的邊、4個角就是四邊形)

師：說得不錯，我繼續來拉動(如圖7)，請用手勢判斷。(四邊形→長方形→凹四邊形)

3．小結：不管四邊形的形狀怎么樣，只要這個圖形有4條直直的邊、4個角，它就是四邊形。

4．師：我們繼續來變動這個圖形，看看它還是不是四邊形？為什么？(三角形)現在它是四邊形嗎？為什么？(學生回答不是，因為只有3個角、3條邊。)

圖7

通過這樣的圖形變形，學生清楚地了解了四邊形的概念，明白不管形狀是怎樣的，只要有4條直直的邊、4個角，它就是四邊形，突破了教學難點。這樣的操作實踐活動可以為學生的學習積累非常寶貴的感性材料，同時建立了非常豐富的表象，加深了學生對知識的理解。因此在平時的課堂中，教師一定要重視學生的動手操作，激發學生學習的內在動力，以達到學生充分理解知識點的目的。

五、結語

總的來說，教材是我們進行教學的根本，離開教材談教學，相當于無源之水。我們不斷地“深入”教材，才能讓學生的學習更有深度。與此同時，我們也需要關注學生掌握知識點的現狀，運用多種方法幫助學生認識和理解概念，更要關注學生實際操作的過程，構建更有效的數學課堂，提高教學效率，從而培養學生的數學素養。