具有動態領導者的多智能體系統分組一致性控制
胡順偉,陳向勇, 邱建龍,趙 峰
(臨沂大學自動化與電氣工程學院,山東臨沂 276005)
0 引言
一致性控制是多智能體系統協同控制的關鍵問題。一致性控制旨在利用智能體自身和相鄰智能體的狀態信息設計控制器,實現群體狀態的趨同。當前,一致性思想已在微電網均衡調壓、無人機協同,以及編隊控制中得到了廣泛的應用,因此備受關注,相關的成果也接連涌現。
文獻[6-7]研究了一類線性多智能體系統,通過設計動態事件觸發協議,在不需要全局信息的情況下實現了無領導者的一致性控制。文獻[8]則通過狀態分解的方法,實現了可以隱藏初始狀態信息的平均一致性控制。文獻[9]通過在觸發間隔引入估計器,減少了相鄰觸發間隔的狀態偏移,實現了有領導者的跟蹤一致性控制。相較于無領導者一致性和初值平均一致性,有領導者的跟隨一致性問題復雜度更高,更具有挑戰性。文獻[10]研究了在切換拓撲下有領導者的線性多智能體系統,利用系統在觸發時刻的狀態設計了控制器,實現了不依賴于全局信息的領導-跟隨一致性控制。文獻[11]設計了一個虛擬領導者,利用非周期間歇通信機制,解決了帶時滯非線性多智能體系統的領導-跟隨問題。文獻[12]分別設計了集中式和分布式的控制器,在兩種情況下分別實現了領導-跟隨漸近一致性控制。在上述文獻研究中,領導者的動力學模型不存在控制輸入且模型相對保守。目前,對領導者存在控制輸入的動力學模型的研究還相對較少,具有一定的研究意義和研究前景。
此外,隨著工業生產要求的提高,智能體往往要求完成多目標任務,智能體之間的信息交互不再是簡單的合作關系,而是伴隨著合作-競爭的信息交互。在合作-競爭信息交互下,具有合作信息交互的智能體的狀態趨于相同值,具有競爭信息交互的智能體的狀態趨于相反值。這種情況下,傳統的群體一致性控制器變得不再適用,需要一些新的分組協議來實現這種控制目標。文獻[13]通過引入預設時間函數,在事件觸發機制下實現了一階多智能體系統的分組一致性控制。文獻[14]討論了合作、強競爭、弱競爭三種交互關系,設計了一種切換控制律,實現了異構二階多智能體系統分組一致。文獻[15]設計了一個非光滑控制器,利用自適應控制消除了對全局信息的依賴,解決了線性多智能體系統的領導-跟隨一致性問題。然而,這些研究所提出的方法只適用于具有一階、二階或線性動力學模型的多智能體系統,而實際中多智能體系統模型大多是非線性的。
需要指出的是,一些領導-跟隨一致性控制問題中所研究的領導者模型是不具有控制輸入的,此類模型保守性較大,適用范圍較小。理論上,這種模型可以看作領導者的控制輸入為零時的一類特殊情況。其次,相關文獻往往僅考慮了單一合作或競爭的信息交互,對于合作-競爭交互給系統帶來的影響并沒有進一步的研究和說明。事實上,合作-競爭交互共存時給系統帶來的影響是顯著的,它不僅體現在實現一致性行為軌跡上的不同,而且在網絡拓撲結構上也發生了明顯的變化,一些群體一致性拓撲結構性質也變得不再適用。此外,非線性問題一直是系統控制的難點和重點,在考慮動態領導者和合作-競爭機制后,實現非線性多智能體系統一致性更具困難和挑戰。
基于上述分析,本文主要研究了在合作-競爭交互下具有動態領導者的非線性多智能體系統的分組一致性控制問題。主要貢獻如下:
1)相較于文獻[10]和文獻[12]中不具有控制輸入的領導者動力學模型,本文考慮了具有非零控制輸入的領導者,并且領導者的輸入對每個跟隨者都是未知的。傳統的零輸入領導者可看作是本文的一種特殊情況。
2)本文考慮了合作-競爭交互機制,相較于文獻[16-18]中單一合作或競爭交互,本文研究的問題復雜度更高。
3)利用分組機制設計的控制器,適用范圍更加廣泛,本文設計的控制器不僅適用于合作-競爭交互的智能體系統,對于單一合作或競爭交互的多智能體系統也適用。
1 預備知識
1.1 圖論
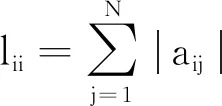
1.2 問題描述
考慮如下由1個領導者和個跟隨者組成的非線性多智能體系統
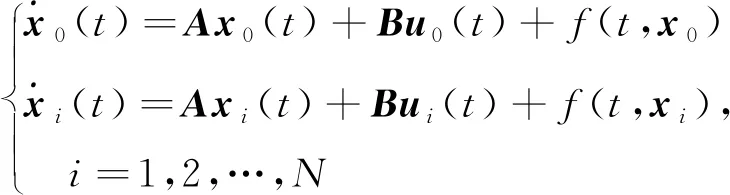
(1)
其中,∈和∈分別代表領導者智能體的狀態和控制輸入。∈,∈分別代表跟隨者智能體的狀態和控制輸入。:×→是在時間上連續可微的已知的非線性函數。、是具有適當維數的常數矩陣。
在文獻[8]和文獻[9]中,領導者不帶有控制輸入,這可以看作是系統(1)在()=0時的一種特殊情況。而本文中研究的領導者具有控制輸入且與跟隨者的相對狀態無關,其相對于跟隨者是未知的。
與系統(1)相關的符號圖是結構平衡的,并且包含一個由領導者作為根節點的有向生成樹。如果領導者是智能體的鄰居,則0=1,否則0=0。
若符號圖是結構平衡的,則存在一個符號矩陣=diag(,,…,),使得矩陣所有項都是非負的。其中,當節點處于同組時=1,當節點處于不同組時=-1。
(,)是可穩的。

非線性函數滿足下列不等式
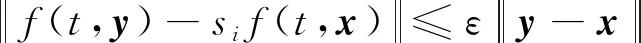
(2)
其中,>0是一個常數。
假設1是實現分組一致性控制的一般假設條件,在此條件下滿足圖拉普拉斯矩陣的一些特殊性質。假設2是保證Riccati不等式可解的條件。假設3中()是一致有界的,這在實際控制中是可行的。假設4是一類Lipschitz-like條件,用于解決分組一致性控制中非線性函數帶來的困難。
當如下條件(3)被滿足時,系統(1)可實現領導-跟隨分組一致性控制。
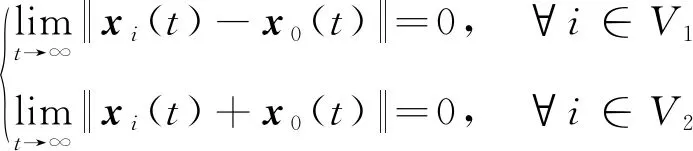
(3)
跟隨者智能體和領導者之間的狀態誤差定義為
()=()-()
(4)
由引理1和上述等式可知,本文主要解決的問題是在合作-競爭交互的多智能體系統(1)中設計分組控制器和,使得
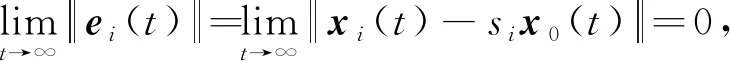
(5)
成立,從而實現系統(1)的領導-跟隨分組一致性控制。
2 主要結果
首先,對誤差系統(4)求導可得
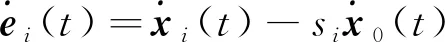
=()+()+(,)-
(()+()+(,))
(6)
為了在符號圖中實現系統(1)的分組跟隨一致性控制,設計如下的控制器
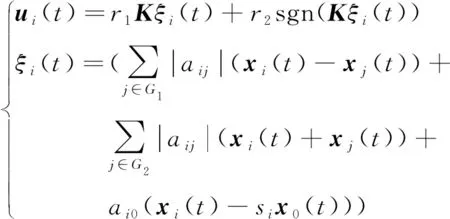
(7)
其中,,>0,是在下文中被設計的參數;∈表示智能體與智能體屬于同一組,∈表示智能體與智能體屬于不同組;表示領導者與跟隨者是否同組,同組=1,不同組=-1。
合作-競爭交互在控制器(6)中體現為同組智能體之間為合作關系,其狀態最終趨于相同值;不同組智能體之間為競爭關系,其狀態最終趨于相反值。本文考慮的是二分組情況,智能體的鄰居智能體只屬于或,且∈∪,這種分組機制相較于文獻[17]和文獻[20]中群體一致性更具有應用前景。
結合上述所設計的控制器(7),式(6)可改寫為如下緊湊形式

(?)sgn((?)())-
(?)()+()
(8)
其中,=+,=diag(,,…,0)表示領導者與跟隨者的通信關系,表示由個跟隨者智能體組成的通信拓撲圖的拉普拉斯矩陣,
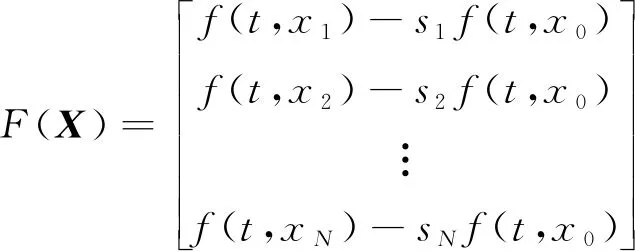
(9)
之后,對誤差進行如下變換
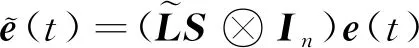
(10)
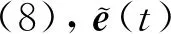
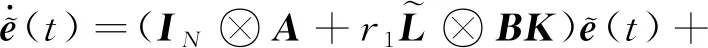
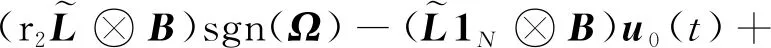
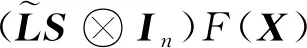
(11)
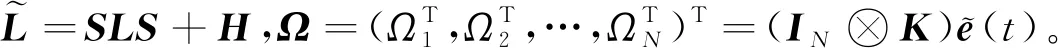
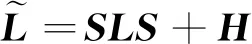
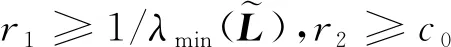
+-2++<0
(12)
選擇Lyapunov函數為
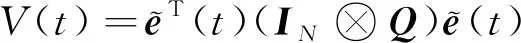
(13)
對式(13)求導可得
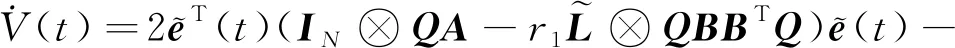
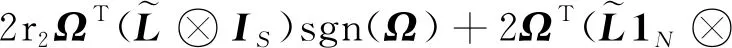
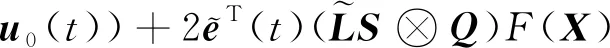
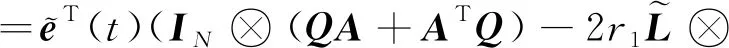
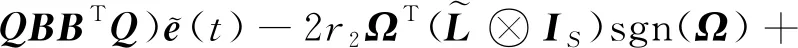
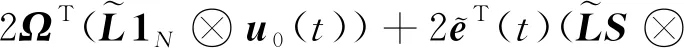
)()
(14)
結合假設4,式(15)成立
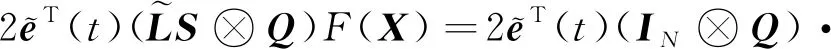
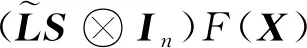
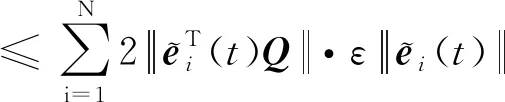
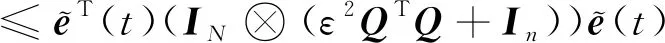
(15)
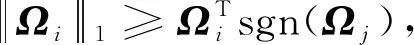
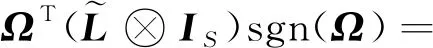
(?)sgn()+(?)sgn()
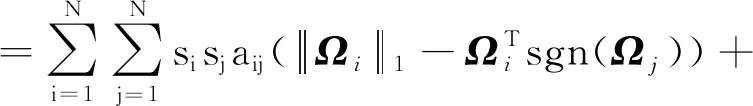
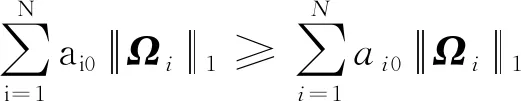
(16)
根據假設3可知
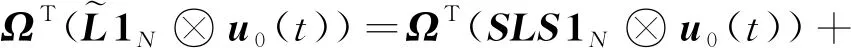
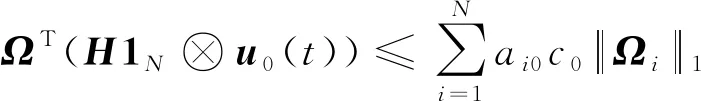
(17)
成立,因此,式(14)可寫為
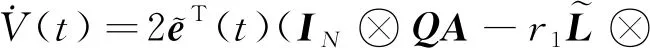
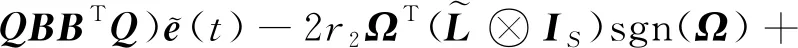
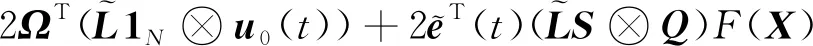
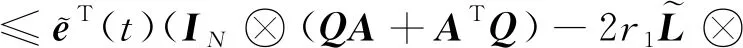
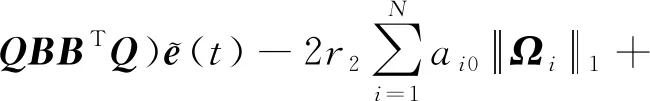
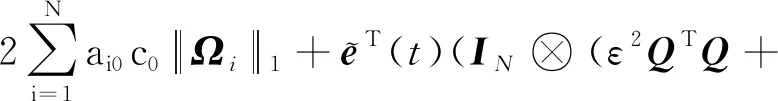
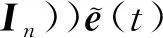
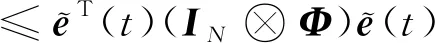
(18)
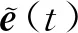
控制器(7)可以進一步轉化為(19),控制器(19)可以有效地消除抖振現象。
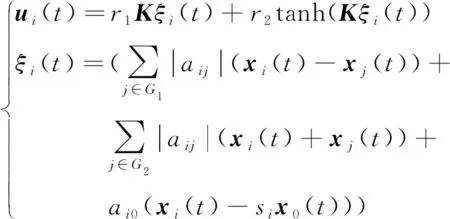
(19)
3 數值仿真
考慮由1個領導者和5個跟隨者構成的多智能體系統,如圖1所示,其中,領導者0和智能體1,2,3為同組;智能體4和5為同組。
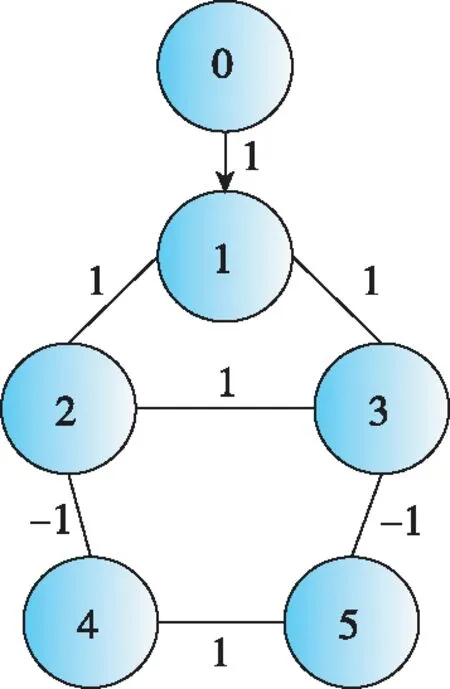
圖1 通信拓撲圖Fig.1 Communication topology
由圖1可以計算出
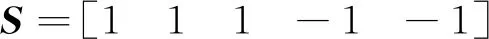
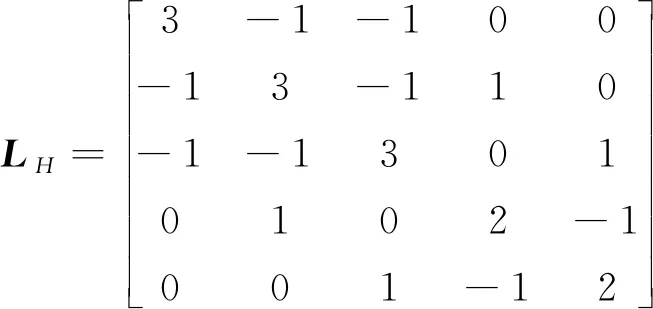

選擇系統的參數如下
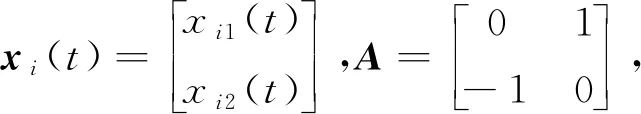

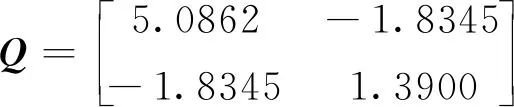
可得
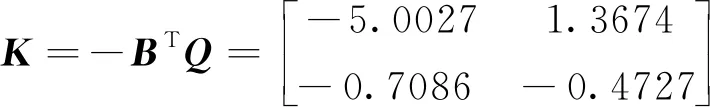
設定系統初始狀態值為
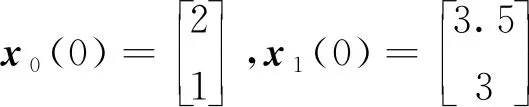
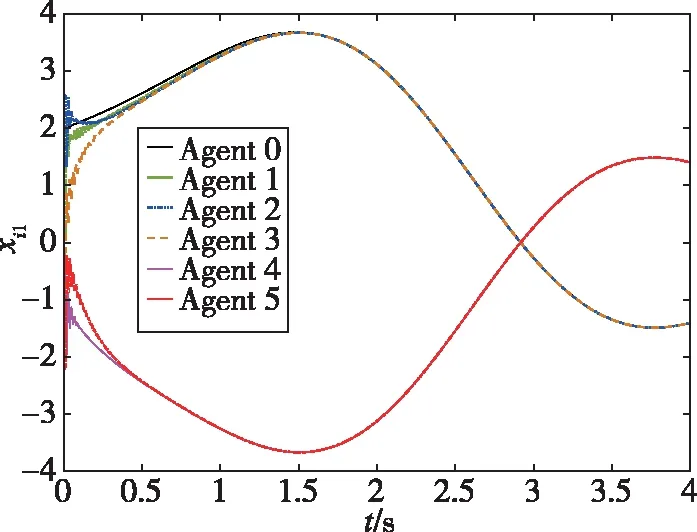
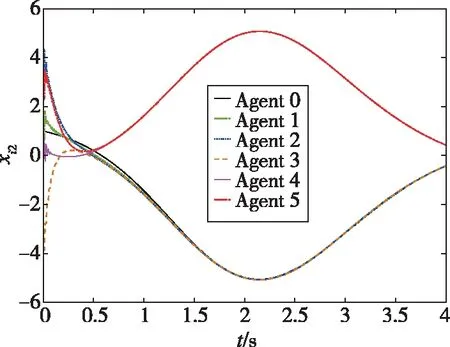
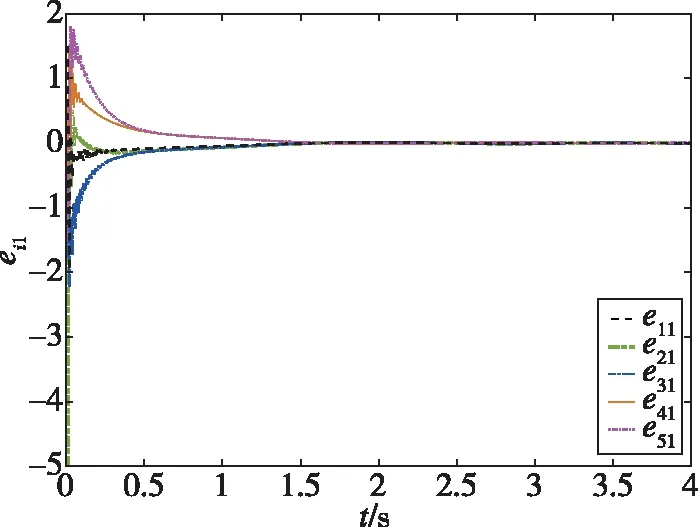
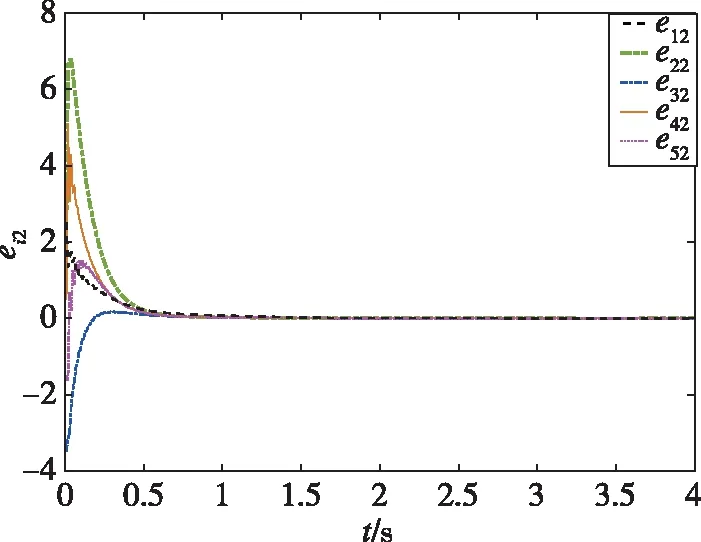
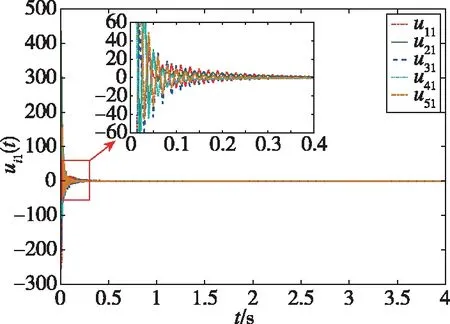
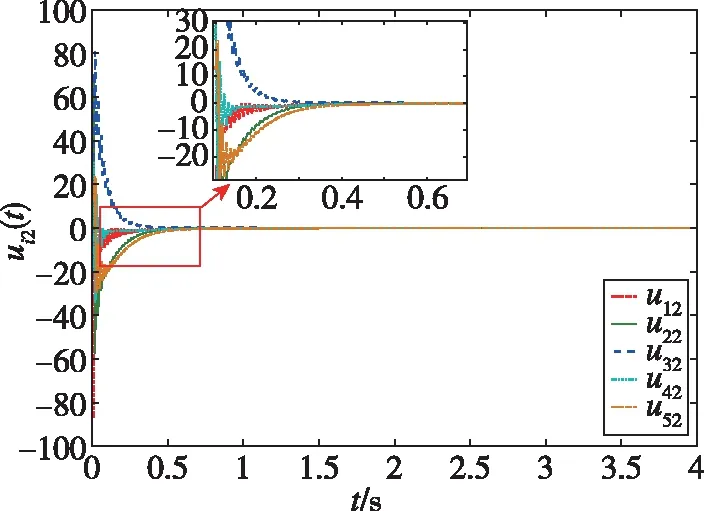
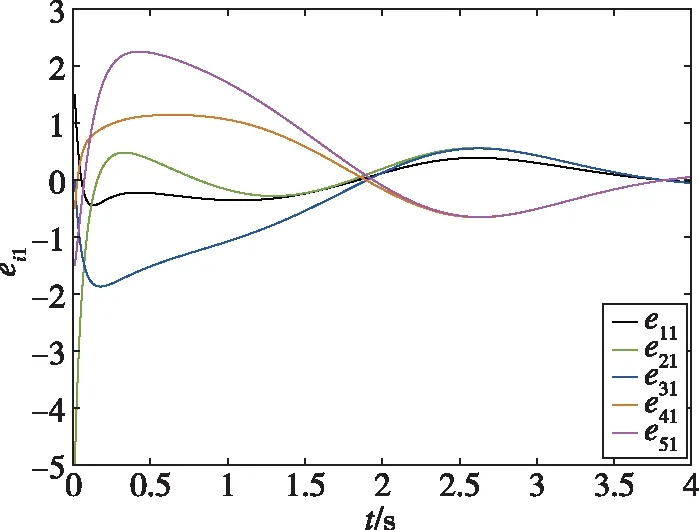
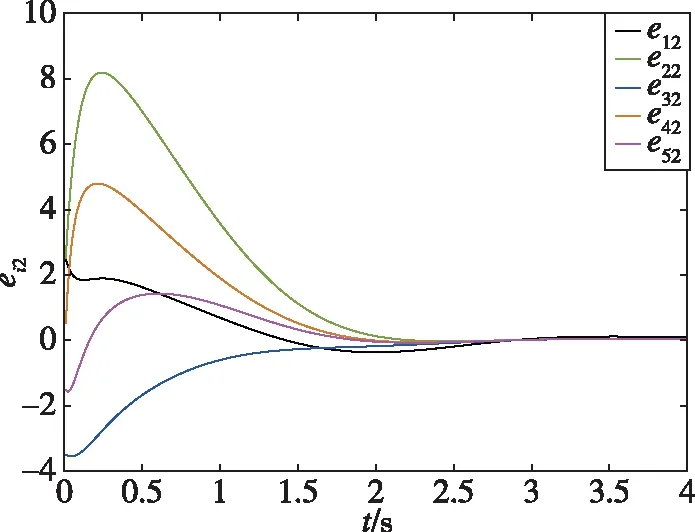
仿真結果如下:圖2所示為智能體0~5隨時間發生變化的狀態軌跡圖,圖3所示為跟隨者1~5與領導者0的狀態誤差軌跡圖,圖4所示為每個跟隨者的控制輸入軌跡圖。從圖2可以看出,跟隨者1、2、3和領導者0的狀態最終趨于一致,而跟隨者4、5和領導者0的狀態最終趨于相反值。從圖3可以看出,同組的狀態差收斂于0,不同組的狀態和收斂于0。從圖4可以看出,由于設計了較大的反饋增益參數,控制輸入量在前0.5s內較大,收斂較快。通過仿真分析可知,在所設計的控制器(19)下,實現了動態領導者下的系統(1)的分組-跟隨一致性控制。圖5所示為系統(1)在反饋控制器()=ξ()時的狀態誤差軌跡,與圖3的結果進行比較,可以發現,在相同時段內本文所設計的控制器可以實現更好的收斂性能。
(a)
(b)
(a)
(b)
(a)
(b)
(a)
(b)
在一定的取值范圍內,,選取的越大,則系統初始時刻的控制輸入量越大,系統的收斂速度越快,控制量曲線越抖。因此,這里需要視情況折中處理,而在理論上選擇的是滿足條件的邊界值。 事實上,存在不滿足假設條件的參數也可以使系統穩定,因為定理1給出的是一個充分條件而非必要條件。
4 結論
本文研究了一類非線性多智能體系統的領導-跟隨一致性控制問題。1)考慮領導者智能體具有非零控制輸入的情況,基于鄰居智能體的相對狀態信息,設計了分布式控制器。2)仿真結果表明,本文設計的控制方案可以使得具有動態領導者的非線性多智能體系統在合作-競爭交互網絡中實現分組-跟隨一致性控制。3)未來的研究工作將考慮時滯影響,在有限時間內實現分組一致性控制。此外,本文設計的控制器是基于連續狀態的,如何設計一個利用離散狀態的脈沖控制器或事件觸發控制器也是下一步的研究方向。

