沖擊加載下氟化鋰晶體熱導率的第一性原理研究*

楊 陳，王 艷，陳南迪，余柏樹，曾召益，劉 勛

(1. 重慶師范大學 物理與電子工程學院，重慶 401331； 2. 南方科技大學 理學院物理系，廣東 深圳 518055；3. 武漢理工大學 理學院物理系，武漢 430070)

0 引 言

氟化鋰(LiF)是一種化學性質穩定的透明絕緣體，熔點為1118 K[1]。在沖擊和靜態壓縮實驗中廣泛應用.當沖擊壓力達到200 GPa時，LiF仍然具有良好的透光性[2]。這使其成為動高壓速度測量和溫度測量重要的窗口材料[3]。因此,研究其在動高壓下的熱導率具有重要的應用價值。

高壓下材料的熱導率研究,在理論方面并不完善.Leibfried和Schlomann在德拜模型基礎上提出了Leibfried-Schlomann方程(L-S方程)[4],認為晶體中絕大部分能量是由聲學聲子傳遞，而晶體缺陷對聲學聲子散射效應影響很小,以及光學聲子對熱傳導的貢獻也可以忽略不計.Roufosse和Jeanloz等[5]先在常壓條件下考慮溫度變化對晶體熱導率的作用,然后在等溫條件下改變壓力研究熱導率的變化情況,推導出了晶體高溫高壓Roufosse -Jeanloz 熱導率方程(R-J方程)。孫峪懷等[6]認為L-S方程中只考慮隨溫度升高聲子平均自由程減小,是考慮不周的。由于動高壓加載技術和測溫技術限制,對于高溫高壓LiF熱導率的實驗研究,相關數據不多見。在靜高壓加載的熱導率測量實驗中,由于溫度加載多屬于對熱導率壓力效應和低溫壓力效應的研究。高壓下熱電偶的標定開始影響實驗的測量結果。為提高實驗測量精度,近年來發展了以光學測量為主導的熱學光柵法[7]。由于該方法受樣品尺寸的限制,加載的最高壓力不能超過40 GPa, 而且高溫高壓條件下,傳壓介質的熱力學性質可能對測量結果有影響。Goncharov小組[8]一直致力于光脈沖加熱技術的高壓熱導率研究工作，由于該方法對激光能量的建模存在較大的不確定度，以及高溫熱輻射也對實驗結果產生較大影響。胡金彪等選用液體CHBr3作為樣品測量高溫高壓下的熱導率,但是實驗數據分析中熱導率系數為理論值,沒有得到實驗驗證。早期美國Ahrens等提出了沖擊壓縮下夾心法熱導率測量技術[9-10]，獲得LiF晶體高壓的熱導率數據,但實驗壓力范圍很窄。趙萬廣等[11]對R-J方程進行參數修正后,在實驗壓力達250 GPa時,測得晶格熱導率與原R-J方程數值相差一倍。由于推導過程不同和實驗條件限制,上述理論變化趨勢和熱導率關系式互相存在明顯差異[9]。

目前,計算晶格熱導率的早期方法有經典分子動力學模擬[12]和弛豫時間近似[13]。其中,經典分子動力學方法主要是采用經驗勢模擬。勢函數的準確性直接影響到計算結果,而勢函數在高溫高壓條件能否適用仍未可知。弛豫時間近似是通過引入弛豫時間(τ)參量來描述散射過程，而忽略了真實的聲子散射[14]。因此,這兩種方法均無法準確的獲得晶格熱導率。本文基于第一性原理計算,結合原子間力常數,采用迭代法求解聲子玻爾茲曼輸運方程,獲得LiF晶體沖擊高壓的熱導率。

1 計算方法

本文中對LiF晶體(空間群Fm-3m)計算總能量的電子結構時,采用的是VASP軟件包中的PAW方法,交換關聯選擇廣義梯度近似的PBE形式。我們將Li的2S1和F的2S22P5作為價電子來處理。在計算中,為了獲得準確的計算結果,我們對k點和q點以及其他相關參數都進行了嚴格的收斂性測試。平面波截斷能均取為500 eV,在靜態能量計算和聲子計算中,分別采取了15×15×15和10×10×10的布里淵區K點取樣。體系總能量的收斂值取了1×10-6eV,原子間力的收斂精度為1×10-4eV/(0.1 nm)。聲子貢獻的熱導率就是晶格熱導率。晶體的自由能F(T.V)可以寫成如下形式：

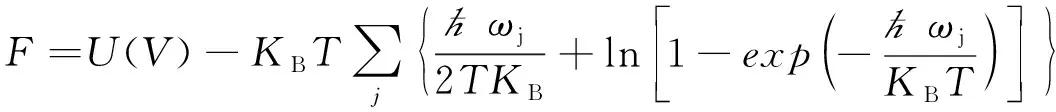
(1)

其中，U(V)是T=0K時晶格的內能,只與晶體體積有關,而與溫度(或晶格振動)無關。后項與晶格振動有關,即與溫度有關。聲子頻率的幾何平均定義為：

(2)

其中，ωqj是波矢q處的第j支聲子的頻率，Nqj是總的聲子的振動模式數目。經測試,以上參數可使聲子的幾何頻率收斂到1 cm-1。在結構優化和自洽計算中采取15×15×15的布里淵區網格點。自洽計算收斂和結構優化完成后，構建4×4×4的超晶胞。采取有限位移法進行聲子譜計算,進而確定二階原子間力常數[15]；在計算三階力常數時,原子間相互作用的截斷半徑經過嚴格測試,為確保結果的準確性,選取原子間六階最近鄰.三聲子散射過程必須滿足能量和動量守恒:

ωj(q)±ωj′(q′)=ωj″(q″)

(3)

q±q′=q″+G

(4)

ωj(q)是(j，q)空間的頻率，當G=0時，稱為正規過程；當G≠0時，稱為翻轉過程。采用ShengBTE[14]程序,迭代求解聲子玻爾茲曼輸運方程[16],從而獲得LiF的晶格熱導率等相關物理性質。晶格熱導率κ可以表示為：

(5)

其中，Ω是原胞的體積，N為原子個數。Cq為熱容量，νq為群速度，τq為聲子壽命。

2 計算結果與討論

2.1 物態方程及聲子色散關系

物態方程是固體能量隨體積的變化關系,描述了固體在壓縮或者拉伸作用下的行為。通過對LiF的靜態能量的計算獲得了物態方程,結果如圖1所示。Liu等[17]在300 K溫度實驗測量了37 GPa范圍內體積隨壓力的變化情況,與Smirnov等[2]的理論結果對比,我們的計算結果與實驗數據更為吻合。物態方程的參數如表1所示,零壓下LiF的平衡體積V0為0.01662 nm3,與實驗值0.01642 nm3接近[17]，體積模量B為72.52 GPa,與實驗值73.0 GPa接近[17]，體積模量對壓力的偏導數B′為4.03，與實驗值3.90吻合[17].彈性常數C11、C12和C44與Briscoe等[18]的實驗數據吻合。

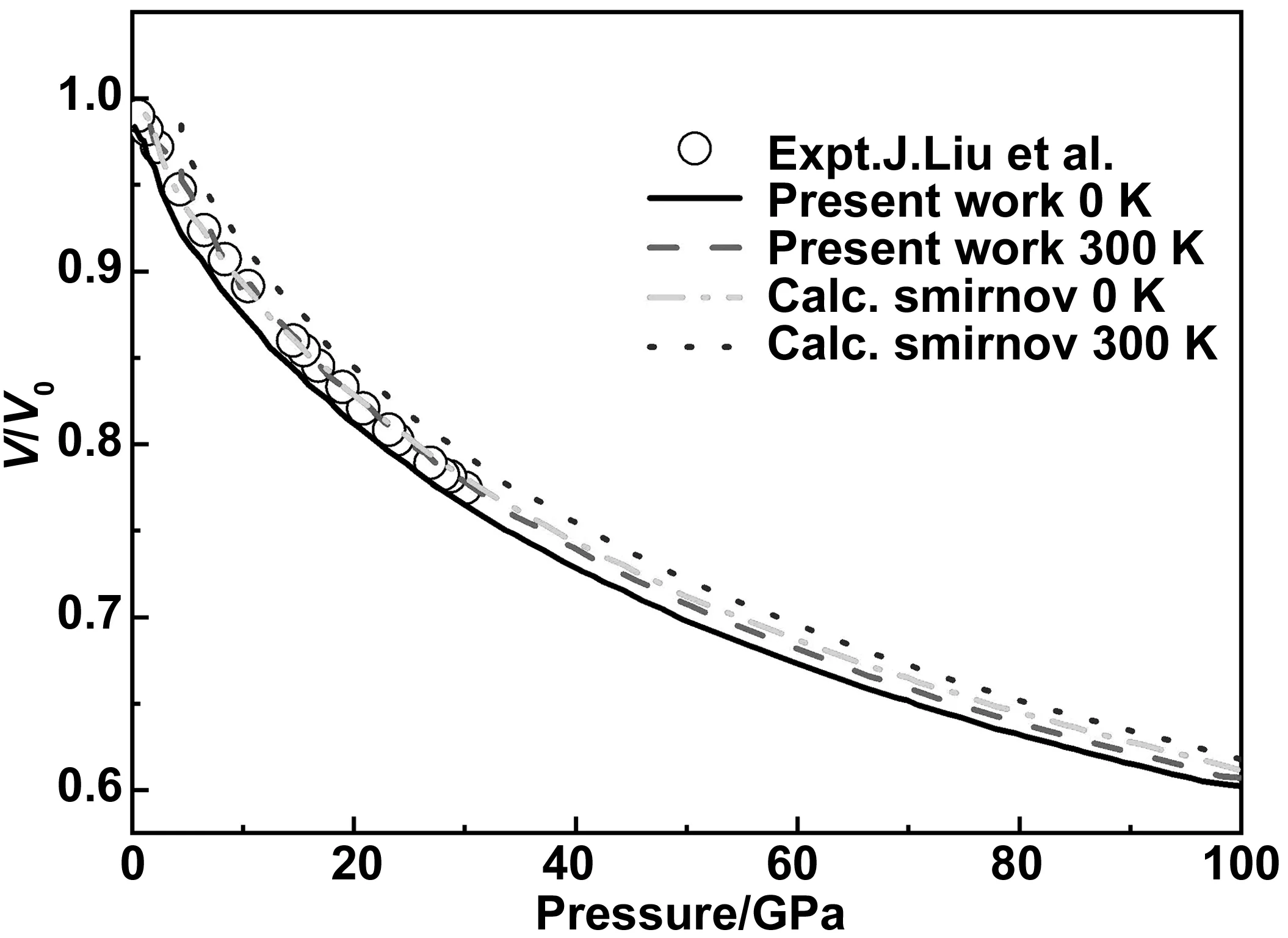
圖1 LiF零壓0 K 和300 K的物態方程,空心圓為Liu等[17]的實驗結果,點劃線和圓點分別為Smirnov等[2]在0 K和300 K的理論結果,實線和虛線分別為本文計算結果Fig.1 Equation of state of LiF at zero pressure 0 K and 300 K ,comparison with experimental data (open circles) of Liu et al [17], and the theoretical results (dot and dash) of Smirnov et al [2], the solid and dotted lines are the results of this paper

表1 零溫零壓LiF平衡晶格常數a(nm)、平衡體積V0(nm3)、體模量B(GPa)、體模量對壓力的導數B′(GPa)和彈性常數C11，C12，C44。

本文采用有限位移方法計算二階力常數,我們獲得零溫下LiF晶體的聲子色散關系，如圖2(a)所示。可以看出聲子曲線沒有出現虛頻,表明晶體結構是穩定的。本文的計算結果與Dolling等[22]實驗結果基本吻合。我們也分別計算了高壓下的LiF聲子色散關系,如圖2(b)所示。從圖中可以看出,隨著壓力的增加聲子頻率峰值上移,沒有出現虛頻現象,表明在本文計算的壓力內LiF一直保持體心立方的穩定結構。通過聲子色散曲線,我們也獲得了高溫高壓下的自由能。

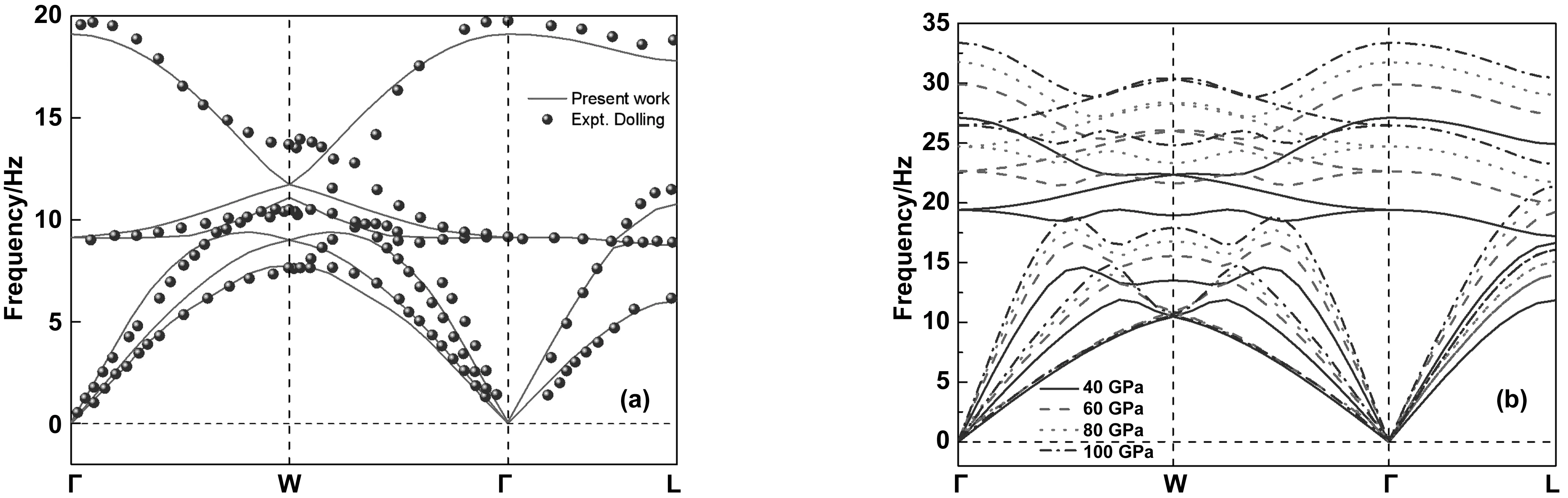
圖2 LiF在零壓(a)和高壓(b)的聲子色散關系,實心球為Dolling等[22]的實驗結果Fig.2 Phonon dispersion relation of LiF at zero pressure (a) and high pressure (b), comparison with the experimental data (solid circles) of Dolling et al [22], the solid line is the result in this paper

2.2 Hugoniot物態方程及聲速

Hugoniot物態方程是材料的重要性質之一,它可以同時反映出材料對壓力和溫度的響應特性。在沖擊波物理中,沖擊壓力PH內能EH和體積VH之間滿足 Rankine-Hugoniot關系:

(6)

式中，E0,P0,V0分別是沖擊加載前初態的摩爾內能、壓力和摩爾體積。EH,PH,VH,分別是沖擊加載后終態的摩爾內能、壓力和摩爾體積。

根據上式,我們計算了LiF的Hugoniot物態方程,如圖3(a)所示。從圖3(a)可以看出,PH-VH隨Hugoniot與實驗結果十分吻合。PH-TH曲線如圖3(b)所示,我們的結果與實驗測量及理論計算的結果基本吻合。圖中空心圓為Kormer等[23]的實驗結果,三角形表示趙萬廣等[11]在改進并完善液體夾心法測熱導率實驗技術后獲得的實驗數據,黑色實線為本文計算結果。我們的結果略低與實驗測量的結果,主要原因在于,在沖擊加載下LiF保持透明性，動高壓實驗無法直接測量沖擊溫度，實驗結果中的沖擊溫度通過熱力學計算獲得，而熱力學計算中相關參數的選擇可能導致沖擊溫度估算過高。

采用直接的應力應變方法,我們計算了LiF隨Hugoniot壓力的彈性常數,如圖4所示。計算結果與Smirnov等[2]的理論結果符合,隨著壓力增大，C11和C12呈線性增加趨勢明顯，C44變化趨勢相對較小。表明在縱向應力的影響下晶胞的拉伸或壓縮程度明顯,體積膨脹或壓縮明顯。將彈性常數通過Voigt-Reuss-Hill 近似計算得到體積模量(B)和剪切模量(G)，壓縮波聲(VP)和體波(VB)聲速。由Hugoniot彈性常數進一步計算得到的Hugoniot聲速如圖5所示,在0 GPa時，LiF的壓縮波和體波聲速分別為7.1 km/s和5.1 km/s,其中壓縮波聲速與劉前程等[26]的實驗數據吻合.隨著壓力增大,壓縮波聲速和體波聲速均增加,且與實驗數據基本一致[26-27]。

圖4 LiF的Hugoniot彈性常數,實心球為Smirnov等[2]理論結果，實線為本文的結果Fig.2 Hugoniot elastic constants of LiF, comparison with the theoretical result (solid circles) of Smirnov et al[2], the solid line is the calculation result in this paper

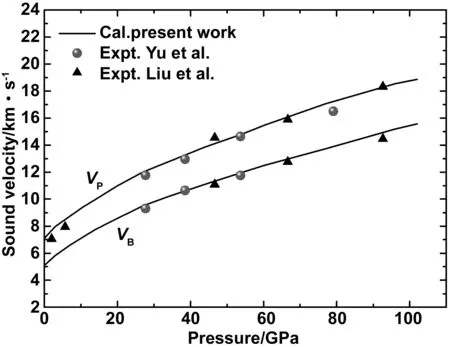
圖5 LiF的Hugoniot聲速實心球和實心三角形分別為Yu等[27]和Liu等[27]的實驗數據,實線為本文的計算結果Fig.5 Hugoniot acoustic velocities of LiF, comparison with the experimental data (solid circles of Yu et al[27], and solid triangles of Liu et al[26]), the solid line is the calculation result in this paper

2.3 晶格熱導率

LiF晶體作為典型的窗口材料,其高溫高壓下的熱導率研究一直是研究熱點。零壓下300～1 000 K范圍內LiF的晶格熱導率如圖6所示。結果顯示，300 K時，結果為12.8 W/(m·K)。2010年Elhadj等[28]實驗得到低吸收系數時晶格熱導率為13.2 W/(m·K), Singh等[29]采用Callaway-Holland模型獲得的結果為13.6 W/(m· K), Liang等[30]采用迭代解求解玻耳茲曼輸運方程的方法得計算值13.89 W/(m·K)。本文計算結果與以上數據符合較好。圖6顯示，隨著溫度升高晶格熱導率降低,當溫度升高到1 000 K時,熱導率降為3.86 W/(m·K).本文計算結果實驗值和其他理論值趨勢一致。

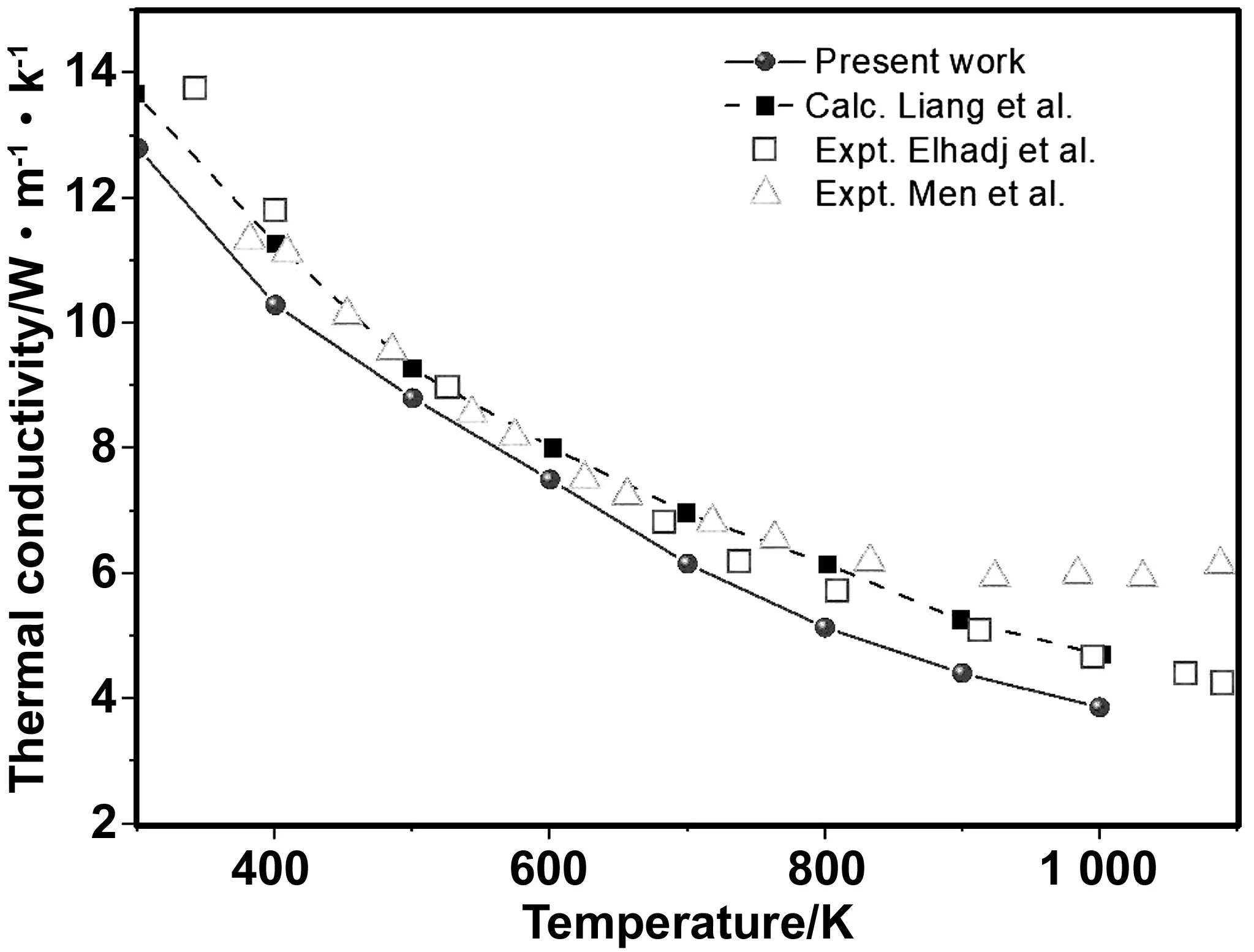
圖6 LiF常壓下300～1 000 K的晶格熱導率，實心正方形為Liang等[30]的理論結果，三角形和空心正方形分別為Men團隊[31]和Elhadj等[28]的實驗數據，實心球為本文結果Fig.6 Lattice thermal conductivity of LiF at 300-1 000 K at atmospheric pressure, comparison with theexperimental data (open square of Elhadj et al[28]and open triangles of Men et al [31]), solid square is the theoretical result of Liang et al [30], solid sphere is the result calculated in this paper

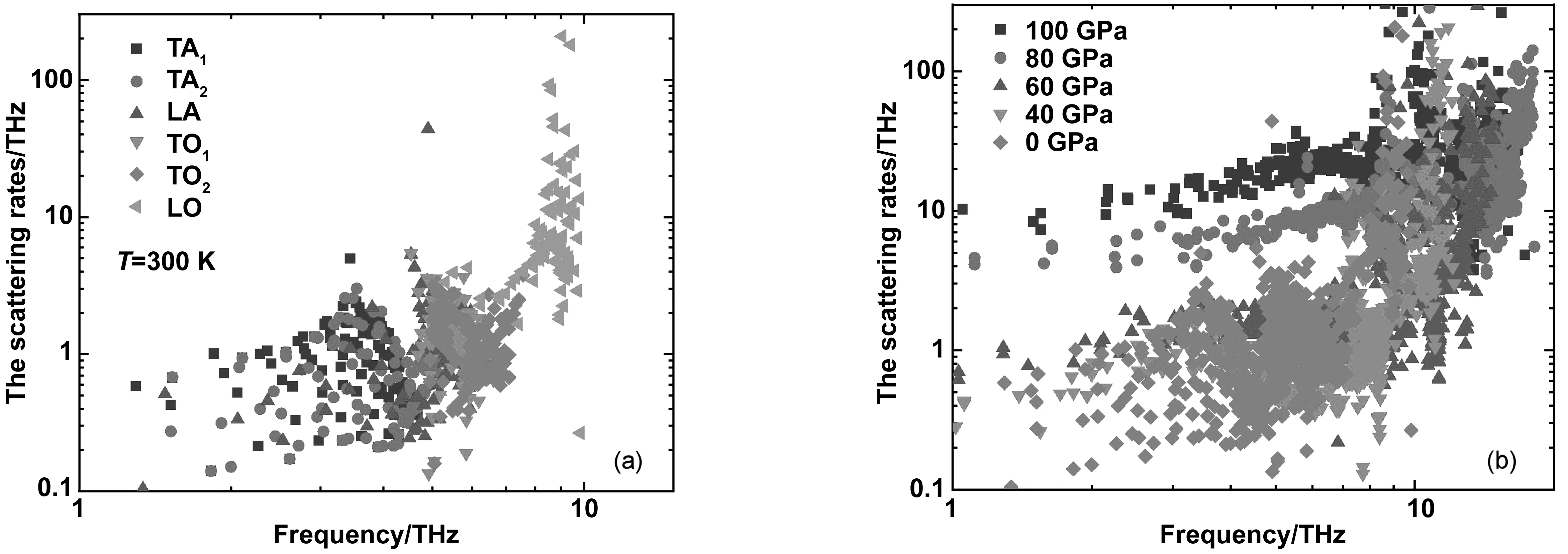
圖7 (a)零壓300 K下聲子散射率,(b)不同Hugoniot壓力下聲子散射率Fig.7 Phonon scattering rates at 300 K at zero pressure and different Hugoniot pressures

趙萬廣等[11]采用液體夾心法熱導率測量技術，結合理論推導給出了修正后的R-J方程。通過數值擬合獲得～39、～70和～100 GPa 3個壓力值的LiF單晶沖擊高壓熱導率數據，分別為13.2±1.0、7.1±1.4和4.8±0.6 W/(m·K) (這3個數據點是實測數據，先有的實測數據，再根據實驗結果修正的R-J方程)。與本文的計算結果的變化趨勢一致,如圖8所示。結果表明，LiF晶體在動高壓沖擊100 GPa范圍內,熱導率先緩慢增加后快速降低,40 GPa附近達峰值。出現這種現象主要是受聲子非諧散射效應的影響,散射率越低，聲子壽命越長,從而具有較大的晶格熱導率。 壓力較低時，我們的計算結果遠高于實測結果，壓力較高時，二者則趨于一致，造成這種差異的具體原因尚不清楚。需要指出的是，雖然趙萬廣等[11]采用的液體夾心法熱導率測量技術比早期Ahrens等[9]的實驗方法有所改進，但在得出LiF熱導率的過程中還是使用了一些經驗參數，如高壓下三溴甲烷、LiF的定容比熱及LiF的格林艾森參數等，這些熱力學參數的選取會影響最終的實驗結果。

圖8 Hugoniot熱導率,實心球為趙萬廣等[11]的實驗數據，方形為本文的計算結果，實線為線性擬合結果Fig.8 Obtain lattice thermal conductivity along the Hugoniot, comparison with the experimental data (solid sphere) of Zhao et al[11], the square is the result of calculation and the solid line is the result of linear fitting

3 結 論

基于第一性原理晶格動力學方法，通過求解聲子的玻爾茲曼輸運方程，獲得了高壓下LiF晶體的Hugoniot物態方程和Hugoniot晶格熱導率。高壓下聲子色散關系結果表明LiF晶體在計算的壓力溫度范圍內一直保持體心立方穩定結構。采用準諧近似的方法,計算獲得的Hugoniot物態方程與早期的理論結果及實驗數據符合較好。采用迭代解方法求解聲子的玻耳茲曼輸運方程，準確計算了100 GPa,2000 K范圍內LiF晶體的晶格熱導率,在3個壓力值～39、～70和～100 GPa的實驗數據分別為13.2±1.0、7.1±1.4和4.8±0.6 W/(m·K)，與計算結果的變化趨勢一致.最后預測的LiF沿Hugoniot線的晶格熱導率將為動高壓溫度測量提供重要的參考數據。