基于切比雪夫擬合的BP自聚焦算法

李彥君，劉 佳，徐秋鋒

（北京遙感設備研究所，北京 100854）

0 引 言

合成孔徑雷達（synthetic aperture radar，SAR）是一種主動信息探測工具，通過發射寬帶信號實現距離維高分辨，同時利用天線與目標相對運動產生的多普勒帶寬實現方位維高分辨，由于良好的工作特性，被廣泛應用于各種運動平臺環境探測中。合成孔徑成像算法在拋物軌跡運動下需要精確的運動補償來抵消距離徙動（range cell migration，RCM）和方位相位誤差（azimuth phase error，APE），雷達運動參數的測量常通過在系統上加裝導航裝置來實現。由于實際運動的氣流擾動、平臺機械振動以及復雜軌跡帶來的相位誤差較大，難以只依靠導航裝置消除距離測量誤差，還需要進一步的聚焦算法來處理超出導航設備測量精度的運動誤差。后向投影（back-projection，BP）成像精度高，適用于復雜軌跡下的成像，在實際拋物軌跡運行下仍需通過聚焦處理達到成像要求精度。成像的自動聚焦算法是一種基于回波數據的算法，適用于相位誤差估計，在SAR成像中起著非常重要的作用。

考慮到拋物軌跡運動帶來的運動誤差以及硬件帶來的精度限制，需要采用自聚焦算法進行成像數據處理。傳統的自聚焦算法有基于圖像質量與相位梯度下降兩類。基于圖像質量的一種自聚焦算法，主要評估標準是有關圖像的一般信息，評估圖像質量的主要標準包括最小熵、最大對比度和最大清晰度，通過設置估計的相位值來確定相移以獲得最佳圖像質量。另一類自聚焦算法是相位梯度自聚焦算法，該算法使用多個目標點的相位歷史來估計相位誤差。第一種自聚焦處理基于整體的圖像信息，具有更好的魯棒性，適用于低信噪比與低對比度的成像處理。

傳統的自聚焦算法的實現應基于以下兩個條件：

（1）包絡誤差對圖像的影響可以忽略不計；

（2）在距離的相位上的歷史數據與獲得的結果之間存在傅里葉變換關系。

傳統BP成像算法是全時域成像算法，由于時域成像算法處理信號中不包含明顯傅里葉變換關系，因此無法將兩種傳統的自動聚焦方法直接應用于BP成像算法。文獻［15-17］對BP成像中的信號性質進行了分析，表明當BP算法在極坐標或偽極坐標格式下處理的時候，在距離的相位上的歷史數據近似滿足條件（2）。在此情況下，可以針對（偽）極坐標下的圖像設計相應的自聚焦算法。

近年來提出的新的聚焦處理還有一類是基于機器學習算法的處理，利用機器學習中對于參數求解的思路，得到誤差修正量使得某一圖像質量指標達到最大。但該類算法往往需要較大的運算量，并不適用于實時BP成像處理。

為了彌補上述不足，本文提出了一種針對SAR在拋物軌跡下的BP成像聚焦算法，不依賴于傅里葉變換對關系，且可快速實時地進行時域自聚焦處理。其適用于拋物線軌跡下BP成像結果的實時處理，實現了BP圖像在直角坐標系下的自動聚焦。本文首先結合拋物線軌跡介紹了BP成像算法原理，分析了成像過程中的相位誤差，并用切比雪夫擬合的回波信號進行數字信號分析處理，給出了合適的表達式后對改善的BP成像聚焦效果進行了分析，最后仿真結果對比表明在拋物軌跡下BP自聚焦算法提高了成像效果。

1 BP成像誤差分析與聚焦標準

1.1 BP成像誤差分析

拋物線軌跡下聚束SAR的成像幾何如圖1所示。

圖1 拋物軌跡SAR幾何模型Fig.1 Parabolic trajectory SAR geometric model

雷達平臺在如圖1所示的笛卡爾三維坐標系內運動，在平面內沿平行于軸進行加速運動。設方位向的運動速度為v ；方位向慢時間為t ；距離向快時間為t ；合成孔徑中間時刻平臺所處的位置為點；定義點位置的時刻為方位零時刻；點是該天線波束覆蓋區域的中心點；為點到平臺的斜距；為平臺高度。可以求得對應的水平距離向以及方位向的快時間函數（t，）、（t ，）。雷達平臺經過點沿軌跡運動到點位置，此時對應的距離為根據慣性導航補充的信息推導出瞬時傾斜距，具體以聚束模式下成像為例，在點位置根據距離向以及方位向的瞬時距離可得

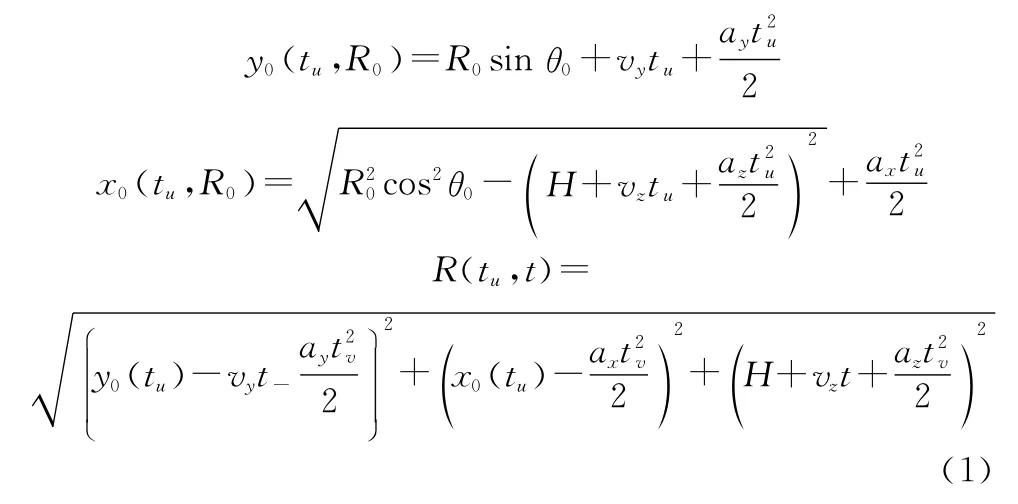
BP成像適合高分辨率低頻超寬帶或寬波束SAR的成像處理。不考慮幅值衰減和天線加權情況，發射的線性調頻信號為

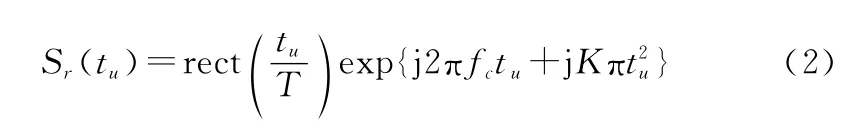
式中：t 為方位向慢時間；t為距離向快時間；為雷達信號脈沖寬度；f 為載頻；為發射信號的線性調頻率。接收到的回波信號由于測量成像區目標的距離產生時間延遲，在目標點的實際距離為（t，t ），回波可以表示為

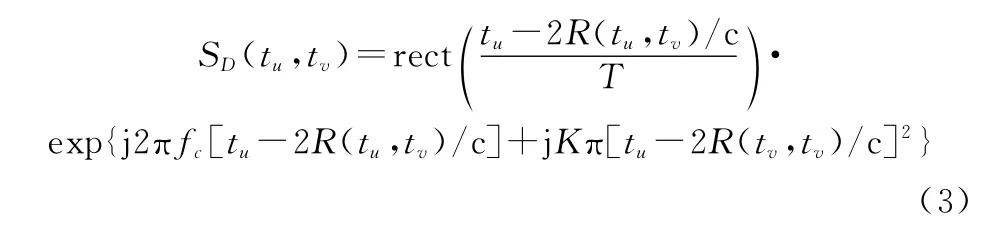
式中：c為光速。經過距離為（t，t ）地面反射后，對回波信號進行脈沖壓縮，即對回波脈壓之后的等效匹配濾波信號為

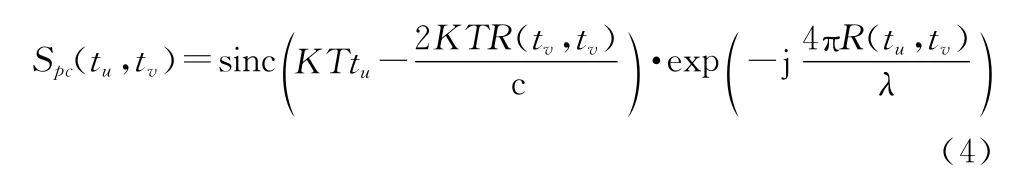
式中：＝c／f 表示發射信號的波長。成像區域的信號經處理后獲得一個×的距離方位二維數據矩陣，位于矩陣中的每一元素（M ，N ）均可以得出精準的距離歷程函數。將此函數處理后，可得成像目標點的脈壓回波數據對應的幅度，將回波進行相干后可獲得SAR雷達圖像，具體公式為

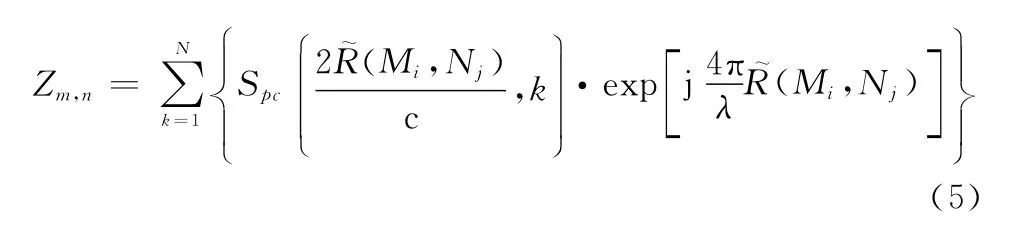
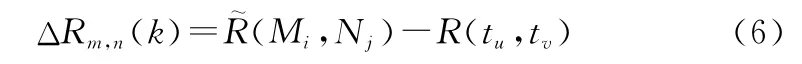
由測量距離與實際距離的差值產生的誤差ΔR（）將對成像信號產生干擾：

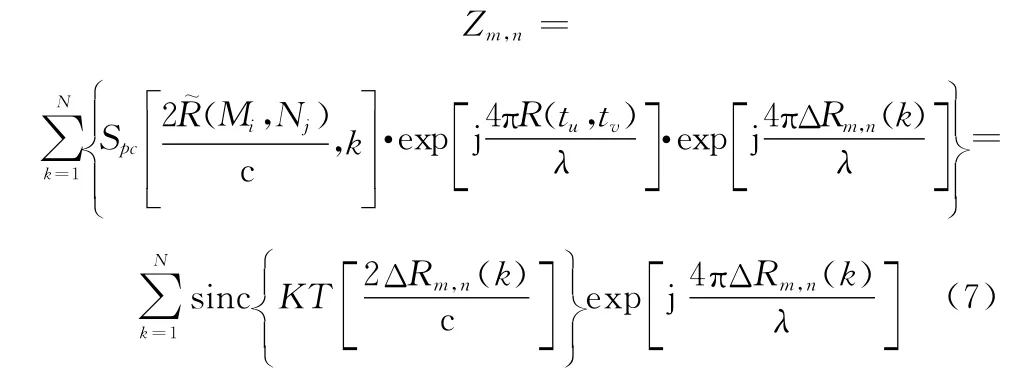
ΔR（）帶來的誤差來自匹配后辛克函數的偏移以及指數函數相位偏移帶來的畸變，對成像的像素矩陣產生了散焦效應。聚焦的目的主要是消除ΔR（）帶來的誤差，提高成像圖像質量。

1.2 聚焦處理標準

對于BP成像算法而言，現有的成像后聚焦采用的標準是以成像圖特征為標準，例如最大對比度、最大標準差等。自聚焦處理一般做法是遍歷所有成像處理后的聚焦點，判斷成像圖的性質，使得成像停留在圖像性質最高的聚焦位置上。相位梯度自聚焦（phase gradient autofocus，PGA）算法需要完整的成像矩陣信號來進行處理，需要進行多次迭代。以圖像特征為標準的聚焦處理忽略了成像信號中相位所包含的誤差信息，為成像后處理（即在生成圖像后進行針對圖像的處理），文中采用針對成像信號的聚焦算法可以貼合雷達成像算法實現實時處理。對于本文提出對成像信號進行的聚焦處理，采用針對單點信號處理前后的積分旁瓣比（integral side lobe ratio，ISLR）以及峰值旁瓣比（peak side lobe ratio，PSLR）進行聚焦效果的衡量，并且加以反演面目標的聚焦前后的圖像指標分析，予以聚焦算法有效性的佐證。

由式（7）可知，誤差ΔR（）存在于成像信號Z的辛克函數以及其指數函數中。為了獲得ΔR（）從而消除干擾以實現聚焦，選擇Z中包含ΔR（）的相位信息作為聚焦處理目標，基于成像信號的自聚焦是通過分析相位函數性質估計每一方位向的相位誤差?的處理。雷達成像為方位向與距離向對成像目標的脈沖壓縮處理，故可以采用PSLR與ISLR為聚焦標準，PSLR定義為主瓣峰值與10倍主瓣寬度范圍內最大旁瓣的功率比值，用于信號脈沖壓縮后對信號的評估。ISLR是主瓣能量與旁瓣能量之比，單位以分貝表示，同樣用于衡量脈壓之后信號的評估。圖像熵（image entropy，IE）代表整個圖像的能量聚焦度，熵越小圖像的聚焦度越高。而圖像空間頻率（image spatial frequency，ISF）和圖像平均梯度（image average gradient，IAG）則表明了圖像的細節，圖像標準差（image standard deviation，ISD）表征了圖像離散度。

Z為所有方位時刻一個像素點的相干累積結果，所有方位時刻與網格距離補償結果進行疊加等效于對該點方位向的函數進行脈沖壓縮。ΔR（）的存在會影響方位向的等效脈壓，從而導致方位向的散焦較嚴重。對每一時刻的像素點疊加進行補償，即對BP算法進行內部算法修正實現聚焦處理。

辛克信號在成像區間內符號不一致會影響距離誤差ΔR （）的估計精度，為消除其影響，同時保留了指數函數中的ΔR （），構造信號估計函數G：

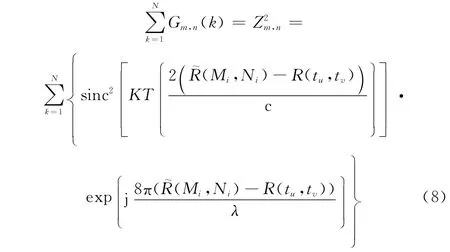
對于每一方位時刻像素點，在BP算法進行方位時刻累加前，即脈沖壓縮后存在：

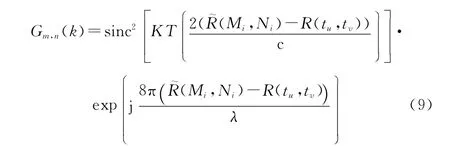
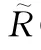
經處理后得到的ΔR（）相關的相位構造補償相位矩陣，與每一方位時刻成像矩陣進行數乘再進行時刻累積，即得到消去ΔR（）干擾的聚焦圖像。同時根據距離誤差與補償相位參數關系，考慮匹配之后的辛克函數以及指數相位函數的性質，可以構造補償參數Z（）。在補償相位誤差的同時，提高成像之后辛克函數的PSLR，解決散焦現象，加強成像點區分度。

2 BP成像算法的自聚焦算法

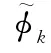
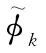
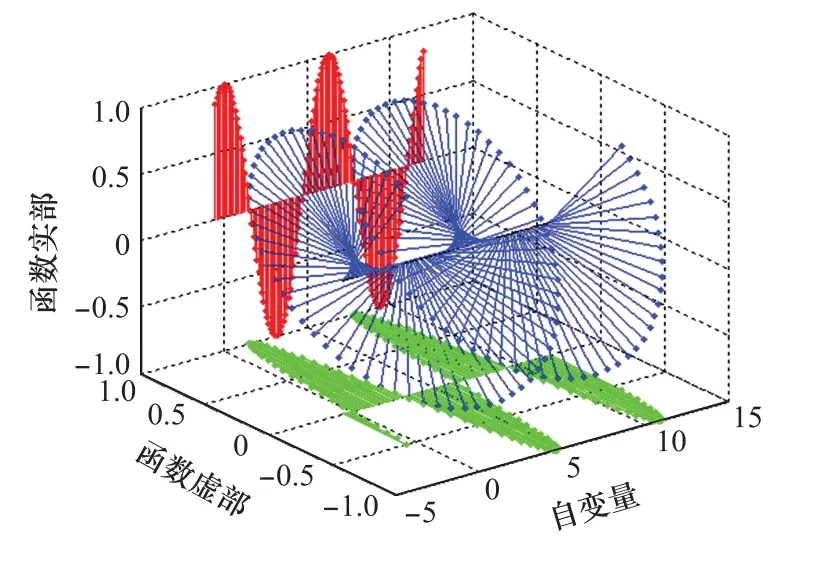
圖2 方位向函數復數域投影Fig.2 Azimuth function complex number domain projection

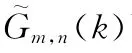
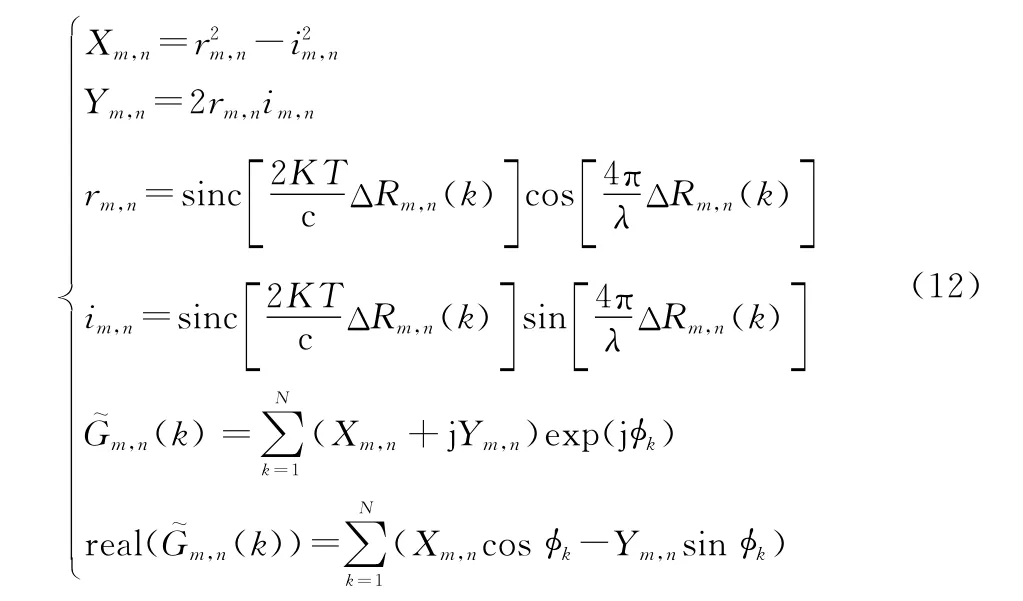
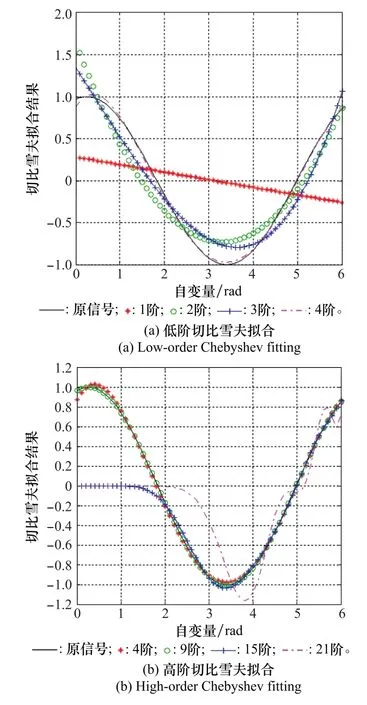
圖3 切比雪夫擬合余弦函數圖Fig.3 Chebyshev fitted cosine function graphs

由階數與擬合效果可見，低階擬合誤差過大、高階造成過擬合，同時考慮處理的數據量以及時效性，二者主要由擬合的階數決定，擬合階數越高，所需的擬合數據量越大，涉及運算越復雜、時效性越低。具體參數如表1所示。

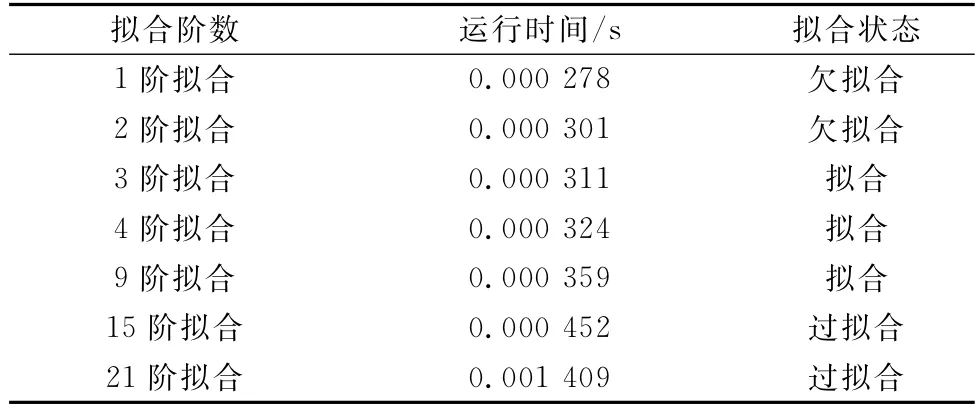
表1 切比雪夫擬合處理時間Table 1 Chebyshev fitting processing time

通過切比雪夫擬合定義的多項式正交，當?滿足限定條件［-π，π］時，求解四階切比雪夫系數，得到對應的多項式系數可以表示為

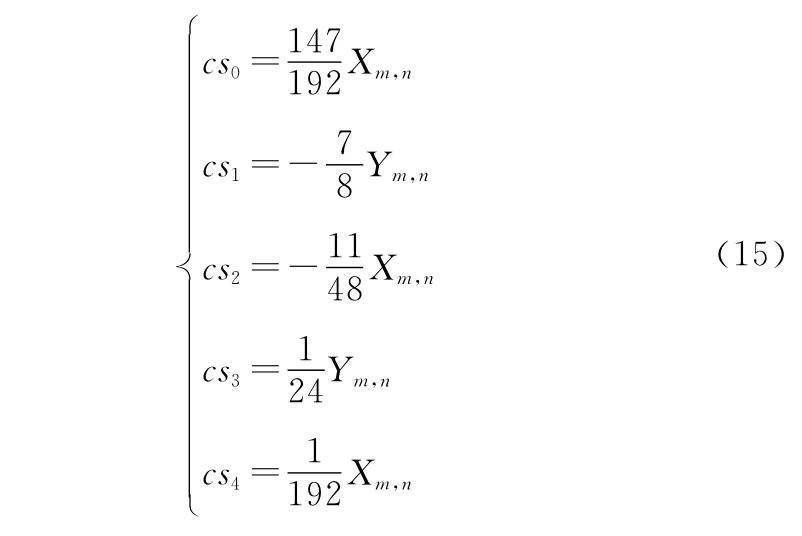
研究對應?的四次函數需要將已知數據即X 與Y 與未知數據?拆分開來，轉化為僅與?有關的四次函數，式（14）與式（15）通過轉化可以得到如式（16）的四次函數（?）：

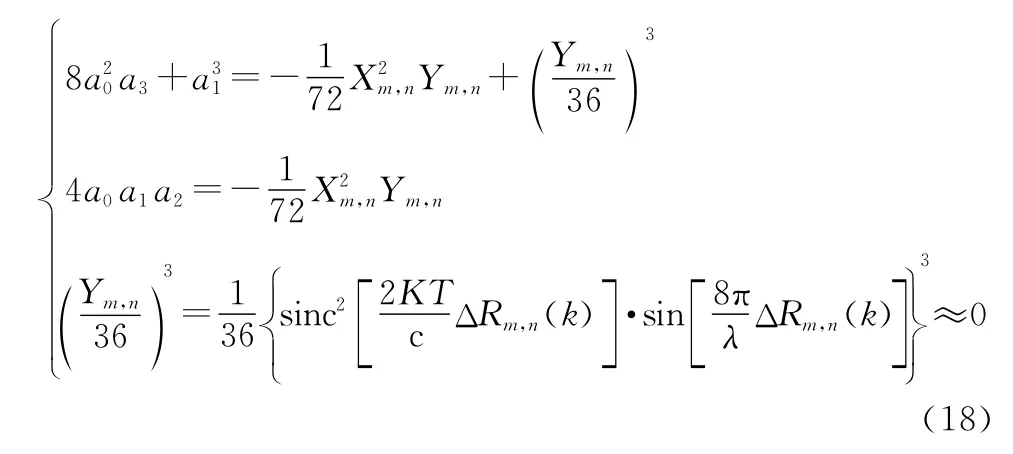
得出經過切比雪夫擬合后的四次函數滿足對稱條件。對于四次對稱函數而言，根據文獻［26］中定義可知：

結合式（21）、式（17）、式（18）可得對應的參數，具體表示為

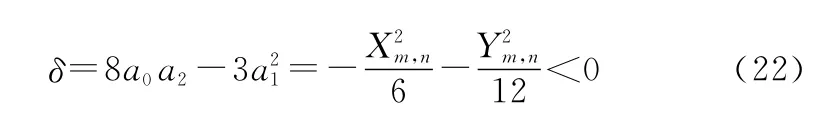
由文獻［27］中所提的四次函數性質可知，對于＜0，需要根據與0的關系判別擬合后四次函數的最值點位置關系。根據之前所得的擬合多項式的四次函數形式，由性質可得，最值點位置為

將得到的補償函數代回每一方位時刻中，通過補償函數的辛克函數對誤差產生的旁瓣進行抑制，同時補償函數中的指數函數補償由距離誤差產生的相位畸變，結合補償函數的辛克函數與指數函數得到修正后信號，進行方位時刻積累得到成圖數據：

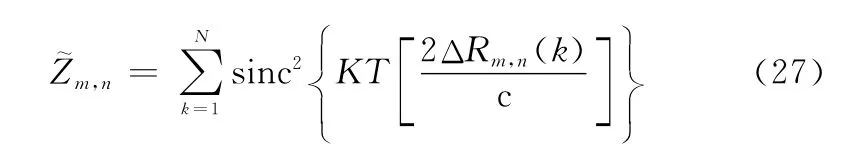
為了說明聚焦算法處理的有效性，雷達接收數據進行成像及自聚焦處理的流程如圖4所示，通過雷達運行平臺裝備的導航器件對距離誤差進行修正，修正得到的數據進行切比雪夫擬合，對擬合后四次方形式的函數進行信號分析，處理得到誤差參量，代回修正函數與運動補償后數據，進行相乘后進行方位向累加，得到聚焦雷達成像圖。

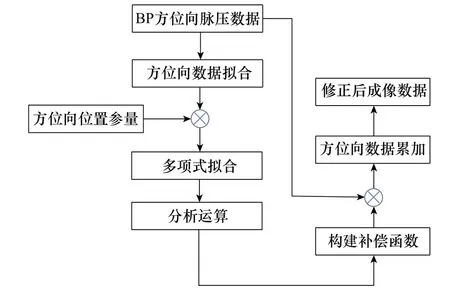
圖4 聚焦處理算法流程圖Fig.4 Focus processing algorithm flow chart

3 仿真結果與分析

本文算法的有效性通過點目標聚焦處理前后的PSLR以及對仿真場景的面聚焦結果對比來說明。仿真雷達系統的參數如表2所示。

表2 仿真參數Table 2 Simulation parameters

3.1 聚焦算法有效性驗證

本文提出的聚焦算法是對成像信號Z存在ΔR情況下，基于信號分析進行的處理。需要通過算法信號得到對應方位補償參數（），并構造修正函數，進而消除ΔR干擾，去除相位模糊，并提高PSLR，以三方位向點目標的成像信號為例進行算法分析比較。

對成像算法信號進行聚焦，經過信號處理為基礎的聚焦運算后得到的成像信號與未經過處理的成像信號如圖5所示。點目標經處理之后的方位向歸一化旁瓣比見圖6，可以看出處理前后的峰值與旁瓣間有明顯的差異，信號處理加強了PSLR從而提高了BP算法對成像信號的方位向脈壓效果，成像信號的PSLR有所提升，對于單點目標的回波信號質量有改進。根據點目標結果進行聚焦處理前后成像信號參數對比，聚焦運算處理后的PSLR以及ISLR明顯提高，可以看出經切比雪夫擬合以及信號處理的相位補償函數有效地抑制了方位向散焦，PSLR及ISLR的改進效果如表3所示。表3表明了在聚焦處理評價標準下，本文提出的算法處理效果較好。

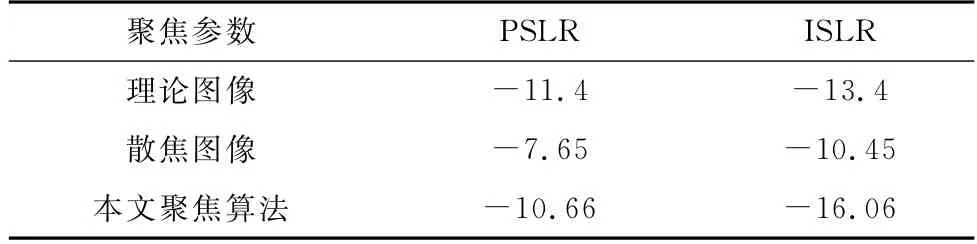
表3 仿真結果Table 3 Simulation results d B

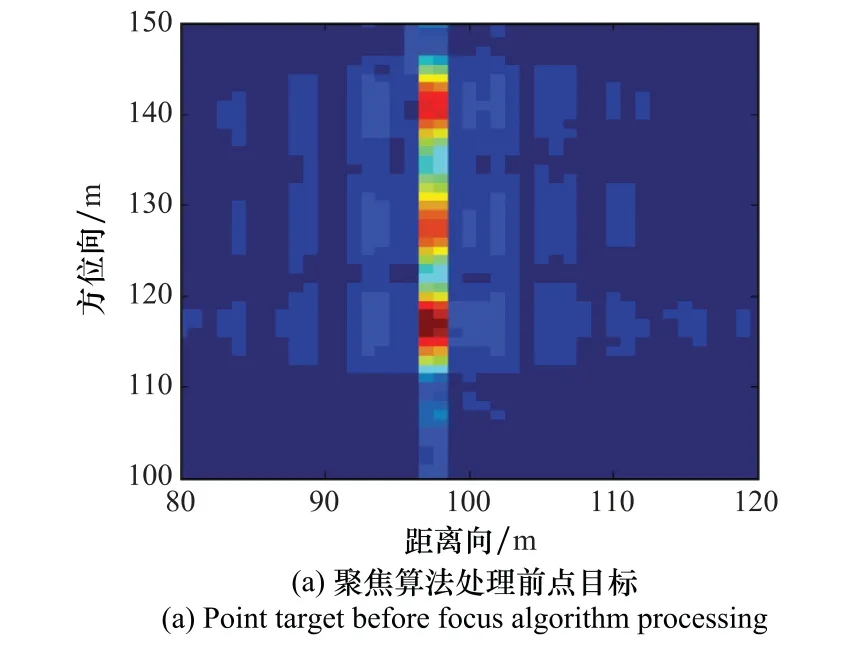
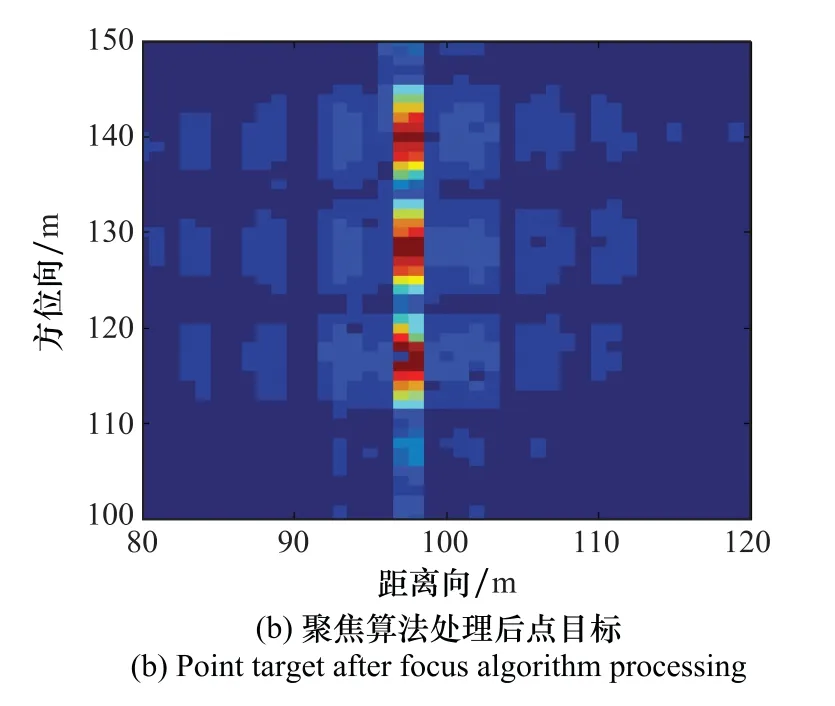
圖5 聚焦算法處理前后點目標對比Fig.5 Comparison of point target before and after focus algorithm processing

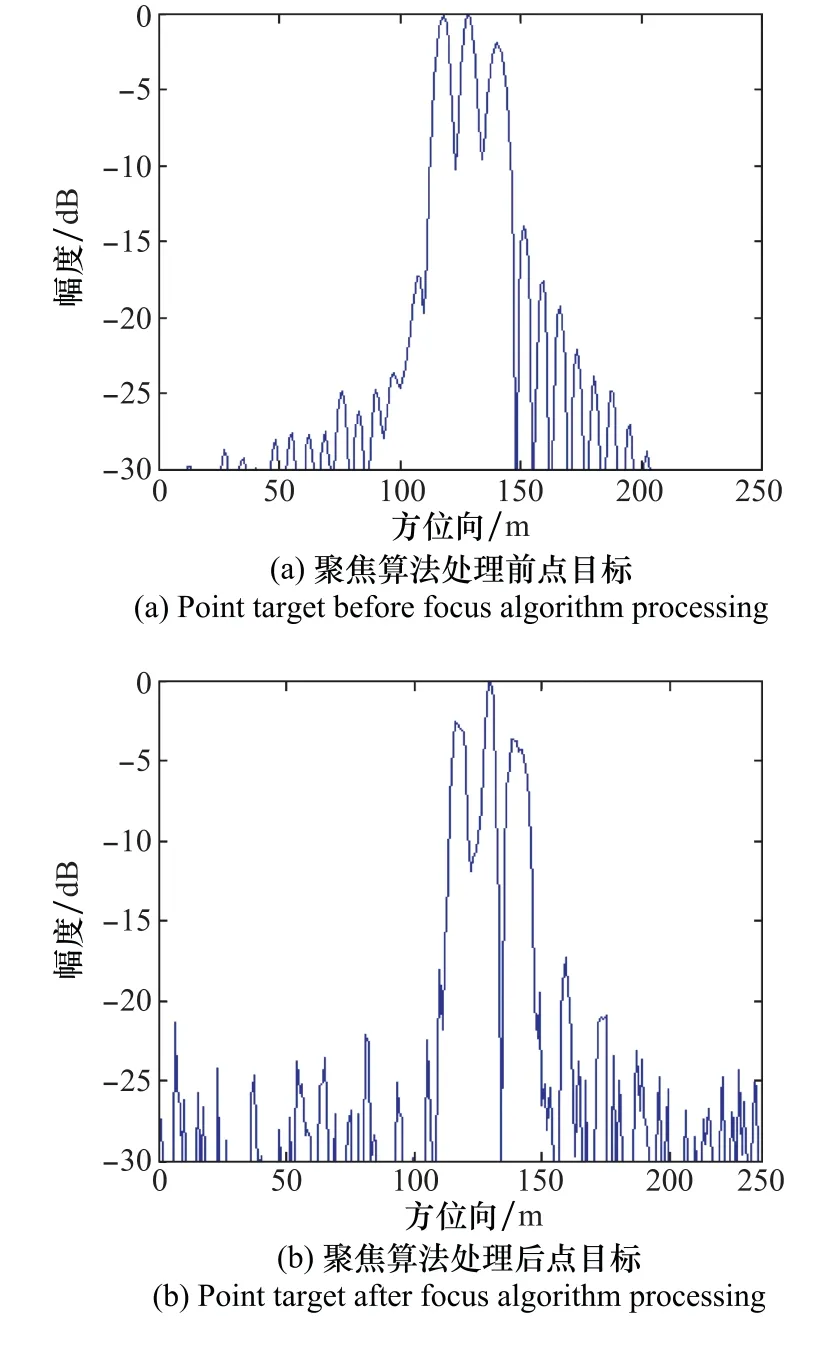
圖6 點目標聚焦前后歸一化幅度Fig.6 Normalized amplitude of point target before and after focusing

3.2 聚焦算法對比

本文算法對BP算法所成的圖像可有效地進行估計補償，圖7為在表2參數設計下的雷達仿真平臺，采用高分三號的雷達圖進行反演得到面目標回波信號，并用其對算法進行對比運算。對反演面目標進行的仿真結果，成像區域大小為256×256 m，運行速度與加速度同表2中一致，面目標成像采用本文的聚焦算法處理后圖像質量有所改善。對于面成像的評價指標依據IE、ISF、IAG、ISD，具體結果如表4所示。

圖7 聚焦算法處理前后面目標對比Fig.7 Comparison of surface targets before and after focus algorithm processing

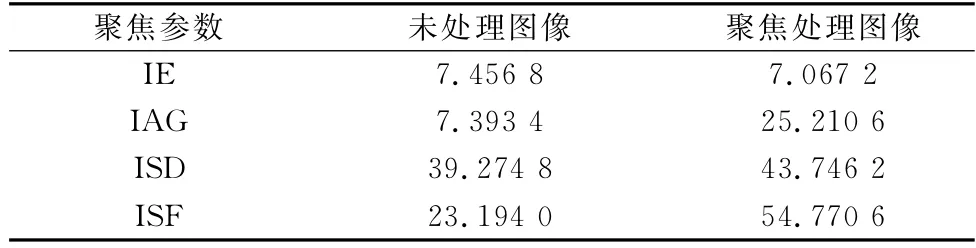
表4 面成像評價指標Table 4 Surface imaging evaluation indicators

如表4所示，聚焦處理后的IE更低，表明處理后的圖像聚焦度高于處理前；IAG在處理后增加，表明像素間能量差異變陡峭，更好地顯示細節；ISF同理，表明處理后的圖像具有更好的細節。與其他基于BP算法的自聚焦處理算法對比，文獻［28-29］中的自聚焦算法雖可以理想地聚焦處理，但相比于本文所提算法，具有較高的計算量，對于要求實時處理的拋物軌跡的雷達系統并不適用。對于文中提及的聚焦處理，運算復雜度低于PGA算法，且本算法處理嵌合于BP算法處理流程中，并不屬于圖像后處理，生成圖像后還可以進行后續的基于圖像的聚焦算法處理。處理面目標結果如圖8所示，與PGA算法處理結果參數對比如表5所示。

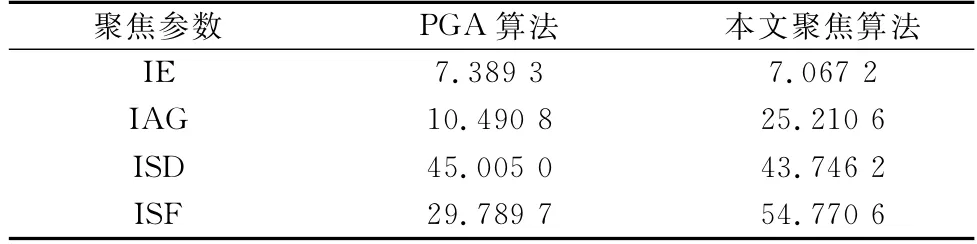
表5 聚焦算法對比Table 5 Focus algorithm comparison

圖8 聚焦算法對比圖Fig.8 Focus algorithm comparison graphs

對比傳統自聚焦算法，以參考文獻［30-31］中的PGA聚焦算法為例，PGA算法以最小二乘法對誤差相位梯度估計，利用傅里葉關系求導且需要較高的信雜比。算法運行中需要多次的迭代，運算量較大，PGA屬于后處理算法，不能加在成像過程中實時處理。對比于以機器學習算法為基礎的新聚焦算法，本文提出的聚焦處理更加適合實時性實現，與傳統的聚焦算法相比，本文的聚焦算法效果有更好的補償精確性。

4 結束語

自聚焦算法是復雜軌跡下SAR成像過程中不可缺少的處理過程。對于采用BP算法生成的SAR系統，提出了一種適合于拋物軌跡下基于切比雪夫參數擬合的成像自聚焦算法。首先對相位誤差在BP算法中的存在形式進行了分析，然后基于數字信號分析給出了聚焦處理修正函數的優化模型。算法結合信號分析以及數值分析的切比雪夫多項式擬合，在BP成像的數字信號處理流程條件下，可以有效地提高成像的質量，本文提供了算法的數學推導和仿真結果。根據理論結果，對成像目標分別采用點目標以及反演面目標回波驗證算法，證明聚焦算法提升了圖像效果。下一步將考慮進一步提高運算效率以及聚焦算法性能，并考慮實現應用于三維成像算法的聚焦處理中。