舵機動態響應下導彈阻尼回路穩定性

周志明，劉 振，*，易建強，姚曉先

（1.中國科學院自動化研究所，北京 100081；2.北京理工大學宇航學院，北京 100081）

0 引 言

導彈一般氣動阻尼不足，欠阻尼特性導致彈軸長時間擺動，對導引回路的工作將產生不利影響。因此，采用阻尼補償回路增強彈體阻尼性能的方法普遍應用于各類導彈的控制系統中［1-3］。但是，控制與制導回路的作用也引起了一系列導彈穩定性問題。

目前，國內外對各類導彈的動態穩定性研究已有很多成果，尤其在旋轉導彈領域［4-10］。特別地，針對控制回路，Yan等首先研究了阻尼回路對旋轉彈角運動的影響，指出旋轉彈阻尼回路增益上限比非旋轉彈低很多［11］，隨后推導了使用姿態駕駛儀滿足錐形運動穩定條件時，阻尼反饋增益和姿態反饋增益需滿足的動態關系［12］。Li等人更進一步推導了采用兩回路和三回路過載駕駛儀的旋轉彈角運動穩定性條件［13-15］。Zhou等人從飛行試驗中的異常現象出發，研究發現鉸鏈力矩作用下的舵機響應有可能會誘導不穩定的錐形運動［16-17］，并且進一步研究分析了舵機傳動間隙對旋轉彈錐形運動穩定性的影響［18］。針對制導回路穩定性的分析同樣有許多可借鑒的工作［19-23］，Hu等人重點分析了采用尋的三維比例導引的旋轉彈穩定性準則，并且分析指出轉速越大，脫靶量越大［24］。Zheng等人和Tian等人在此基礎上，研究了采用比例導引，并考慮導引頭隔離度寄生回路下旋轉彈的錐形運動穩定性［25-26］。Hu等人特別地考慮了捷聯式導引頭響應滯后引起的旋轉彈穩定性條件變化情況［27］。然而上述文獻在制導控制回路建模中，均僅考慮了舵機的穩態響應，沒有考慮舵機動態響應過程，這樣所得到的導彈的穩定性條件可能與真實情況存在一定的偏差。在研究無控段舵機鉸鏈力矩對旋轉彈動態穩定性的影響時，Yousof等人首次指出舵機的動態響應使得控制參數穩定域會發生偏移［28］，修正了Zhou等人的結果，具有一定的啟示意義［16］。近期，Fan等人考慮舵機的動態響應，給出了各參數對兩回路過載駕駛儀參數穩定域的影響［29］，具有很大參考意義。綜上，雖然對于導彈制導控制回路穩定性分析的文獻很多，但是考慮舵機的動態響應對制導與控制回路的作用，并對導彈的動態穩定性的研究依然較少。

本文建立了阻尼駕駛儀控制的導彈動力學方程以及舵機的動力學方程，采用勞斯判據，對比研究了非旋轉導彈在舵機穩態與動態響應下阻尼反饋增益的穩定區域，進一步采用復姿態角方法和Lyapunov穩定性判據，研究了旋轉彈阻尼回路動態穩定性條件，對工程實踐具有一定的指導意義。

1 導彈動力學與舵機模型

旋轉導彈的動力學方程參照相關文獻［15，29］可以描述如下，其中非旋轉導彈認為轉速＝0。

舵機模型參照周偉［18］建模方式建立，考慮舵機系統常用的比例微分（proportional derivative，PD）控制器，其中比例系數為KP，微分系數為KD，記舵機的指令為δc，舵機的響應為δ，即U＝（K P＋K Ds）（δc-δ），可以得到舵機的響應與指令之間的傳遞函數為

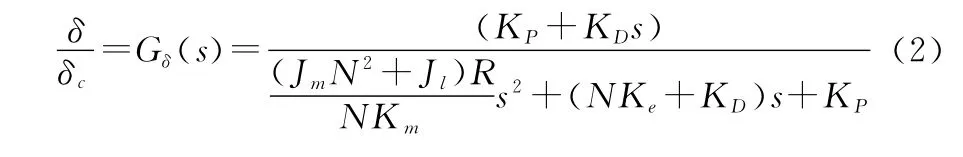
一般的舵機系統為避免系統因反饋噪聲信號引起震蕩，K D取值通常較小，在K D＝0時，系統為簡單的比例控制器，則舵機的響應與指令間的傳遞函數化簡為

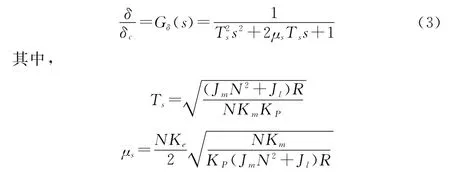
式中：Jm為電機轉軸轉動慣量；J l為舵片轉動慣量；N為減速器的減速比；R為電阻；K e為反電動勢系數；K m為電磁力矩系數。可以看到，舵機響應為被建模成一個二階環節。

表1 參數定義表Table 1 Nomenclature

2 非旋轉彈阻尼駕駛儀穩定性

當＝0，彈體不旋轉，馬格努斯力和力矩以及慣性力矩參數項均為零，非旋轉彈俯仰和偏航沒有耦合，以俯仰方向為例，非旋轉彈的動力學方程為

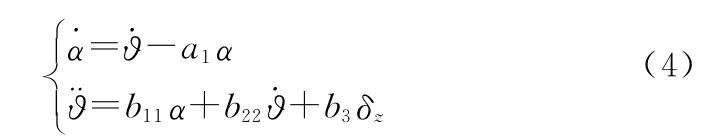
非旋轉彈俯仰方向阻尼回路如圖1所示。

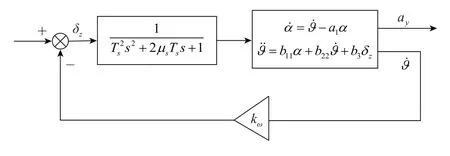
圖1 非旋轉彈阻尼回路結構圖Fig.1 Structure of non-spinning missile damping circuit

據圖1可得，非旋轉彈姿態角在阻尼回路作用下的動態響應為

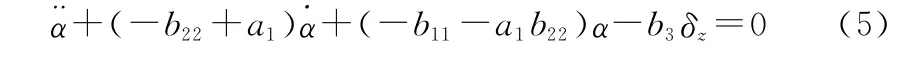
若忽略舵機的動態響應過程，只考慮穩態響應的情況下有

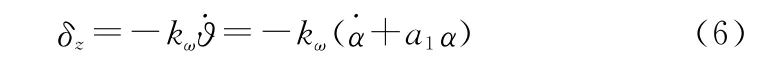
則舵機穩態響應下的攻角響應為

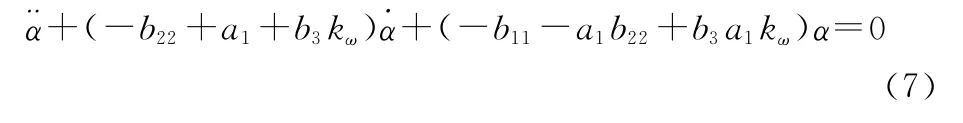
式（7）為一個二階方程，其特征根為

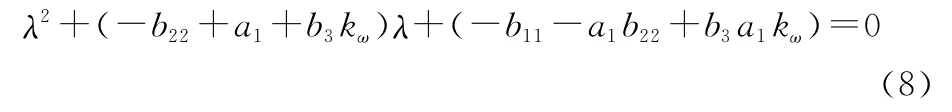
當特征根的解的實部為負數時，姿態角成收斂狀態。上述方程根具有負實部的充要條件是

因為靜穩定彈體本身具有弱阻尼作用，即使在沒有阻尼回路情況下依然可以保證姿態角穩定性，甚至在一定的正反饋情況下依然可以保持穩定性。實際導彈的控制系統中，由于彈體弱阻尼的特性，一般設置kω＞0提高彈體阻尼，獲得更良好的控制性能。當彈體為靜不穩定時，即b11＞0，此時阻尼回路能穩定滿足-a1b22＋b3a1kω＞b11條件的靜不穩定彈體。可以看到，靜不穩定度越大，即b11越大，對應的kω下限值越大，意味著只要反饋增益設計得足夠大，阻尼回路也能穩定靜不穩定彈體姿態，但是實際上kω的取值是有限制的，作為姿態駕駛儀或者過載駕駛儀的內回路，kω的上限值受限于舵機等硬件資源。因此，僅依靠阻尼回路對靜不穩定彈體的穩定范圍極其有限，甚至可能完全無法穩定。

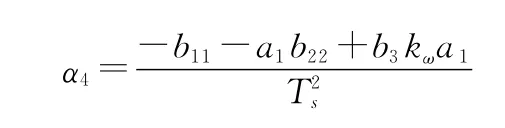
根據勞斯判據可得系統收斂的條件為

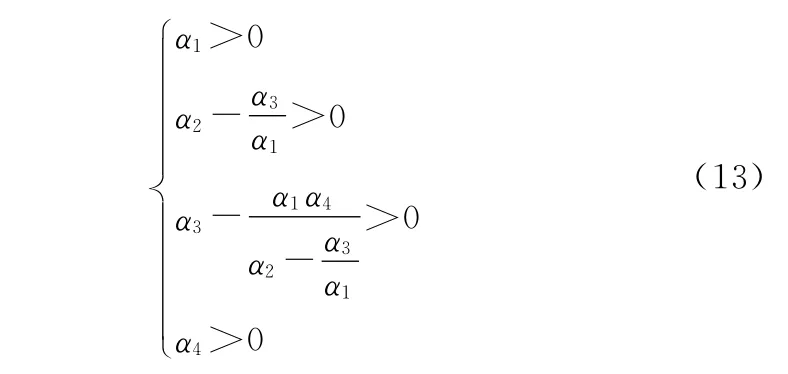
觀察可知，α1＞0和α4＞0兩式一般情況下恒成立，所以決定系統穩定性的是中間兩式。其中，Ts和μs是關于舵機控制參數K P的函數，所以舵機控制參數與阻尼駕駛儀控制參數kω具有一定的關系，具體動態變化關系參見仿真算例。

由于僅依靠阻尼回路控制靜不穩定彈體局限性較大，其所能控制的彈體最大靜不穩定度與等效舵機的帶寬成正比［30］，工程上多采用過載回路來改善彈體特性，這里以兩回路過載駕駛儀為例分析，其組成框圖如圖2所示。

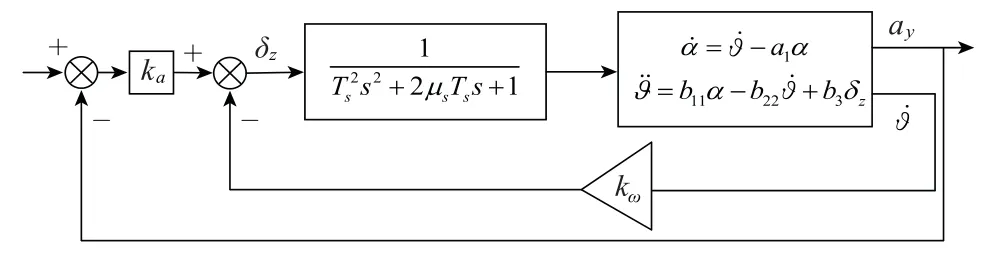
圖2 非旋轉彈兩回路過載駕駛儀結構圖Fig.2 Structure of non-spinning missile two-loop autopilot

在近似條件b22≈0下，可以計算得到兩回路過載駕駛儀作用下彈體自振頻率和阻尼為

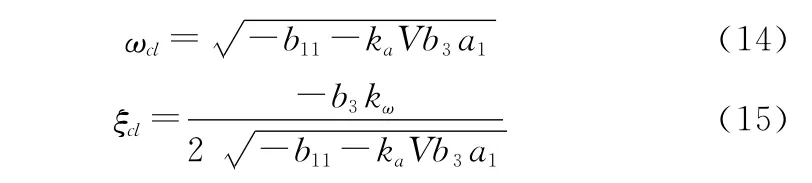
3 旋轉彈阻尼駕駛儀穩定性

旋轉彈阻尼駕駛儀框圖如圖3所示。

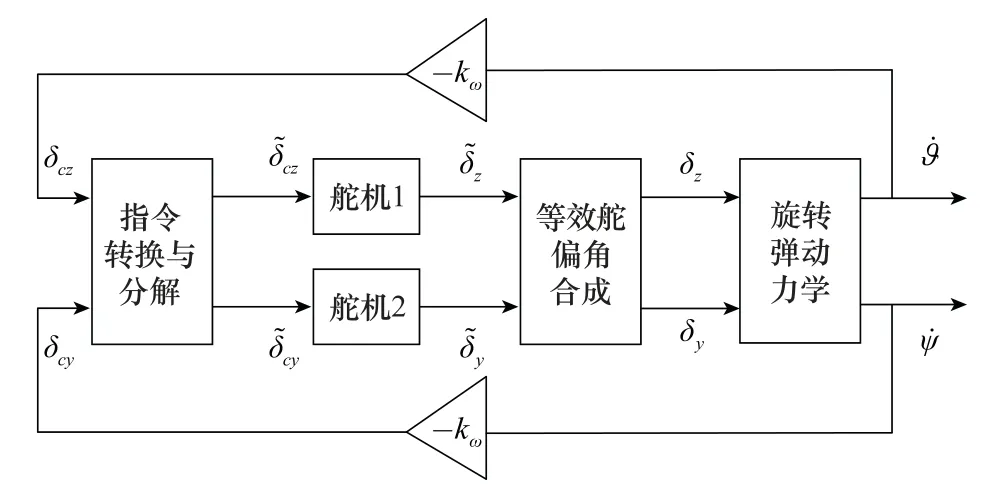
圖3 旋轉彈阻尼回路結構圖Fig.3 Structure of spinning missile damping circuit

當僅考慮舵機系統的穩態響應時，指令到舵偏角的響應是一個簡單的初等矩陣，與舵機的控制參數以及轉速相關。定義復舵偏角δ＝δy＋iδz，復攻角ξ＝β＋iα，復姿態角速度，根據旋轉彈阻尼駕駛儀框圖3可得

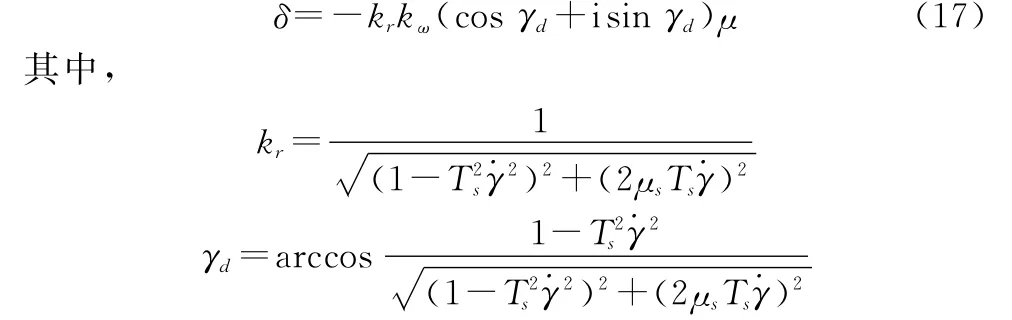
將式（17）代入旋轉彈動力學方程中，并將其寫成復姿態角形式可得

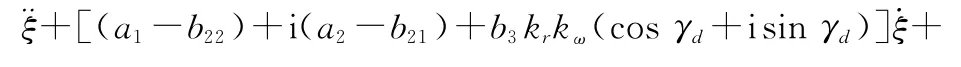
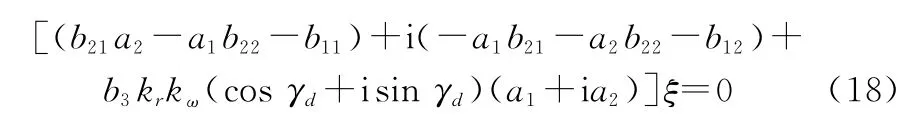
參照相關文獻［32］可得二階復系數微分方程的穩定性條件為

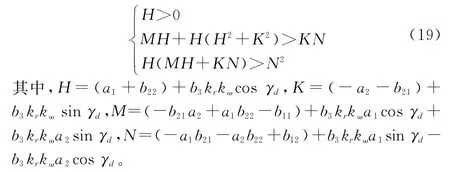
當考慮舵機系統的動態響應時，指令到舵偏角的響應不再是一個簡單的初等矩陣，而是存在一個二階響應環節，系統階次將變為8階，采用復姿態角方法可以降階為4階，根據卡爾丹定理，存在穩定性判據的解析表達式［29］，但是從解析表達式中難以看出各項參數對穩定區域的影響，為使用成熟的線性矩陣不等式求解工具包，本節采用Lyapunov穩定性判據。將式（16）代入式（1）中，并選取狀態變量為則系統的狀態空間方程為

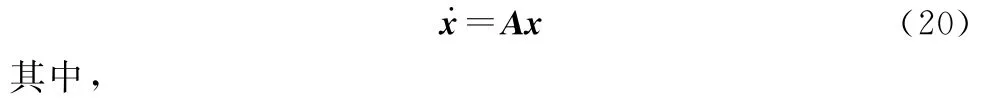
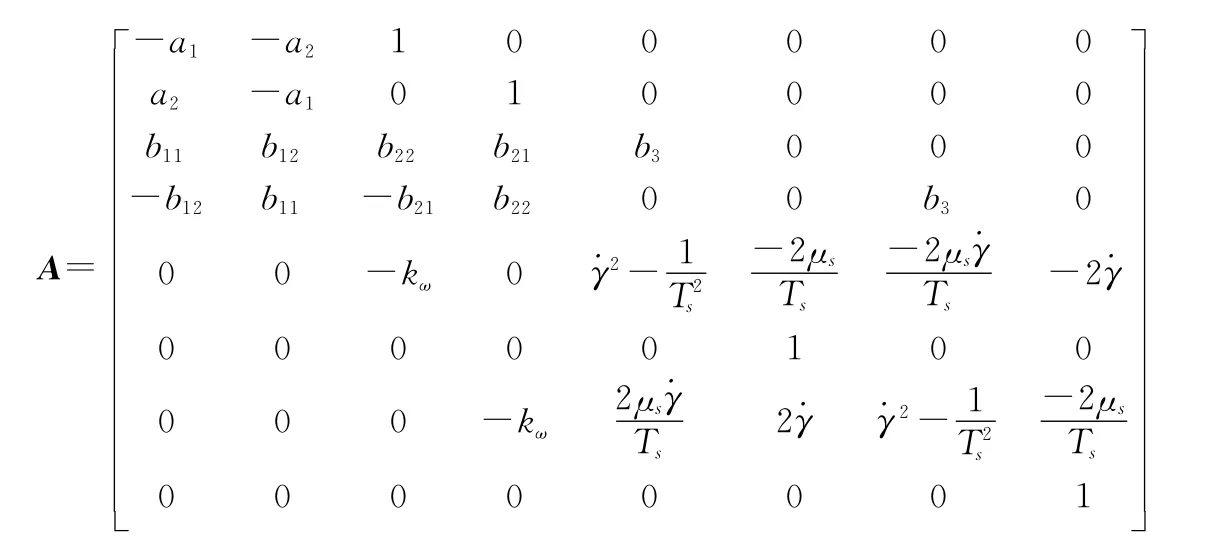
根據李雅普諾夫穩定性理論，上述系統穩定當且僅當A的所有特征值的實部為負數。為了考察上述系統的穩定性，考慮李雅普諾夫方程

系統穩定的充要條件是存在一個正定矩陣M使得

當存在正定矩陣M使得式（22）成立時，計算可以得到，所以系統穩定。針對每一組舵機控制參數以及阻尼反饋增益，可以通過求解線性矩陣不等式（22）的可行性從而判別系統穩定性。舵機的動態響應對阻尼反饋增益的影響參見仿真案例。

4 仿真驗證

本節將進行上述穩定性條件的驗證，給出仿真所需數據，如表2和表3所示，其中對于非旋轉彈，˙γ為零，并且馬格努斯力和力矩以及慣性力矩參數項均為零。

表2 舵機仿真參數表Table 2 Actuator parameters used in the simulation

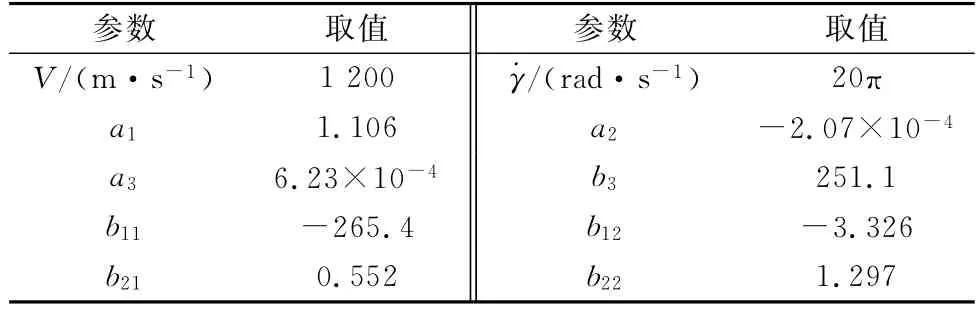
表3 仿真中某旋轉彈飛行參數表Table 3 Spinning missile flight parameters used in the simulation

首先對非旋轉彈進行仿真，給出舵機動態和穩態響應下控制參數穩定域的對比，如圖4所示。

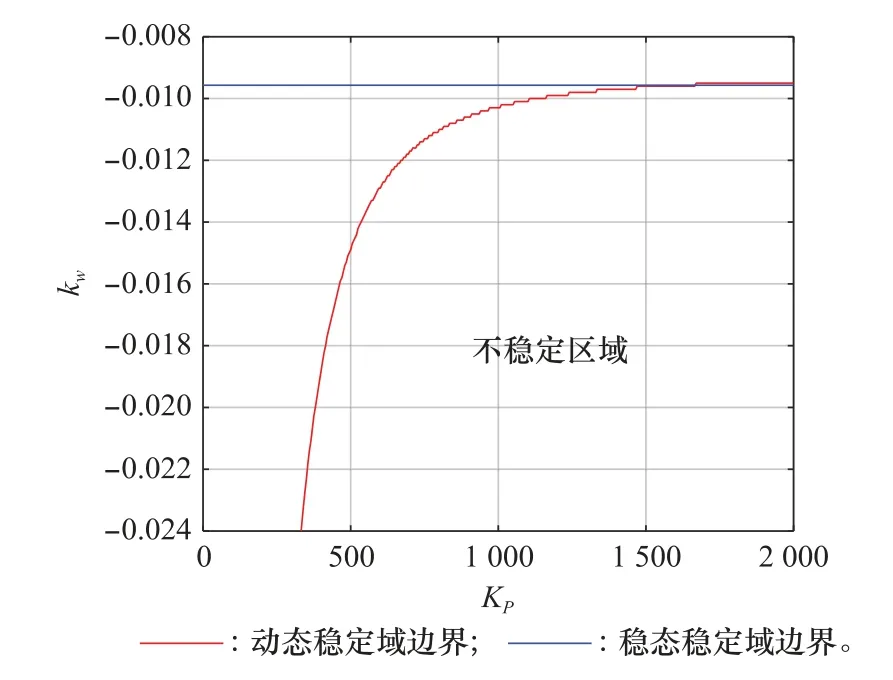
圖4 靜穩定非旋轉彈阻尼參數穩定域Fig.4 Parameter stability region of damping parameters for statically stable non-spinning missile

通過計算分析可知，當忽略彈體舵偏升力的影響時可得穩定邊界條件為kω＞-0.009-569-89，而考慮彈體舵偏升力的影響時可得穩定邊界條件為kω＞-0.009-569-83，對比可知舵面升力項對穩定性邊界影響極小，可以忽略。馬格努斯力項與舵偏升力量級差異不大，因此下面仿真分析中均忽略慮馬格努斯力和舵面升力的影響。考慮舵機的動態響應時，參數K P與kω的穩定域如圖4所示。隨著舵機控制參數的增大，考慮舵機動態與穩態響應下的阻尼駕駛儀參數穩定域趨于相同，即舵機的比例控制參數越大，其響應時間T s越小，舵機的動態響應對彈體運動影響越小。

上例是一個靜穩定的非旋轉彈，現考慮一個靜不穩定的彈體，保持其余參數不變，僅改變b11＝40，可得舵機控制參數與阻尼回路參數穩定域關系如圖5所示。

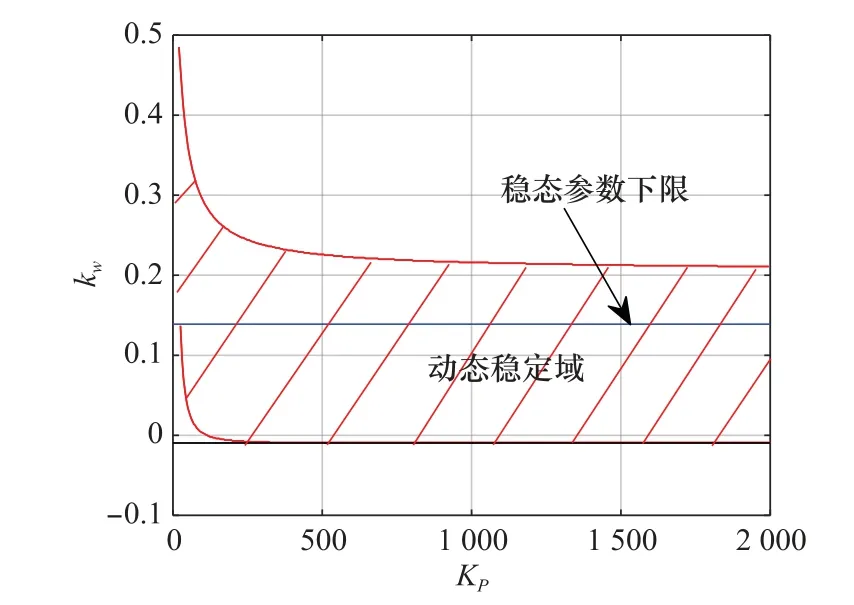
圖5 靜不穩定非旋轉彈阻尼參數穩定域Fig.5 Parameters stability region of damping parameters for statically unstable non-spinning missile

考慮舵機的穩態響應時，阻尼回路的下限分別是-（-b11-a1b22／b3a1）與-（-b22＋a1／b3）項，考慮舵機動態響應情況下，隨著舵機控制參數的增大，阻尼回路參數取值有嚴格的上下界限制。對比可知，僅考慮舵機的穩態響應求得的阻尼回路控制參數很可能會使系統不穩定。因此，靜不穩定的導彈僅依靠阻尼駕駛儀穩定彈體時，應重點考慮舵機的動態響應對其影響。此外，觀察可知考慮舵機動態響應下，靜不穩定的導彈僅依靠阻尼駕駛儀穩定彈體參數穩定區域取值范圍較為有限，這也是工程上較少單獨采用阻尼駕駛儀控制靜不穩定彈體的原因。

旋轉彈阻尼回路反饋參數與舵機參數之間的動態關系如圖6所示。

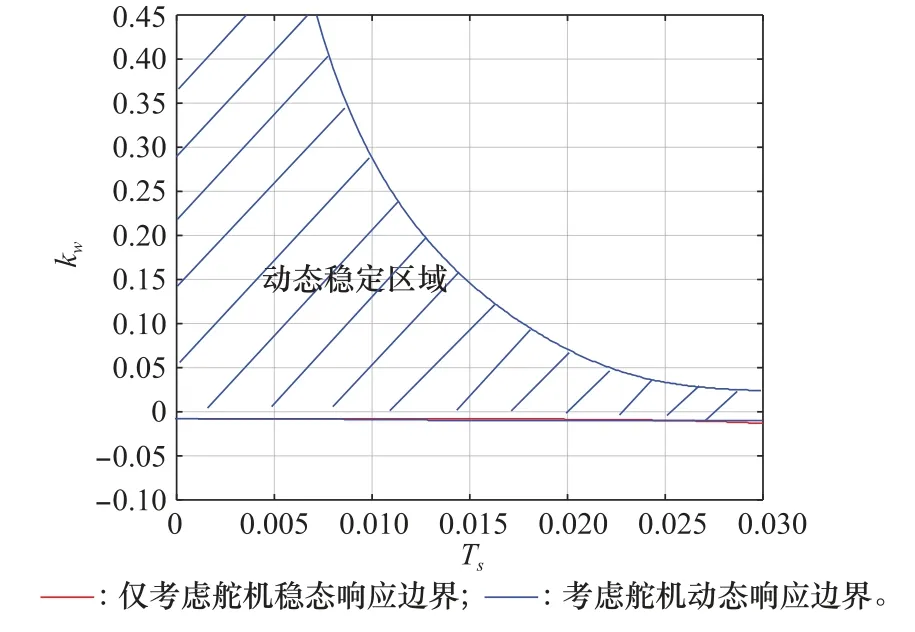
圖6 不同舵機時間常數旋轉彈阻尼參數穩定域Fig.6 Parameters stability region of damping parameters of spinning missile under different actuator time constant

圖6顯示，在彈體靜穩定情況下，僅考慮舵機穩態響應時，kω存在下限值，沒有上限值；當考慮舵機動態響應時，使得系統穩定的kω取值范圍與僅考慮舵機穩態響應時接近，并且舵機時間常數越小，取值范圍越接近，同時kω的取值上限隨著舵機時間常數的增大快速減小。隨著舵機時間常數的減小，舵機響應速度越來越快，舵機的動態響應對彈體的影響也越來越小，表現在圖6中，即舵機時間常數趨于零時，舵機動態和穩態響應下的kω的穩定域趨于相同。

現分析不同靜穩定度旋轉彈的阻尼系數取值范圍。保持其余旋轉彈飛行參數不變，僅改變b11，分析旋轉彈阻尼反饋參數的變化，結果如圖7所示。

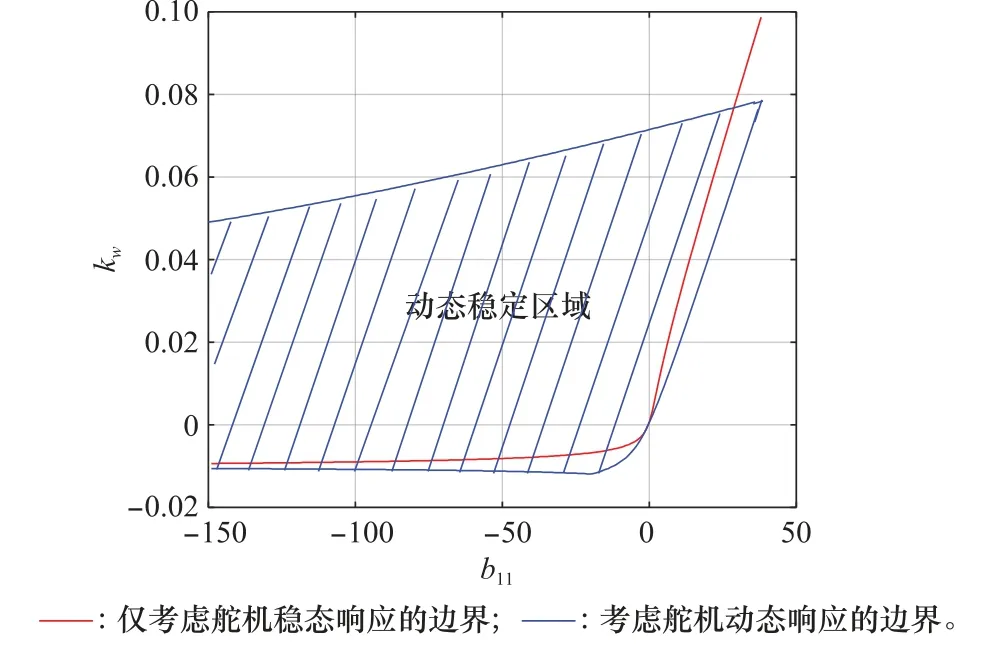
圖7 不同靜穩定度旋轉彈阻尼參數穩定域Fig.7 Parameter stability region of damping parameters for spinning missile with different static stabilities

圖7顯示，僅考慮舵機穩態響應時，當b11＜0，即彈體靜穩定，kω的下限值為負數，且隨著靜穩定度減小，kω下限值緩慢增大，當b11＞0，kω的下限值為正數，且隨著靜不穩定度增大，kω下限值迅速增大，這與非旋轉彈阻尼回路保持一致，同時也與Yan等人［11］的結果相符。當考慮舵機動態響應時，kω的下限值與舵機穩態響應時接近，并且略有增大，但是僅考慮舵機穩態響應時，kω沒有上限值，考慮舵機動態響應時，kω的上限值被嚴格限制，并且隨著靜穩定度減小略微增大，當彈體靜不穩定度到達一定程度時，不存在使得彈體穩定的kω參數。

5 結 論

本文應用勞斯判據推導了非旋轉彈阻尼回路反饋增益的穩定邊界，得出舵機的動態響應使非旋轉彈阻尼反饋增益發生變化，尤其對于靜不穩定彈體，僅考慮舵機的穩態響應求得的阻尼回路控制參數很可能會使系統不穩定。

應用復姿態角方法和Lyapunov穩定性判據推導了旋轉彈反饋增益的穩定邊界，得出舵機的動態響應使旋轉彈阻尼反饋增益穩定區域變小，并且相較于僅考慮舵機的穩態響應，舵機的動態響應下，阻尼反饋參數上限隨著舵機時間常數增大快速減小。