能量開放場地中地層相對位移模型研究

杜修力,周 楠,趙 密,黃景琦,劉鵬程,蘇馳翔

(1.北京工業(yè)大學城市與工程安全減災教育部重點實驗室,北京 100124; 2.北京科技大學土木與資源工程學院,北京 100083)

引言

近年來，隨著我國基礎(chǔ)設(shè)施建設(shè)的快速發(fā)展，大量地下結(jié)構(gòu)工程得到大規(guī)模建設(shè)，如地鐵隧道、地下車站、山嶺隧道等。同時我國又處于歐亞地震帶與環(huán)太平洋地震帶之間，為強地震高發(fā)的國家。因此，在地下結(jié)構(gòu)的運行周期內(nèi)，保證其地震安全性是科學研究及工程設(shè)計的重要問題。

對于地下結(jié)構(gòu)的抗震問題，目前已開展了大量的研究工作[1-4]，而合理且簡便的實用抗震分析方法是這些研究所要達到的最終目標。通過現(xiàn)場觀測、模型試驗和理論分析表明，地下結(jié)構(gòu)的地震響應(yīng)受控于周圍圍巖土體的變形，結(jié)構(gòu)在地震作用下隨周圍巖土體一起振動，其加速度、位移等結(jié)構(gòu)響應(yīng)與周圍巖土體基本一致[5-6]。根據(jù)地下結(jié)構(gòu)的地震響應(yīng)特性，日本學者在20世紀70年代提出了將地層相對位移作為荷載的擬靜力分析方法—反應(yīng)位移法[7-9]。反應(yīng)位移方法計算步驟簡單明確，模型簡單，是一種實用性很強的擬靜力分析方法，在日本的地鐵區(qū)間隧道、地鐵車站和地下停車場等多種地下結(jié)構(gòu)中得到了廣泛應(yīng)用，并寫入日本相關(guān)設(shè)計規(guī)范中，如《大型地下結(jié)構(gòu)抗震設(shè)計指南》等[10]。我國多部規(guī)范也采用了反應(yīng)位移方法作為地下結(jié)構(gòu)地震響應(yīng)分析的分析方法之一，如《城市軌道交通抗震設(shè)計規(guī)范》《城市軌道交通工程設(shè)計規(guī)范》等[11-12]。在反應(yīng)位移方法中，地震荷載包括土層相對位移對結(jié)構(gòu)產(chǎn)生的地震土壓力、結(jié)構(gòu)周圍土層對其的剪切力和結(jié)構(gòu)本身在地震作用下的慣性力。周圍土層對結(jié)構(gòu)的約束作用通過地基彈簧進行模擬。圖1給出了經(jīng)典反應(yīng)位移方法示意。

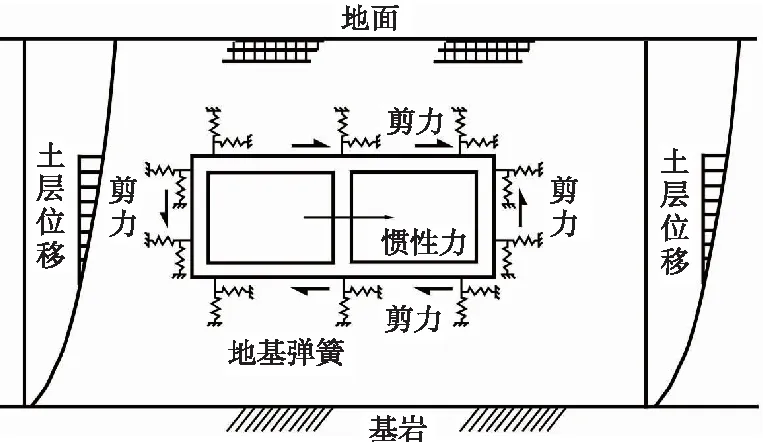
圖1 經(jīng)典反應(yīng)位移方法示意

在反應(yīng)位移方法[13-15]中，地震作用主要通過地震作用下的地層變形實現(xiàn)，地層變形模式的假設(shè)是否合理直接決定了反應(yīng)位移方法的準確性。在日本《大型地下結(jié)構(gòu)抗震設(shè)計指南》中，基于建設(shè)地下結(jié)構(gòu)所在的表層地基反應(yīng)位移為基巖以上土層的一階模態(tài)的假設(shè)，推導出地層位移沿深度方向按余弦函數(shù)分布，給出了基于基巖速度設(shè)計譜的位移分布函數(shù)。我國《城市軌道交通抗震設(shè)計規(guī)范》中同樣假設(shè)地層位移按照余弦函數(shù)分布，但這些位移模型的提出是基于假定設(shè)計地震基準面為剛性基巖面，其上覆土層等效為能量半封閉的系統(tǒng)(即在水平方向上能量開放，但在豎直方向上能量封閉的系統(tǒng))，地震動從基巖面?zhèn)魅胪翆觾?nèi)很難再傳輸出去，基巖以上土層場地響應(yīng)可近似等效為單自由度的一維振動響應(yīng)。這種假設(shè)對于大部分城市的土層場地是合理的，但作為沉積土層，往往在土層底部會遇到波阻抗突然增大的巖石層。隨著城市軌道交通的快速發(fā)展，實際工程中遇到了很多場地條件難以等效為能量半封閉的情況，如金安橋地鐵車站其土層波阻抗沿著深度方向并未出現(xiàn)明顯增大情況；京張高鐵八達嶺車站完全建設(shè)于山體之中等。對于這種情況，很難再將地下結(jié)構(gòu)所在場地的地震響應(yīng)問題等效為能量半封閉的體系，其實際上為一種能量開放體系。對于可等效為能量開放的場地，繼續(xù)使用規(guī)范中給出的余弦函數(shù)的位移分布模式和設(shè)計地震基準面的選取方法進行反應(yīng)位移方法抗震設(shè)計將帶來很大的不合理性。因此，需要針對能量開放場地的位移場響應(yīng)進行系統(tǒng)研究，以提出適用于此類場地的地層位移模型。

本文將水平均勻半空間能量開放系統(tǒng)在地震動垂直入射時的場地響應(yīng)問題等效為應(yīng)力波的一維傳播問題。通過一維土柱模型模擬場地土的動力響應(yīng)特性，模型頂部為自由表面，底部設(shè)置黏性人工邊界，地震動輸入通過等效節(jié)點力的方式進行輸入。模擬不同場地類別、地震烈度等級及近遠場效應(yīng)下場地的位移響應(yīng)，最終提出能量開放體系的一種地層位移模型。

1 能量開放場地的地震響應(yīng)分析模型

對于均勻水平半空間場地，在地震動垂直入射情況下，其地震響應(yīng)可簡單等效為一維土柱模型進行分析。建立的一維土柱模型如圖2所示。

圖2 能量開放場地一維計算模型

考慮輻射阻尼效應(yīng)，在一維土柱模型底部施加黏性邊界，黏性邊界的阻尼系數(shù)為

CT=ρcs

(1)

為實現(xiàn)一維土柱的波動輸入，在桿件底部施加等效節(jié)點力F(t)，則

(2)

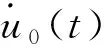
為合理研究不同圍巖等級情況下能量開放場地的地震動響應(yīng)，針對Ⅲ、Ⅳ、Ⅴ級圍巖場地進行分析，各級圍巖基本參數(shù)如表1所示。

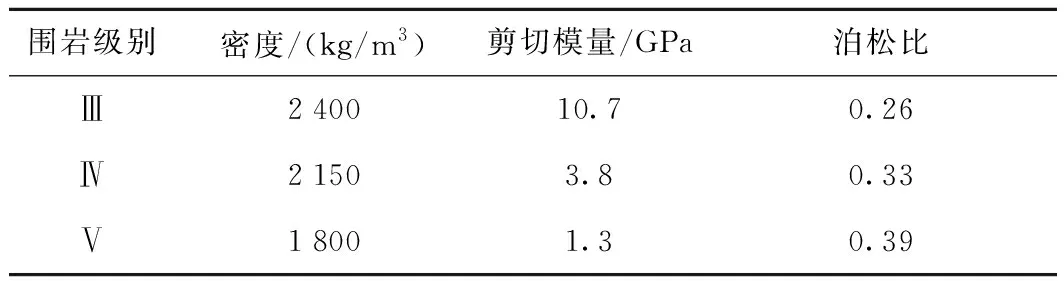
表1 場地材料參數(shù)

2 輸入地震動及模擬工況

地震動為人工合成地震動，選取反應(yīng)譜為GB20909—2014《城市軌道交通結(jié)構(gòu)抗震設(shè)計規(guī)范》中給出的加速度設(shè)計反應(yīng)譜，見圖3。結(jié)構(gòu)阻尼比取ξ=0.05，參數(shù)η和γ分別取1.0。

對于規(guī)范中給出的設(shè)計地震動加速度反應(yīng)譜特征周期Tg，對于同一類場地在3個不同反應(yīng)特征周期分區(qū)(0.35 s區(qū)、0.40 s區(qū)和0.45 s區(qū))具有不同的Tg值。本研究取3個分區(qū)的Tg平均值作為每類場地的特征周期。選取的特征周期Tg見表2。

表2 本研究選取的反應(yīng)譜特征周期Tg s

為描述地震地面運動從開始、強震段、自然衰減的全過程，采用經(jīng)典的非平穩(wěn)模型[16]

F(t)=f(t)A(t)

(3)

式中，f(t)為非平穩(wěn)強度函數(shù)，其函數(shù)形式為

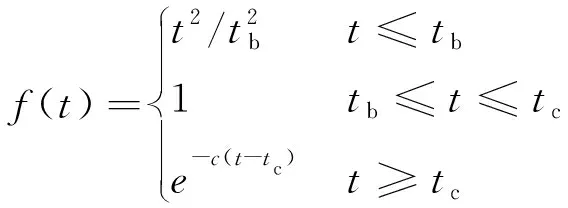
(4)

式中，tb=0.5Ts；tc=1.2Ts；c=2.5/Ts。其中，Ts為平穩(wěn)持時，其取值參照文獻[17]中結(jié)果取值。

圖4給出Ⅳ類場地在設(shè)計烈度為7度情況下，1條人工合成地震動的時程曲線。

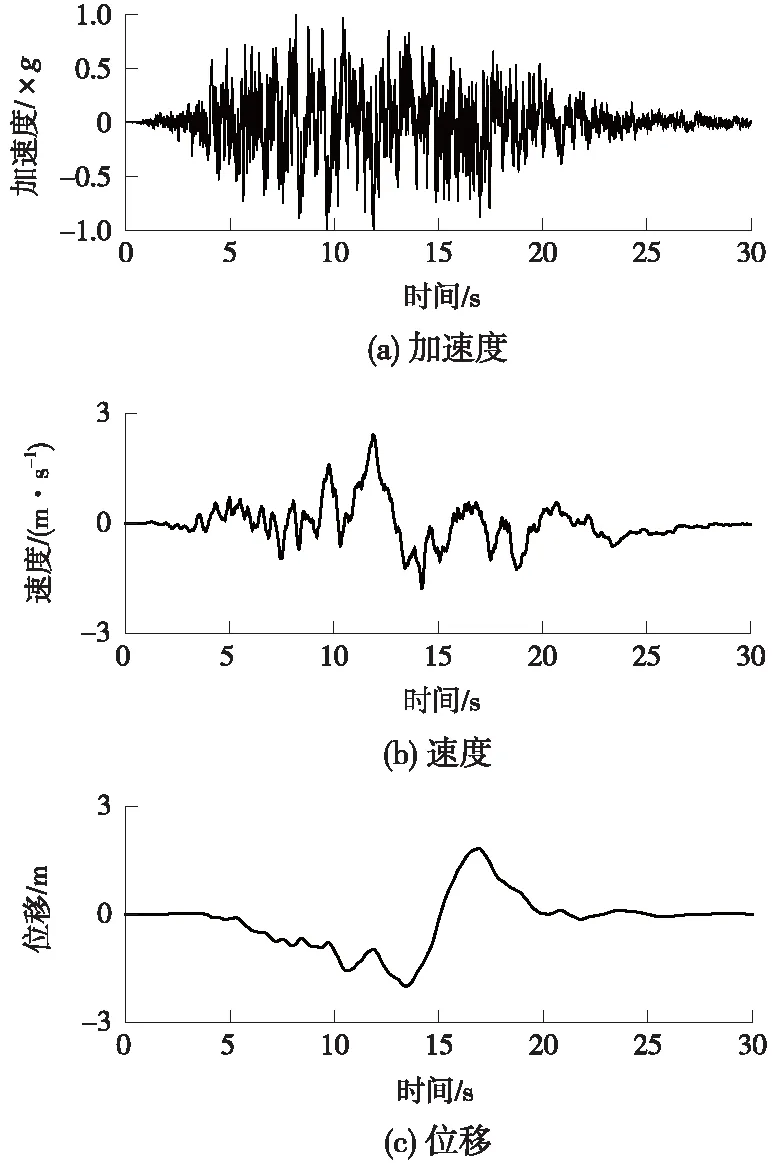
圖4 人工合成地震動時程曲線

3 結(jié)果分析

對于每一類場地條件，抗震設(shè)防烈度分別設(shè)為6度、7度、8度和9度。輸入地震動在合成時區(qū)分近場和遠場的區(qū)別。每個工況共計算90條人工地震動，通過數(shù)理統(tǒng)計的方法獲得不同場地條件及不同設(shè)防烈度下能量開放體系中地層的峰值剪應(yīng)變分布規(guī)律。

3.1 Ⅲ級圍巖條件不同設(shè)防烈度下峰值剪應(yīng)變分布規(guī)律

圖5、圖6分別給出了不同設(shè)防烈度下，Ⅲ級圍巖場地的峰值剪應(yīng)變隨埋深的分布規(guī)律。從圖5、圖6中可以看出，隨著深度增加，在各級設(shè)防烈度下的峰值剪應(yīng)變均先增加后減小，直到基本保持不變，并且在各級設(shè)防烈度下，峰值剪應(yīng)變的拐點深度位置大致相同。同時，設(shè)防烈度的增加會使得峰值剪應(yīng)變增大，衰減至平穩(wěn)狀態(tài)的深度值更大。在同一設(shè)防烈度下，近場地震動引起的最大剪應(yīng)變要略大于遠場地震動引起的峰值剪應(yīng)變。

圖5 不同設(shè)防烈度下峰值剪應(yīng)變分布規(guī)律

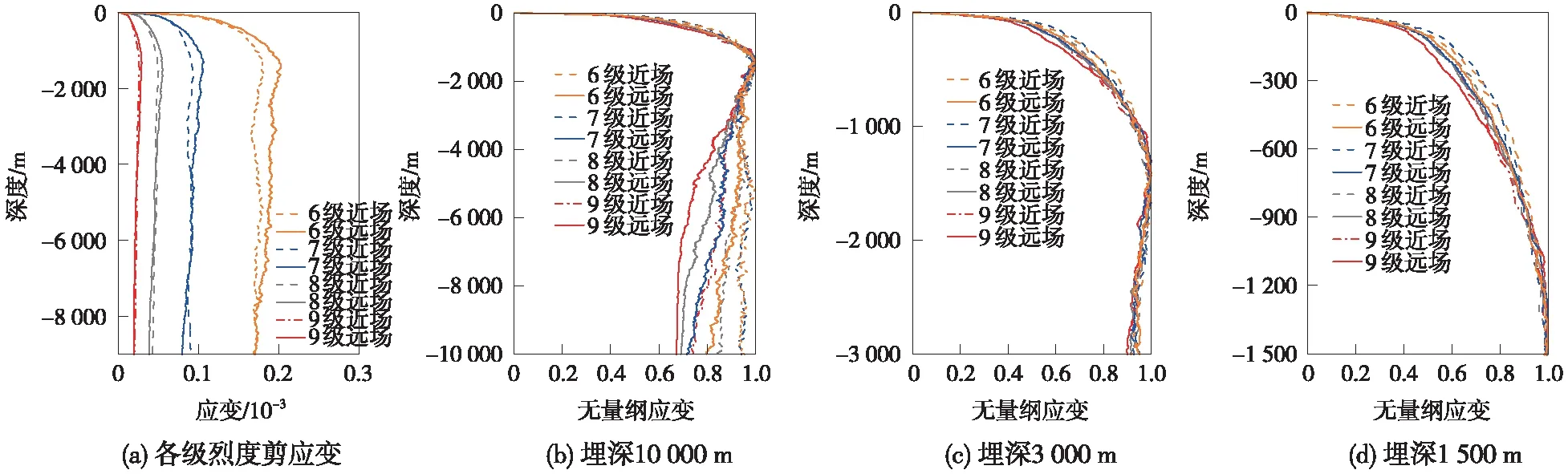
圖6 各級設(shè)防烈度下峰值剪應(yīng)變及無量綱化峰值剪應(yīng)變

3.2 Ⅳ級圍巖條件不同設(shè)防烈度下峰值剪應(yīng)變分布規(guī)律

圖7、圖8分別給出了不同設(shè)防烈度下，Ⅳ級圍巖場地的峰值剪應(yīng)變隨深度變化的分布規(guī)律。從圖7、圖8中可以看出，不同設(shè)防烈度情況下的峰值剪應(yīng)變均隨埋深增加呈先增大后減小趨勢，直到基本保持不變。各設(shè)防烈度情況下，峰值剪應(yīng)變的拐點埋深大致相同。同時，設(shè)防烈度的增加會使得峰值剪應(yīng)變增大，衰減至平穩(wěn)狀態(tài)的深度值增加。在同一設(shè)防烈度下，近場地震動引起的最大剪應(yīng)變要略大于遠場地震動引起的峰值剪應(yīng)變。

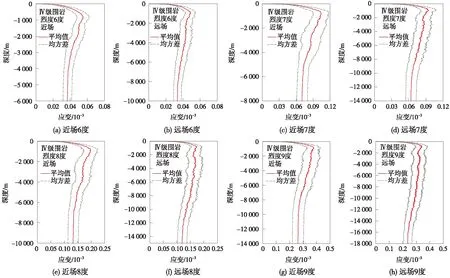
圖7 不同設(shè)防烈度下峰值剪應(yīng)變分布規(guī)律

圖8 各級設(shè)防烈度下峰值剪應(yīng)變及無量綱化峰值剪應(yīng)變

3.3 Ⅴ級圍巖條件下不同設(shè)防烈度下峰值剪應(yīng)變分布規(guī)律

圖9、圖10分別給出了不同設(shè)防烈度下，Ⅴ級圍巖場地的峰值剪應(yīng)變隨深度變化的分布規(guī)律。從圖9、圖10中可以看到，隨著深度增加，不同設(shè)防烈度情況下峰值剪應(yīng)變的變化規(guī)律均先增加后減小，直到基本保持不變。各設(shè)防烈度情況下，峰值剪應(yīng)變的拐點埋深大致相同。同時，設(shè)防烈度的增加會使得峰值剪應(yīng)變增大，衰減至平穩(wěn)狀態(tài)的深度值增加。在同一設(shè)防烈度下，近場地震動引起的最大剪應(yīng)變要略大于遠場地震動引起的峰值剪應(yīng)變。

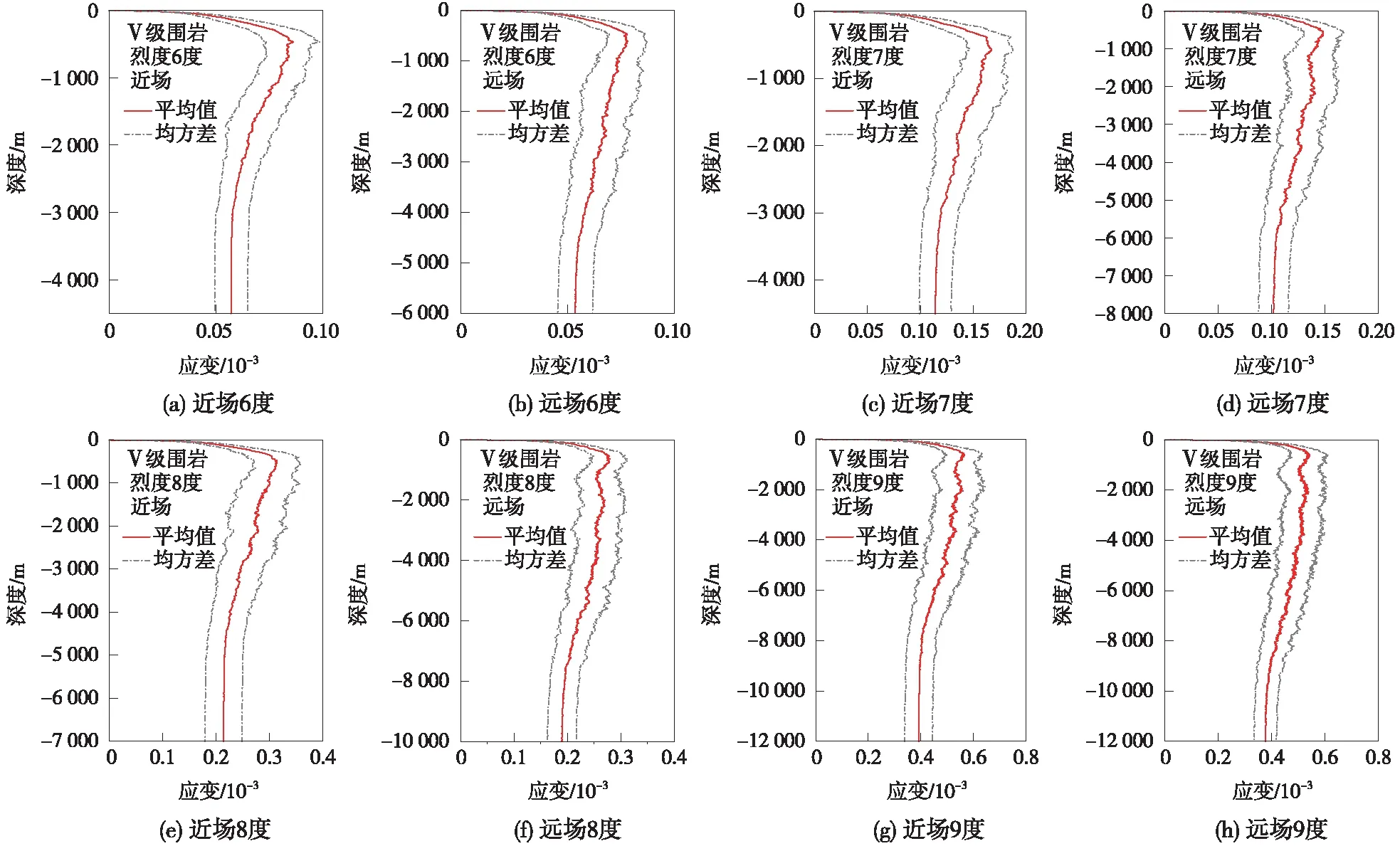
圖9 不同設(shè)防烈度下峰值剪應(yīng)變分布規(guī)律

圖10 各級設(shè)防烈度下峰值剪應(yīng)變及無量綱化峰值剪應(yīng)變

3.4 不同圍巖級別轉(zhuǎn)折深度值對比

圖11給出了無量綱化后的剪應(yīng)變在不同場地條件及不同設(shè)防烈度下轉(zhuǎn)折深度值規(guī)律。從圖11中可以看出，在同一抗震設(shè)防烈度條件下，不同圍巖場地的轉(zhuǎn)折深度和下降斜率基本一致。因此，可以用一個統(tǒng)一公式對不同場地條件及不同設(shè)防烈度下的峰值剪應(yīng)變進行描述。

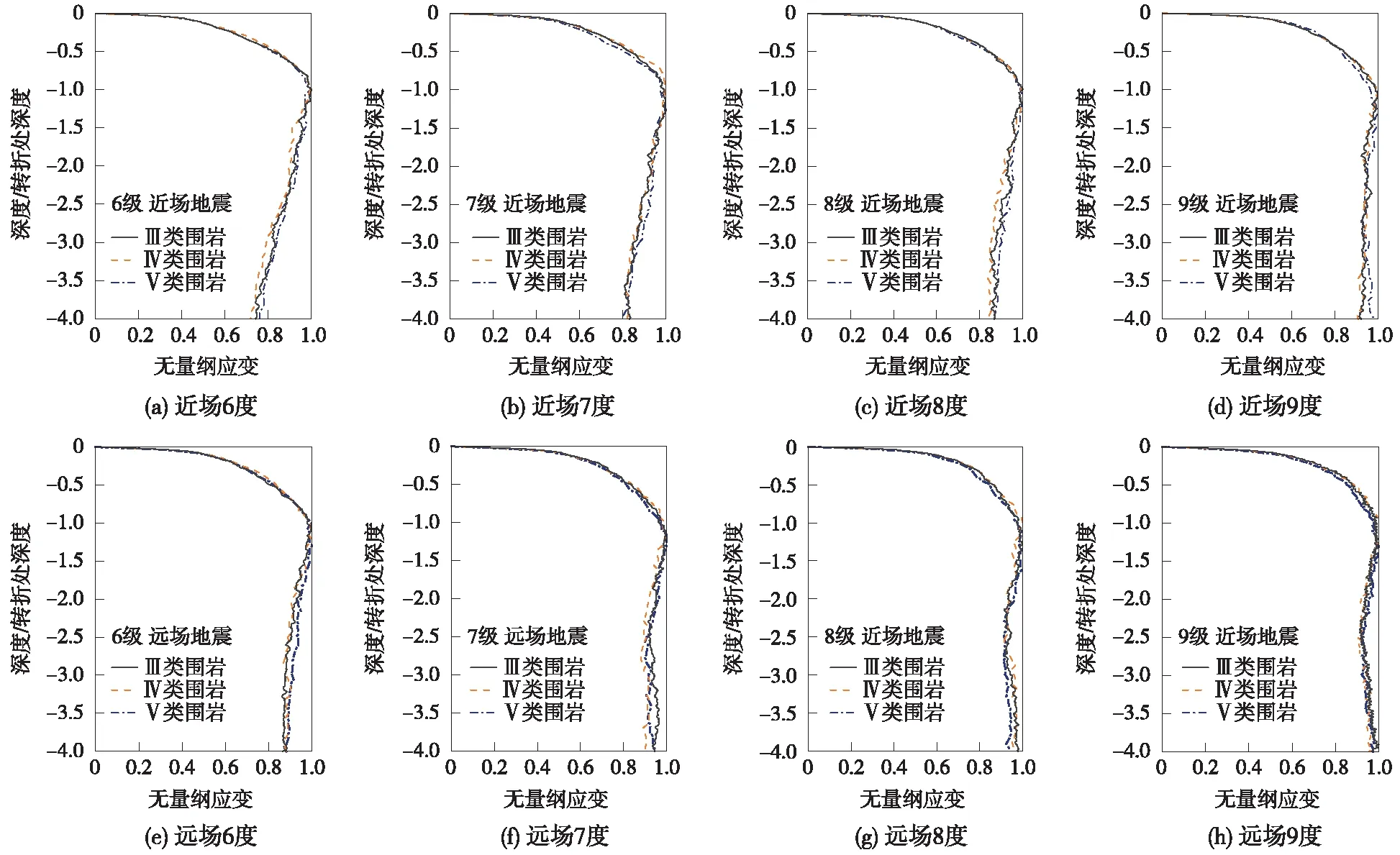
圖11 不同場地條件及不同設(shè)防烈度下轉(zhuǎn)折深度值規(guī)律

3.5 參數(shù)擬合

針對剪應(yīng)變隨深度與轉(zhuǎn)折深度比值的變化規(guī)律進行參數(shù)擬合，得到擬合公式

(5)

式中，γ為剪應(yīng)變；H為埋深；γmax為埋深各點最大剪應(yīng)變，其值見表3；Hl為應(yīng)變沿深度方向增減拐點深度，其值見表4；κ為圖12中峰值點后直線斜率，其值見表5。

表3 γmax取值 ×10-3

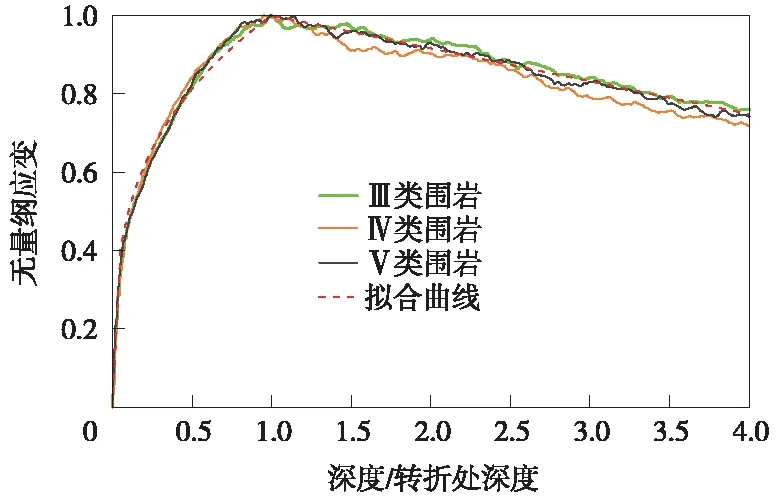
圖12 剪應(yīng)變隨深度與轉(zhuǎn)折深度比值變化規(guī)律

表4 拐點埋深Hl m

表5 斜率κ

式(5)能很好地反映在不同場地條件及不同設(shè)防烈度下，峰值剪應(yīng)變隨深度與轉(zhuǎn)折深度比值的變化規(guī)律，擬合曲線如圖12所示。

4 結(jié)論

針對均勻半空間能量開放場地的圍巖地震動響應(yīng)規(guī)律進行了研究，分析了不同場地條件及不同設(shè)防烈度下峰值剪應(yīng)變分布規(guī)律，并對其轉(zhuǎn)折深度值的規(guī)律進行了進一步分析。研究考慮了場地類別、設(shè)防烈度和近、遠場效應(yīng)等影響，主要結(jié)論如下。

(1)在能量開放的場地中，其地層剪應(yīng)變模式并非按照余弦函數(shù)的形式分布。

(2)研究提出不同場地條件及不同設(shè)防烈度下峰值剪應(yīng)變分布規(guī)律。模擬結(jié)果表明，在均勻半空間能量開放場地圍巖的地震動響應(yīng)隨著深度的增加先增大后減小，最后趨于平均。在同一場地條件下，地震峰值加速度越大地震動響應(yīng)越大。在同一地震峰值加速度條件下，場地類別越好則圍巖的地震動響應(yīng)越小。

(3)研究提出不同場地條件及不同設(shè)防烈度下剪應(yīng)變隨深度與轉(zhuǎn)折深度比值的變化規(guī)律，在同一抗震設(shè)防烈度條件下，不同圍巖場地的轉(zhuǎn)折深度和下降斜率基本一致，同時根據(jù)模擬結(jié)果對其進行參數(shù)擬合。研究發(fā)現(xiàn)，在Ⅴ類圍巖場地條件時，拐點深度為500 m；在Ⅳ類圍巖場地條件時，拐點深度為850 m；在Ⅲ類圍巖場地條件時，拐點深度為1 500 m。