45 t軸重重載鐵路扣件系統(tǒng)剛度分析

薄棟乾,韋 凱,宋卓西,郭恭兵,王 顯

(1.西南交通大學高速鐵路線路工程教育部重點實驗室,成都 610031； 2.西南交通大學土木工程學院,成都 610031)

引言

隨著科技水平不斷提高，重載鐵路向大軸重、長編組和大牽引總重的運輸方式發(fā)展，而提高軸重是重載列車降低運行成本最有效的措施[1]。目前，在重載鐵路發(fā)達國家，如美國、澳大利亞等已開行36～40 t軸重重載列車[2]，未來重載列車軸重仍有進一步提高的趨勢。

隨著列車軸重不斷提高，扣件系統(tǒng)剛度隨之進行不斷調整[3-6]。王琪[7]通過對比分析27 t與25 t軸重對軌道結構的受力影響，對扣件系統(tǒng)適應性進行了分析并提出相應的強化對策；徐浩等[8]建立了重載貨車-無砟軌道-橋梁耦合動力學模型，研究32.5 t軸重重載鐵路橋上長枕埋入式無砟軌道扣件系統(tǒng)參數；許良善[9]通過建立車輛-軌道動力學模型及進行有砟軌道實尺模型試驗，對35～40 t軸重重載鐵路軌道強度進行了研究；楊吉忠等[10]分別使用車輛-軌道耦合動力學理論及基于顯式有限元方法的輪軌瞬態(tài)滾動接觸理論分析模型，計算不同頻率下的軌道動態(tài)響應，提出了40 t軸重重載鐵路扣件的最優(yōu)動態(tài)剛度范圍。

綜上，國內對于25 t軸重重載鐵路扣件系統(tǒng)剛度設計已有較為成熟的設計經驗，對于35～40 t軸重重載鐵路也開展了一定研究，但針對更高軸重(如45 t)的研究較少。而目前已開始對澳大利亞等國家出口45 t軸重列車[11-12]，如扣件系統(tǒng)剛度不能適應該高軸重，將對軌道結構造成疲勞傷損等不良影響，從而嚴重影響重載鐵路運輸效率，因此，有必要對45 t軸重重載線路扣件系統(tǒng)剛度展開相關研究。基于45 t軸重重載鐵路，首先通過鋼軌容許應力法及軌道容許變形法對扣件系統(tǒng)靜剛度范圍進行合理分析；然后建立重載貨車-有砟軌道空間耦合動力學模型，計算不同輪軌激擾、不同剛度條件下車軌耦合系統(tǒng)的動力響應，從而分析扣件系統(tǒng)合理動剛度范圍。研究成果可供大軸重重載鐵路扣件系統(tǒng)剛度設計參考。

1 扣件系統(tǒng)靜剛度分析

1.1 鋼軌容許應力法

由強度設計準則，鋼軌在重載列車作用下產生的彎曲應力應小于其容許應力，容許應力法即通過鋼軌容許應力計算扣件系統(tǒng)靜剛度。

鋼軌容許應力與鋼軌支座剛度關系[13]如下

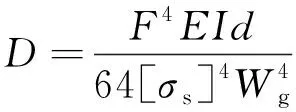
(1)

式中，D為鋼軌支座剛度；F為集中荷載；Wg為鋼軌下部斷面系數；EI為鋼軌抗彎剛度；[σs]為鋼軌容許應力；d為軌枕間距。

(2)

式中，σs為鋼軌屈服極限；K為安全系數。

有砟軌道鋼軌支座剛度D由扣件系統(tǒng)靜剛度D1、有砟道床剛度D2及路基剛度D3串聯(lián)而來，即

(3)

則扣件系統(tǒng)靜剛度與鋼軌容許應力關系為

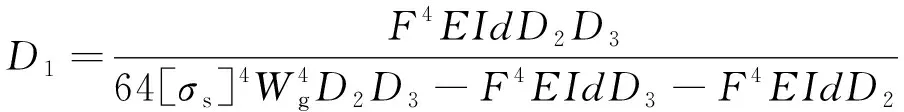
(4)

相關計算參數如表1所示[14]。

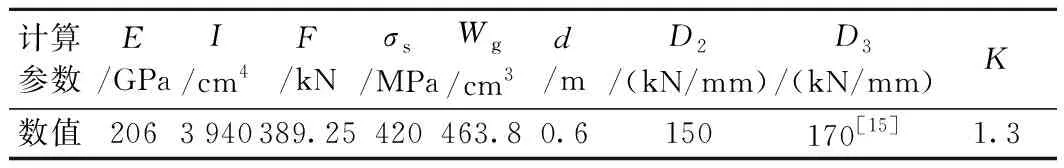
表1 扣件系統(tǒng)靜剛度計算參數

經計算，扣件系統(tǒng)靜剛度為36.1 kN/mm。重載列車作用下鋼軌彎曲應力遠小于鋼軌容許應力，因此，該計算得到的剛度值為扣件系統(tǒng)靜剛度最小值。

1.2 軌道允許變形法

軌道在重載列車垂向荷載作用下會產生下沉變形，其計算公式為

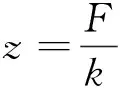
(5)

式中，z為鋼軌下沉位移；F為集中荷載；k為軌道整體剛度。

鋼軌下沉位移較小時，軌道承受列車荷載較大，會加快軌道部件的傷損；軌道下沉位移較大時，會使軌下基礎累積塑性變形加大，增加維修工作量，因此，鋼軌下沉位移存在一個合理范圍。參考國內外重載鐵路有砟軌道鋼軌下沉位移限值，45 t軸重重載鐵路線鋼軌下沉位移的允許范圍為2.5～3.3 mm。

而鋼軌支座剛度D與軌道整體剛度k的關系如下

(6)

式中各項參數含義同式(1)。聯(lián)立式(4)～式(6)，則可得鋼軌下沉位移與扣件系統(tǒng)靜剛度的關系如下

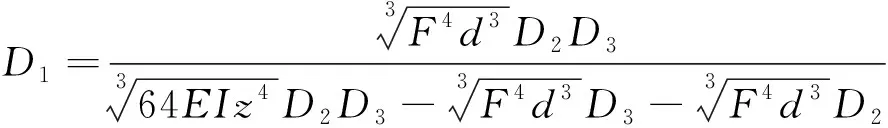
(7)

鑒于有砟道床剛度隨時間、密實程度變化會發(fā)生改變，為保證在不同道床剛度下鋼軌下沉位移均能滿足設定的位移范圍，參考實測道床穩(wěn)定區(qū)的道床剛度，通過式(7)計算不同道床剛度及扣件系統(tǒng)靜剛度條件下的鋼軌下沉位移，如圖1所示。其中，扣件系統(tǒng)靜剛度取值范圍為80～800 kN/mm，道床剛度取值為80～170 kN/mm。

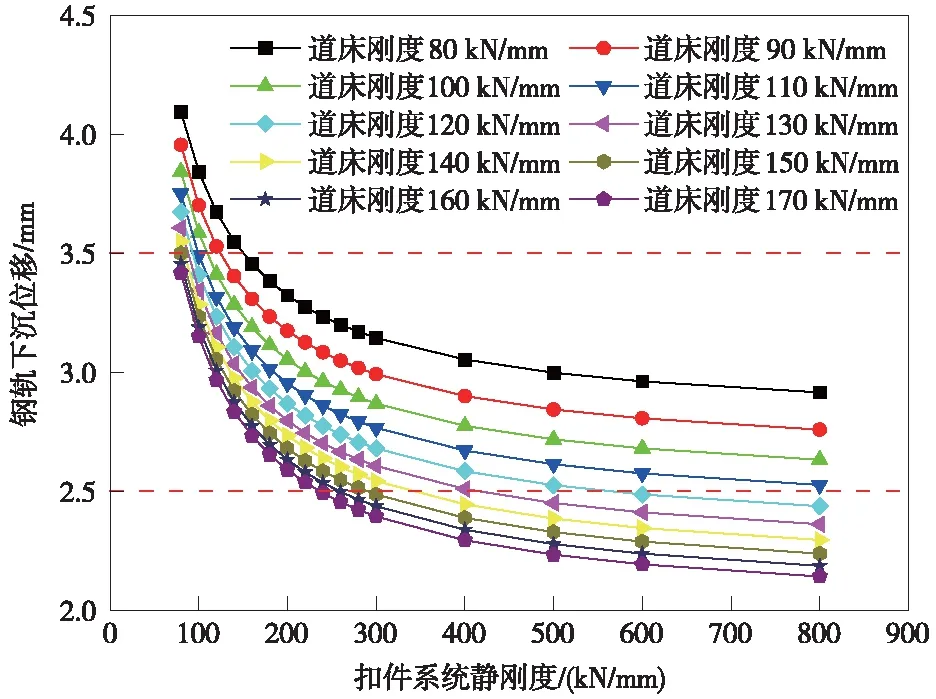
圖1 不同扣件系統(tǒng)靜剛度下鋼軌下沉位移曲線

由圖1可知，道床剛度一定時，隨著扣件系統(tǒng)靜剛度增大，鋼軌下沉位移不斷降低，且下降趨勢逐漸變緩。以道床剛度處于120 kN/mm時為例，當扣件剛度從80 kN/mm增加至200 kN/mm，鋼軌下沉位移從3.67 mm降低至2.87 mm，減少0.80 mm；而當扣件剛度從200 kN/ mm增加至800 kN/ mm，鋼軌下沉位移從2.87 mm降低至2.44 mm，僅減小0.43 mm，表明當扣件系統(tǒng)靜剛度處于80～200 kN/mm范圍時，鋼軌下沉位移受其影響波動較大。

為使鋼軌下沉位移處于2.5～3.5 mm設定范圍內，且使其處于穩(wěn)定狀態(tài)，建議扣件系統(tǒng)靜剛度范圍為200～240 kN/mm。

綜合鋼軌容許應力法及軌道容許變形法，45 t軸重重載有砟軌道扣件系統(tǒng)靜剛度應處于200～240 kN/mm范圍內。

2 扣件系統(tǒng)動剛度分析

由于扣件系統(tǒng)墊板自身高分子特性，其靜態(tài)力學性能與動態(tài)力學性能呈現(xiàn)明顯差異性[17]。因此，通過建立車輛-軌道空間耦合動力學模型，獲取不同輪軌系統(tǒng)激擾下、不同扣件剛度條件下45t軸重貨車運營時的動力響應，進而分析扣件系統(tǒng)動剛度的合理取值范圍。

2.1 車輛-軌道耦合動力學模型

圖2為建立的重載貨車-有砟軌道空間耦合動力學模型。貨車模型由單個車體、2個搖枕、4個側架及4個輪對構成，車體及輪對考慮橫移、沉浮、側滾、點頭及搖頭5個運動自由度，搖枕僅考慮搖頭運動自由度，側架考慮橫移、沉浮、點頭及搖頭4個運動自由度。

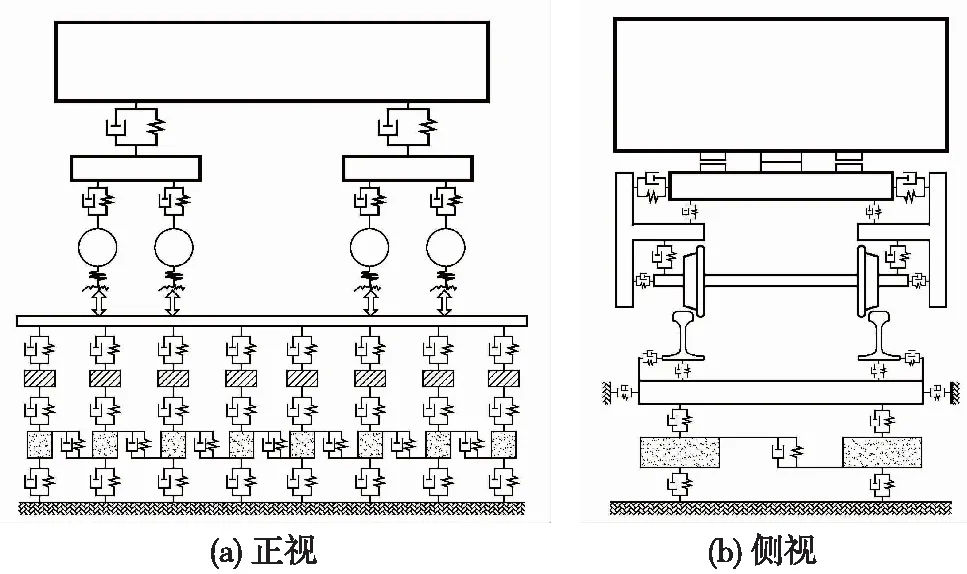
圖2 重載貨車-有砟軌道空間耦合動力學模型

有砟軌道模型由鋼軌、軌枕、有砟道床及路基構成，左右兩股鋼軌均視為連續(xù)彈性離散點支承基礎上的Timoshenko梁，考慮垂向、橫向及扭轉自由度；軌枕視為剛體，考慮垂向、橫向及轉動運動自由度；道床視為剛性質量塊，僅考慮垂向運動自由度[18]。

車軌耦合模型中，輪軌接觸模型的合理選擇對計算結果存在較大影響，本次計算中，應用Hertz非線性彈性接觸理論確定輪軌間法向作用力；輪軌間蠕滑力首先按Kalker線性理論計算，然后進行非線性修正。

2.2 輪軌激勵及評價指標

輪軌系統(tǒng)激擾是引起車輛-軌道耦合系統(tǒng)振動的根本原因，在重載鐵路中，最主要的是軌道不平順及鋼軌焊縫不平順[19-20]。分別以美國五級譜及鋼軌焊縫不平順作為激勵，研究貨車運行速度為90 km/h，扣件剛度在60～600 kN/mm范圍變化時輪軌動態(tài)響應變化規(guī)律，從而提出45 t軸重重載鐵路扣件系統(tǒng)動剛度合理范圍。

(1)美國五級譜

對于重載鐵路，采用美國五級譜作為耦合系統(tǒng)的軌道不平順輸入，波長范圍取1～30 m，其時域隨機不平順樣本沿線路里程分布如圖3所示。

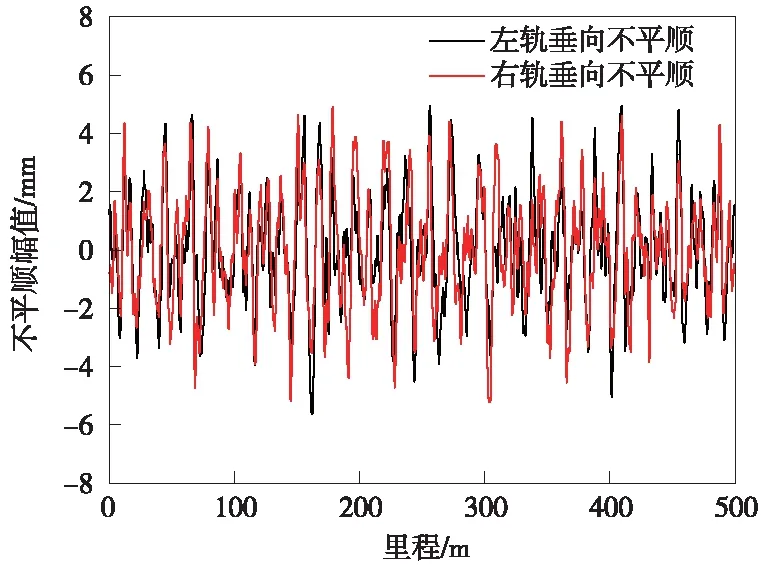
圖3 美國五級譜樣本

(2)焊縫凹陷不平順

焊縫凹陷不平順如圖4所示，分為焊縫處和軟著區(qū)兩部分，可采用組合余弦模型描述。

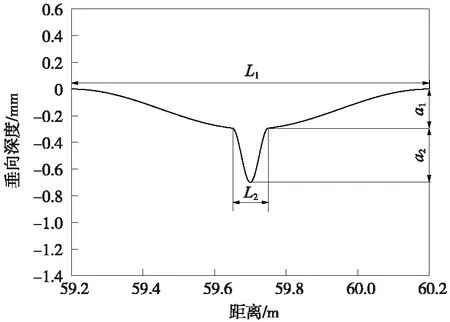
圖4 焊縫凹陷不平順

當0≤x≤(L1-L2)/2，(L1+L2)/2≤x≤L1時

當(L1-L2)/2≤x≤(L1+L2)/2時

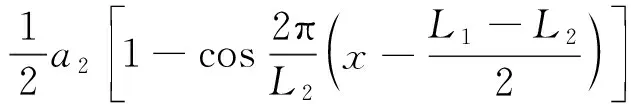
(8)

式中，Z0(x)為焊縫凹陷不平順值；a1為長波波深；a2為短波波深；L1為長波波長；L2為短波波長；x為車輛運行距離。考慮最不利情況，a1取0.3 mm，a2取0.4 mm，L1取1 m，L2取0.1 m。

(3)評價指標

重載貨車動力響應采用輪重減載率評價，其值不應大于0.8；有砟軌道動力響應采用輪軌垂向力、鋼軌垂向位移及枕上壓力評價，其中，鋼軌垂向位移不應超過3.3 mm，枕上壓力不應超過196.0 kN[21]。

2.3 動力響應分析

(1)美國五級譜

圖5給出了美國五級譜激勵下，不同扣件系統(tǒng)動剛度下的車軌耦合系統(tǒng)各項動力響應，由于各剛度下響應曲線非常相似，圖中只給出了60，300，600 kN/mm剛度下的動力響應曲線。

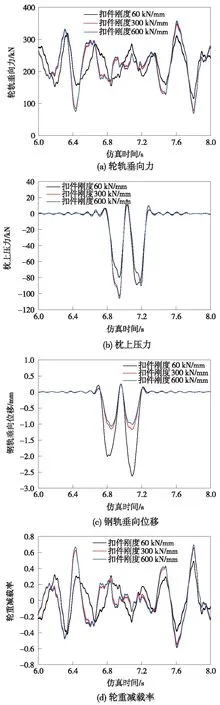
圖5 美國五級譜激勵下輪軌動力響應

由圖5可知，在美國五級譜激勵下，除鋼軌垂向位移隨扣件系統(tǒng)動剛度增大而減小外，其他3個指標均隨剛度增大而增大。這是因為扣件系統(tǒng)剛度越大，簧下質量引起的動態(tài)應力越大，而軌道變形越小。

隨著扣件系統(tǒng)動剛度由60 kN/mm增加至600 kN/mm，輪軌垂向力最大值由331.0 kN增大至361.8 kN，增長9.3%；枕上壓力最大值由89.1 kN增大至106.0 kN，增長19.0%；鋼軌垂向位移最大值由2.62 mm減小至1.07 mm，減少59.2%；輪重減載率最大值由0.49增大至0.7，增長42.9%，可見扣件系統(tǒng)動剛度對美國五級譜引起的輪軌沖擊力、枕上壓力影響較小，而對鋼軌垂向位移、輪重減載率影響較大。

(2)最大動力響應匯總

因鋼軌焊縫不平順動力響應曲線與美國五級譜相似，在此僅繪制4種指標最大值在不同扣件剛度作用下的變化曲線，如圖6所示。

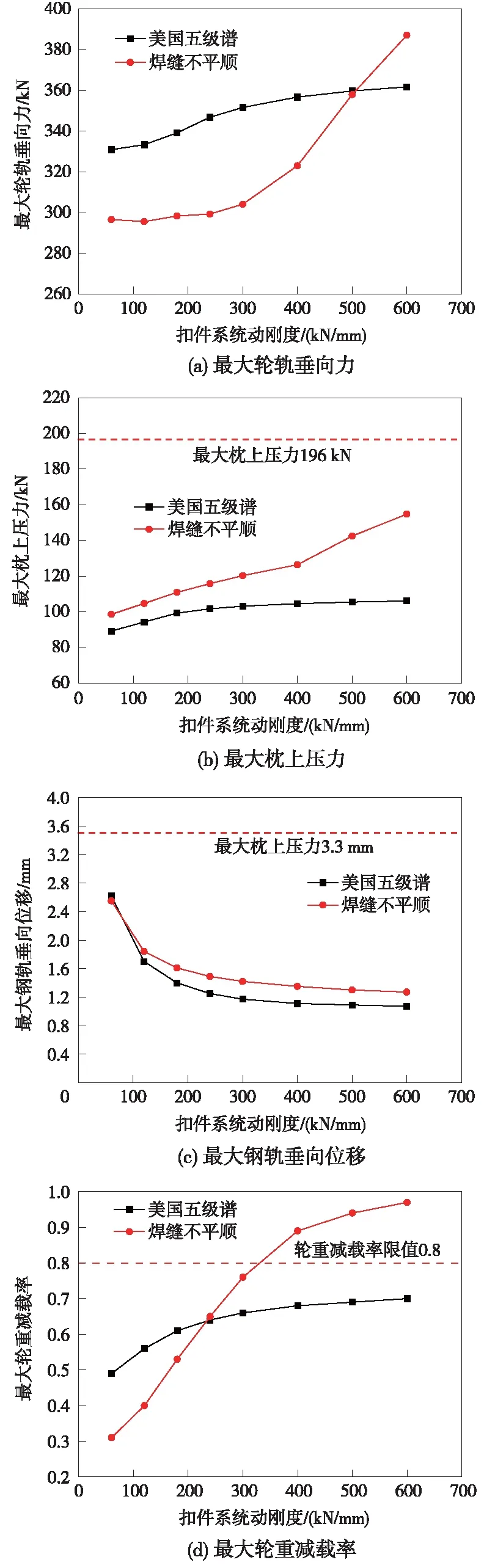
圖6 兩種工況最大動力響應匯總

由圖6統(tǒng)計出各動力響應變化率如表2～表4所示。

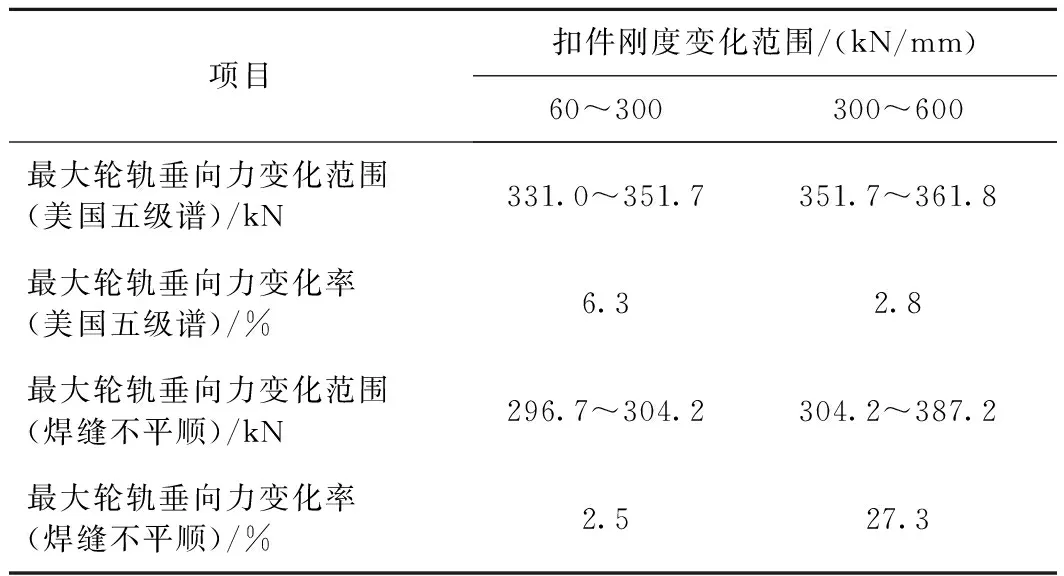
表2 最大輪軌垂向力變化率

由圖6(a)可知，在鋼軌焊縫不平順激勵下，最大輪軌垂向力先隨扣件系統(tǒng)動剛度緩慢增加，而當剛度達到300 kN/mm后陡然上升。由表2可知，當扣件剛度由60 kN/mm增至300 kN/mm、由300 kN/mm增至600 kN/mm時，最大輪軌垂向力增長率分別為2.5%、27.3%。且從圖6(d)看出，在鋼軌焊縫不平順激勵下，最大輪重減載率在扣件剛度300 kN/mm時達到了0.76，逼近輪重減載率限值0.8。鑒于輪軌垂向力是引起車軌耦合系統(tǒng)隨機振動、沖擊、疲勞破壞的直接根源，直接影響到列車運行平穩(wěn)性和安全性[22]，出于以上兩方面考慮，建議扣件系統(tǒng)動剛度不超過300 kN/mm。最大枕上壓力變化率見表3。

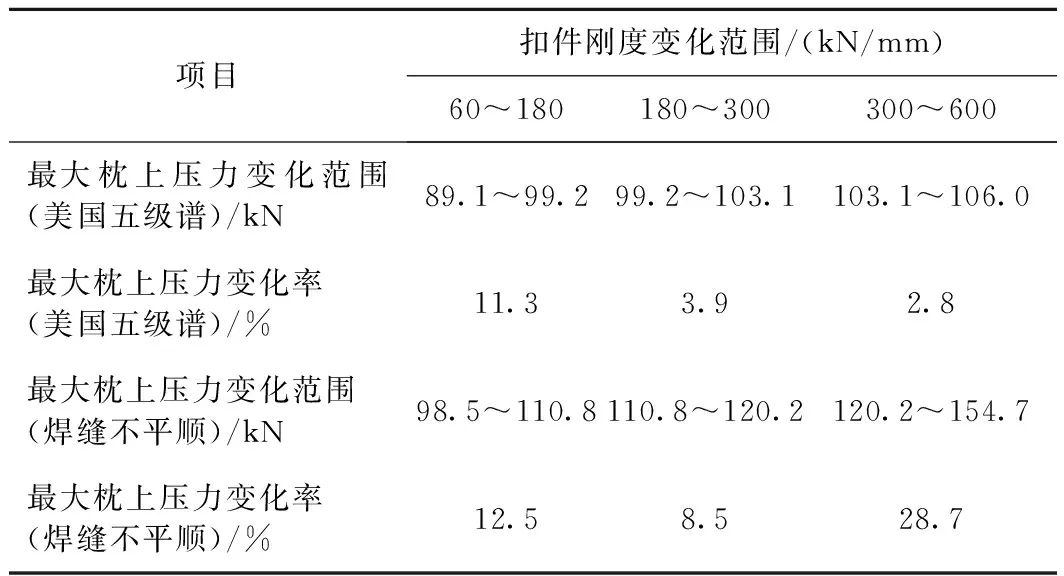
表3 最大枕上壓力變化率

由表3可知，在美國五級譜激勵下，當扣件系統(tǒng)動剛度由60 kN/mm增至180 kN/mm時，最大枕上壓力由89.1 kN增至99.2 kN，增長率為11.3%；當剛度從180 kN/mm增至300 kN/mm及300 kN/mm增至600 kN/mm時，其增長率分別為3.9%及2.8%。而在鋼軌焊縫不平順激勵下，最大枕上壓力增長率依次為12.5%、8.5%及28.7%。綜合兩種工況，為避免枕上壓力過大影響軌下部件的使用壽命，且使其處于一個較為穩(wěn)定的狀態(tài)，建議扣件系統(tǒng)動剛度范圍為180～300 kN/mm。最大鋼軌垂向位移變化率見表4。

由表4可知，當扣件剛度由60 kN/mm增至240 kN/mm時，美國五級譜激勵下最大鋼軌垂向位移減少率為52.3%，鋼軌焊縫不平順激勵下減少率為41.6%。而當剛度從240 kN/mm增至600 kN/mm時，美國五級譜激勵下最大鋼軌垂向位移從1.25 mm降低至1.07 mm，減少率為14.4%；鋼軌焊縫不平順激勵下最大鋼軌垂向位移從1.49 mm降低至1.27 mm，減少率為14.8%。為使鋼軌位移處于一個較小的水平且受剛度波動影響較小，扣件系統(tǒng)動剛度應不小于240 kN/mm。

表4 最大鋼軌垂向位移變化率

綜上，建議45 t軸重重載鐵路有砟軌道扣件系統(tǒng)動剛度范圍為240～300 kN/mm。

3 結論

通過鋼軌容許應力法及軌道容許變形法，分析45 t軸重重載鐵路有砟軌道扣件系統(tǒng)靜剛度合理取值范圍，建立45 t軸重重載貨車-有砟軌道空間耦合動力學模型，分析在不同輪軌系統(tǒng)激擾、不同扣件剛度下該耦合系統(tǒng)動力響應變化，提出了扣件系統(tǒng)動剛度合理取值范圍。主要結論如下。

(1)為使不同道床剛度范圍內的鋼軌下沉位移均能滿足2.5～3.3 mm要求，扣件系統(tǒng)靜剛度范圍應為200～240 kN/mm。

(2)在美國五級譜激勵下，除鋼軌垂向位移隨扣件系統(tǒng)動剛度增大而減小外，其他3個指標均隨剛度增大而增大，且扣件系統(tǒng)動剛度對輪軌垂向力、枕上壓力影響較小，而對鋼軌垂向位移、輪重減載率影響較大。

(3)通過綜合比較最大輪軌垂向力、最大枕上壓力、最大鋼軌垂向位移及最大輪重減載率4個指標在美國五級譜及鋼軌焊縫不平順激勵下，不同扣件系統(tǒng)動剛度的變化范圍，建議扣件系統(tǒng)動剛度范圍為240～300 kN/mm。