一道美國數學競賽題的推廣
2022-10-10 08:26:18廣東省深圳市深圳中學518001邱際春
中學數學研究(江西) 2022年10期
關鍵詞:比賽
廣東省深圳市深圳中學 (518001) 邱際春
2016年AMC12B中第20題是如下組合計數問題:
原題呈現A set of teams held a round-robin tournament in which every team played every other team exactly once. Every team won 10 games and lost 10 games; there were no ties. How many sets of three teams {A,B,C} were there in which A beat B, B beat C, and C beat A?
(A)385 (B)665 (C)945
(D)1140 (E)1330
原題譯文若干支球隊進行循環賽,即每組球隊與其他球隊各進行一場比賽.已知每組球隊贏了10場比賽且輸了10場比賽,每場比賽中不出現平局.在三支球隊組成的集合{A,B,C}中,A贏了B,B贏了C,C贏了A,請問有多少個這樣的集合?
(A)385 (B)665 (C)945
(D)1140 (E)1330

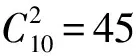
顯然,這種情況是可能的:將各球隊圍成一個圓圈,并且按順時針的順序使得每支球隊均打敗接下來的10支球隊.
評注:此題有一定難度,關鍵是對題目的理解的把握,如果能從題干中獲知循環賽的球隊數,那么根據循環賽的規則就不難得到本題答案為A.
若考慮將每組球隊輸或贏的比賽場數推廣至n場,則原題可作如下初步推廣:
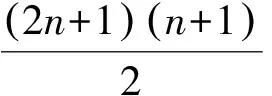
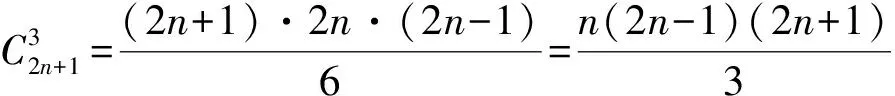
若將原題中滿足給定條件的三支球隊組成的集合{A,B,C}推廣至k支球隊組成的集合{a1,a2,…,ak},則可進一步得到下面的推廣2:

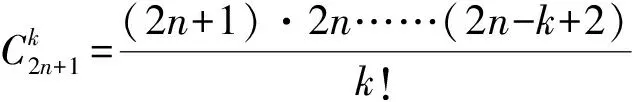
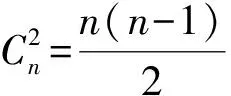

猜你喜歡
小獼猴智力畫刊(2022年4期)2022-05-23 13:48:12
環球時報(2022-03-21)2022-03-21 19:19:19
數學小靈通(1-2年級)(2021年12期)2021-12-30 06:28:04
數學小靈通(1-2年級)(2021年5期)2021-07-21 03:08:14
幽默大師(2020年10期)2020-11-10 09:07:10
小學生(看圖說畫)(2019年12期)2019-12-21 01:55:56
大灰狼(2019年4期)2019-05-14 16:38:38
作文成功之路·小學版(2019年11期)2019-01-14 01:57:15
小天使·一年級語數英綜合(2017年10期)2017-10-31 22:30:38
小雪花·小學生快樂作文(2016年11期)2017-01-09 22:11:33

