基于改進混合長度尺度的機翼延遲分離渦模擬

丘德新，王良軍，張 武, 3*

(1. 上海大學 力學與工程科學學院，上海 200072； 2. 上海大學 信息化工作辦公室，上海 200444；3. 上海大學 上海市應用數學和力學研究所，上海 200072)

0 引 言

飛機在大迎角飛行時，往往伴隨復雜的分離流問題，機翼表面會出現明顯的渦破裂現象。飛機前飛過程中，機翼翼尖會產生持續且較強的渦，在機翼后緣遠場處能觀察到較為明顯的翼尖渦旋。近些年，關于翼尖渦的風洞實驗研究相對較多，Dghim等采用實驗的方法研究了NACA0012機翼的翼尖渦與遠場格柵生成湍流的相互作用。García-Ortiz等在固定迎角= 9°的條件下，研究了展向連續射流對NACA0012機翼尾渦的影響。Lee等研究了近地面處機翼翼尖渦的流動特性。Qiu等采用PIV技術，研究了NACA0015矩形機翼在尾跡六倍弦長范圍內所產生翼尖渦的演化。除了實驗方法，計算流體力學(Computational Fluid Dynamics，CFD)方法也是重要的研究手段之一，其不僅可以降低經濟成本，還可以縮短研究周期。Lombard等介紹了基于大渦模擬方法的翼尖渦形成和演化的數值研究。Pereira等分別采用雷諾平均Navier-Stokes(Reynolds Averaged Navier-Stoke，RANS)方程和尺度解析模擬(Scale-Resolving Simulation，SRS)模型對翼尖渦流動進行了數值模擬。

目前工程上主要的研究方法是通過求解RANS方程進行數值模擬，但RANS只能對湍流的平均矢量場和標量場進行預測，而且RANS計算的渦粘性較大，不能預測湍流的脈動場，對研究細小渦結構和大迎角分離流等問題仍具有局限性。直接數值模擬(Direct Numerical Simulation，DNS)能獲得幾乎所有尺度的流動信息，但其要求極高的網格分辨率，計算量巨大。而大渦模擬(Large Eddy Simulation，LES)方法與RANS和DNS不同，該方法可以將流動分為大尺度流動和小尺度脈動。大尺度區流動受外部因素的影響較為強烈，需進行直接求解，而對小尺度區的湍流脈動進行模化。LES采用的是空間濾波技術，過濾掉小于截止尺度的渦，能夠有效地處理圓柱繞流、 大迎角分離流等復雜湍流問題。然而，在邊界層內層渦尺度較小，難以模化，其大部分湍流能量主要集中在小尺度渦中，因此，計算量仍然十分巨大。考慮到計算資源限制及節省計算成本，同時為了精確地模擬復雜流動問題，采用RANS-LES混合方法是一種較好的選擇。該方法結合了RANS在邊界層內層計算效率較高以及LES在大分離區精度較高的優點，是目前計算大迎角分離流、 自由射流等問題應用較為廣泛的方法。

分離渦模擬(Detached Eddy Simulation，DES)類方法是RANS-LES混合方法中比較有代表性的一種方法。1997年，Spalart等首次提出基于Spalart-Allmaras(S-A)湍流模型的DES方法。但DES存在一定的缺陷，若網格加密不當，在極端情況下會出現網格誘導分離(Grid Induced Separation，GIS)等現象。隨著研究的不斷深入，當分離區較窄或邊界層較厚時，由于LES對邊界層的入侵，可能會引發模化應力衰減(Modeled-Stress Depletion，MSD)等現象。為了消除此類現象，Spalart等對原來的DES進行了改進，提出延遲分離渦模擬(Delayed Detached Eddy Simulation，DDES)的方法，在一定程度上防止了LES入侵到邊界層。

大量的研究表明，DES在復雜分離流等問題中的應用較為成功，相比于LES，其計算成本較小。雖然原始DDES在一定程度上改善了“灰區”問題，在計算中小迎角分離流、 強剪切流等問題時，壁面邊界層以及鄰近區域的網格通常為各項異性網格，其表現為法向網格尺寸遠小于流向和展向的網格尺寸。由于DDES的網格尺度采用的是網格邊長的最大值，有可能造成剪切層區域模化的渦粘性過大，進而導致RANS到LES轉換的顯著延遲。因此，為了改善DDES從RANS過渡到LES的特性，本文基于開源平臺OpenFOAM，對DDES的混合長度尺度進行改進，研究NACA0012半展長矩形機翼在產生分離流時的湍流渦結構以及翼尖渦的生成發展。

1 數值方法

1.1 DDES方法

基于S-A湍流模型的DES方法是在S-A湍流模型的基礎上，對破壞項進行了修改，將壁面距離替換為廣義長度尺度：

=min(,),=max(Δ, Δ, Δ)

(1)

修改后的長度尺度使得S-A湍流模型只在壁面附近起作用，而在其他區域轉變為與網格尺度相關的類Smagorinsky亞格子應力模型。

基于S-A湍流模型的DES方程為

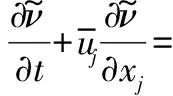
(2)

為了防止LES提前進入邊界層，Spalart等在原DES長度尺度中引入邊界層識別函數，得到混合長度尺度：

=-max(0,-)

(3)

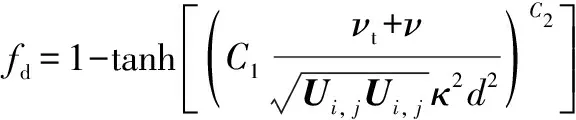
(4)

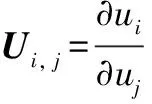
在計算分離流問題時，RANS到LES的轉換需要一定的時間和空間的發展，尤其在分離初期，由于二維剪切層區域模化的渦粘性較大，非定常的特性較弱，延遲了RANS到LES的轉換。為了改善分離初期RANS到LES的轉換特性，降低特定區域的渦粘性，Shur等對RANS-LES混合方法中的LES長度尺度進行改進，首先對網格尺度進行修正，得到新的網格尺度：

(5)

式中：=/||×，為渦量。

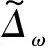
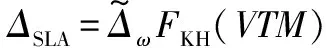
(6)

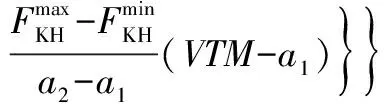
(7)

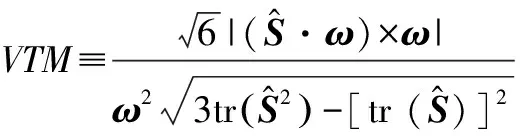
(8)

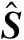
1.2 RANS-LES混合長度尺度修正

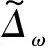
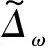
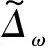
(1) 對于邊界層附近的“扁平”網格，采用上述網格尺度：

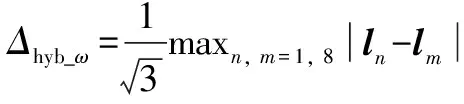
(9)

(2) 對于四面體、 金字塔形、 三棱柱、 正六面體等各項同性網格，則將網格尺度定義為網格單元體積的立方根, 即

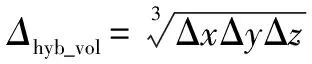
(10)

圖1為網格尺度類型判定流程圖。計算網格為任意網格類型的非結構化網格，為了識別出邊界層附近的各向異性網格，首先對每個控制體單元的面數進行判定。若控制體單元面數為6，則根據網格長寬比判定是否為各向異性網格。網格長寬比大于閾值，則采用網格尺度，否則均采用網格尺度。

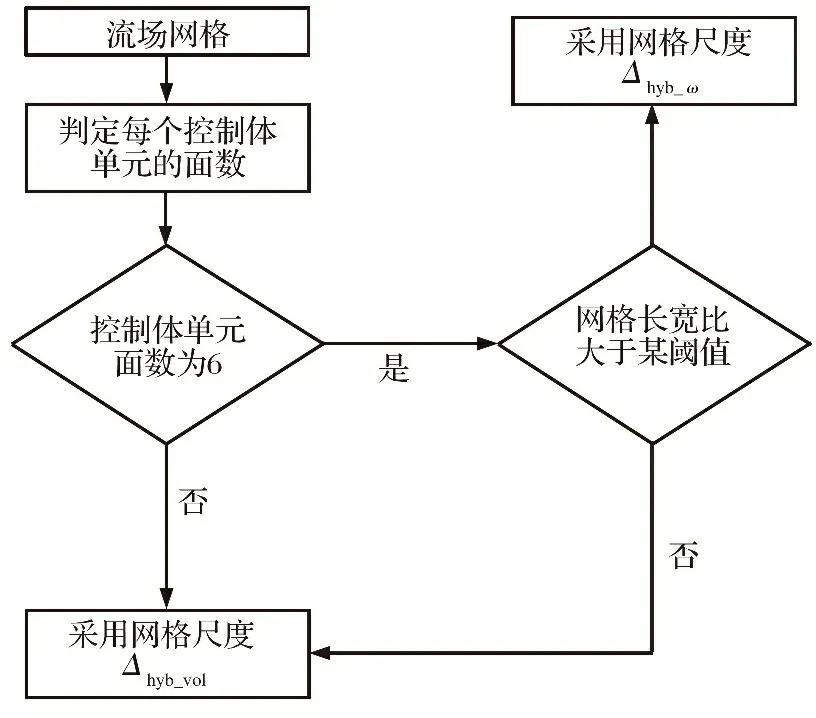
圖1 網格判斷及混合網格尺度流程圖

1.2.2 渦探測函數修正

為了避免()在遠場無粘區及湍流邊緣區開啟，Shur等對進行了修正：

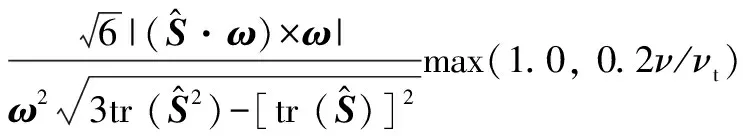
(11)

考慮到邊界層附著流的數值安全性，避免()在邊界層區域中開啟，引入式(4)延遲函數中的，對式(11)進行修正：

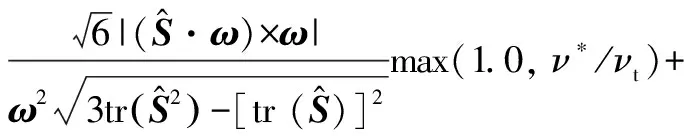
tanh[()]

(12)

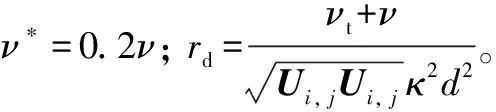
本文對OpenFOAM中現有的S-A DDES湍流模型進行修改，植入了和能夠分辨二維剪切層的函數()，并實現了混合網格尺度方法。

2 數值實驗與分析

在128核的高性能計算服務器下進行計算，總物理內存為256 GB，處理器型號為AMD EPYC 7702。

2.1 NACA0012翼型驗證

為驗證改進混合長度尺度的有效性，采用基于修正長度尺度的S-A DDES方法對NACA0012翼型進行計算。數值實驗馬赫數為0.15，來流迎角為18°，弦長及展長均為1 m。基于弦長的雷諾數為6×10，計算網格如圖2所示，采用非結構混合網格，并在NACA0012局部區域進行網格加密，以更好地捕捉流動細節，網格單元總數約為200萬。

圖2 NACA0012翼型網格

圖3給出了18°迎角的NACA0012翼型在某時刻和()的分布情況。根據分布云圖可知，在背風區，對準二維剪切層的判斷起到了作用，且有效避免了()在邊界層區域開啟，保證了邊界層附著流的數值安全性。由于需要避免()在遠場無粘區及湍流邊緣開啟，在這些區域引入的判斷函數max(1.0,)值較大，因此，值也較大，在湍流邊緣可以發現明顯的邊界。根據()分布云圖可知，在流動分離初期，剪切層區域的值趨于閾值=0.1，在流動分離的下游大部分渦破碎區域及遠場區域的值趨于閾值=1。

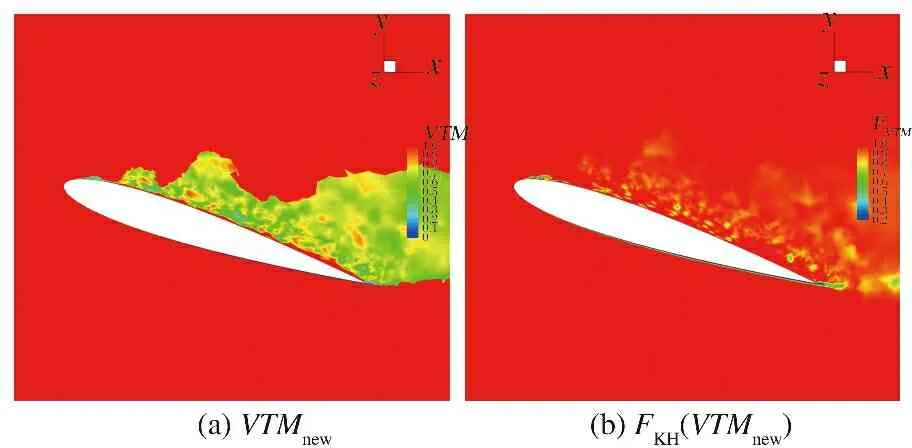
圖3 VTMnew和FKH(VTMnew)分布云圖

NACA0012翼型在18°迎角時已經為失速狀態，表1給出了RANS以及基于的DDES方法與實驗結果的升力系數對比，DDES方法所得的為計算穩定后的平均值，實驗結果來自McCroskey所提供的數據。根據對比結果可知，由于流場具有明顯的非定常特性，RANS對的預測有一定的延遲，而基于的DDES計算結果雖然略小于實驗值，但誤差相對較小。

表1 升力系數CL對比

圖4為同一時刻不同位置的渦量(-vorticity)等值面，根據圖4可以發現翼型背風面為大分離區。由于翼型表面附近具有更密集的網格，可以解析出更精細的渦結構。背風區的渦旋運動較為復雜且具有隨機性。在背風區下游可以清晰觀察到大渦結構以及正、 負渦量交替脫落現象。

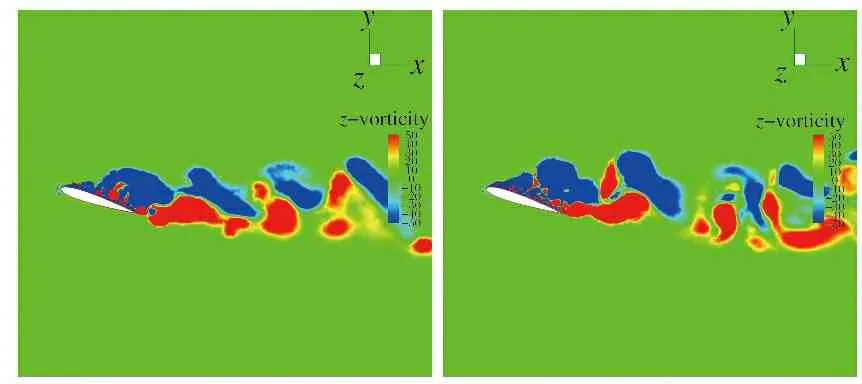
圖4 瞬時渦量云圖

2.2 半矩形翼計算

為研究小迎角分離以及翼尖渦的形成與演化過程，計算模型基于JAXA的NACA0012矩形機翼風洞實驗模型，機翼弦長為0.4 m，半翼展長為1 m，其中翼尖為不帶翼梢小翼的鈍體翼尖，雷諾數為1.8×10，馬赫數為0.175。根據實驗研究表明，機翼迎角為12°時，在機翼尾緣附近能夠觀察到流動分離，因此，計算也采用12°迎角。

為了驗證NACA0012矩形機翼的網格無關性，計算了三套不同疏密程度的非結構化網格，如表2所示，細網格的網格量約為粗網格的4.5倍。

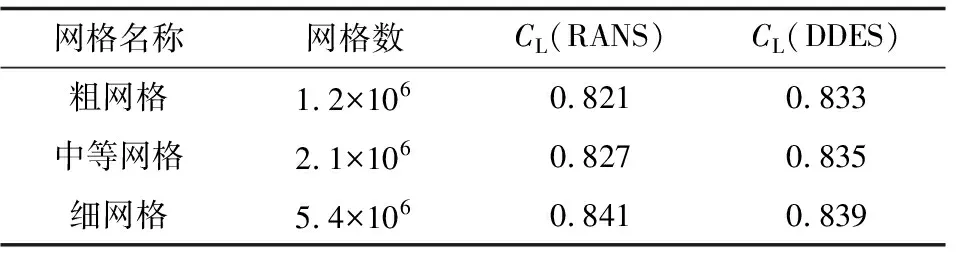
表2 NACA0012機翼網格無關性驗證

由表2可知，RANS方法計算的最大相對誤差約為2.44%，基于的DDES方法計算的最大相對誤差約為0.72%。對于細網格，兩種方法計算的相對誤差約為0.24%。可以認為計算結果達到了網格收斂，在之后的計算中主要采用中等網格和細網格。

為了提高網格類型復雜度，計算采用混合網格，在機翼表面附近采用六面體以及三棱柱網格，其他區域采用四面體以及金字塔形網格。圖5(a)為對稱面和機翼表面網格，圖5(b)為機翼翼端處表面網格。為了更好地捕捉在機翼翼尖和后緣附近渦結構，對機翼所在區域尤其在機翼翼尖周圍進行局部加密，網格數大約為210萬，即中等密度網格。為了保證在機翼表面湍流附面層計算的準確性，第一層網格點與機翼表面之間的距離滿足+小于1。

首先，采用RANS對NACA0012機翼進行計算，以獲得機翼穩態流動特性。采用S-A湍流方程模型； 對流項采用高斯迎風格式； 擴散項采用高斯線性格式； 矩陣求解器采用預條件共軛和穩定化預條件雙共軛求解器； 速度-壓力耦合采用SIMPLE算法。

圖5 NACA0012機翼網格

為減小計算時間和保證計算精度，將RANS的穩態結果作為DDES的初始條件，分別采用原S-A DDES方法和改進RANS-LES混合長度后的S-A DDES方法進行模擬。對流項采用混合格式，在渦主導的流動分離區域采用低耗散線性格式，而在遠場無粘無旋區采用迎風格式，保持足夠耗散以提高計算穩定性。擴散項采用高斯線性格式； 時間項采用Crank-Nicolson方法進行離散； 速度-壓力耦合采用PIMPLE算法。為確保計算的穩定性，采用自動調整時間步方法并保證最大庫朗數小于1。

圖6為12°迎角下RANS、 原S-A DDES、 基于的DDES方法機翼表面及翼尖處的渦量等值面云圖(=30 000 s)，采用流向的速度分量進行著色。其中，圖6(a)RANS方法是在計算達到收斂時候的結果，而原DDES和基于的DDES方法的渦量等值面是在計算初期相同時刻的結果。比較圖6(b)和圖6(c)可以發現，分離初期由于原DDES方法在剪切層區域模化的渦粘性較強，抑制了RANS到LES的轉換，以至于在機翼表面的渦結構與RANS方法計算的渦結構類似，僅在機翼尾緣處有少量細小渦結構。而基于的DDES方法實現了RANS到LES的快速轉換，在機翼背風區可以清楚地觀察到剪切層的快速失穩，旋渦已不再是一個整體而是分散的細小渦結構。對比圖6在翼尖處的渦量等值面發現，三種方法的計算結果相似，都清晰地顯示了渦在翼尖處卷曲并旋轉拖出較長的尾渦。由于在翼尖區域的網格較為粗糙，基于的DDES方法的計算結果并未展現出更多的細節。

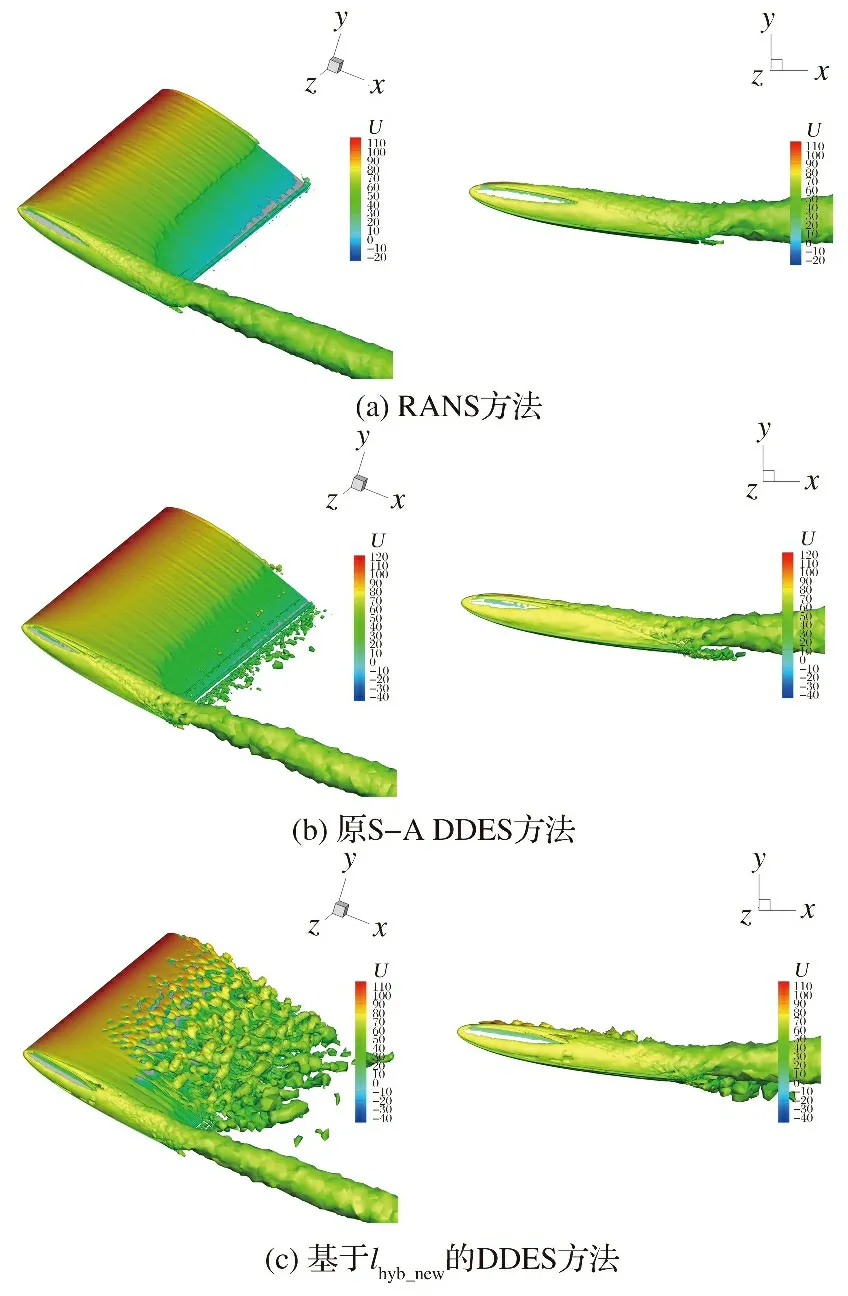
圖6 12°迎角機翼表面Q渦量等值面

因此，為了進一步驗證改進混合長度尺度的有效性，對計算網格進行加密，尤其在機翼背風區及翼尖處，減小了網格尺寸并擴大了加密區域。加密后的網格數大約為540萬。圖7為網格加密后的機翼翼根處截面壓力系數計算結果對比。結果表明，基于的DDES方法和RANS方法的計算結果與實驗結果較為吻合。圖8(a)為基于的DDES方法計算得到的在翼尖周圍的流線圖。其中，紅線表示主渦再附著線，藍線表示次渦分離線。與圖8(b)實驗油流圖對比可以看出，計算結果與實驗結果較為吻合。

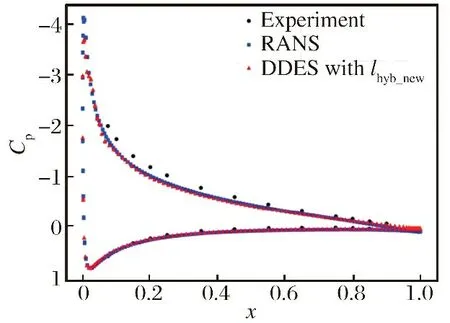
圖7 翼根處機翼表面壓力系數

圖8 翼尖周圍流線圖對比

圖9給出了細網格基于的DDES方法的機翼表面及翼尖處的渦量等值面云圖(=30 000 s)。從圖中可以看出，在翼尖處進行網格加密后得到的渦結構展現出更多的細節。根據已有研究可知，翼尖周圍的流場與雙渦結構有關。機翼上表面的渦稱為主渦旋，翼尖和下表面的渦稱為次級渦以及次級尾跡渦。機翼前緣翼尖下表面處的渦管比上表面的渦管強，下表面渦管逐漸在尾緣處分成數根渦管并逐漸上翻演變，在尾緣處與上表面渦管“擰”成螺旋狀并在后方形成一條大渦管。翼尖渦結構脫離機翼表面并向下游遠場處傳播，在尾跡區某一位置形成閉環結構。

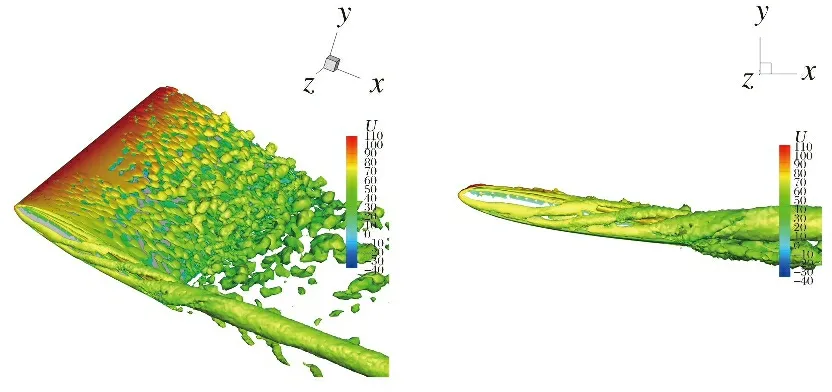
圖9 基于lhyb_new的DDES方法的Q渦量等值面

圖10給出了翼尖處不同截面流向渦量。從圖中能夠更清楚地觀察到翼尖渦的形成細節，在機翼前緣翼端表面有正渦量產生，但從機翼下表面卷起的負渦量更為明顯。機翼上表面的正渦量直徑沿流向有一定的增大，而下表面負渦量反向旋轉至上表面并且增長更為迅速。結合圖9中的渦量等值面，下表面的渦管在機翼尾緣上翻形成螺旋狀的不穩定現象，此時與周圍的流體產生充分的能量交換。

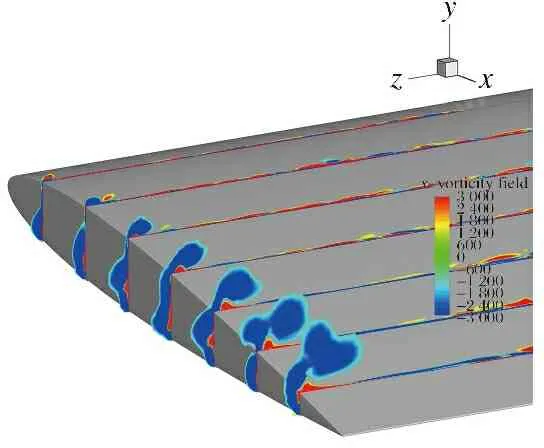
圖10 機翼翼端不同截面流向渦

由于翼尖處上下表面渦旋的相互作用，在機翼尾緣處形成了較為明顯的尾跡渦，如圖11所示。在脫離翼端尾緣后尾跡渦繼續向上翻卷，渦核不斷增大，在距離尾緣大約兩倍弦長的位置，尾跡渦與渦量層發生分離，并在遠場處逐漸耗散。圖12顯示了尾跡流向渦隨不同截面的演化過程，在尾緣處能清楚地觀察到渦量層正負渦量的交替過程。在機翼下游，渦量層不斷向尾跡渦進行供給并沿軸負方向移動。

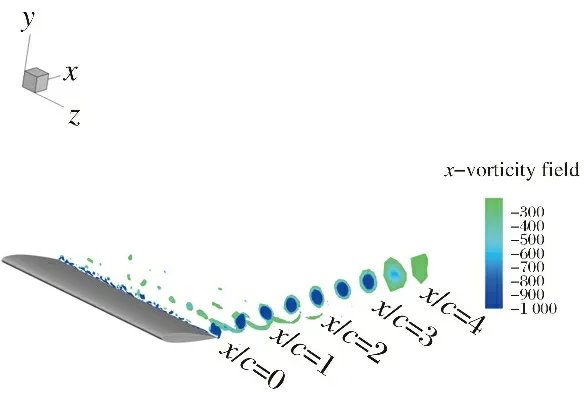
圖11 近翼流場尾跡流向渦

為了驗證本文方法在計算半展長矩形機翼大迎角分離流問題時的有效適應性，對18°迎角的NACA0012矩形機翼進行數值模擬。圖13為RANS方法及基于的DDES方法計算得到的渦量等值面云圖。根據計算結果可知，機翼在18°迎角時具有更明顯的非定常特性，且比12°迎角的機翼具有更明顯的渦結構。對比RANS方法的渦量等值面云圖可以發現，改進后的DDES方法在機翼背風區能夠捕捉更精細的渦系結構，且在翼尖處能夠清晰地看到渦破裂現象，也進一步證實了該方法的有效性。

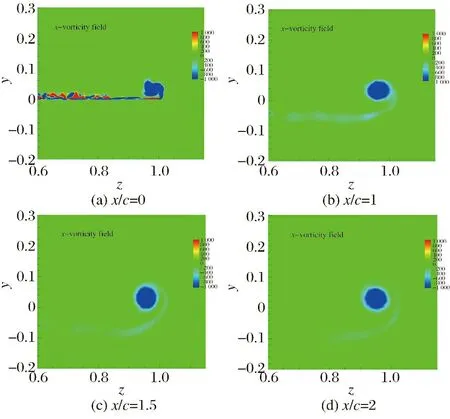
圖12 機翼尾跡不同截面流向渦

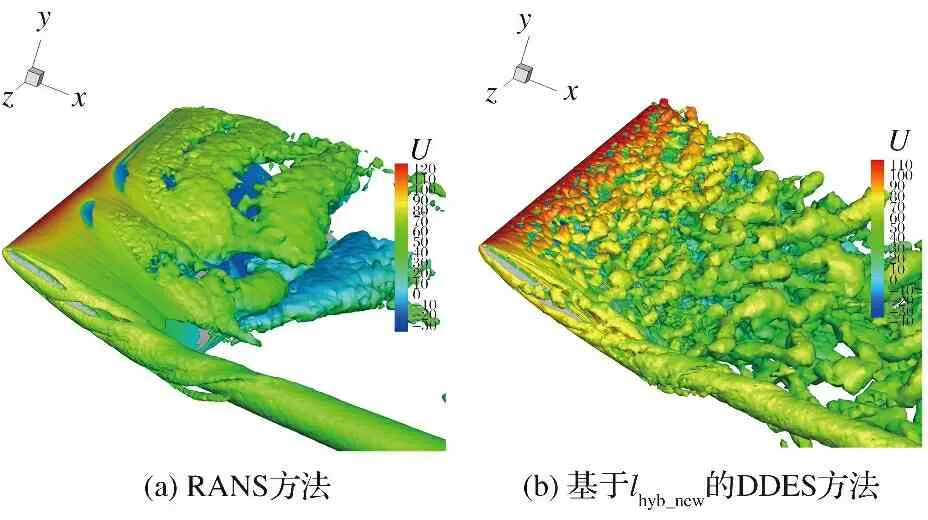
圖13 18°迎角機翼表面Q渦量等值面

3 結 論

本文基于開源CFD平臺OpenFOAM的不可壓縮求解器pimpleFoam對中小迎角分離流問題進行了數值模擬。研究了S-A DDES方法中采用混合網格尺度和修正渦探測函數對加速RANS到LES的轉換效果。通過對比研究得出以下結論：

(1) 通過對18°迎角NACA0012翼型的數值實驗，分析和驗證了基于修正后的渦探測函數和能夠分辨二維剪切層的函數()在S-A DDES模型中的有效性。

(2) 對12°迎角NACA0012機翼繞流進行了數值計算，對比了S-A、 原S-A DDES和改進RANS-LES混合長度后的S-A DDES三種湍流模型的渦量等值面，驗證了修正后的混合長度尺度對DDES方法加速RANS到LES轉換的有效性。

(3) 采用改進后的方法對細網格進一步計算，更精細地模擬了在機翼背風區與翼尖處的流場。對比分析了機翼翼根截面處的壓力系數，與實驗結果較為吻合，并分析了翼尖渦在生長階段的演化過程。