基于大樣本的電動汽車行駛工況構建方法研究

陳 寶，黃 春，謝光毅，付江華，黃澤好

(重慶理工大學 車輛工程學院，重慶 400054)

0 引言

國外行駛工況較成熟，美國、歐洲、日本分別使用FTP75、NEDC、JAPAN10-15作為本國標準行駛工況[3-4]。2019年10月，中國國家市場監督管理總局,針對燃油汽車與非插電式混合動力汽車的中國自主汽車行駛工況正式發布，這將為我國車輛能耗、排放測試及產品研發提供重要依據[4-5]。

我國不同地區的交通狀況、駕駛模式不盡相同，使得不同地區的汽車行駛工況存在差異，汽車能耗測試的結果與當地實際行駛工況存在較大偏差[6-7]。因此，這對于不同地區制定符合實際交通狀況的車輛行駛工況十分重要。

當前針對行駛工況的構建，大部分研究學者在車型的選擇上，多采用燃油車、商用車等車輛。由于電動汽車通過電機驅動，其速度、扭矩響應等方面與燃油車存在差異，針對電動車的電池能耗、續航里程等性能評估上，燃油車行駛工況不適用，所以構建電動汽車行駛工況非常重要。

綜上所述，為充分反映電動汽車的實際運行特征。以成都市為例，收集了該市30輛電動汽車3個月的行駛數據，對原始行駛數據進行預處理分析、運動學片段的劃分、特征參數提取，采用主成分分析法以及粒子群算法和K均值聚類算法結合，構建了成都市電動化汽車行駛工況。

1 行駛數據采集與預處理

1.1 行駛數據采集

針對車輛行駛工況構建方法的研究，盡管在試驗規劃、數據采集與處理、工況合成與驗證等方面有所不同，但行駛工況構建的流程基本一致[18]。采用圖1的流程構建成都市電動汽車行駛工況。

圖1 行駛工況構建的流程框圖

為兼顧不同駕駛員的駕駛習慣以及確保所構建的典型工況能真實反映道路特征，采用自主行駛法進行數據采集，即對行駛路線不做具體的規定，駕駛員可根據自身的常行程安排隨機選擇行駛路線[19]。選擇了30輛成都市某型電動汽車，整車主要參數如表1所示。連續采集3個月的行駛數據，采樣頻率為1 Hz，最終獲取了覆蓋442.7 km、3 640 800條有效行駛數據，如圖2。收集的數據主要包括行駛時間、經緯度、車速、加速度、電池SOC、電機轉速、電機轉矩、百公里電耗等參數。由圖3行駛路線經緯度分布可知，行駛路線主要分布在經度為103.9°～104.2°，緯度為30.6°～30.7°附近，試驗車輛主要成都市武侯區、成華區地段活動。

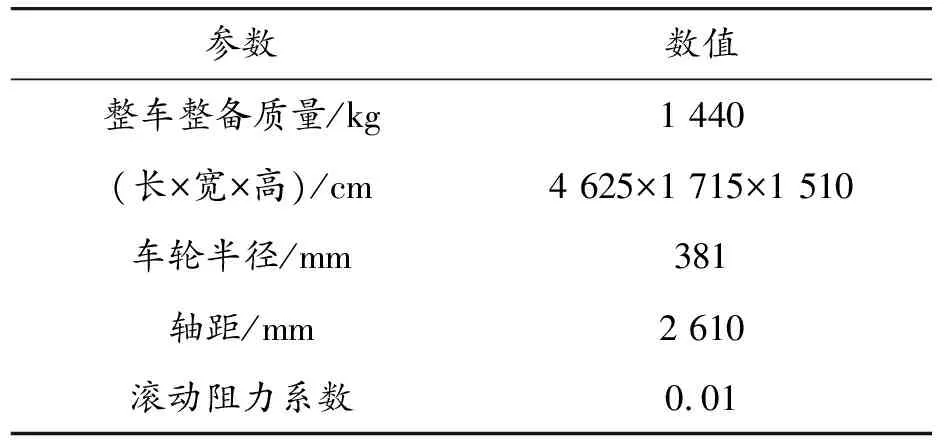
表1 某型電動汽車整車主要參數

圖2 總體樣本車速數據

1.2 行駛數據預處理

在數據采集過程中，采集設備精度、交通環境等因素的影響下，使得數據存在缺失、異常等現象，數據質量有所下降。為保證數據可靠性，需對數據進行預處理分析。

1.2.1GPS信號缺失數據

當車輛經過高層建筑物、隧道等路段時，GPS信號由于受遮擋導致定位不準或者不連續，車速數據有所缺失。采用插值的方法或剔除的方式進行處理后，GPS為0的數據有125個，缺失的數據有1 036個。

1.2.2怠速數據處理

由于長時間堵車或停車，采集的數據并不滿足要求。將汽車斷斷續續行駛，最高車速小于10 km/h，視為怠速；以車速為0且持續時間小于180 s為篩選原則，超過180 s之后的數據直接剔除[20]。經處理，不正常數據達1 777 064個。

1.2.3最高速度、加速度限制

通過圖4可知，汽車主要在城區或郊區行駛，車速限制在120 km/h以內，加速度限制在-6～6 m/s2以內[21]。

1.2.4速度濾波處理

由于外界因素影響下，行駛數據存在異常噪聲干擾現象，使得數據存在誤差。采用滑動平均濾波算法對原始數據進行濾波處理，對原始數據用一個固定長度的滑動窗口，其鄰域內幾個數據的均值來代替相應位置的原始數據，形成一個均值新序列[22]。

(1)

式中：y(t)為平均值，t=1,2,…,n。n為總數據長度，T為時間步長，x(t)為原始速度數據。從圖5中可以看出，在濾波之前，原始速度數據存在尖點峰值，而在濾波之后，速度曲線變得平滑，濾波前后的車速曲線較吻合。

圖4 濾波前后的速度數據

通過上述處理，得到有效數據數據為1 863 736個,原始速度的平均速度為11.87 km/h，平均行駛速度21.94 km/h，處理后的數據的平均速度為16.92 km/h,平均行駛速度23.30 km/h。分析其原因，在數據采集階段，由于測試人員持續對車輛進行汽車NVH、電機等相關測試，收集的數據出現大量的停車段，在怠速數據處理時，進行刪除處理。

1.3 運動學片段劃分及特征參數提取

汽車行駛過程可看作由大量的運動學片段拼接而成，運動學片段是指汽車從怠速開始至下一個怠速開始之間的車速區間，由加速、減速、勻速、怠速工況構成[23]，如圖5。根據國標[5]，由式(2)對原始數據的速度v和加速度a進行運動學片段的劃分：

(2)

圖5 汽車運動學片段示意圖

為準確描述各個運動學片段狀態和特征，選取14個特征參數用于表征汽車行駛工況特征評價體系指標(如表2)；選取3個特征參數用于表征電動汽車的性能特征(如表3)。

表2 行駛工況特征參數

表3 電動汽車性能特征參數

將預處理分析后的1 863 736條行駛數據劃分為8 599條運動學片段，得到特征參數矩陣M8 599×17元素，如表4。

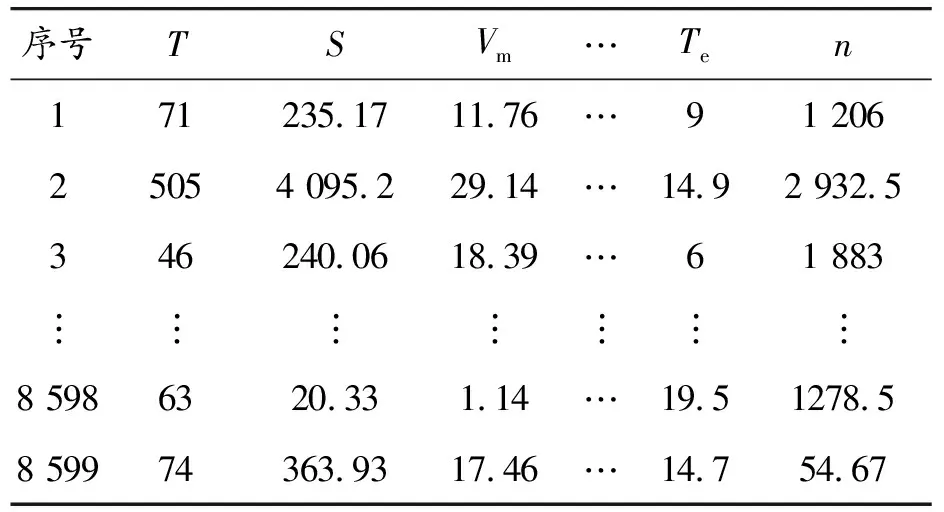
表4 運動學片段特征參數矩陣M8 599×17元素

1.4 主成分分析

在車輛行駛工況的構建過程中，有些特征參數之間并不是相互獨立的，而是存在一定的相關性，應用主成分分析對特征參數進行降維，通過幾個互不相關的主成分去表達原始數據的特征參數所蘊含的信息,可減少在對特征參數矩陣進行聚類分析運算的時間[24]。具體步驟如下:

1) 特征參數標準化處理。為避免特征參數單位不統一而使特征參數取值分散程度較大，影響聚類分析的結果，需對特征參數矩陣M8 599×17標準化處理,如式(3)。

(3)

(4)

2) 計算標準化處理后的矩陣Xij的協方差矩陣C。

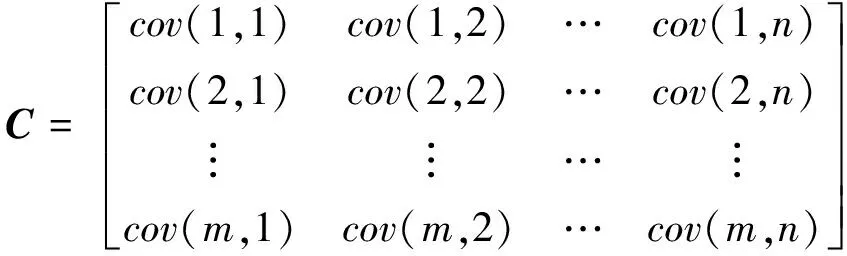
(5)

(6)

式中,cov(x,y)表示為協方差矩陣C的第x行與第y列的協方差。

3) 求解協方差矩陣C的特征值λ和特征向量φ。將特征值λ從大到小排序。計算所有特征值貢獻率ω和累計貢獻率β。貢獻率用來衡量主成分所表達的信息，若貢獻率越大，則主成分所表達的信息越多。

(7)

(8)

式中：ωi為第i個特征值的貢獻率，βk為前k個特征值累計貢獻率，選取累計貢獻率大于80%或特征值大于1的主成分[12]，并確認主成分的個數c。

4) 計算主成分F。

(9)

式中，φi為第i個特征值所對應的特征向量。

綜上，對所提取的運動學片段的特征參數矩陣M8599×17進行主成分分析，得到各個主成分的特征值、貢獻率以及累計貢獻率，如表5所示。

表5 各主成分貢獻率及累計貢獻率

根據主成分個數篩選原則，前5個主成分的累計貢獻率已達到80.68%。各個主成分特征值分布如圖6，當主成分為4時，特征值曲線出現拐點，當主成分個數小于4時，特征值下降的幅度驟減，當主成分個數大于4時，隨著主成分個數的繼續增大而特征值趨于平緩，由于第五主成分的特征值大于1，綜上，選取5個主成分。主成分載荷矩陣元素如表6所示。

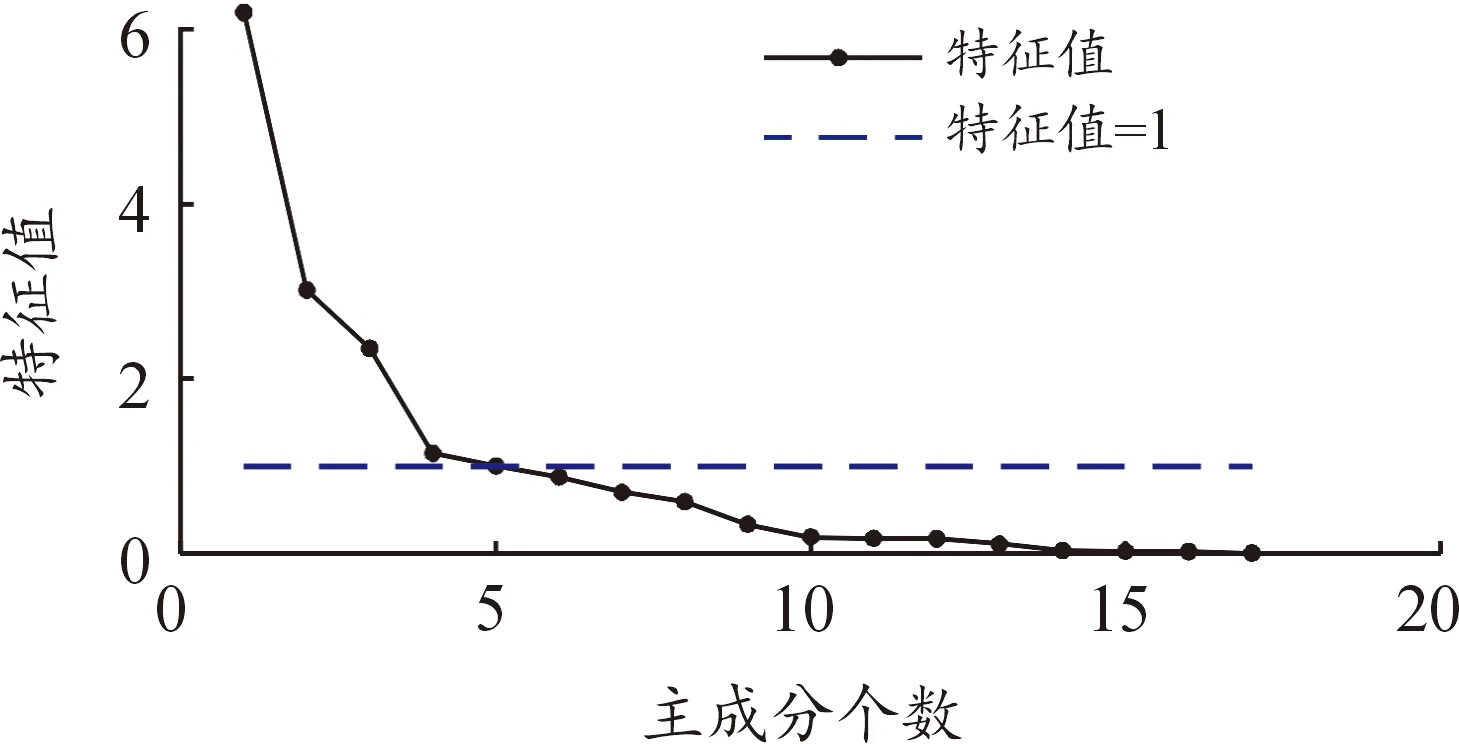
圖6 主成分特征值分布

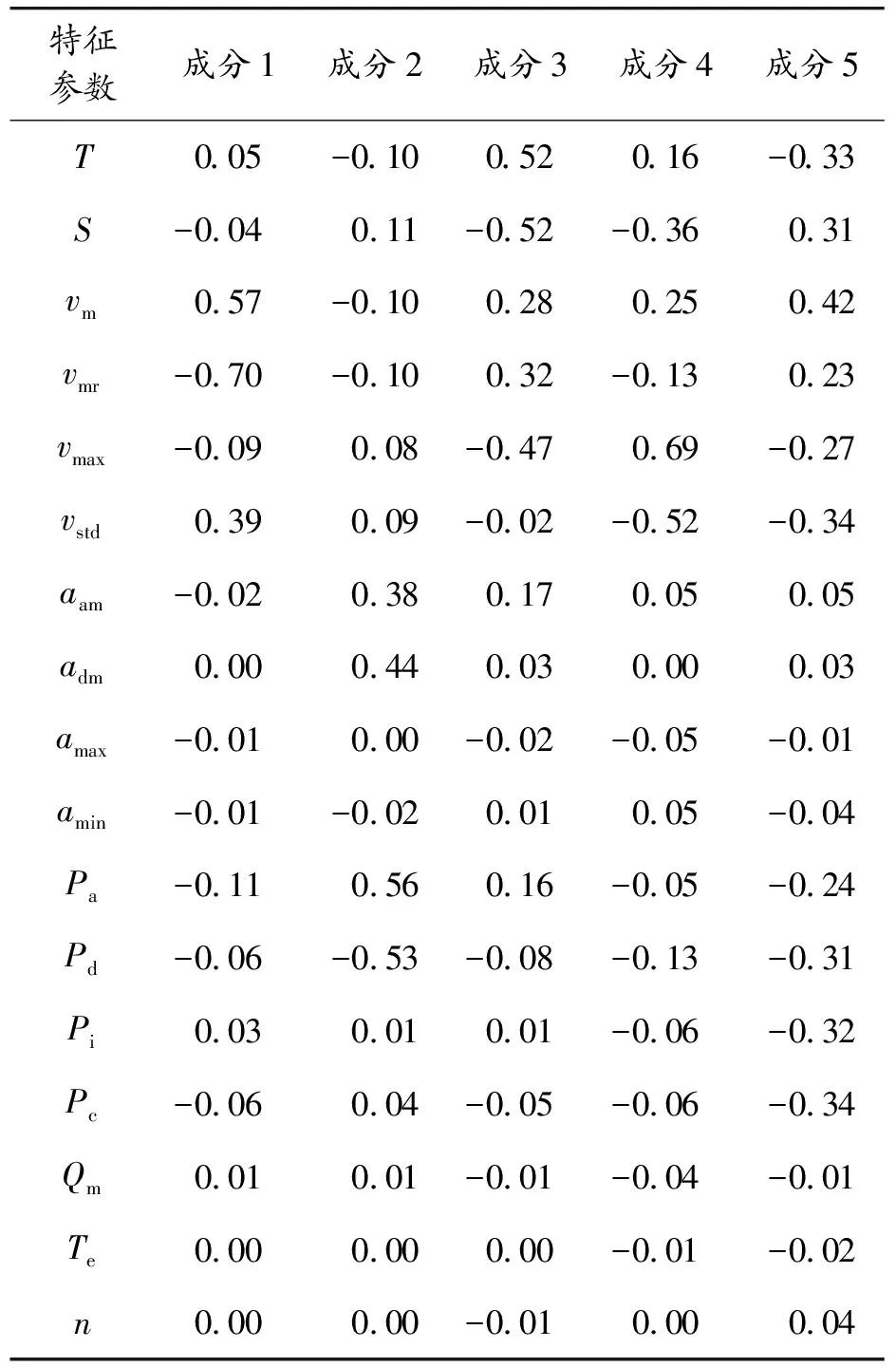
表6 主成分載荷矩陣元素

第一主成分主要反映的是平均速度、速度標準差；第二主成分主要反映的是平均加速度、平均減速度、加速時間比；第三主成分主要反映的是運行時間；第四主成分主要反映的是最大速度，第五主成分主要反映的是運行距離、平均速度、平均行駛速度。基于主成分得分矩陣N8599×5元素，如表7。采用粒子群算法與K均值聚類算法結合的方式，對主成分得分矩陣進行聚類分析。

表7 主成分得分矩陣N8 599×5元素

1.5 改進的K均值聚類分析

K均值聚類(k-means clustering,kmc)通過選定聚類數目k與初始聚類中心，計算各樣本數據與聚類中心之間的最小距離，根據距離遠近,分配樣本數據到最近的聚類中心，不斷迭代選取新的聚類中心并調整各數據類別[13]。

由于K均值聚類算法受初始聚類中心影響，其較弱的全局搜索能力易陷入局部最優，聚類個數憑經驗選取。采用肘部法和Silhouette輪廓系數[12]結合選取聚類數目，結合粒子群算法(particle swarm algorithm,PSO)全局搜索能力，優化初始聚類中心[25]。由于系數和最大速度等參數選取不當，會影響粒子群算法收斂速度和精度。采用調整慣性權重來平衡全局搜索和局部搜索，再使用K均值聚類算法，使初始的聚類中心之間盡可能的遠，進行分類。

基于粒子群K均值聚類算法(PSO_kmc)基本步驟如下:

1.5.1聚類數目的確定

1) Silhouette輪廓系數函數

(10)

式中:α(i)為同一簇中，樣本i與其它樣本的平均距離，即簇內不相似度，b(i)為樣本i的與相鄰最近的一簇內所有點平均距離的最小值，即簇間不相似度。s(i)為輪廓系數，將所有點的輪廓系數求平均，就是該聚類結果總的輪廓系數，s(i)接近1，則說明樣本i聚類合理;當s(i)為0時，則代表兩個簇中的樣本相似度一致，兩個簇為同一個簇;

2) 肘部法(誤差平方和SSE)

隨聚類數k的增大，樣本劃分會更加精細，每個簇的聚合程度會逐漸升高，誤差平方和SSE會逐漸變小。當k小于真實聚類數時，由于k的增大會增加每個簇的聚合程度，故SSE的下降幅度會很大。當k接近真實聚類數時，再增加k,SSE的下降幅度會驟減，隨著k值的繼續增大而趨于平緩。

(11)

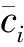
通過處理分析，肘部誤差平方和SSE如圖7，當聚類數目小于3時，誤差平方和急劇下降，聚類數目大于3時，誤差平方和趨向于平和。平均輪廓系數值如圖8，聚類數目為3時，平均輪廓系數最高。輪廓系數曲線如圖9,不同類別下輪廓系數值均有少量負值出現，聚類數目為3時，各類數量分布較為均勻。綜上，選取聚類數目為3。

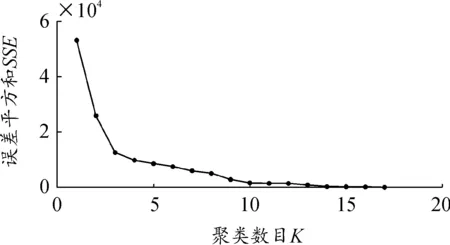
圖7 肘部誤差平方和SSE

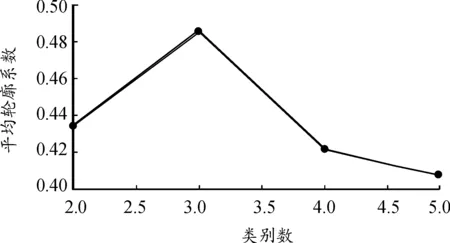
圖8 平均輪廓系數值

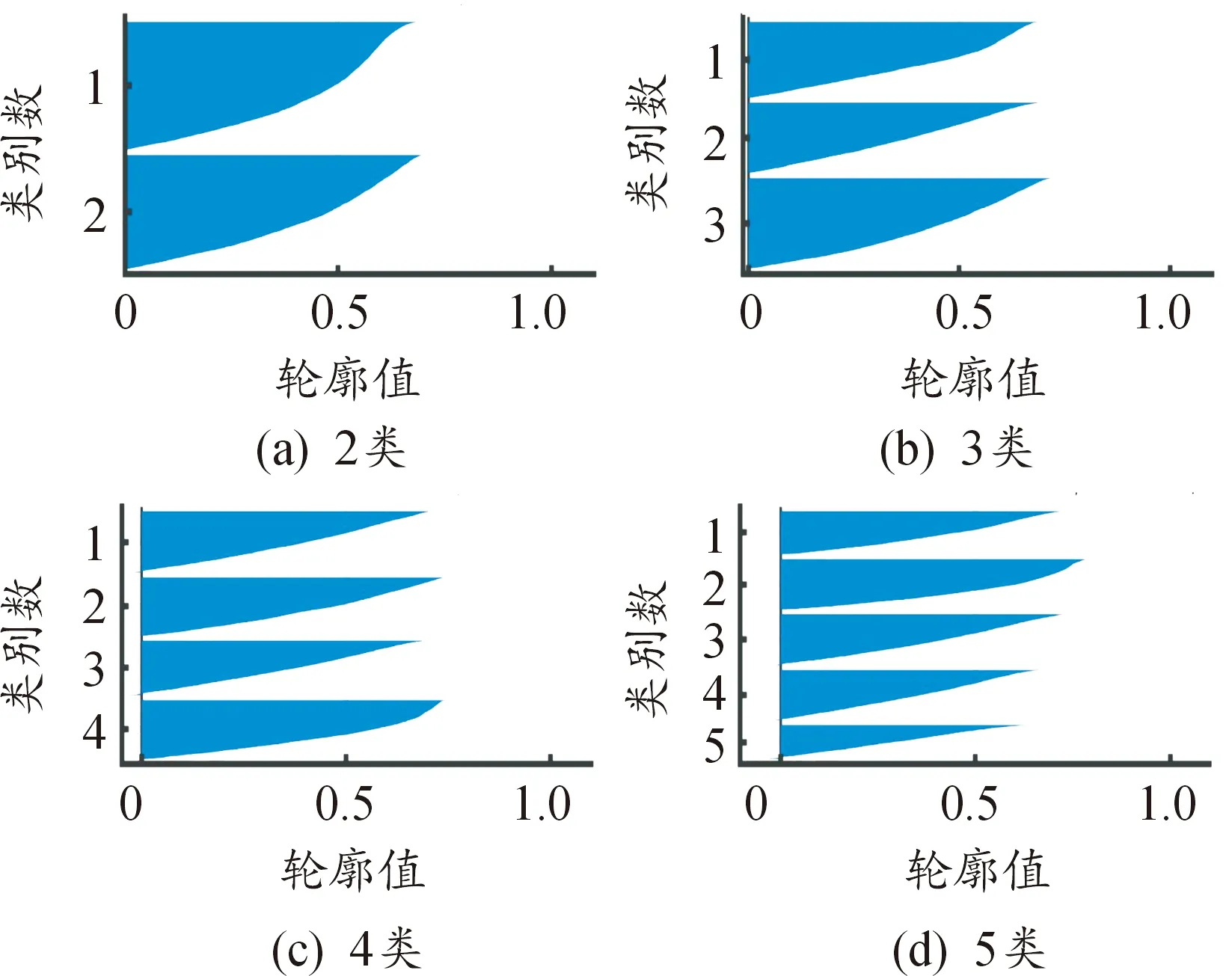
圖9 輪廓系數曲線

1.5.2粒子群算法優化K均值聚類中心

1) 初始化種群。隨機產生粒子初始聚類中心，初始位置xi和速度vi，學習因子bi。

2) 適應度值fi計算。由式(12)計算各類內數據到聚類中心歐式距離fi，作為粒子的個體極值，最小的適應度值作為全局極值。

(12)

式中：i為數據cij所在的類，m為第i個類數據個數，ci為第i類數據聚類中心。

3) 通過式(13)慣性權重實現粒子從粗略的全局搜索到局部的精細搜索，式(14)(15)更新整個粒子群的粒子位置與速度，計算更新后粒子的適應度值。

(13)

(14)

xi(t)=xi(t-1)+vi(t)

(15)

式中：wmax、wmin分別為權重最大和最小值，fbest、fbad分別為粒子最好與最差的適應度值。rand1、rand2為0～1中的隨機數，Pbesti為粒子最佳位置，Gbestd為全局極值。

4) 由式(16)粒子群的適應度方差δ2判斷當前粒子是否達到收斂狀態。fa為粒子群的平均適應度。當δ2小于設定閾值0.1時，則群體趨于收斂。選擇10個最優粒子，進行k均值聚類。

(16)

5) 計算每個樣本與當前聚類中心的歐氏距離,根據距離的大小，進行粒子聚類劃分。在輪盤法基礎上選取下一個聚類中心，更新粒子的適應度值。

6) 判斷適應度值是否最優或達到最大迭代次數，則結束。

由表8，圖10、11、12可得出，第1類中平均行駛距離最短，約77 m，怠速比例最高，速度分布在0～10 km/h，可反映出在城市擁堵路段上運行時的交通特征。第2類中速度分布在10～20 km/h、加速、減速、勻速、怠速時間比較為均和，運行距離適中，可反映出在城市主干道上運行時的交通特征。第3類速度分布在20～40 km/h,運行時間、行駛距離、最高車速、平均行駛車速、最大加速度、最大減速度高于其余兩類，可反映在城市郊區道路上行駛的交通特征。

表8 各類特征值參數

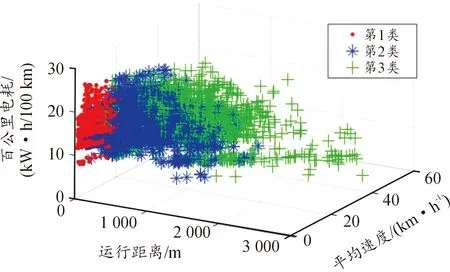
圖10 各類運行距離-平均速度-百公里電耗分布

2 行駛工況構建

根據k均值聚類算法定義，每一類別中的樣本與其聚類中心的距離越小，則表明該樣本越能反映本類別的特點[12]。所構建的成都市城市電動汽車行駛工況時長為1 500 s，根據每類總的行駛時間在總體數據中所占的時間比,可以計算出各類在最終擬合工況中所占的時間，再根據每一類與其聚類中心的聚類從小到大排序，篩選出候選片段[14]。根據聚類結果，第一、二、三類的運動學片段數分別為1 462、4 188、2 949。

(17)

式中：Ti為第i類在最終合成的汽車行駛工況中的時間長度，i=1,2,3,k為類別數，k=3，tij為第i類的第j個片段所持續的時間。

通過計算，第一類、第二類、第三類在最終合成后的行駛工況中的時間長度分別為215、668、619。選取的片段分別為3條低速片段、10條中速片段、7條高速片段。最終構建了持續時間為1 502 s、最高車速為58.4 km/h、總行程為6.723 km的成都市電動汽車行駛工況，如圖13。

圖13 成都市電動汽車行駛工況

3 工況驗證與分析

3.1 運動學片段特征參數誤差分析

通過粒子群算法與K均值聚類結合(pso_kmc)與傳統K均值聚類(kmc)進行工況構建對比，通過式(18)計算了成都市與樣本數據特征參數的相對誤差。

(18)

式中：Ck、Uk分別構建工況和原始樣本數據的第k個特征參數，n為特征參數個數。

由于最高車速、最大加速度、最大減速度偶然性較大，將其進行對比的意義不大。由表9可知，基于粒子群和K均值聚類 (pso_kmc)行駛工況曲線與樣本數據特征參數相對誤差均在5%以下，各特征參數值的平均相對誤差為2.28%。而通過同樣的方式采取傳統的K均值聚類算法(kmc)所構建的工況誤差相對較大，各特征參數值的平均相對誤差為5.82%,由于K均值聚類受初始聚類中心的影響，較弱的全局搜索能力陷入局部最優，致使誤差較大。因此，結合粒子群算法的K聚類提高了工況構建精度。

表9 部分特征參數相對誤差

3.2 速度—加速度聯合分布

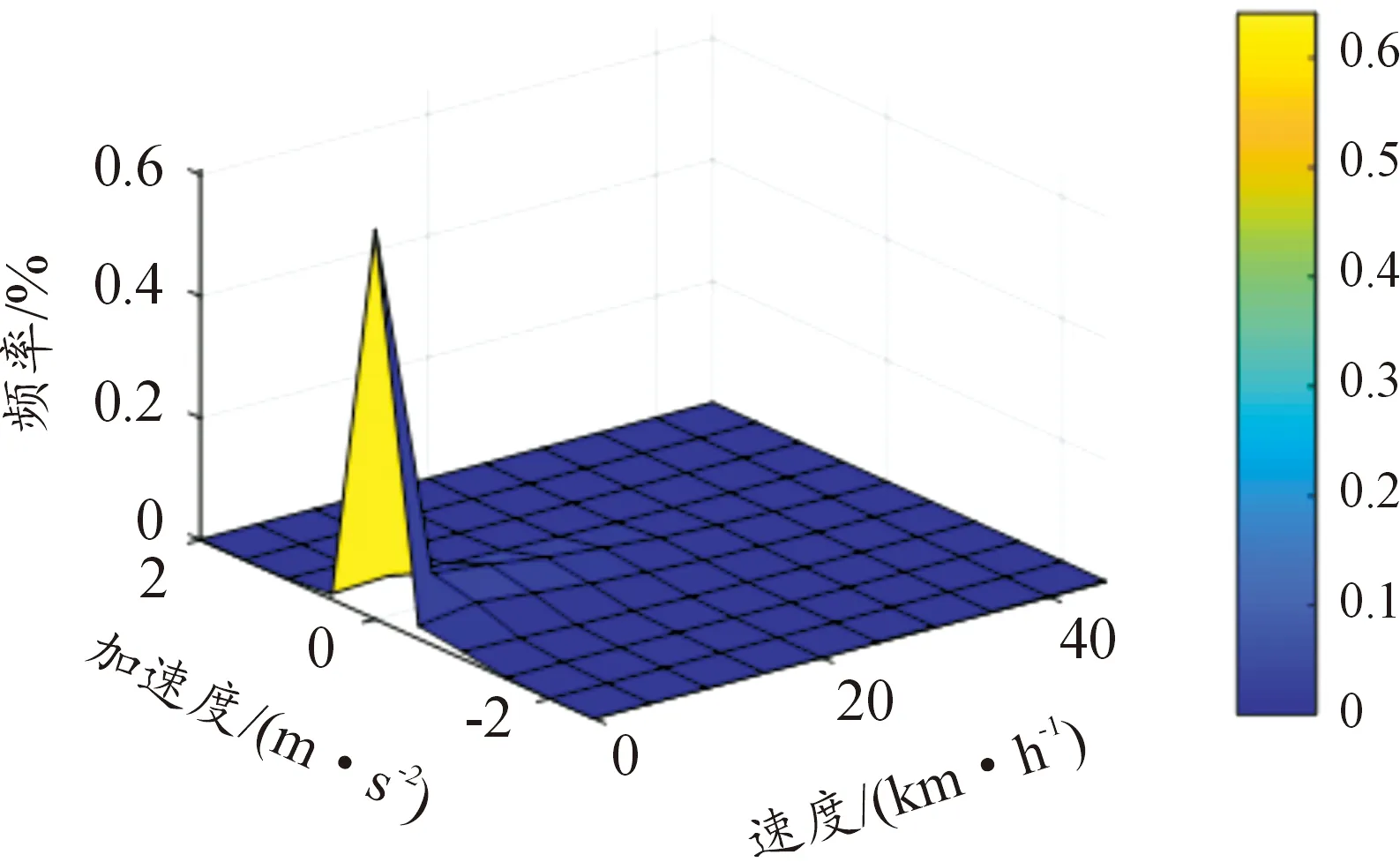
圖14 原始樣本數據速度加速度聯合分布

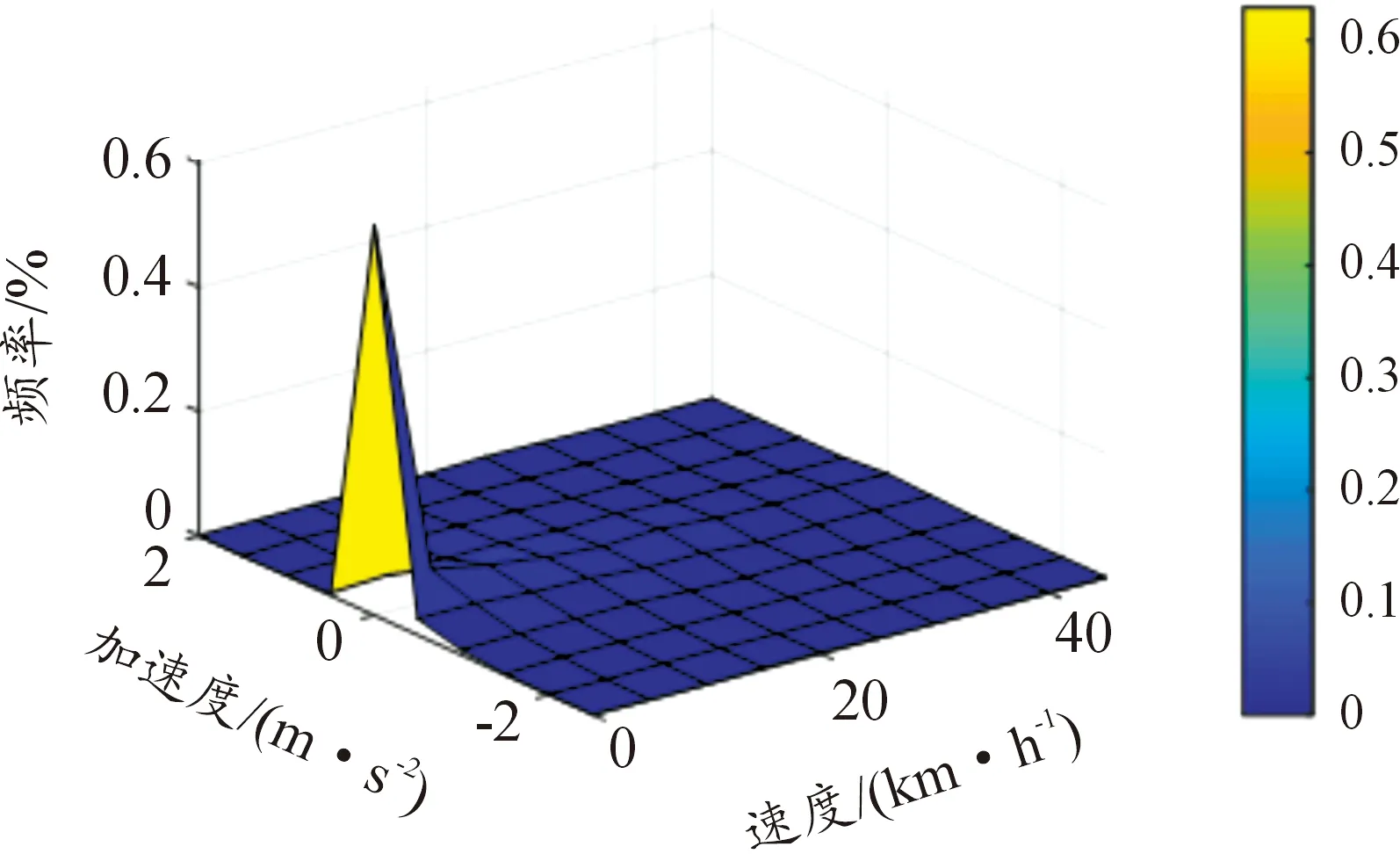
圖15 行駛工況速度加速度聯合分布

3.3 典型工況對比

由表10，通過比較成都市電動汽車行駛工況與歐洲行駛工況NEDC[10]、中國的乘用車CLTC-P工況[4]以及合肥[26]、西安[27]的電動汽車行駛工況的特征參數，成都市電動汽車行駛工況的平均速度,加速、減速、勻速、怠速時間比等存在顯著差異，成都市電動汽車行駛工況具體特征表現為：平均速度較低，怠速比例高、勻速比例低。

表10 國內外幾種循環工況特征參數

分析其原因：① 我國不同地區的交通狀況不盡相同，使得不同地區的汽車行駛工況存在差異; ② 電動汽車與燃油車在動力系統的差異導致了車輛行駛特征的不同，電動汽車由于電機的低速恒扭矩且電動響應迅速等特性，相比于燃油車，電動汽車的起步較快且起步時間更短。若直接采用中國乘用車CLTC-P或歐洲行駛工況NEDC進行電動汽車能耗測試，則不能準確的反映成都市電動汽車實際行駛特征。

4 結論

針對研究過程中的3 640 800條原始車速數據，剔除了GPS缺失、怠速異常等數據，引入滑動平均濾波濾除干擾信息，得到1 863 736條有效車速數據，提取8 599個運動學片段并選取了17個特征參數進行研究，得出結論如下：

1) 通過主成分分析對特征參數矩陣進行降維處理，采用輪廓系數和肘部法結合的方式確定聚類數目，結合粒子群算法優化K均值聚類中心，最終構建了時長為1 502 s、最高車速為58.4 km/h、總行程為6.723 km。

采用此方法所構建的行駛工況精度更高，與樣本數據庫特征參數相對誤差均在5%以下，平均相對誤差為2.28%。

2) 所構建的成都市電動汽車行駛工況與國內外城市循環工況比較發現差異較大，說明汽車行駛工況受特定地域的道路交通影響，采用燃油車行駛工況不適用于電動汽車的性能評估，后續有必要對電動汽車行駛工況構建展開研究。