考慮轉向意圖的分布式電驅動汽車橫擺穩定性控制
杜云雷,王先云,韓忠良,王淑芬,楊建森
(1.大連大學機械工程學院, 遼寧 大連 116622;2.中汽研(天津)汽車工程研究院有限公司, 天津 300300;3.中國汽車技術研究中心有限公司, 天津 300300)
0 引言
近年國家公布了中國智能汽車發展規劃,為實現高級別自動駕駛汽車落地,將純電動汽車作為主要研究對象[1]。其中分布式電驅動汽車擁有輪四輪獨立驅、制動和主動前、后輪轉向等冗余控制自由度,為車輛操縱穩定性控制提供了更多的可行性。因此,設計完善的控制系統改善車輛操縱穩定性、提高駕駛體驗已成為當前學術界的研究熱點。
近十幾年,車輛穩定性控制領域的研究已取得了長足進展[2]。Shi等[3]提出一種分數階PID控制器來產生期望的附加橫擺力矩,并采用二次規劃(QP)方法將附加橫擺力矩最優分配給單個車輪。Sun等[4]提出一種考慮電機效率的主動節能直接橫擺力矩控制方法,結果表明該控制方法在滿足相同轉彎需求的同時可有效降低能耗。李勝琴等[5]采用滑膜控制理論及罰函數法設計橫擺穩定性控制策略,降低了車輛失穩機率。SAA等[6]提出一種人工神經網絡控制器,估計車輛所需的直接橫擺力矩,結果表明該控制策略改善了車輛的橫向穩定性。Novellis等[7]提出了一種基于前饋和反饋相結合的直接橫擺力矩控制器,在靜態條件下不斷修正車輛的不足轉向度,在瞬態過程增大偏航阻尼使車輛保持穩定性。上述文獻的研究都取得了一定的控制效果,但沒有考慮駕駛員的操作意圖,將導致車輛的穩定區域減小。高振海等[8]結合駕駛員的行駛意圖設計ESP系統控制工況,提高了車輛的快速響應性能。張琳[9]模擬經驗駕駛員的操縱特性采用基于滑膜算法的TV控制,改善了車輛的穩定性。但此控制策略將穩定性因數調節到過度轉向和中性轉向,使駕駛員感到緊張,同時由于大多數乘用車表現為不足轉向,使該策略在車型匹配上也有一定的局限性。
盡管在諸多改善車輛操穩性能的研究中已經注意到了駕駛員因素的重要性,但將轉向意圖與不足轉向度充分結合實現減小駕駛負擔、改善操穩性能的研究尚不充分。因此,本文提出一種考慮駕駛員轉向意圖的橫擺穩定性控制策略。該控制策略通過識別駕駛員轉向意圖來匹配合理的穩定性因數,利用縱向力調節橫擺角速度,減輕側向力的負擔,從而能夠減小駕駛員的操作負荷,改善車輛操縱穩定性。
1 整車動力學模型
1.1 CarSim整車動力學模型
本文的被控平臺車采用CarSim中某C級車輛模型。在此模型基礎上,將驅動系統調整為四輪獨立驅動形式;并將懸架模型中的非簧載質量增加,以更好符合分布式電動汽車的載荷分布特性。匹配好的整車主要參數如表1所示。其中,在不同垂向載荷Fz下的輪胎模型特性擬合結果如圖1所示。
1.2 2DOF模型與CarSim對比驗證
為驗證二自由度(2DOF)簡化模型參數擬合結果,將其與CarSim模型進行仿真對比,方向盤轉角為正弦輸入,車速90 km/h,得到的仿真結果如圖2所示。

表1 整車主要參數

圖1 CarSim輪胎模型特性擬合曲線
由圖2可以看出,在上述工況下,經典2DOF模型[9]與CarSim被控車模型誤差較小,證明兩模型匹配較好。需要說明的是,誤差主要由于CarSim模型是高自由度非線性模型與實車更為相近,而經典2DOF模型是簡化后的線性模型,故二者的響應時間存在一定差別。
2 含駕駛員轉向意圖的2DOF
2.1 駕駛員轉向意圖分析
駕駛員的轉向操作是影響車輛穩定性的主要因素[10]。經驗駕駛員通過合理配合驅制動關系,可在出入彎道時使車輛保持穩定。在入彎時適當踩制動踏板,使車輛的載荷前移,增大前輪側向力以產生較大橫擺角速度,幫助車輛更好的入彎。出彎時適當踩油門踏板,使車輛的載荷后移,增大后輪側向力以產生較小的橫擺角速度,有利于車輛出彎。本文結合經驗駕駛員的操作特性,根據方向盤轉角信號識別出轉向意圖,然后調節穩定性因數Kt來模仿經驗駕駛員的操作特性,即在入彎時減小車輛的穩定性因數,在出彎時增大車輛的穩定性因數,從而達到幫助過彎并防止甩尾的效果。


圖3 駕駛員的轉向意圖分析曲線


(1)
其中:K為車輛原有穩定因數;C0與C1為穩態增益系數,影響Kt的幅值;τ0與τ1為時間常數,影響Kt的瞬態響應時間。
2.2 含駕駛員轉向意圖的2DOF
為完成控制期望模型的建立,將車輛系統簡化成線性兩輪模型,將懸架剛度和車身剛度產生的影響附加在輪胎剛度中。進而得到線性2自由度車輛動力學模型,如圖4所示。

圖4 2自由度車輛模型示意圖
由圖4的與牛頓運動定律可得出2DOF動力學公式(2)[11]。
(2)
其中:
(3)
將式(3)代入式(2)得到微分方程:
(4)
其中:K1為前輪側偏剛度;K2為后輪側偏剛度。
將式(4)中的橫擺角速度公式拉普拉斯變換后可得:

(5)
其中:
(6)
其中:m為整車質量;vx為車輛縱向速度;β為質心側偏角;γ為橫擺角速度;Fy1為前輪側向力;Fy2為后輪側向力;Iz為橫擺轉動慣量;a為車輛前軸與質心的距離;b為車輛后軸與質心的距離;α1為前輪側偏角;α2為后輪側偏角;δf為前輪轉角;L為軸距。
將上節式(1)中的Kt替換式(6)G0中的K得到:
(7)
再將式(7)代入式(5)得到含轉向意圖的橫擺角速度傳遞函數為:

(8)
考慮輪胎力飽和的影響,控制期望應滿足如下約束[12]:
(9)
2.3 控制期望驗證
為驗證含轉向意圖的2DOF期望模型的準確性,將其和普通2DOF模型對比。采用正弦停滯工況,通過分析對比橫擺角速度之間的關系調試穩定因數Kt的參數。最終通過仿真標定出模型參數值為:C0=0.000 1、C1=0.000 2、τ0=τ1=0.005。得到橫擺角速度如圖5所示。

圖5 正弦停滯工況下橫擺角速度曲線
當方向盤轉角增大時相當于車輛在入彎,當方向盤轉角減小時相當于車輛在出彎。由此結合圖5可知:與普通2DOF模型相比,含轉向意圖模型在車輛入彎時會產生更大的橫擺角速度,體現車輛穩定性因數減小的趨勢;在出彎時會產生較小的橫擺角速度,體現穩定性因數增大的趨勢;穩態時二者產生的橫擺角速度相等。因此含轉向意圖模型反映了經驗駕駛員在出入彎道時的駕駛特性。
3 基于轉向意圖的TVC策略
本文采用模型預測控制(MPC)來決策附加橫擺力矩ΔM,進而對上述控制期望進行跟隨,達到減小駕駛員操作負荷和改善車輛穩定性的目的。
3.1 MPC控制器設計
MPC的基本原理包括模型預測未來和實時滾動優化[13]。因此將式(4)中引入直接橫擺力矩作為控制輸入如下:
(10)
將式(10)表示成狀態空間形式可得:
(11)
其中:
將式(11)中的系數矩陣進行離散化處理,轉化關系如下:

(12)
其中:τs為采樣時間。
將式(11)改為增量式模型。
Δx(k+1)=AΔx(k)+BdΔd(k)+Buu(k)
y(k)=Cx(k)+y(k-1)
(13)
根據MPC的基本原理[14],設定預測時域為p,控制時域為m,且m≤p。由式(13)可得出系統未來p步的預測輸出為:
Yp(k+1|k)=SxΔx(k)+Iy(k)+
Sdd(k)+SuΔU(k)
(14)
其中:

由此可得出MPC算法的代價函數如下:
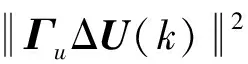
(15)

(16)
由MPC的滾動優化方式可取此時的附加橫擺力矩為:
ΔM=ΔMK
(17)
3.2 力矩分配方式
由于上述MPC求得的附加橫擺力矩ΔM不能直接作為控制的輸入量,所以在滿足縱的驅動力不變的前提下,需要對輪胎縱向力Fxi進行合理分配,產生橫擺力矩ΔM,具體關系如下:

(18)
其中:Fx為總的縱向驅動力。
為充分利用輪胎力,可將垂向載荷大的車輪分配相對大的縱向力,實現最優分配使車輛的穩定裕度提高。由此可以得到的目標函數如下[15]:
(19)
將式(18)與式(19)轉化為二次規劃形式其詳細推導過程見文獻[14]:
(20)
由式(20)可以求出四輪縱向力如下:
(21)
考慮輪胎力的飽和因素,因此縱向力應有如下約束:

(22)
由式(21)可得到力矩分配結果如下:
T=Ru1
(23)
4 仿真驗證
基于駕駛員轉向意圖的TVC策略系統如圖6所示,采用CarSim & Simulink聯合仿真的方法搭建驗證平臺,選用雙移線和角脈沖工況,分別以含轉向意圖模型作為控制期望的TVC策略、以普通2DOF模型作為控制期望的TVC策略和不加控制時進行對比仿真測試。在控制輸入的權重矩陣Γu中,其質心側偏角的權重系數設置為零。

圖6 基于駕駛員意圖的TVC策略系統
由于本文考慮轉向意圖的期望為橫擺角速度,而質心側偏角不涉及轉向意圖,故本策略通過跟隨期望橫擺角速度來提升操控性,同時預防失穩的發生。
4.1 雙移線工況
為驗證含轉向意圖的TVC策略在減小駕駛員負荷和改善車輛穩定性方面的有效性,選用雙移線工況開展仿真。目標車速vx=90 km/h,路面附著系數μ=0.85,得到的仿真結果如下。
從圖7可分析出,當駕駛員通過雙移線的過程中,不加控制時,方向盤轉角峰值為83°,采用普通2DOF為期望的TVC策略時,方向盤轉角峰值為71°,采用含轉向意圖的TVC策略時,方向盤轉角峰值為62°。結合圖8可以看出,采用含轉向意圖的TVC策略時,方向盤轉角變化率峰值也為最小。因此可說明:本控制策略通過識別駕駛員的轉向意圖調節車輛穩定性因數,以入彎減小出彎增大的原則,使駕駛員用較小的方向盤轉角就可產生期望的橫擺角速度完成過彎。進而實現在極限工況下有效的減輕駕駛員的操作負荷,提升了車輛的操縱性能。
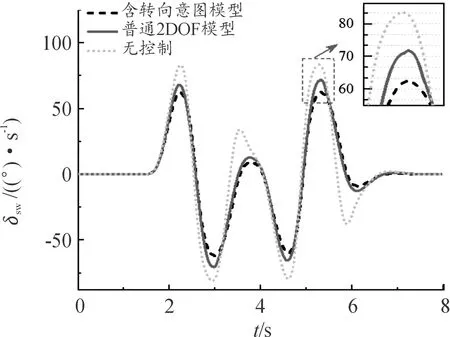
圖7 方向盤轉角曲線

圖8 方向盤轉角變化率曲線
從圖9可得出,本文提出的基于MPC算法的控制策略,對橫擺角速度的跟隨性很好,同時從圖11可以看出,本控制策略得到的質心側偏角相軌跡面積最小,表示車輛更趨于穩定。由此說明TVC策略,通過合理的分配驅制動產生的附加橫擺力矩可減輕側向力的負擔,從而使車輛在極限工況下有更好的穩定性。

圖9 雙移線工況下橫擺角速度曲線

圖10 雙移線工況下四輪轉矩曲線
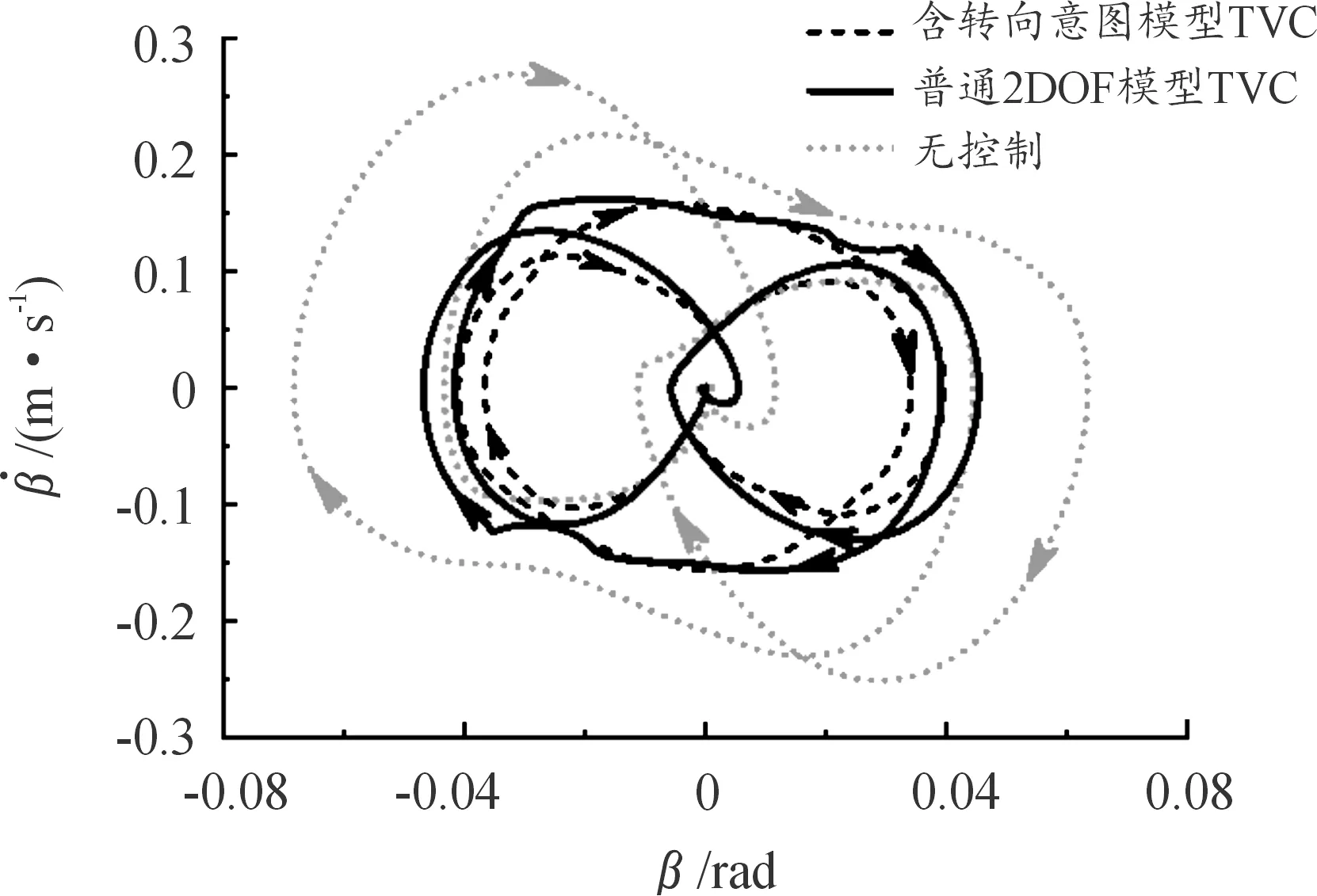
圖11 雙移線工況下質心側偏角相軌跡曲線
4.2 角脈沖工況
選用角脈沖工況驗證TVC策略的瞬態效果。目標車速vx=90 km/h,路面附著系數μ=0.85,得到的仿真結果如下。
從圖12可以看出在瞬態輸入情況下,TVC策略對橫擺角速度的跟隨性很好,產生的橫擺角速度最大,且響應更快。結合圖13可發現三者的相軌跡差別較小且均處于穩定區域內,由此可說明含轉向意圖的TVC策略在瞬態情況下表現更好。其原因在于縱向力可幫助側向力產生一定的橫擺角速度,使其瞬態響應更快。
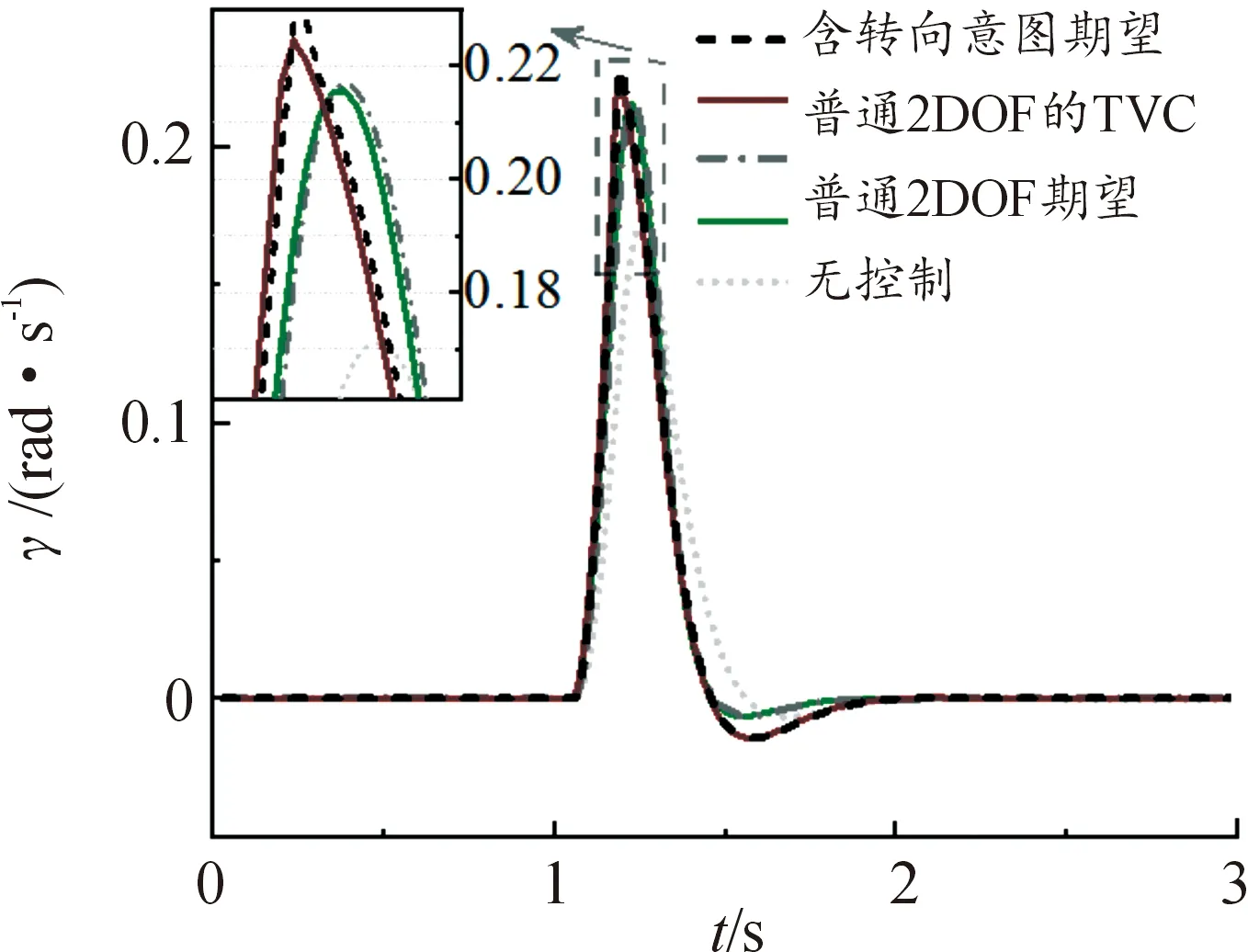
圖12 角脈沖工況下橫擺角速度曲線
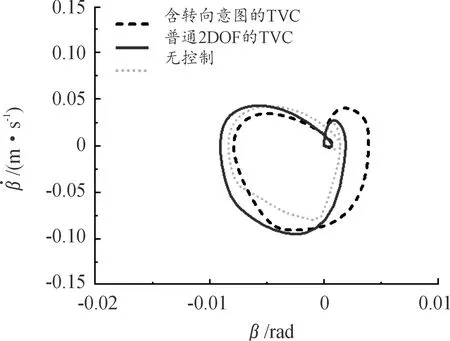
圖13 角脈沖工況下質心側偏角相軌跡曲線

圖14 角脈沖工況下附加橫擺力矩曲線
5 結論
為改善分布式驅動電動汽車在極限工況下的操縱穩定性,提出基于MPC算法的考慮轉向意圖TVC策略。首先,在分析經驗駕駛員操作特性的基礎上,制定了含轉向意圖的控制期望,當車輛入彎時減小穩定性因數,當車輛出彎時增大穩定性因數。然后,采用MPC方法和QP算法,決策出基于最優分配的四輪轉矩作為控制量來保持車輛對期望的跟隨。利用縱向力產生橫擺角速度的能力來減小側向力的負擔,提高車輛的穩定性。最后,采用CarSim&Simulink聯合仿真方法,對所提控制策略進行仿真分析,驗證了此控制方法在極限工況下可有效減小駕駛員的操縱負荷,提高車輛的穩定性。

