一種新的廣義對(duì)數(shù)正態(tài)分布點(diǎn)估計(jì)方法
溫錄亮,陳平炎
(1.佛山科學(xué)技術(shù)學(xué)院, 廣東 佛山 528225;2.暨南大學(xué), 廣州 510632)
0 引言
基于正態(tài)分布的推廣和應(yīng)用一直是統(tǒng)計(jì)學(xué)領(lǐng)域的熱點(diǎn)研究問(wèn)題,如2021年,魏正元等[1]提出了離散alpha偏正態(tài)分布,并分析了其性質(zhì)和參數(shù)估計(jì)問(wèn)題。對(duì)正態(tài)分布進(jìn)行拓展,可以得到對(duì)數(shù)正態(tài)分布,目前對(duì)數(shù)正態(tài)分布已廣泛應(yīng)用于生命科學(xué)的不同領(lǐng)域,包括生物學(xué)、生存分析以及金融和風(fēng)險(xiǎn)分析等[2-3]。2005年,Nadarajah[4]提出并研究了廣義正態(tài)分布的相關(guān)性質(zhì),并討論了極大似然估計(jì),給出了信息矩陣。在此研究基礎(chǔ)上,2009年,Martín等[5]提出了廣義對(duì)數(shù)正態(tài)分布,利用貝葉斯方法進(jìn)行參數(shù)估計(jì),并應(yīng)用于分析生命周期數(shù)據(jù)。2012年,Singh等[6]對(duì)廣義對(duì)數(shù)正態(tài)分布的極大似然估計(jì)和貝葉斯估計(jì)進(jìn)行了對(duì)比研究。2013年,Toulias等[7]和Kleiber[8]討論了廣義對(duì)數(shù)正態(tài)分布不同條件下的矩求解問(wèn)題。2017年,Li等[9]提出使用Jeffreys先驗(yàn),比較了廣義對(duì)數(shù)正態(tài)分布在已知先驗(yàn)和極大值條件下的貝葉斯估計(jì)性能。2020年,Tomazella等[10]提出了一種新的貝葉斯方法,估計(jì)了廣義對(duì)數(shù)正態(tài)分布的參數(shù)并應(yīng)用于生存數(shù)據(jù)分析。綜上所述,相關(guān)學(xué)者針對(duì)廣義對(duì)數(shù)正態(tài)分布的參數(shù)估計(jì),主要采用極大似然估計(jì)或貝葉斯估計(jì)方法。為此,提出廣義對(duì)數(shù)正態(tài)分布形狀參數(shù)一種新的強(qiáng)相合的點(diǎn)估計(jì)量,并和極大似然估計(jì)、貝葉斯估計(jì)結(jié)果進(jìn)行對(duì)比,評(píng)估新提出的點(diǎn)估計(jì)方法的性能。
在內(nèi)容的編排上,第1節(jié)給出了廣義對(duì)數(shù)正態(tài)分布的定義和期望方差;第2節(jié)將提出廣義對(duì)數(shù)正態(tài)分布形狀參數(shù)υ和σ的一種新的點(diǎn)估計(jì)量,給出具體的證明過(guò)程和逆變換抽樣方法;第3節(jié)進(jìn)行數(shù)值模擬,驗(yàn)證第2節(jié)定理的結(jié)論;第4節(jié)將提出的點(diǎn)估計(jì)和極大似然估計(jì)、貝葉斯估計(jì)結(jié)果進(jìn)行對(duì)比,評(píng)估點(diǎn)估計(jì)性能;第5節(jié)給出結(jié)論。
1 廣義對(duì)數(shù)正態(tài)分布
如果一個(gè)隨機(jī)變量X服從廣義對(duì)數(shù)正態(tài)分布,則其概率密度函數(shù)可以寫(xiě)為:
(1)


圖1 廣義對(duì)數(shù)正態(tài)分布的概率密度函數(shù)曲線(xiàn)(μ=0,σ=1)
參考文獻(xiàn)[8,11],當(dāng)υ>1時(shí),可以推導(dǎo)出廣義對(duì)數(shù)正態(tài)分布k階原點(diǎn)矩。
命題1設(shè)隨機(jī)變量X的概率密度函數(shù)為式(1),則X的k階原點(diǎn)矩為:
(2)
證明根據(jù)計(jì)算公式,有:

將式(1)代入,得出:






從而可以寫(xiě)出廣義對(duì)數(shù)正態(tài)分布的期望和方差為:
利用矩估計(jì)時(shí)要注意,以上是當(dāng)υ>1時(shí)的k階原點(diǎn)矩。當(dāng)υ<1時(shí),k階原點(diǎn)矩不存在;當(dāng)υ=1時(shí),由上述推導(dǎo)可知,當(dāng)且僅當(dāng)kσ<1時(shí)存在k階原點(diǎn)矩。
2 點(diǎn)估計(jì)及逆變換抽樣
本節(jié)通過(guò)來(lái)自廣義對(duì)數(shù)正態(tài)分布總體樣本的極值來(lái)估計(jì)形狀參數(shù),并證明此估計(jì)量是強(qiáng)相合的。具體地,設(shè)總體X服從廣義對(duì)數(shù)正態(tài)分布,即其概率密度函數(shù)為式(1),X1,X2,…,Xn為來(lái)自總體X容量為n的樣本,則形狀參數(shù)υ的估計(jì)量為:
若υ已知,則σ的估計(jì)量為:
下面的結(jié)論表明這2個(gè)估計(jì)量都是強(qiáng)相合的。
定理1設(shè)隨機(jī)變量X服從廣義對(duì)數(shù)正態(tài)分布,X1,X2,…,Xn為來(lái)自總體X容量為n的樣本,則:

(3)
下面給出定理1的證明,先介紹一些記號(hào)和必要的引理。
設(shè){An,n≥1}是一個(gè)事件序列,參考文獻(xiàn)[12],記

表示事件序列{An,n≥1}發(fā)生無(wú)窮多次。
運(yùn)用翻轉(zhuǎn)課堂是一種培養(yǎng)學(xué)生自主性的有效方式。“翻轉(zhuǎn)教室”這一名詞最早起源于美國(guó),其具體形式為:首先學(xué)生在課外通過(guò)網(wǎng)絡(luò)平臺(tái),觀看學(xué)習(xí)老師做的教學(xué)視頻,然后再由教師在課堂上進(jìn)行測(cè)試,并討論了課前記憶的知識(shí),最后幫學(xué)生們將知識(shí)轉(zhuǎn)為內(nèi)化[3]。顯而易見(jiàn),將知識(shí)共享并實(shí)現(xiàn)內(nèi)化是老師和學(xué)生在課堂上互相協(xié)助實(shí)現(xiàn)的。“翻轉(zhuǎn)課堂”的特點(diǎn)十分明顯,學(xué)生和老師的角色互換的傳統(tǒng)教學(xué)過(guò)程是教師集中作業(yè),學(xué)生的學(xué)習(xí)任務(wù)是事先不可知的。但在“翻轉(zhuǎn)課堂”教學(xué)形式中,學(xué)生可以提前學(xué)習(xí)知識(shí),之后在課堂上教師和學(xué)生共同學(xué)習(xí)的一種新穎方式。這樣更加注重學(xué)生的自主性及在課堂上的研究,討論與同伴以及老師的協(xié)作、交流以及反思。
下面的引理1可參考文獻(xiàn)[13],引理2可參考文獻(xiàn)[4]。

(4)
引理2如果隨機(jī)變量X服從廣義對(duì)數(shù)正態(tài)分布,可以得到:
(5)
命題2設(shè){X,Xn,n≥1}是獨(dú)立且恒等分布的序列,假設(shè)X服從廣義對(duì)數(shù)正態(tài)分布,則可以得到:
(6)
證明不失一般性,可以假設(shè)μ=0,首先證明:
等價(jià)于證明:
對(duì)任意的ε>0,通過(guò)引理1可以得到:
P{logXn≥(1+ε)1/υσ(logn)1/υi.o.}=0
根據(jù)Borel-Cantelli引理,要證明上式,只需證明:
通過(guò)引理2,可以得到:
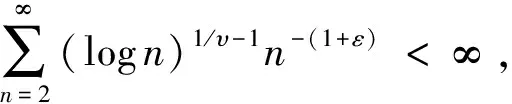


根據(jù)Borel-Cantelli引理,要證明上式,只要證明對(duì)任意的ε>0,有:
已知對(duì)任意的x>0,有1-x [1-P{logX≥(1-ε)1/υσ(logn)1/υ}]n< e-nP{log X≥(1-ε)1/υσ(log n)1/υ} 通過(guò)引理2可以得到: nP{logX≥(1-ε)1/υσ(logn)1/υ}~ 上式中的不等式對(duì)于足夠大的n成立。 綜上可以得到: 定理1的證明由上面推導(dǎo)得知當(dāng) 因此: 為了對(duì)定理1進(jìn)行數(shù)值模擬,需要產(chǎn)生相應(yīng)的隨機(jī)數(shù)。下面的逆變換抽樣方法借鑒了文獻(xiàn)[5,14]的思想方法。 設(shè)X、U、V是隨機(jī)變量,抽樣算法流程為: 步驟1設(shè)U~Γ(1+1/υ,1),產(chǎn)生隨機(jī)數(shù); 步驟2設(shè)V~Uniform (-1,1),產(chǎn)生隨機(jī)數(shù); 步驟3令X=exp(σU1/υV+μ),可以得到服從廣義對(duì)數(shù)正態(tài)分布的隨機(jī)數(shù)。 利用以上算法流程,選取500個(gè)隨機(jī)數(shù),可以畫(huà)出抽樣概率密度曲線(xiàn)和真實(shí)概率密度曲線(xiàn)的對(duì)比圖。通過(guò)圖2可以發(fā)現(xiàn),υ取不同值時(shí)的抽樣概率密度曲線(xiàn)和真實(shí)概率密度曲線(xiàn)重合度都很高,說(shuō)明通過(guò)命題3提出的逆變換方法對(duì)廣義對(duì)數(shù)正態(tài)分布進(jìn)行抽樣,效果是理想的。 圖2 廣義對(duì)數(shù)正態(tài)分布的抽樣概率密度曲線(xiàn)和真實(shí)概率密度曲線(xiàn)(μ=0,σ=1) 本節(jié)進(jìn)行數(shù)值模擬,評(píng)估廣義對(duì)數(shù)正態(tài)分布的點(diǎn)估計(jì)性能。首先給出偏度和均方誤差的公式: (7) 表1 關(guān)于廣義對(duì)數(shù)正態(tài)分布參數(shù)υ的點(diǎn)估計(jì)結(jié)果 圖3 關(guān)于廣義對(duì)數(shù)正態(tài)分布參數(shù)υ的點(diǎn)估計(jì)量收斂效果圖 nσ=1σ=2σ=3估計(jì)值偏度均方誤差901.340 82.711 54.051 20.340 80.711 51.051 20.106 30.526 11.373 2估計(jì)值偏度均方誤差9001.179 92.357 43.520 40.179 90.357 40.520 40.045 90.038 40.261 8 nσ=1σ=2σ=3估計(jì)值偏度均方誤差9 0001.065 32.131 53.198 10.065 30.131 50.198 10.007 71E-40.058 4估計(jì)值偏度均方誤差90 0000.980 41.980 22.966 00.019 60.019 80.034 02E-40.001 20.020 6 圖4 關(guān)于廣義對(duì)數(shù)正態(tài)分布參數(shù)σ的點(diǎn)估計(jì)量收斂效果圖 第3節(jié)對(duì)定理1的結(jié)論進(jìn)行了數(shù)值模擬驗(yàn)證,本節(jié)對(duì)點(diǎn)估計(jì)和極大似然估計(jì)、貝葉斯估計(jì)的結(jié)果進(jìn)行對(duì)比。固定μ=0,σ=1,取υ=2,3,利用點(diǎn)估計(jì)方法仿真實(shí)驗(yàn)重復(fù)進(jìn)行100次,求平均值得到估計(jì)結(jié)果,并和Li等[9]提出的極大似然估計(jì)、貝葉斯估計(jì)結(jié)果進(jìn)行對(duì)比,如表3和表4所示。 表3 關(guān)于參數(shù)υ=2的點(diǎn)估計(jì)和極大似然估計(jì)、貝葉斯估計(jì)的結(jié)果 表4 關(guān)于參數(shù)υ=3的點(diǎn)估計(jì)和極大似然估計(jì)、貝葉斯估計(jì)的結(jié)果 通過(guò)表3和表4可以發(fā)現(xiàn),針對(duì)參數(shù)υ,在樣本量分別為n=25,50,100的情況下,利用提出的點(diǎn)估計(jì)方法,得出參數(shù)估計(jì)結(jié)果的偏度值明顯大于極大似然估計(jì)和貝葉斯估計(jì)得出的結(jié)果。所以說(shuō),如果樣本量較小,利用極大似然估計(jì)或貝葉斯估計(jì)是合適的,而利用點(diǎn)估計(jì)則會(huì)產(chǎn)生較大誤差。如果樣本量較大(如超過(guò)10 000),建議考慮選用點(diǎn)估計(jì)方法。相對(duì)于其他估計(jì)方法,提出的這種新點(diǎn)估計(jì)方法更加簡(jiǎn)單易算。 提出了廣義對(duì)數(shù)正態(tài)分布形狀參數(shù)υ和σ的一種新的點(diǎn)估計(jì)量,給出了推導(dǎo)證明過(guò)程,利用逆變換抽樣方法進(jìn)行數(shù)值模擬,可以看到隨著樣本量n的增大,估計(jì)值越來(lái)越收斂于真實(shí)值,和定理1的結(jié)論一致。和廣義對(duì)數(shù)正態(tài)分布的極大似然估計(jì)、貝葉斯估計(jì)結(jié)果進(jìn)行對(duì)比,發(fā)現(xiàn)這種新的點(diǎn)估計(jì)方法不適用小樣本估計(jì),而適用于大樣本估計(jì),在進(jìn)行相關(guān)大數(shù)據(jù)分布模型參數(shù)估計(jì)時(shí),具有推廣應(yīng)用價(jià)值。




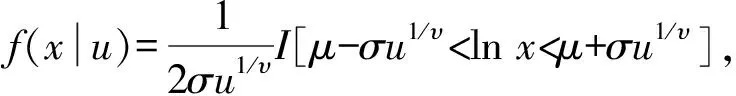

3 數(shù)值模擬











4 參數(shù)估計(jì)效果對(duì)比


5 結(jié)論

