具有無限馬爾可夫二維Roesser系統(tǒng)的模糊H∞狀態(tài)反饋控制

葉志勇，嚴(yán) 芳，羅小玉，何 鑫，趙紅霞

(1.重慶理工大學(xué) 理學(xué)院， 重慶 400054；2.重慶人文科技學(xué)院 機電與信息工程學(xué)院， 重慶 401524)

0 引言

眾所周知，馬爾可夫跳躍系統(tǒng)在模擬突變結(jié)構(gòu)和參數(shù)變化方面具有一定的研究意義。值得注意的是，現(xiàn)有的大多成果都是在有限狀態(tài)空間馬爾可夫鏈條件下進(jìn)行的。近年來，具有無限狀態(tài)空間馬爾可夫跳系統(tǒng)引起了學(xué)者們的密切關(guān)注[5]，人們已經(jīng)認(rèn)識到，有限馬爾可夫跳系統(tǒng)和無限馬爾可夫跳系統(tǒng)的性能存在本質(zhì)的區(qū)別。文獻(xiàn)[6]討論了對于平穩(wěn)的有限馬爾可夫跳系統(tǒng)，隨機穩(wěn)定性等價于漸近均方穩(wěn)定性，但在無限狀態(tài)空間馬爾可夫鏈情況下則并非如此。文獻(xiàn)[7]研究了帶無限狀態(tài)馬爾可夫鏈的離散時間不確定時滯系統(tǒng)的穩(wěn)定性，討論了系統(tǒng)漸近均方穩(wěn)定性、隨機穩(wěn)定性、均方指數(shù)穩(wěn)定性等之間的關(guān)系。

一般來說，T-S模糊模型的優(yōu)點是通過對局部線性系統(tǒng)模型的“混合”，來逼近任意光滑非線性函數(shù)，從而使線性控制系統(tǒng)理論有助于解決非線性問題。文獻(xiàn)[8]研究了基于Fornasini-Marchesini (FM)局部狀態(tài)空間模型建立二維離散模糊系統(tǒng)模型的穩(wěn)定性分析問題。文獻(xiàn)[9]研究了離散時間非線性二維Roesser模型系統(tǒng)的鎮(zhèn)定問題。文獻(xiàn)[10]考慮了第二FM模型下基于觀測器的二維T-S模糊系統(tǒng)的H∞控制器設(shè)計。文獻(xiàn)[11-12]解決了Roesser模型的控制問題。文獻(xiàn)[13]研究了用Roesser模型描述的T-S模糊系統(tǒng)的耗散性分析和控制器設(shè)計問題。文獻(xiàn)[14]針對二維離散切換系統(tǒng)的H∞魯棒控制器設(shè)計問題，采用具有多面體不確定性的Roesser模型來描述。文獻(xiàn)[15]利用T-S模糊模型方法解決了一類受規(guī)定干擾衰減水平影響的非線性網(wǎng)絡(luò)控制系統(tǒng)的事件觸發(fā)濾波問題。

目前，帶有無限狀態(tài)空間馬爾可夫鏈的二維Roesser T-S模糊模型系統(tǒng)的漸近均方穩(wěn)定的H∞控制問題仍然是一個非常有趣且具有一定挑戰(zhàn)性的問題。也很少有工作去處理這個問題，這主要是因為二維Roesser系統(tǒng)、無限狀態(tài)空間馬爾可夫鏈和T-S模糊模型的性質(zhì)所引起的數(shù)學(xué)復(fù)雜性。因此，帶有無限狀態(tài)空間馬爾可夫鏈的二維Roesser T-S模糊模型系統(tǒng)的漸近均方穩(wěn)定的H∞控制問題的成果并不多，這推動了筆者的研究。

主要研究了對帶有無限狀態(tài)空間馬爾可夫鏈的二維Roesser T-S模糊模型系統(tǒng)的漸近均方穩(wěn)定的H∞控制問題。首先介紹了Roesser模糊模型系統(tǒng)的預(yù)備知識，通過構(gòu)造Lyapunov函數(shù)以及線性矩陣不等式方法證明了帶無限狀態(tài)空間馬爾可夫鏈的二維Roesser T-S模糊模型系統(tǒng)的漸近均方穩(wěn)定性和H∞控制問題，并用一個特例驗證其有效性和實用性。

1 基礎(chǔ)知識和模型建立

1.1 符號說明

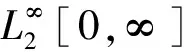
1.2 模型描述

在(M,F,P)空間上考慮一個二維離散時間T-S模糊Roesser模型系統(tǒng)如下：

規(guī)則kIfθ1(i,j) isMk,1，andθ2(i,j) isMk,2,…,θg(i,j) isMk,g，then

(1)

這里θ(i,j)=[θ1(i,j),θ2(i,j),…,θg(i,j)]是前提變量；Mk,l對l=1,…,g是模糊集，xh(i,j)∈Rnh是水平方向狀態(tài)，xv(i,j)∈Rnv是垂直方向狀態(tài)，u(i,j)∈Rnu是控制輸入，ω(i,j)∈Rnω是外部干擾，y(i,j)∈Rny是可測輸出，r是模糊規(guī)則數(shù)。其中

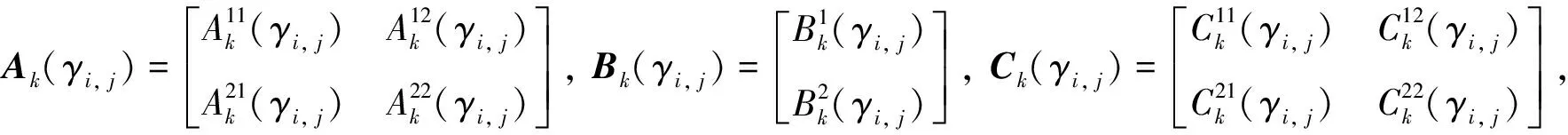
是已知相應(yīng)維數(shù)的實值矩陣，并且他們都是馬爾可夫鏈γi, j的函數(shù)。

γi, j在無限可數(shù)集K1={1,2，…}中取值，轉(zhuǎn)移概率矩陣Θ1=(Λpq)，Λpq形式如下：

Pr{γi+1, j=q|γi, j=p}=Pr{γi, j+1=q|γi, j=p}=Λpq

(2)

根據(jù)概率論，Λpq滿足如下條件：

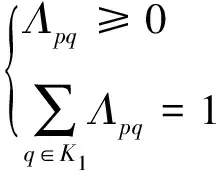
(3)

對?p,q∈K1。系統(tǒng)(1)的邊界條件(X0,Γ0)定義如下：

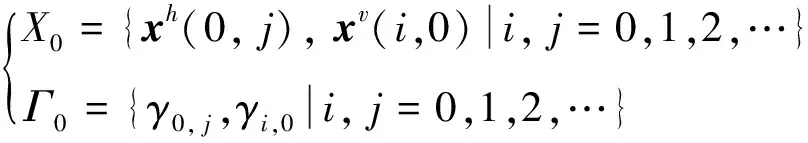
(4)

同時，將零邊界條件定義為：

xh(0,j)=0,xv(i,0)=0,i,j=0,1,2,…

進(jìn)一步在X0上作出如下假設(shè)。

假設(shè)1假設(shè)X0滿足下列條件：

(5)

這里E{·}表示數(shù)學(xué)期望，|·|表示歐式范數(shù)。

模糊集函數(shù)定義如下：

(6)

這里μk,l(θl(i,j))是在模糊規(guī)則數(shù)k上θ(i,j)的隸屬度。通過定義有：

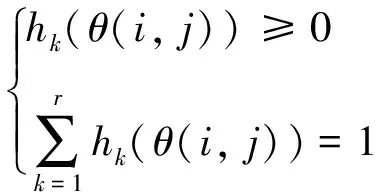
基于模糊規(guī)則，T-S模糊Roesser模型可以推斷如下：

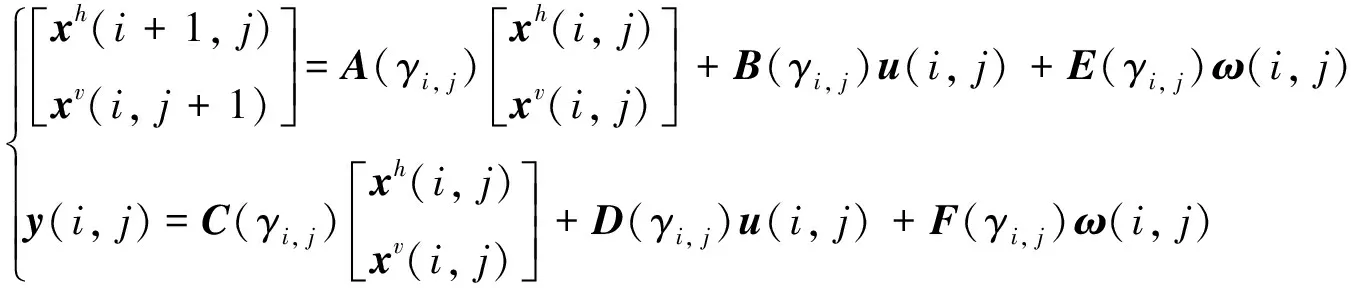
(7)

其中：

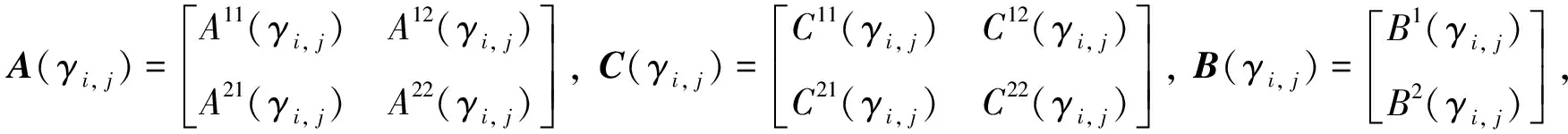
本節(jié)采用了狀態(tài)反饋控制中常用的假設(shè)，假設(shè)γi, j的精確值難以獲得，設(shè)計狀態(tài)反饋控制器如下：

(8)

這里K(ηi, j)表示控制增益，它依賴于參數(shù)ηi, j∈K2(K2={1,2,…})，ηi, j是變量控制的模式，同時它的條件概率Λps可以由γi, j得到，即：

Pr{ηi, j=s|γi, j=p}=Λps

(9)

Θ2=(Λps)為條件概率矩陣，同樣滿足：

將γi, j、γi+1, j(γi, j+1)、ηi, j簡記為p、q、s，如A(ηi, j)簡記為Aq。

把式(8)代入式(7)得到閉環(huán)動態(tài)系統(tǒng)如下:

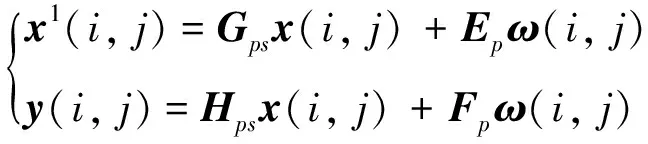
(10)

其中：

Gps=Ap+BpKs,Hps=Cp+DpKs

注:本節(jié)得到的閉環(huán)系統(tǒng)形式上與文獻(xiàn)[12]的閉環(huán)系統(tǒng)相似，是在此基礎(chǔ)上向T-S模糊模型、無限狀態(tài)空間的馬爾可夫鏈進(jìn)行的推廣。

為了進(jìn)一步研究對帶有無限狀態(tài)空間馬爾可夫鏈的二維Roesser T-S模糊模型系統(tǒng)的漸近均方穩(wěn)定的H∞控制問題，給出如下定義。

定義1當(dāng)閉環(huán)二維系統(tǒng)(10)中外部擾動輸入ω(i,j)=0時，如果對任何邊界條件(X0,Γ0)滿足如下條件：

(11)

則閉環(huán)系統(tǒng)(10)被稱為漸近均方穩(wěn)定。

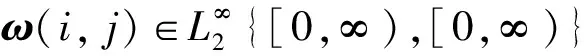
(12)

則閉環(huán)系統(tǒng)(10)有H∞性能指標(biāo)μ。

2 主要結(jié)論

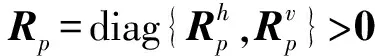
(13)

(14)

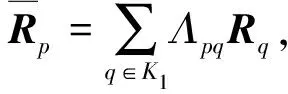
證明構(gòu)造李亞普諾夫函數(shù)如下：

V(i,j)=xT(i,j)Rpx(i,j)

定義：

ΔV(i,j)=x1T(i,j)Rqx1(i,j)-xT(i,j)Rpx(i,j)

(15)

根據(jù)狀態(tài)方程(10)，當(dāng)ω(i,j)≡0時，很容易得到：

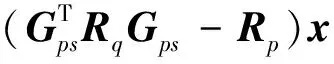
(16)

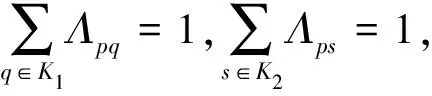
(17)

通過舒爾補引理，從式(14)得到：

(18)

結(jié)合式(17)和式(18)，可得：

(19)

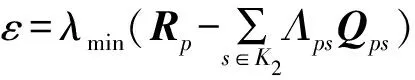
(20)

這里m1,m2是正整數(shù)。

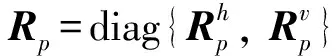
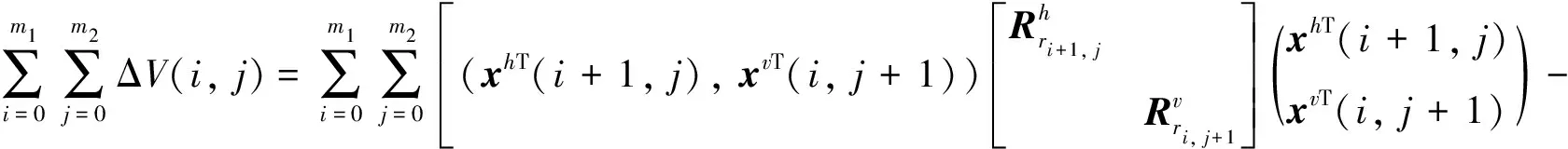
(21)

通過式(20)和式(21)可以推得：

(22)

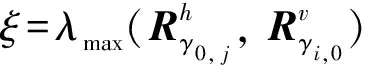
(23)

由假設(shè)1中的式(5)，有

(24)

則式(11)滿足，故閉環(huán)系統(tǒng)(10)漸近均方穩(wěn)定。得證。

進(jìn)一步地，討論基于零邊界條件下的H∞性能指標(biāo)。

記

則式(14)等價于如下矩陣：

(25)

通過舒爾補定理，等價矩陣(25)可以等價于如下不等式：

(26)

通過閉環(huán)系統(tǒng)(10)，得到：

(27)

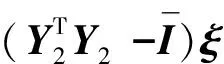
(28)

(29)

結(jié)合式(27)和式(28)，可得：

E{yT(i,j)y(i,j)-μ2ωT(i,j)ω(i,j)+ΔV(i,j)}=

(30)

只要條件(13)(26)成立，即得到J<0，可以推得：

(31)

在零邊界條件下，又由式(21)(29)(30)，得到：

(32)

綜上所述，對無限狀態(tài)空間馬爾可夫鏈的模糊Roesser模型，根據(jù)定義2，則式(12)滿足，故定理1得證。即最終得到了關(guān)于無限狀態(tài)空間馬爾可夫跳的模糊Roesser模型系統(tǒng)在假設(shè)1條件下的漸近均方穩(wěn)定和H∞控制的充分條件。

接下來，給出一個實例的仿真模擬來驗證其定理的有效性以及實用性。

3 仿真模擬

在本節(jié)中，基于文獻(xiàn)[16-17]將提供一個實例來說明所提出方法的有效性。在現(xiàn)實世界中，有些氣體吸收、水流加熱的動力學(xué)過程和空氣干燥可以如下公式表示：

b(γi, j)u(x,t)+e(γi, j)ω(x,t)

(33)

其中：f(x,t)是關(guān)于空間x∈[0,xf]和時間t∈[0,∞]的未知函數(shù)；a0(γi, j),a1(γi, j),a2(γi, j),a3(γi, j),b(γi, j),e(γi, j)是關(guān)于γi, j的函數(shù)；ω(x,t)是輸入擾動，u(x,t)是控制輸入。定義：

(34)

則微分方程(33)可轉(zhuǎn)化為以下二維狀態(tài)空間模型：

(35)

為了得到非線性系統(tǒng)的二維T-S模糊模型，考慮以下2個規(guī)則：

規(guī)則1If sin2(xv(x,t)) is about 0，then

(36)

規(guī)則2If sin2(xv(x,t)) is about 1，then

(37)

二維T-S模糊系統(tǒng)的隸屬函數(shù)是：

h1=cos2(xv(x,t)),h2=sin2(xv(x,t))

接下來，將上述T-S模糊系統(tǒng)離散化為采樣時間T1和T2，對應(yīng)于變量x和t。因此，帶無限馬可夫離散二維模糊系統(tǒng)由下式給出：

規(guī)則1If sin2(xv(x,t)) is about 0，then

(38)

規(guī)則2If sin2(xv(x,t)) is about 1，then

(39)

取T1=T2=0.1,a0(γi, j)=4,a1(γi, j)=-8,a2(γi, j)=-8以及b(γi, j)=-4,e(γi, j)=-4，得到系統(tǒng)相對應(yīng)的參數(shù)矩陣如下：

為了研究系統(tǒng)(1)的H∞控制問題，令式(1)中相應(yīng)的參數(shù)矩陣為：

其中轉(zhuǎn)移概率矩陣Θ1=(Λpq),Θ2=(Λps)為：

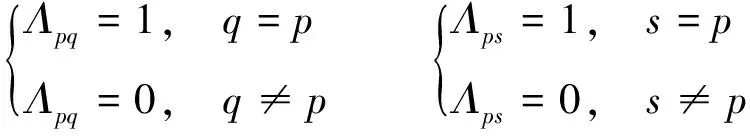
得到式(8)中反饋控制的反饋增益矩陣為：

利用Matlab對系統(tǒng)進(jìn)行模擬，模擬結(jié)果如圖1—3所示。模擬結(jié)果表明H∞控制中參數(shù)的最小值為u2=4。

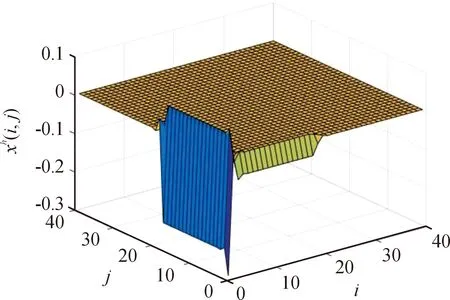
圖1 有控制輸入的水平狀態(tài)

由圖1和圖2可以看出，二維系統(tǒng)水平方向與垂直方向一開始波動比較大，但在一段時間后都漸近的逼近于零。因此證明了定理1。

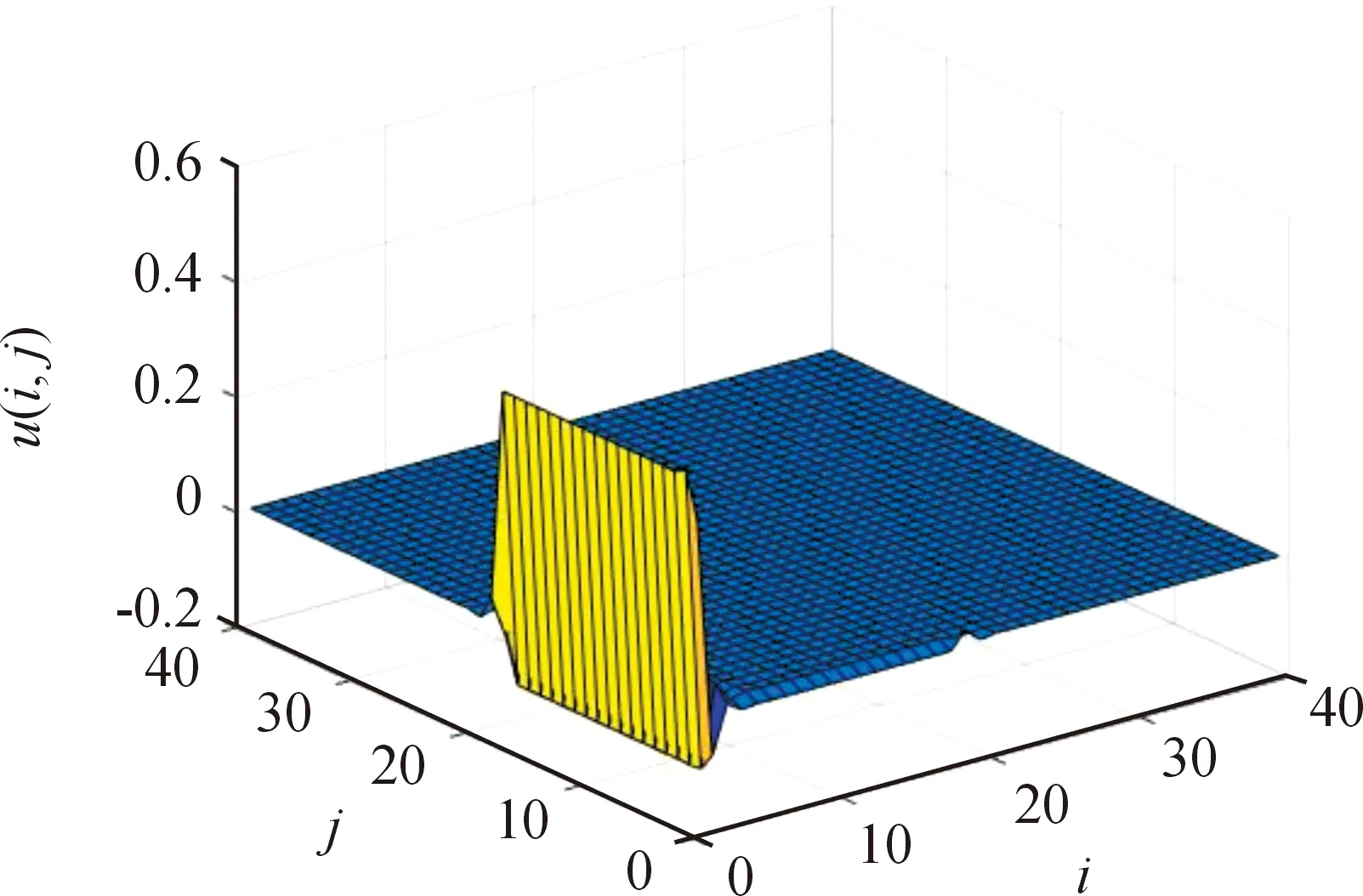
圖3 控制輸入圖

4 結(jié)論

目前的研究中，通常都是對二維Roesser模型H∞控制的研究；但帶有無限狀態(tài)空間馬爾可夫鏈的二維Roesser T-S模糊模型系統(tǒng)的漸近均方穩(wěn)定的H∞控制問題仍然是一個非常有趣和具有挑戰(zhàn)性的問題。基于T-S模糊模型，研究了一類離散時間無限狀態(tài)空間馬爾可夫跳二維Roesser模型系統(tǒng)的漸近均方穩(wěn)定性與H∞控制，并且通過構(gòu)建李雅普諾夫函數(shù)，利用線性矩陣不等式給出了證明。利用Matlab模擬出的結(jié)果表明H∞控制中參數(shù)的最小值為u2=4，驗證了理論的有效性和實用性。