多元非線性數學模型在碳纖維紙拉伸強度預測中的應用

孟建梅，王曉麗

（1.晉中職業技術學院，山西 晉中 030600；2.晉中學院，山西 晉中 030619）

0 引言

近年來，世界各國都在積極開發并應用新型清潔能源，目前燃料電池作為第四代發電技術，單位重量輸出的電能大、功率大，在軍用和民用等領域均具有較大的應用前景，故進行相關課題的開發和研究非常重要。碳纖維紙是燃料電池中的重要組成部分之一，作為燃料電池氣體擴散層的基底材料發揮重要作用［1］，直接關系到燃料電池燃料的利用率，碳纖維紙的拉伸強度關系到氣體擴散層中膜電極安裝的穩定性，關系到電池使用壽命［2］。基于此，對碳纖維紙拉伸強度進行預測具有重要的現實意義。

目前我國部分學者已經獲得一定的研究成果，文獻［3］中建立了高溫環境下碳纖維增強聚丙烯復合材料拉伸強度的預測模型。為研究復合材料的斷裂機理，進行拉伸試驗，觀察斷口形貌，然后選擇Duva-Curtin-Wadley模型作為纖維斷裂判據，將其納入等效夾雜模型，結合Mori-Tanaka理論預測老化行為與失效情況，該方法雖然可對拉伸強度進行預測，但預測精度不佳。文獻［4］中通過對力學參數進行標定實驗獲得75組有效數據，由此構建了基于小樣本數據的傳統多元回歸方程、典型前饋式及反饋式神經網絡等不同預測模型，對模型的不同擬合效果和預測精度進行分析，再選用遺傳算法對最優的預測模型進行優化，以此實現對材料拉伸強度的預測。該方法雖然試驗成本較低，運算復雜度不高，但由于它是以膠脂為研究對象，在對碳纖維紙的拉伸強度進行預測時仍然存在預測精度較低的問題。

基于前人研究經驗，本文基于多元非線性數學模型構建一種預測模型，并將它應用到碳纖維紙拉伸強度預測當中。

1 基于多元非線性數學模型的強度預測模型構建

碳纖維紙的功能是保護膜電極集合體并傳導電流［5］。其位置如圖1所示。

圖1 碳纖維紙在燃料電池中的位置示意圖

碳纖維紙的獨特作用對其性能有著極高的要求，高抗拉強度就是其中之一［6］。為明確碳纖維紙的使用壽命，確定其失效機理，本文基于多元非線性數學模型建立一個預測模型，對碳纖維紙拉伸強度進行預測。首先篩選碳纖維紙拉伸強度的影響因素，而后基于多元非線性數學模型建立影響因素與拉伸強度之間的關系模型［7］。

1.1 碳纖維紙拉伸強度影響因素篩選

多元非線性數學模型預測原理是以自變量的變化來推斷因變量的變化，因此建立預測模型的前提條件是確定模型的自變量，也就是篩選與之息息相關的影響因素。目前影響因素篩選方法主要有兩種，一是GM（1，1）模型法，二是主成分分析法［8］。在這里，采用前一種進行影響因素篩選。下面對該方法篩選過程進行具體分析。

步驟1：收集資料，羅列可能對碳纖維紙拉伸強度產生影響的因素。這一環節羅列的影響因素越全面越好［9］。

步驟2：對羅列出來的影響因素進行整理，并重新排列組合。

步驟3：建立參考數列，即所有比較數列的對比標準，其形式如下：

式中，m為指標的個數。

步驟4：建立比較數列，它是由實際選出的所有影響因素構成，其形式如下：

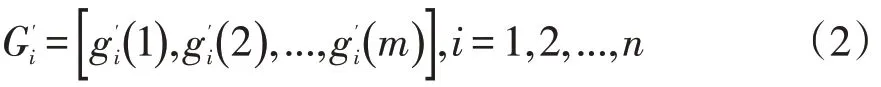
步驟5：按照公式（3）對所有影響因素進行無量綱化處理。

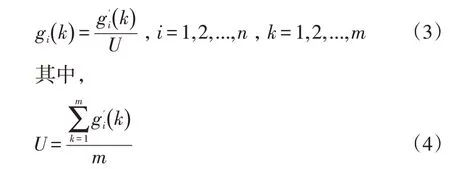
步驟6：計算比較數列與參考數列中各個影響因素的差值P，并進行絕對化處理［10］。公式如下：

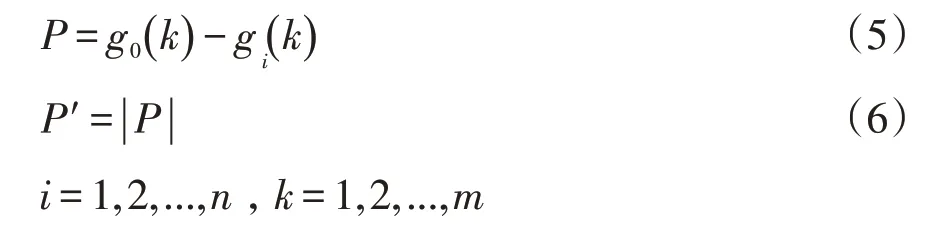
式中，P′為絕對差值，n為影響因素的數量。

步驟7：從計算出來的P′值中選出最大值p′max和最小值p′min。

步驟8：按照公式（7）計算各個影響因素的關聯系數ζi(k)，數學表達式如下：

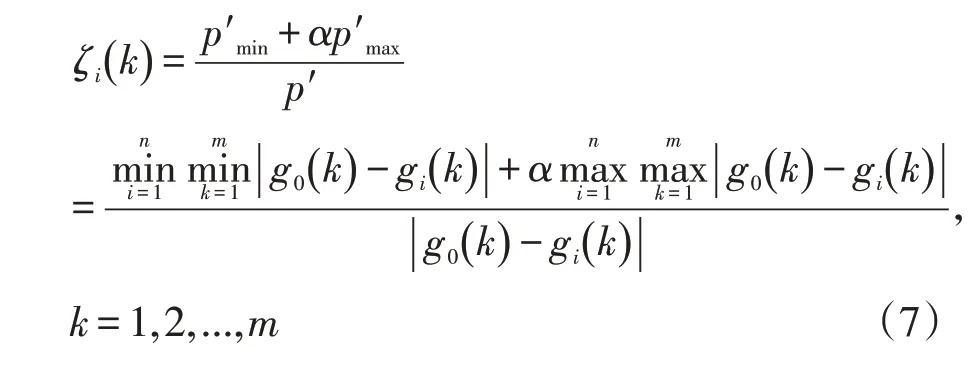
其中，α為分辨系數，0<α<1，一般情況下，取中間值0.5。

步驟9：將關聯系數集中為一個值，也就是計算數列關聯度β0i。計算公式如下：

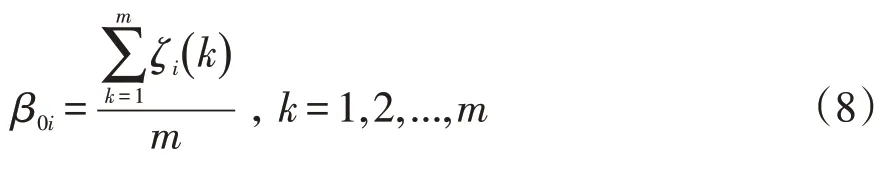
步驟10：關聯度排序，選取前n個影響因素作為影響碳纖維紙拉伸強度的主要因素。

1.2 強度預測模型構建

預測是指以一些已知數據來推斷未知數據的過程。本研究以已知的碳纖維紙拉伸強度影響因素來預測碳纖維紙拉伸強度這一因變量數值發生變化的情況。二者具有很強的關聯性，因此在這里引入多元非線性數學模型來構建二者之間的關聯預測模型［11］。下面進行具體分析。

多元非線性數學模型一般形式如下［12］：

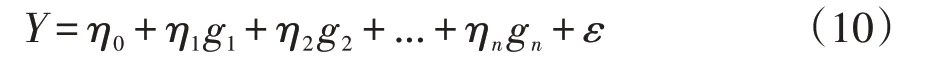
式中，η0,η1,...,ηn是n+1個待估參數；η0稱為回歸常數；η1,...,ηn稱為回歸系數；Y為因變量（碳纖維紙拉伸強度），g1,g2,...,g n為自變量（影響因素）；ε為隨機誤差。

（1）若給出了式中各個待估參數η0,η1,...,ηn的明確數值，記為，而ε則不再具有意義，因此公式（10）寫為

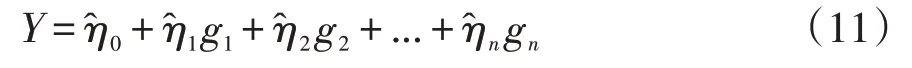
上述公式則不再稱為多元非線性數學模型，而是稱為多元經驗回歸模型。

（2）若給定一組自變量（影響因素）g1,g2,...,g n，則可以得到一個Y值，記為，?就是Y的一個預測值。這時隨機誤差ε常常假定為

式中，e為常數。

（3）若已獲得N組觀測數據(gi1,g i2,...,gin;Y i)，i=1,2,...,n，則公式（10）寫為

那么多元非線性數學模型就可以寫成如下的形式：

式中，G T為G的轉置。

2 碳纖維紙拉伸強度多元非線性預測模型應用分析

為檢驗多元非線性預測模型在碳纖維紙拉伸強度預測中的應用效果，通過實驗的方式來獲取N組碳纖維紙拉伸強度影響因素數據，然后以此為依據進行未來變化趨勢預測，檢驗模型的預測準確性［14］。

2.1 研究對象選擇

本文選擇的研究對象為一種高性能碳纖維紙TGP-H-060，該碳纖維基本參數如表1所示。

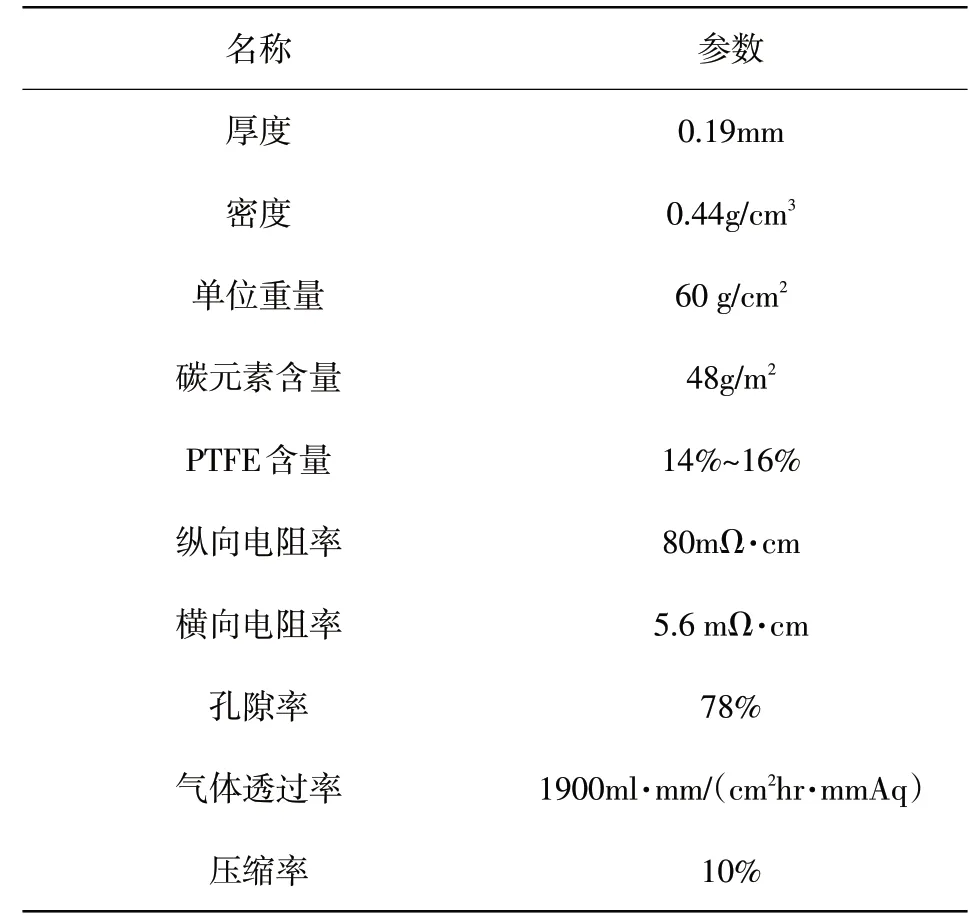
表1 TGP-H-060高性能碳纖維紙基本參數

2.2 影響因素篩選結果

結合TGP-H-060高性能碳纖維紙生產工藝以及生產環境，利用1.1的方法篩選對其拉伸強度有著明顯影響作用的因素，最終篩選出關聯度大于3的影響因素作為關鍵因素，結果如表2所示。

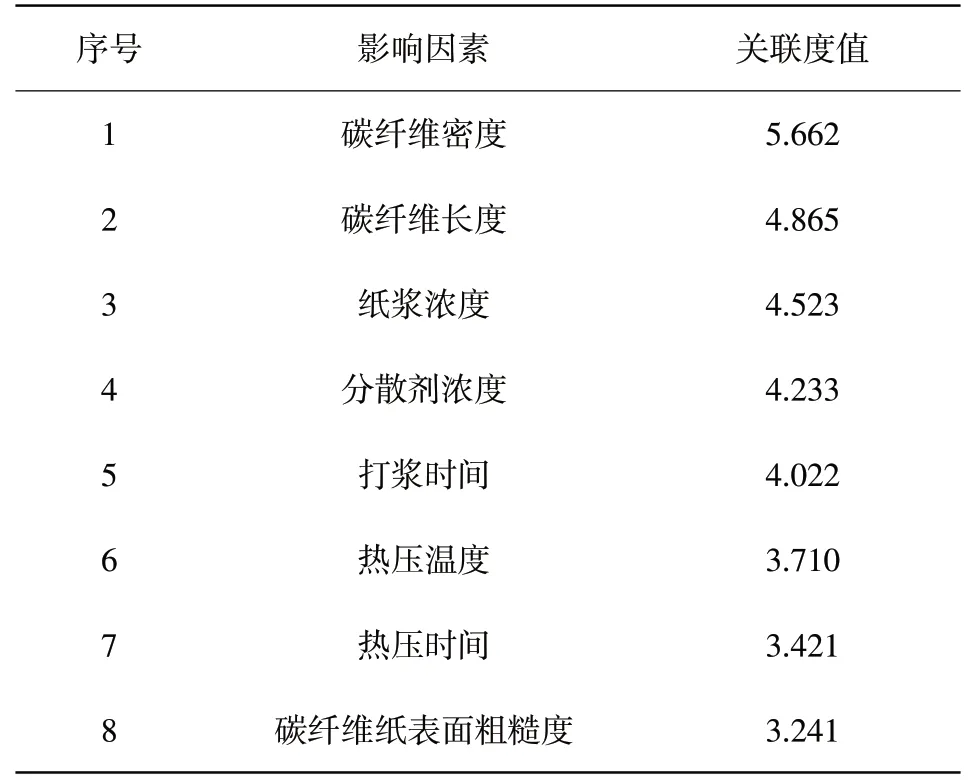
表2 TGP-H-060高性能碳纖維紙影響因素表

2.3 碳纖維紙拉伸強度測試設備

選取PY-H801電子拉力試驗機來測試紙張在恒速拉伸條件下的拉伸強度變化情況［15］。PY-H801電子拉力試驗機基本技術參數如表3所示。

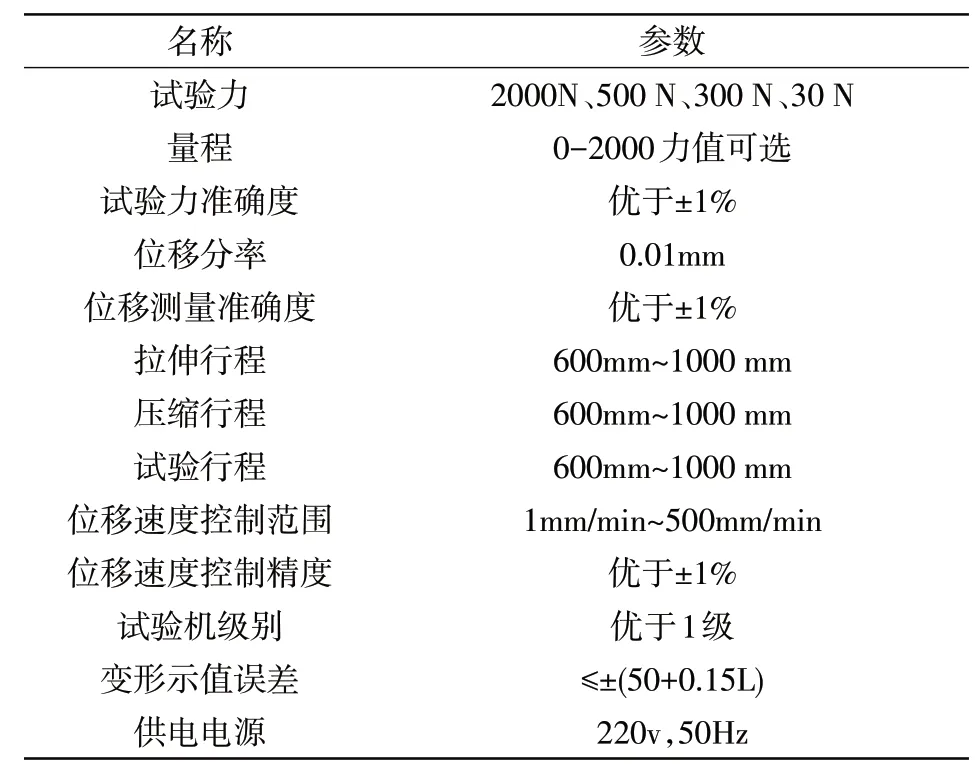
表3 PY-H801電子拉力試驗機基本技術參數

2.4 碳纖維紙拉伸試驗環境

將TGP-H-060高性能碳纖維紙裁剪成長度250mm、寬度15mm的試樣，將試樣放置到PY-H801電子拉力試驗機上，隨后向相反方向做拉力運動，采集這一過程中的力值和位移，以此計算拉伸強度值，如圖2所示［16］。

圖2 碳纖維紙拉伸實驗示意圖

2.5 觀測數據集

PY-H801電子拉力試驗機工作下，獲取得到10組影響因素值和碳纖維紙拉伸強度值，如表4所示。

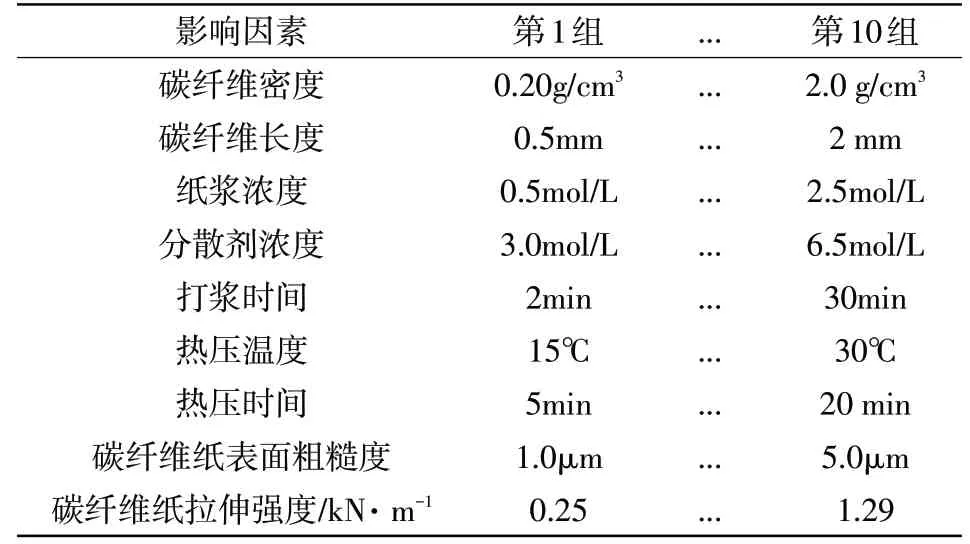
表4 觀測數據集

2.6 參數η0,η1,...,ηn估算與檢驗

以得到的前7組觀測數據為已知數據，輸入到式（11）當中，利用最小二乘法來計算模型當中的η0,η1,...,ηn值，并進行假設檢驗，結果如表5所示。

表5 回歸系數及其模型檢驗結果

根據表5，建立碳纖維紙拉伸強度預測模型如下：

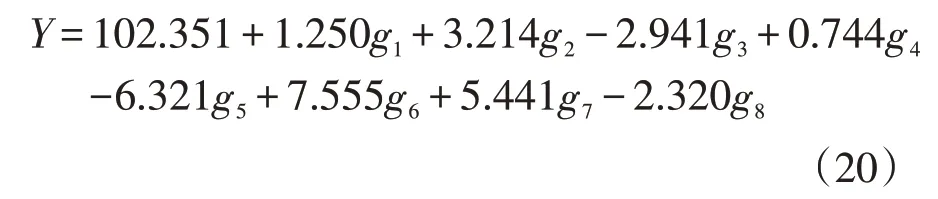
2.7 估測準確性檢驗

以表4后3組數據中的影響因素為準，利用公式（20）預測相應的碳纖維紙拉伸強度值，并與實際值進行對比，結果如表6所示。

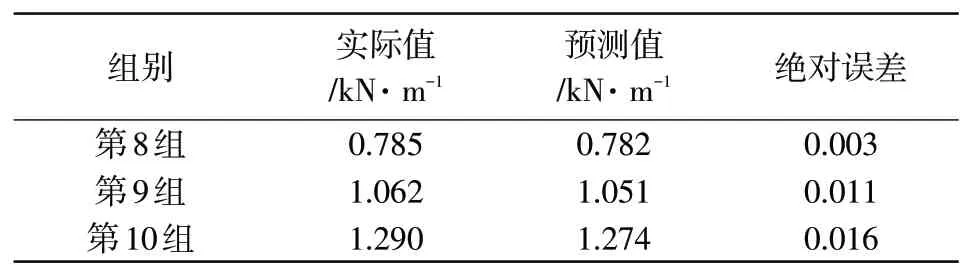
表6 估測準確性檢驗結果

從表6中可以看出，利用所構建的基于多元非線性數學模型的預測模型對碳纖維紙拉伸強度值進行預測，所得預測值與實際值之間的誤差小于1 kN·m-1，說明該模型的預測準確性較高，具有廣泛的應用前景。

3 結語

本文基于多元非線性數學模型構建碳纖維紙拉伸強度預測模型，并進行應用分析，檢驗模型的預測精度。經過應用檢測，模型預測準確性較高，其預測值與實際相比絕對誤差小于1 kN·m-1，證明所提方法預測值較為準確，具有廣泛的應用前景。雖然本文有效提升了預測精度，但仍存在一定不足，未來將繼續提升其預測精度。